Pdf: Tömörségi fok átszámítása az egyszerűsített- és módosított Proctor-vizsgálatok között
Bevezető, előzmények
A tömörség a legfontosabb minőségi jellemző a teherbírás mellett a mélyépítésben. A tömörség esetében hagyományosan a mért helyi nedves sűrűségből a víztartalom ismeretében számítjuk a száraz sűrűséget, majd ezt viszonyítjuk egy kiválasztott viszonyítási sűrűséghez, százalékban megadva.
A viszonyítási sűrűség meghatározására \((\rho_{dmax})\) Magyarországon a módosított Proctor vizsgálat, de például Németországban több előírásban az egyszerűsített Proctor vizsgálat szerepel. Az alkalmazott tömörségmérések általában közvetett módon, a sűrűség mérésén alapulnak, mint amilyen a homok-kitöltéses, a víztérfogat-méréses, vagy az izotópos sűrűségmérés. Újabban más viszonyítási sűrűségek is ismeretesek és szabványosak lettek, mint a vibrosajtolásos, vibrokalapácsos, vagy vibroasztalos szabványos európai vizsgálati módszerek. Ezek összefüggése a módosított, vagy egyszerűsített Proctor vizsgálatokkal még nem ismeretes, de modellhatásuk jelentősen eltér a laboratóriumi döngölős tömörítéstől.
A dinamikus tömörségmérés elmélete nem a viszonyítási sűrűséget használja fel, hanem a Proctor-görbe normalizált (\(\rho_{dmax}\)-szal elosztott) alakját alkalmazza, mint nedvesség korrekciós együtthatót. Az anyag (talaj) vízérzékenységi jellemzőjét a görbület tükrözi (nem a \(\rho_{dmax}\)), ez a dinamikus tömörségmérés egyik gyakorlati előnye.
A dinamikus tömörségmérés 10-18 ejtés süllyedési amplitúdójával jellemzett, azaz a térfogatváltozás mérésén alapuló vizsgálati módszer, melynél a Proctor-tömörítési munkának megfelelő ütéssorozattal hajtjuk végre – az adott helyszíni víztartalom mellett – a tömörítést. A dinamikus tömörségi fok (Trd%) a helyszíni relatív tömörség (TrE) és a nedvességkorrekciós tényező (Trw) szorzata, mely az adott nedvességtartalmú réteg helyszíni relatív tömörségi fokát az optimális víztartalom mellett létrehozható legnagyobb tömörségre átszámítva adja meg, így azonos a tömörségi fok az egyéb módon mért tömörségi fokkal.
Magyarországon a hatályos ÚT 2-1.222 „Utak és autópályák létesítésének általános geotechnikai szabályai” Műszaki előírás 4.5. pontja szabályozza a földművek építésének minőség-ellenőrzését. Az alkalmazható tömörségmérési módszerek lehetnek (4.5.1.2.pont), a kiszúró-hengeres, üregkitöltéses, izotópos, a B&C dinamikus ejtősúlyos, penetrométeres, a statikus tárcsás dinamikus modulus, FDVK vagy CCC teljes felületű gyorsulásmérős módszerek. Ezek közül összefüggések alapján lehet következtetni a tömörségi fokra. A viszonyítási sűrűséget alkalmazzuk a kiszúróhengeres, üregkitöltéses, vagy az izotópos módszerrel meghatározott terepi száraz sűrűségek értékeléséhez.
Magyarországon a töltéstest tömörségi követelményeinek értékeléséhez az ÚT 2-1.222 szerint viszonyítási sűrűség az MSZ-EN 13286-2 szerinti, módosított Proctor vizsgálattal maghatározott legnagyobb száraz térfogatsűrűség. Ha a tervező előírja, lehetséges a viszonyítási sűrűség maghatározása az MSZ EN 13 286-3 és MSZ EN 13 286-4, MSZ EN 13 286-5 szerinti dinamikus módszerekkel, de ehhez azonban a követelményeket (határértékeket) külön kellene meghatározni.
Fentiekből következik, hogy az MSZ 15846 (illetve a CWA15846 és az ÚT 2-2.124 ÚME) szerinti B&C dinamikus tömörség- és teherbírás vizsgálat az egyetlen, mely nem viszonyítással ad tömörségi fok eredményt. Ilyen számítás a többi módszerrel nem hajtható végre.
Jelen cikk bemutatja a B&C SP-LFWD (kistárcsás dinamikus tömörség- és teherbírás mérő) berendezéssel mért eredmények átszámításának módját, lehetőségeit, a Németországban alkalmazott egyszerűsített Proctor-vizsgálatnak megfelelő tömörségi fok értékeléshez, mely több tenderben, mint minősítési követelmény szerepel.
Tömöríthetőségi vizsgálatok
Módosított Proctor-vizsgálat
A módosított Proctor-vizsgálat (EN 13286-2 7.4. pont) lényege, hogy egy 10 cm átmérőjű, 12 cm (+5 cm feltét) magasságú hengerbe 5 rétegben 25-25 ütéssel talajmintát tömörítünk, 4,5 kg tömegű, 45 cm magasságból leejtett, 50 mm fejátmérőjű döngölőrúddal. A tömörítés után a feltét-gyűrűt levéve a felületet késsel lehúzzuk, majd a minta ismert térfogatából és tömegéből a nedves térfogatsűrűséget (\(\rho_{n}\)) meghatározzuk. A tömörített anyagból vett minták kiszárítása után meghatározzuk a víztartalmat, majd számítjuk a tömörítéssel készített minta száraz térfogatsűrűségét:
\[\rho_{d}=\frac{1}{1+\frac{w\%}{100}}*\rho_{n}\]
| ahol: | |
| \(\rho_{n}\) | testsűrűség (Mg/m3 vagy g/cm3 ); |
| \(w\%\) | minta víztartalma (%); |
| \(\rho_{d}\) | száraz sűrűség (Mg/m3 vagy g/cm3 ); |
Ezt a műveletet legalább három-öt különböző víztartalmú mintával megismételve, a kapott száraz térfogatsűrűség – víztartalom pontokat ábrázoljuk, ez a Proctor-görbe. Ennek maximuma a legnagyobb száraz térfogatsűrűség, melyhez az optimális tömörítési víztartalom tartozik. Javasolt számítani a telítési vonalakat is, hogy a helyszínen mért víztartalmat, a réteg telítettségét és ezzel a tömöríthetőségét e szempontból is értékelni lehessen. A módosított Proctor görbe maximuma és az ehhez tartozó optimális víztartalom (\(w_{opt-m}\) \(\rho_{dmax-n}\)) általában a talaj (szemcsés anyag) laboratóriumi alkalmassági vizsgálatának is része.
A Proctor munkavégzés mennyiségének számításakor a döngölő felületét kell(ene) figyelembe venni. A döngölés száma a kokilla területe és a döngölő területének hányadosa F1/F2=4 miatt átlagosan 5 réteg x 5 ütés)/4=125/4=31,25 átlagos tömörítő ütésszám /cilinder a Porctor-kokilla felületére vetítve. A munkavégzés értéke a fenti adatokkal számolva módosított a Proctor-vizsgálatnál:
\[W_{mPr}=4,5*0,45*9,81*31,25=621 J\]
Egyszerűsített Proctor-vizsgálat
Az egyszerűsített Proctor-vizsgálat során (EN 13286-2, 7.3.pont) 10 cm átmérőjű, 12 cm magasságú hengerbe 3 rétegben 25-25 ütéssel tömörítjük a talajmintát 2,5 kg tömegű, 30,5 cm magasságból leejtett, 50 mm fejátmérőjű döngölővel. A feltétgyűrűt levéve, a felületet késsel lehúzzuk, majd a minta ismert térfogatából és tömegéből a nedves térfogatsűrűséget meghatározzuk. A talajminta kiszárítása után számított víztartalom ismeretében meghatározzuk az egyszerűsített (standard) Proctor száraz térfogatsűrűségeket (ugyanúgy, mint a módosított Proctor-vizsgálatnál), legyen ez most jelölésében \(w_{opt-s}\), \(\rho_{dmax-s}\). A döngölés száma átlagosan a kokilla-terület/döngölő terület=4 miatt 75/4=18,75 tömörítő ütés/cilinder. A munkavégzés az egyszerűsített Proctor vizsgálatnál tehát (ha a döngölt felületet vesszük figyelembe):
\[w_{sPr}=2,5*0,305*9,81*18,75=140 J\]
A módosított és az egyszerűsített Proctor-vizsgálat legnagyobb száraz térfogatsűrűségének aránya változó 1,03-1,15 közötti érték, a tömörítési munkavégzés aránya pedig 4,4 azaz a módosított Proctor lényegesen nagyobb a tömörítési munkavégzést alkalmaz!
Egyéb tömöríthetőségi vizsgálatok
Újabban már nem csak a döngölős Proctor-vizsgálatok, hanem más, vibrációs tömörítési modellt alkalmazó vizsgálati módszerek alkalmazása is megengedett Európában a viszonyítási sűrűség meghatározására. Ezek előnyei jórészt a döngölés során létrejövő szemcseaprózódás elkerülésében jelentkeznek, másrészt a talajtömörítés valós modellhatáshoz (hengerek, béka) közelebb állnak.
Ilyen vizsgálati lehetőségek: EN 13286-3 Kötőanyag nélküli és hidraulikus kötőanyagú keverékek. 3. rész: A laboratóriumi viszonyítási térfogatsűrűség és a víztartalom vizsgálati módszerei. Vibrosajtolás szabályozott paraméterekkel, EN 13286-4 Kötőanyag nélküli és hidraulikus kötőanyagú keverékek. 4. rész: A laboratóriumi viszonyítási térfogatsűrűség és a víztartalom vizsgálati módszerei. Vibrokalapács, és EN 13286-5 Kötőanyag nélküli és hidraulikus kötőanyagú keverékek. 5. rész: A laboratóriumi viszonyítási térfogatsűrűség és a víztartalom vizsgálati módszerei. Vibroasztal.
Választott kiindulási adatok
Tanulmányunkhoz egy korábban már vizsgált iszapos homokliszt talaj vizsgálati eredményeit választottuk ki, melyre mind a módosított, mind az egyszerűsített Proctor vizsgálat egy időben készült el a Széchényi István Egyetem Geotechnikai laboratóriumában – így megbízhatósága nem megkérdőjelezhető (1. ábra).
A módosított Proctor-vizsgálat eredményei: \(w_{opt-m}\) = 11,0%, \(\rho_{dmax-m} = 1,93 g/cm^3\)
| \(w_{m}\) [%] | 6,0 | 9,3 | 13,0 | 14,8 | 17,1 |
| \(\rho_{dmax-m}\) [g/cm3] | 1,814 | 1,912 | 1,885 | 1,803 | 1,722 |
| \(T_{rg-m}\) [%] | 94,0 | 99,1 | 97,7 | 93,4 | 89,2 |
| \(T_{rw-m}\) | 0,940 | 0,990 | 0,977 | 0,934 | 0,892 |
Az egyszerűsített Proctor-vizsgálat eredményei: \(w_{opt-s}\) = 13,5%, \(\rho_{dmax-s} = 1,82 g/cm^3\)
| \(w_{s}\) [%] | 6,7 | 9,6 | 12,5 | 16,1 | 19,5 |
| \(\rho_{s}\) [g/cm3] | 1,640 | 1,726 | 1,811 | 1,773 | 1,670 |
| \(T_{rg-s}\) [%] | 90,1 | 94,8 | 99,5 | 97,4 | 91,8 |
| \(T_{rw-s}\) | 0,901 | 0,948 | 0,995 | 0,974 | 0,918 |
 |
A munkavégzés nagyságának hatása jól látható a Proctor-görbék elhelyezkedéséből. A száraz ágak közel párhuzamosak, a nedves ágak mindig a telítési vonalba illeszkedők kell legyenek. Az ábrából következik, hogy az intenzívebb tömörítés esetén az ehhez szükséges (azaz optimális) víztartalom mindig csökken.
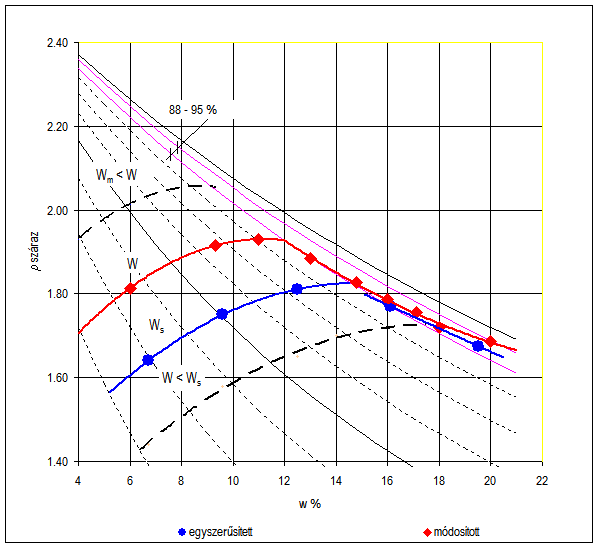 |
A víztartalom növelésével, a nedves ágon jól láthatóan egyre kisebb tömörség érhető el. A 3. ábra szerinti jelleg Dr. Kézdi Árpád Professzor szerint elemzett és leírt anyagviselkedés, melyből az is következik, hogy a jelenlegi két szint (egyszerűsített – módosított), bármikor tovább lenne bővíthető, annak csak a tömörítő gépek technikai fejlődése szab határt. Ha tehát a laboratóriumi tömöríthetőségi vizsgálatnál nagyobb munkavégzéssel tömörítünk a hengerrel, akkor a laboratóriumban megállapított optimális víztartalomnál kisebb lesz a valós helyszíni optimális víztartalom. A jelenleg alkalmazott, egyszerűsítettnek, vagy módosítottnak nevezett tömöríthetőségi munkavégzés tehát tulajdonképpen egy választás, vagy megállapodás kérdése.
Átszámítás az egyszerűsített és módosított Proctor szerinti tömörségi fokok között
Az SP-LFWD dinamikus tömörség- és teherbírás mérő berendezés a módosított Proctornak megfelelő munkavégzést alkalmaz, ezért az egyszerűsített Proctor-vizsgálatot alkalmazó országokban való alkalmazása ennek átszámítás nélkül korlátozott lenne.
 |
Nincs azonban akadálya annak, hogy ezt a számítást elvégezzük, így a B&C berendezés alkalmazását is lehetővé tegyük. Az adott talaj, szemcsés réteg anyagából az alkalmassági vizsgálat során minkét Proctor vizsgálatot elvégezték. A szokásos jellemzőket és a nedvességkorrekciós görbét ebből mindkettőre meghatározzuk. Az ábrákon és képletekben az egyszerűsített Proctor jellemzőknél „s” (simplefied), míg a módosítottnál „m” (modified) indexet alkalmaztuk.
Az átszámítási szorzót a két Proctor vizsgálatból kapott legnagyobb száraz sűrűségek aránya adja:
\[\beta=\frac{\rho_{dmax-s}}{\rho_{dmax-m}}\]
Az egyszerűsített Proctor munkavégzésének megfelelő tömörségi fok átszámításához (4. ábra), a módosított Proctor munkavégzéssel mért helyszíni relatív tömörségből számítjuk a módosított tömörségi fokot, majd a \(\beta\) tényezővel az egyszerűsített tömörségi fokra transzformáljuk azt. (Ezt oda-vissza is számíthatjuk, az ábrán külön színekkel jelöltük).
A példa szerint egyszerűsített Proctor szerinti 100% tömörség csak 94,3%-ot jelent a módosított Proctor szerinti skálán. Mivel a hengerlési munka megfelelőségének elbírálására a \(T_{rE}\%\) helyszíni relatív tömörségi fokot alkalmazzuk, azt is számítani kell. Ezt az egyszerűsített Proctor görbéből, \(T_{rw-s}\) nedvesség-korrekciós együtthatóval vesszük figyelembe.
Alakváltozás – tömörségi fok összefüggés az egyszerűsített Proctor vizsgálatnál
A dinamikus tömörségmérés elmélete a Proctor vizsgálatból elméleti úton levezethető. A \(G_{szaraz}= constans\) modellből számítjuk a tömörségi fok és az alakváltozás \(T_{rd}\% – {\Delta}{h} \) összefüggését, a meredekséget jellemző \(\Phi\) értékeit, mind a módosított (\(\Phi_{m}\)), mind az egyszerűsített (\(\Phi_{s}\)) Proctor-vizsgálat adataiból. Azt tapasztaltuk, hogy a \(\Phi\) értéke független attól, hogy módosított, vagy az egyszerűsített vizsgálatból számítjuk.
• a módosított Proctor-vizsgálat esetén: \(\Phi_{m}=0,366\) adódott (5. ábra).
 |
• az egyszerűsített Proctor-vizsgálat esetében \(\Phi_{s}=0,364\) adódott (6. ábra).
A módosított és egyszerűsített Proctor \(T_{rd}\%-{\Delta}{h}\) egyenese az azonos \(\Phi_{m}\) érték miatt párhuzamosak egymással és egymásba átszámíthatók.
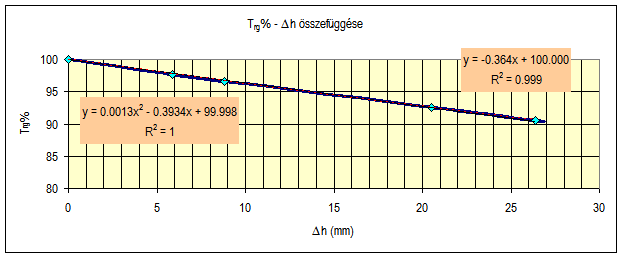 |
A tömörségi fok és az összenyomódás értékéből átlagolt összefüggés:
\(T_{rE}\%=-0,366*{\Delta}{h}+100\)
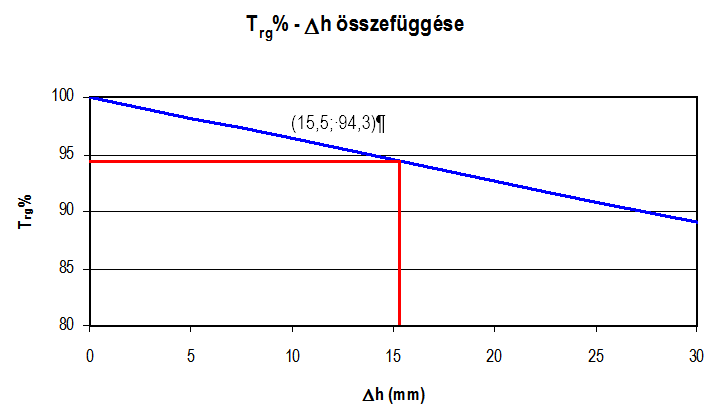 |
Az egyszerűsített Proctor-vizsgálatnál, a legnagyobb száraz sűrűségénél \(T_{rd-s}\%=100\%\), \(T_{rw-s}=1\), \(w_{opt-s}=13,5\%)\) a módosított Proctor szerinti tömörségi fokban kifejezve \(T_{rd-m}\%=\beta*100\), azaz 94,3%. A \(G_{szaraz}=constans\) modellből meghatározott összefüggés szerint az ehhez tartózó alakváltozás különbség számítható:
\[\Delta{h}= 1/\Phi *\Delta{T_{rd}}\%= 1/0,366*5,7=15,5mm\]
Megjegyzés: ez azt jelenti, hogy ha az egyszerűsített tömörségi fok 100%, akkor a módosított Proctor szerinti 100%-os tömörséghez a 25-30cm vastag rétegen még 15,5mm tömörödési alakváltozás szükséges, azaz az egyszerűsített Proctor tömörségi fok tovább tömöríthető. Emiatt a \(\beta\) szorzó kifejezhető a módosított Proctor így számított tömörségi fokából is (ha az egyszerűsített Proctor szerinti tömörségi fok 100%):
\[\beta=\frac{T_{rg-m}\%}{100\%}\]
Mintapélda
Helyszíni mérés eredménye
A jelen mintapélda szerint a helyszínen BC-vel mért relatív helyszíni dinamikus tömörségi fok (adott terepi víztartalom mellett) értéke \(T_{rE-m}\%=96,6\%\) iszapos homokon (siSa), wt=9,6% terepi víztartalom mellett, mely a Proctor görbe szerint \(T_{rw-m}= 0,996\) nedvességkorrekciós tényezőt jelent.
Módosított Proctornak megfelelő tömörségi fok számítása
Mérési eredmény a dinamikus tömörségi fokhoz a \(T_{rd-m}\%=T_{rE-m}\%*T_{rw-m}\) alap képlet alapján:
\[T_{rd-m}\%=96,6\%*0,996=96,2\%\]
Egyszerűsített Proctornak megfelelő tömörségi fok számítása
Ekkor a \(T_{rd-s}\%=1/\beta*T_{rd-m}=1/0,943*96,2\%=102,0\%\), az egyszerűsített Proctorral számított tömörség. Az egyszerűsített Proctor optimális víztartalma \(w_{opt-s}=13,5\%\). A természetes víztartalom ugyanaz \(w_{t}=9,6\%\), mely most \(T_{rw-s}=0,948\) nedvességkorrekciós tényezőt jelent.
Tudjuk, hogy a 100%-nak megfelelő módosított Proctor tömörítési munkához tartozó egyszerűsített Proctor-görbe legnagyobb lehetséges tömörsége 100%, a módosított Proctor szerinti értelmezésben 94,3%, az ennél nagyobb tömörségi fok érték a módosított Proctor szerinti skálán emiatt 100%-nál nagyobb egyszerűsített tömörségi fokot is eredményezhet. Ezért a német előírásokban előfordulhat a 100% feletti tömörségi fok előírása.
Egyszerűsített Proctornak megfelelő helyszíni relatív tömörségi fok számítása
Az egyszerűsített Proctorral számított tömörségből számíthatjuk az annak megfelelő helyszíni relatív egyszerűsített tömörségi fokot (On Site Simplified Relative Compaction Rate = OSSRCR), de természetesen a saját, egyszerűsített Proctorból meghatározott \(T_{rw}\)-s nedvességkorrekciós együtthatóval:
\[ T_{rE-s}=\frac{T_{rd-s}}{ T_{rw-s}}\]
A hengerlési munka megfelelőségét jellemző \(T_{rE-s}\) helyszíni relatív egyszerűsített tömörségi fok a mért \(w_{t}=9,6\%\)-nál az egyszerűsített Proctorból meghatározott \(T_{rw-s}\) görbe alapján \(T_{rw-s}= 0,948\), azaz
\[T_{rE-s}=\frac{102,0}{0,948}=107,6\%\]
azaz az adott víztartalomnál alkalmazott helyszíni relatív egyszerűsített tömörségi fok \(T_{rE-s}=108\%\) az egyszerűsített Proctornak megfelelő munkavégzéssel értelmezett esetben.
Helyszíni relatív tömörségi fok számítása különböző munkavégzéssel
A helyszínen, dinamikus módszerrel a módosított Proctor munkavégzésnek megfelelő helyszíni relatív tömörséget az adott természetes víztartalom mellett úgy határoztuk meg, hogy 10-18 ejtéssel tömörödési görbét hozunk létre, majd abból deformációs mutatót képezünk. A helyszíni mérést jellemző maradó alakváltozásból számított tömörséget, helyszíni relatív tömörségnek nevezzük és az adott víztartalom mellett elérhető tömörséget jellemző, legjobb esetben 100% érték.
A relatív tömörségi fok a következő képlettel határozható meg:
\[T_{rE-m}=100-\Phi*D_{m-m}\]
| ahol: | |
| \(D_{m-m}\) | a módosított Proctor munkavégzéssel számított deformációs együttható |
| \(\Phi\) | a meredeksége a Gsz=const modellből számított ΔVmm – Tr\% összefüggésnek (\(\Phi\) = 0,365 ± 0,025) |
A módosított Proctor szerinti munkavégzéskor a \(D_{m}\) értékét az alábbi súlyozott átlaggal, a summa maradó alakváltozásból számítjuk. A teljes alakváltozás \(h_{i}\) a rugalmas és maradó alakváltozások összege. Így a süllyedés negatív növekménye a következő módon számítható:
\[s_{i}=\frac{(h_{i}-h_{i+1})}{1}*i\cdots\]
ahol \(h_{i}-h_{i+1}>=0\), ha \(h_{i}-h_{i+1}<0\), akkor \(s_{i}=0\)
A rugalmas alakváltozás tehát kiesik a számításból. A süllyedés növekménye \(s_{i}\) az egyes ütéseknél egy numerikus derivált. Ezért ez a lépés értelmezhető úgy, hogy minden ejtésnél numerikus derivált. Az ejtésszám alapján visszafelé becsüljük az addigi teljes süllyedést. Ezt a súlyozott átlagot a deformációs együtthatónak \((Dm-m)\) nevezzük, a következő, általánosított módon számítható
\[D_{m-m},mm=\left[\sum_{i=1}^{i=6}{d_{i}}\dot{}\sum_{1}^{i}{SUM{\Delta}s_{i}}\right]\dot{}\frac{1}{17}\]
ahol
\[{SUM{\Delta_{s_{i}}}}={\Delta}s_{1}+{\Delta}s_{2}+\cdots +{\Delta}s_{i}\]
ahol a véglegesnek tekinthető alakváltozás rész \({\Delta}s_{1}+{\Delta}s_{2}+ … +{\Delta}s_{i}=\sum_{i=1}^{i=17}{\Delta}s_{i}\) , és \(d_{i}\) az ejtés száma \((i=1-18)\).
A \(h_{i}\) az ejtésekből létrejött rugalmas és maradó (teljes) alakváltozás, \(i = 1..18 \).
\(h_{1}\geq h_{2}\geq h_{3}\cdots h_{17}\geq h_{18}\)
Ha a \(SUM\Delta{si} =Si\) jelöljük, akkor
\[S_{1}=1*(h_{1}-h_{2})\]
\[S_{2}=2*(h_{1}-h_{2})+(h_{2}-h_{3})\]
\[S_{3}=3*(h_{1}-h_{2})+(h_{2}-h_{3})+(h_{3}-h_{4})\]
\[\cdots\]
\[S_{16}=16*(h_{1}-h_{2})+(h_{2}-h_{3})+\cdots +\cdots +(h_{16}-h_{17})\]
\[S_{17}=17*(h_{1}-h_{2})+(h_{2}-h_{3})+\cdots +\cdots +(h_{17}-h_{18})\]
Az egyszerűsített Proctor munkavégzésnek megfelelő helyszíni relatív tömörséget az előbb bemutatott átszámítási módszeren kívül úgy is meghatározhatnánk, hogy csak az annak megfelelő munkavégzést (ejtésszámot alkalmazzuk). A süllyedési amplitúdókból ekkor csak 6 ütéssel kellene a tömörödési görbét létrehozni, deformációs mutatót ebből számíthatjuk. A helyszíni „egyszerűsített Proctor-állapotot” létrehozó maradó alakváltozás göbéjét, a helyszíni relatív egyszerűsített tömörségnek nevezzük és az adott helyszíni víztartalom mellett elérhető legnagyobb tömörséget jellemző érték. Jelentős hátránya e módszernek, hogy ez esetben 100% feletti egyszerűsített Proctor tömörséget nem lehet mérni, ezért az előző, átszámításos módszer alkalmazása lehetséges. Az elmélet azonban az egyszerűsített Proctornak megfelelő helyszíni relatív tömörségi fok számítására is adaptálható:
\[T_{rE-s}=100-\Phi*D_{m-s}\]
ahol \(D_{m-s}\) a deformációs együttható. A teljes alakváltozás (mint előbb) itt is \(h_{i}\) a rugalmas és maradó alakváltozások összege. Így a süllyedés növekménye a következő módon számítható
\[s_{i}=\frac{(h_{i}-h_{i+1})}{1}*i \cdots \]
ahol \(h_{i}-h_{i+1}\geq {0}\), ha \(h_{i}-h_{i+1}<0\), akkor \(s_{i}=0\)
A rugalmas részt tehát kiküszöböltük a számításokban. A fenti súlyozott átlagot egyszerűsített Proctorhoz tartozó deformációs együtthatónak (\(D_{m-s}\)) nevezzük, a következő módon számítható
\[D_{m-s},mm=\left[\sum_{i=1}^{i=6}{d_{i}}\dot{}\sum_{1}^{i}{SUM{\Delta}s_{i}}\right]\dot{}\frac{1}{17}\]
A \(\Phi_{s}\) értéke empirikus módon meghatározott tényező, az egyszerűsített Proctor-vizsgálat Gsz=constans modellből számított \({\Delta}V_{mm}–T_{r{\rho}}\%\) egyenes lineáris együtthatója.
A \(h_{i}\) az ejtésekből létrejött rugalmas és maradó (teljes) alakváltozás, \(i = {1}\cdots {6}\).
\(h_{1}\geq h_{2}\geq h_{3} \cdots h_{17}\geq h_{18}\)
A dinamikus tömörségmérés elmélete tehát ugyanúgy alkalmas az egyszerűsített, mint a módosított Proctor munkavégzésnek megfelelő tömörségi fok számítására.
Azzal, hogy számos előírás az egyszerűsített Proctor alkalmazási területén nagyobb mint 100%, értelemszerűen és célszerűen az általános módon kell mérni a módosított Proctor szerinti munkavégzéssel, majd ezt átszámítani az egyszerűsítettre. Ily módon a 100% feletti tömörségi fokok is meghatározhatók. Ezek legnagyobb értéke legföljebb \(100*(1/\beta)\) lehet.
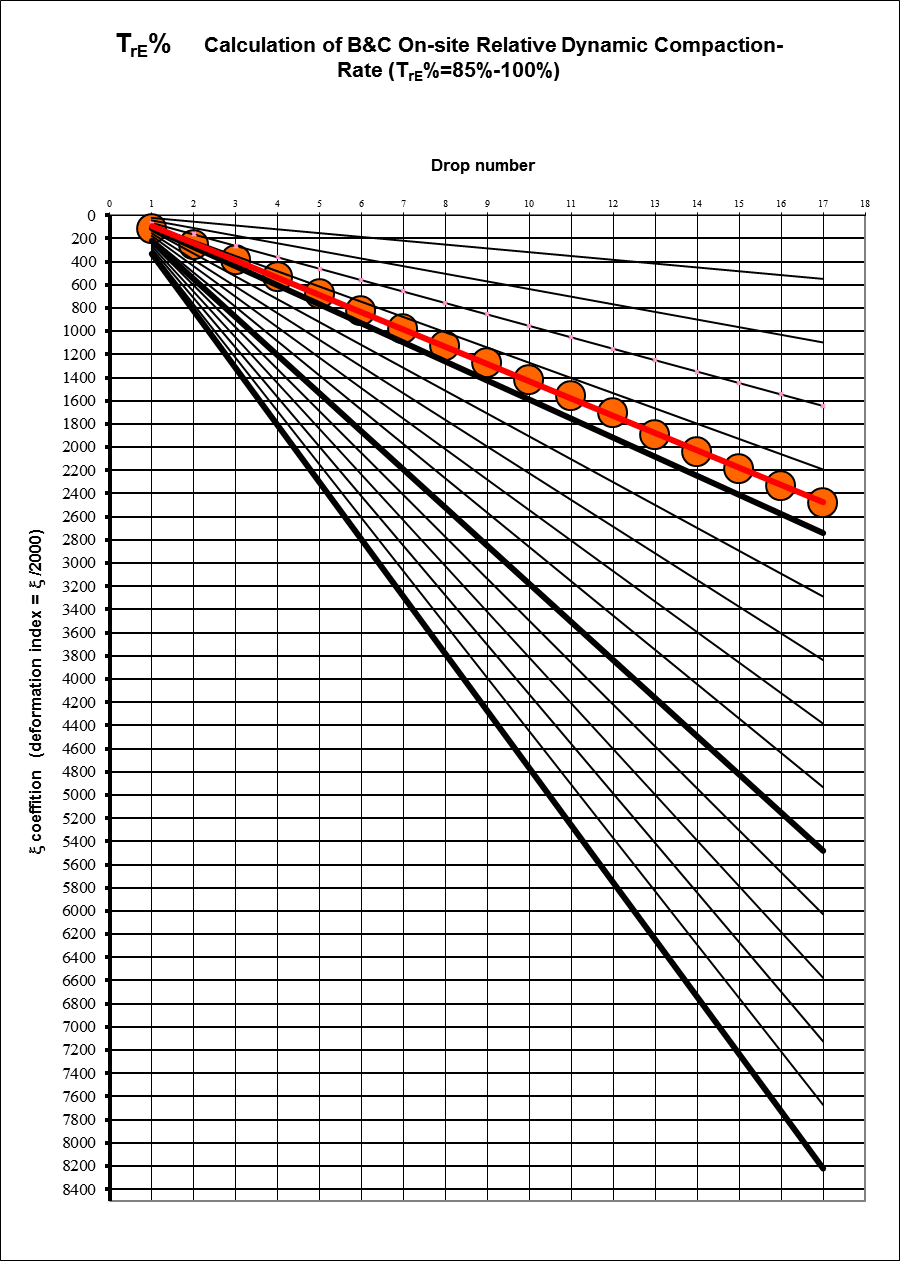
A \(\xi=2000/D_{m}\) bevezetésével a méréseket grafikusan is fel lehet dolgozni (8. ábra)
 |
Összefoglalás
A tömörség a legfontosabb minőségi jellemző a mélyépítésben a teherbírás mellett. A tömörségméréseknél viszonyítási sűrűségként a módosított Proctor vizsgálattal meghatározott legnagyobb száraz sűrűséget \((\rho_{dmax})\) használjuk, de Németországban még ma is alkalmazzák az egyszerűsített Proctorhoz történő viszonyítást. A módosított és az egyszerűsített Proctor legnagyobb száraz térfogatsűrűségének aránya jellemzően 1,03-1,15 közötti, a tömörítési munkavégzés aránya 4,4.
A különböző nagyságú munkavégzések jellegzetességei a Proctor-görbékből jól követhetők. A száraz ágak közel párhuzamosak, a nedves ágak a telítési vonalba illeszkedők. Egy kiválasztott munkavégzésnél intenzívebb tömörítés esetén tehát a szükséges víztartalom csökken, illetve a nedves ágon láthatóan a kisebb tömörítési munkával az optimális víztartalom növekedése törvényszerű, de kisebb tömörséget eredményez.
Kidolgoztuk azt a módszert, mellyel a B&C dinamikus SP-LFWD mérőberendezéssel az egyszerűsített Proctor szerinti helyszíni relatív tömörségi fok is mérhető. Ennek egyik lehetősége az átszámítás, a másik a kevesebb ejtésszám. A két módszer vizsgálata szerint előnyösebb annak választása, hogy a hagyományosan, a módosított Proctor szerinti munkavégzéssel meghatározott mérési eredményt átszámítjuk az egyszerűsített Proctorra, a \(\beta\) tényező alkalmazásával. A transzponálás mindig csak a \(T_{rd-m}\%\), \(w_{opt-m}\) értékénél a \(T_{rd-s}\%\), \(w_{opt-s}\) értékére történhet és az egyszerűsített Proctor helyszíni relatív tömörségét már a \(T_{rw-s}\) egyszerűsített Proctor nedvességkorrekciós együtthatójának figyelembe vételével kell számítani, a méréskor tapasztalt helyszíni víztartalomra.
A B&C dinamikus tömörség- és teherbírásmérő berendezés alkalmassá tehető mindkét tömörségi fok szerinti eredmény megadására. A szükséges ejtés-számok azonban arra figyelmeztetnek, hogy az egyszerűsített Proctor és a módosított Proctor szerinti munkavégzés közötti különbség igen nagy. A korszerű tömörítő gépek, hengerek teljesítményeit figyelembe véve a kivitelezés várható fejlődési iránya a magasabb tömörítési munkavégzés felé mutat.
Irodalomjegyzék
MSZ15846 Dinamikus tömörség- és teherbírásmérés SP-LFWD mérőeszközzel / Measuring Method for Dynamic Compactness & Bearing Capacity with SP-LFWD
CWA 15846 Measuring Method for Dynamic Compactness & Bearing Capacity with SP-LFWD
EN 13 286-2 Kötőanyag nélküli és hidraulikus kötőanyagú keverékek 2. Vizsgálati módszerek a laboratóriumi viszonyítási térfogatsűrűség és víztartalom meghatározására. Proctor-tömörítés (Mixtures without binding material and with hydraulic binding material 2. Test methods for the determination of the laboratory reference volume density and water content. Proctor-compaction)
EN 13 286-3 Kötőanyag nélküli és hidraulikus kötőanyagú keverékek 3. A laboratóriumi viszonyítási térfogatsűrűség és víztartalom vizsgálati módszerei. Vibrosajtolás szabályozott paraméterekkel
EN 13 286-4 Kötőanyag nélküli és hidraulikus kötőanyagú keverékek 4. A laboratóriumi viszonyítási térfogatsűrűség és víztartalom vizsgálati módszerei. Vibrokalapács
EN 13 286-5 Kötőanyag nélküli és hidraulikus kötőanyagú keverékek 5. A laboratóriumi viszonyítási térfogatsűrűség és víztartalom vizsgálati módszerei. Vibroasztal
MSZ 15320 Földművek tömörségének meghatározása radioizotópos módszerrel (Determination of the compactness of earthworks by radioisotopic method)
ÚT 2-2.124 Dinamikus tömörség- és teherbírásmérés kistárcsás könnyűejtősúlyos berendezéssel (Dynamic compactness and bearing capacity measurement with small-plate light falling deflectometer)
Dr Anna Petkovsek (2006): Report on usage of Andreas dynamic load bearing capacity and compactness deflectometer University of Ljubljana Katedra za mehaniko tal z laboratorijem. 2006 Ljubljana
Panarat (2006): Comparison of B&C LFWD and Sand Filling Method –Ramkhamhaeng University, Thailand
D. Adam – F. Kopf : Operational devices for compaction optimization and quality control (Continuous Compaction Control & Light Falling Weight Device)
Prof Dr Kézdi (Kalher) Árpád Talajmechanika I-II. TK. 1972. Budapest (Soil Mechanics Part I)
Prof Dr Nemesdy Ervin: Utak és Autópályák Pályaszerkezete TK 1971 Budapest Pavements of Road & Motorways
Prof Dr Nemesdy Ervin: Utak és autópályák tervezési alapjai TK 1974 Budapest
Dr Boromisza Tibor Talajmechanika, Alapozás I Szakközépiskolai Tankönyv
Dr Boromisza Tibor, Bertz Gy – Ébényi M.: Építőanyagok. TK 1974 az építőipari, az út- és vasútépítési , a vízügyi szakközépiskolák számára
Dr. Pusztai József – Dr. Imre Emőke – Dr. Lőrincz János – Subert István – Trang Quoc Phong: Nagyfelületű, dinamikus tömörségmérés kifejlesztése helyazonosítással és a tömörítőhengerek süllyedésének folyamatos helyszíni mérésével (Development of large-area, dynamic compactness measurement by site identification and the continuous on-site measurement of the settlement of compacting rollers). COLAS Report. 2007.
Dr Szendefy János – Vámos Máté: Egyszerűsített Proctor vizsgálati eredmények összehasonlítása, Műszaki Ellenőr 2014 nov-dec.
Subert I.: Egyszerűsített Proctor vizsgálati eredmények összehasonlítása – Hozzászólás Dr Szendefy János – Vámos Máté cikkéhez. Műszaki Ellenőr 39.sz. p.:42-55
Fáy M. – Király Á. – Subert I.: Egy földmű-tömörségi anomália feltárása és megoldása (Presentation and solution of an anomaly of earthwork density). Mélyépítéstudományi Szemle, 2006.
Fáy M. – Király Á. – Subert I.: Közúti forgalom igénybevételének modellezése új, dinamikus tömörség- és teherbírásméréssel (Modelling of the straining of public road traffic by the new, dynamic compactness and bearing capacity measurement). Városi Közlekedés, 2006.
Király Á. – Subert I.: Földmunkák minősítő vizsgálatainak hatékonysági kérdései Magyarországon (Efficiency issues of qualification tests used for earthworks, in Hungary)
Subert: ER-TRG01 Ellenőrzési rendszer próbatömörítések végrehajtására és értékelésére az M7 Zamárdi–Balatonszárszó szakaszán (Control system for the implementation and the evaluation of test compactions on the road section of M7 between Zamárdi and Balatonszárszó). Mérnöki Eljárási Utasítás. p. 10.
Subert I. – Phong T.Q.: Az izotópos és dinamikus tömörségi fok szórásanalízise 2007–2008. (Analysis of Standard deviation of the isotopic and the dynamic compactness rate)
Subert I. – Phong T.Q.: Proctor-vizsgálatok új értelmezési lehetőségei (Options for new interpretations of Proctor-tests). Mélyépítéstudományi Szemle, 2007.
Subert I. – Phong T.Q.: Sűrűségkorrekció alkalmazása dinamikus ejtősúlyos berendezéseknél, 2008. Andreas Kft www.andreas.hu
Subert I.: A dinamikus tömörség- és teherbírásmérés újabb paraméterei és a modulusok átszámíthatósági kérdései (Recent parameters of dynamic compactness and bearing capacity measurement and recalculation issues of moduluses). Közúti és Mélyépítési Szemle, 55. évf. 2005. 1. sz. p. 5.
Subert I.: B&C – egy hasznos társ (B&C – a useful partner). Magyar Építő Fórum, 2004/25. szám p. 36.
Subert I.: B&C dinamikus tömörségmérés (B&C dynamic compactness measurement). Mélyépítés, 2004 október–december pp. 38–39.
Subert I.: Dinamikus tömörségmérés a hazai autópályákon és városi helyreállításokon (Dynamic compactness measurement on Hungarian highways and urban reconstructions). Geotechnika Konferencia, Ráckeve. (2006. október 17–18.)
Subert I.: Dinamikus tömörségmérés aktuális kérdései. A dinamikus tömörségmérés újabb tapasztalatai (Recent issues of dynamic compactness measurement. New experiences of the dynamic compactness measurement). Geotechnika Konferencia, Ráckeve (2005. október 18–20.)
Subert I.: Új, környezetkímélő, gazdaságos mérőeszközök a közlekedésépítésben (New, environmental-friendly, economical measuring instruments in traffic building). Geotechnika Konferencia, Ráckeve (2004. október 26–27.)
Subert: Method for measuring Compactness-rate with New Dynamic LFWD. XIII. Danube–European Conference on Geotechnical Engineering Ljubljana, Slovenia, 2006.
