Pdf: Sűrűségkorrekció alkalmazása dinamikus ejtősúlyos berendezéseknél
Bevezető, előzmények
Az Infrastruktúra (vasút, közút, vízépítés, repülőtér) pályaszerkezetét megfelelő teljesítményképességű alapokra kell helyezni. Az alépítmény általában a földmű, beleértve esetleges javítórétegeit. Alkalmazni lehet és kell a másodlagos nyersanyagokat is egyre nagyobb arányban, melyek minőségellenőrzése mindeddig nem volt kellően biztosított. Jelen cikk bemutatja, hogy ezek a szélsőséges sűrűségű rétegek is minősíthetők, a dinamikus tömörség- és teherbírás mérési módszerét alkalmazva.
A dinamikus terhelés alkalmazása a terepi mérési módszereknél gyorsan terjed a világon. A könnyűejtősúlyos terhelési módszer alkalmazhatóságát növeli, hogy nem igényel ellensúlyt – mint a statikus teherbírás – és annak vizsgálathoz képest igen gyors. Lehetővé teszi a tényleges dinamikus forgalmi terheléssel azonos modellhatású mérést, egyben egy pontosabb és megbízhatóbb, reálisabb és gazdaságosabb minősítési mód alkalmazását, megnöveli a földművek és más szemcsés anyagrétegek minőségellenőrzésének hatékonyságát.
Magyarországon 2003-ban egy új, dinamikus módszerrel mérő berendezés kifejlesztése kezdődött, mely a két legfontosabb jellemző egyidejű mérésére alkalmas. A B&C SP-LFWD kistárcsás könnyű-ejtősúlyos berendezés egyrészt méri a dinamikus modulust, mint teherbírást, másrészt az ejtések hatására létrejött tömörödési görbéből a tömörségi fokot. A dinamikus tömörségi fok elméletét és mérésének módját az Andreas Kft dolgozta ki [22, 23, 24]. Az új módszer európai szabadalom lett és több díjat, elismerést kapott. 2008-ban elkészült a CEN-WA 15846 európai szabvány [1], mellyel a B&C dinamikus tömörség- és teherbírás mérő berendezés alkalmazása megnyílt Európa és a világ más országai előtt.
A B&C alkalmazása során nyert mérési tapasztalatok azonban rávilágítottak olyan a problémákra is, melyek eddig nem merültek fel, vagy nem voltak kezelhetők, ezek megoldását ugyanakkor a BC dinamikus teherbírás méréssel lehetségesnek tartottuk. A dinamikus tömörségmérési módszert Magyarországon már 28 laboratórium alkalmazza közel negyven mérőeszközzel. A mérőeszközöket a Közlekedéstudományi Intézet kalibrálja. A tapasztalatok külföldön is kedvezőek, az érdeklődés kiemelkedő. A B&C kistárcsás könnyűejtősúlyos berendezés a statikus teherbírás méréshez nagyon hasonló p=0,35 MPa tárcsa alatti terhelést alkalmaz, szemben más típusú nagytárcsás LFWD (Zorn, HMP) berendezésekkel, melyek a dinamikus modulus mérésére p=0,1 MPa tárcsa alatti terhelést használ [7-8].
Az új dinamikus tömörségmérési módszer alkalmazásáról, elemzéséről számos tudományos munka és tanulmány készült [16-18, 22, 25]. A mérőeszköz alkalmazási területének bővítéséhez szükségesnek és időszerűnek láttuk annak elemzését, hogy a talajoktól jelentősen különböző sűrűségű anyagok illetve a víztartalom, a réteg tömörsége milyen hatással van a mért tömörségi és teherbírási eredményekre.
Különösen fontos a vizsgálat a szélsőséges sűrűségű szemcsés anyagok, így a kohósalak, salakkő, pernye esetében, melyek mint másodlagos nyersanyagok alkalmazásra kell kerüljenek, ugyanakkor minősítésük (mérésük) nem megoldott. Ezek az anyagok közismerten nehezen, vagy egyáltalán nem minősíthetők a hagyományos tömörségmérési módszerekkel, különösen nem az izotópos tömörségmérési eljárással.
A dinamikus könnyűejtősúlyos teherbírás mérés alapelve
Az LFWD (Light Falling Weight Deflectometer) mérés elvét több európai szabvány és tanulmány részletezi [7-9]. Lényeges, hogy az ejtősúly 7070 N ± 2% terhelőerőt hoz létre a tárcsa erőátadó golyón. Típustól függően a tárcsa mérete D=300 mm, vagy a B&C esetében D=163 mm. Ebből adódóan a nagytárcsás készülékeknél 0,1 MPa, míg a kistárcsás B&C készüléknél 0,35 MPa tárcsa alatti terhelést jön létre a mért réteg felületén. A nagytárcsás készüléket a továbbiakban BP-LFWD-nek, a kistárcsásat SP-LFWD-nek nevezzük.
A tárcsa alatt mért alakváltozásból, süllyedésből számítjuk a Boussinesq-képlettel a dinamikus modulust. A nagytárcsás BP-LFWD fix Poisson-tényezőt és hajlékony tárcsa szorzót alkalmaz egy constans érték megadásával [6-7]:
\[C_{\mu} =22,5\]
\[E_{vd}=\frac{22,5}{s_{1a}}{\it (MPa)}\]
Az így kapott \(E_{vd}\) értékeket szokták \(E_{2}\)-re átszámítani – melyre különböző képletek ismeretesek -, de az összefüggés regressziós szorosságát nem ismerjük.
A magyar megoldás a B&C SP-LFWD, mely a mért anyagtípustól függően választható Poisson-tényezővel (\(\mu=0,3-0,4-0,5\)) és választható tárcsaszorzóval (\(c=2\), vagy \(\pi/2\)) dolgozik (emiatt \(C_{\mu}=valtozo\)).
\[E_{d}=\frac{(1-\mu^2)\dot{}c\dot{}p_{din}\dot{}r}{s_{a}}=\frac{C_{\mu}}{s_{a}}{\it\quad (1)}\]
Az így kapott Ed dinamikus modulus értékek hasonló mérési tartományt mutat, mint az E2 statikus teherbírás mérés, melyben lényeges szerepe lehet annak, hogy a statikus tárcsás mérésnél is p=0,3MPa tárcsa alatti végterheléssel mérünk.
Minden dinamikus terhelésű mérés az impulzus-törvényt használja fel arra, hogy a földmű, vagy pályaszerkezeti réteg felszínén terhelést hozzon létre. Ennek kapcsolatai, tömegei ismertek. Jelen tanulmány azt tűzte ki célul, hogy fenti kapcsolatok végigtekintésével, elemzésével tegyen megállapításokat a mért réteg sűrűségeltéréseinek lehetséges következményeire, az összefüggések feltárásával.
Az ejtősúly működése az impulzus-törvény alapján
Az „ejtősúly” kifejezés pontosítása érdekében elöljáróban szükséges hangsúlyozni, hogy milyen részeiről is beszélünk a készüléknek – általában. A vizsgálandó rétegre (talajra) helyezett tárcsára ejtjük le a súlyt, de oly módon, hogy azt egy ejtő-rúd megvezeti. A központosító golyóra ható impulzus tehát már a vezetőrúd és az ejtősúly együttes tömegéből származik, azaz más sebességgel mozog már, mint az ejtősúly maga a szabadesésben. Az erőhatás felépülése és lecsengése a teherátadó-központosító golyó előtt egy közbenső rugóval van szabályozva, melynek időszükséglete 18 msec-ban szabályozott mind a nagytárcsás BP-LFWD, mind a kistárcsás SP-LFWD típusú készülékeknél [1-3, 5-8].
A terhelőtárcsában elhelyezett gyorsulásmérő és a 0,001 sec pontosságú kvarcóra segítségével a mért időből és a tárcsa mért gyorsulásából számítható a megtett út, mint süllyedési amplitúdó. Ez a mutató mind a rugalmas, mind a maradó alakváltozást tartalmazza. Tárcsasebesség és benyomódás összefüggése nyilvánvaló, mivel az LFWD berendezéseknél az alakváltozást a tárcsa sebességéből és constans (18 msec) időből állapítjuk meg. Ha tehát a tárcsa sebességét ismerjük, akkor a tömeg és sebesség szorzatából az impulzus számítható.
A kioldókar meghúzása után a leeső súly tömege (kalibrálástól függően) 65-75 cm távolságú szabadesés után ütődik a csillapító rugó erőátadó szerkezetének. A központosító golyóra átadódó impulzus a tömegből, valamint a csökkent sebesség figyelembevételével számítható. Bár ejtősúly alatt a jelenlegi szabványok jellemzően a leeső súly tömegét értik (feltehetően ez egyértelmű), mégis a súly és a rúd + rugó együttes tömege képezi az impulzust a teherátadó golyón együttesen (Zorn, HMP és B&C), tehát az előírt 7070 N ± 2% nagyságú terhelés így alakul ki. Az impulzustörvény alapján a tömeg és sebesség szorzata állandó \((I=m\dot{}v)\).
Ha a kismértékű rúdsúrlódástól eltekintünk, akkor az impulzus sorozat egyszerű és könnyen áttekinthető.
| Készülék
Tömeg [kg] |
Zorn D=300 | B&C D=163 |
| Ejtősúly tömege | 11,0 | 10,4 |
| Ejtősúly + vezetőrúd tömege | 15,4 | 15,4 |
| Terhelő tárcsa tömege | 15,2 | 14,8 |
Ha az erőátadó golyóra jutó ejtősúly + vezetőrúd és a terhelőtárcsa tömege (1. táblázat) egyenlő, akkor a tárcsa sebessége azonos, ha eltérő, akkor a tömeggel fordítottan arányosan változik meg a sebesség. A tárcsa süllyedési sebességét a B&C dinamikus tömörség- és teherbírás mérő berendezés is gyorsulásmérővel méri és rögzíti. A készülék adattárolójában ezek a tárcsasebesség adatok tárolódnak, így utólag is rendelkezésre állnak. Innen származó sebességadatokból és a tárcsatömegből tehát mindenkor pontosan számítható az alkalmazott (tényleges) impulzus nagysága.
Talajra, szemcsés rétegre átadódó impulzus
Az impulzus végső oldala a mért anyagréteg, talaj, mely a tárcsa által átadott impulzus miatt tömörödik, lefelé mozdul. A talaj rugalmasságától függően, de a deformációra fordított energiával lecsökkentve, egy visszapattanást indít el a tárcsa felé. Az energia egy részét a maradó alakváltozás felemészti, ez az oka annak, hogy a visszapattanás sohasem éri el a végtelen merev modulusra jellemző \(h=v^{2}/2g\) értékét. Ehhez képest mért magasság-különbség azonban arányos az elnyelt energiával, az pedig a tárcsa alatti süllyedéssel.
A tárcsa alatti deformáció térfogatcsökkenést, sűrűség növekedést okoz. A tárcsa alatti terület és a hatásmélysége konstans, mely által meghatározott térfogatot tekinthetjük mértékadónak. Ennek tömege az, amit az impulzustörvény figyelembe vehet.
Az impulzustörvényben figyelembe vehető talajsűrűség a B&C mérési elméletéből könnyen számítható. A sűrűség egyenesen arányos a tömörséggel (minél kisebb a tömörség annál kisebb a sűrűség) és egyenesen arányos a víztartalommal (minél magasabb a nedvesség, annál nagyobb a sűrűség). Általánosságban tehát a mérés időpontjában a talaj sűrűsége a tárcsa alatt:
\[\rho_{n}={\rho}_{Pr}\frac{T_{rE}\%}{100}\dot{}\left(1+\frac{w_{\%}}{100}\right){\it\quad (2)}\]
| ahol: | |
| w% | a víztartalom a méréskor |
| ρPr | a Proctor-vizsgálat szerinti legnagyobb száraz sűrűség az EN 13282/2-7.4.pont szerint |
| TrE% | a mért réteg helyszíni relatív tömörsége az adott víztartalom mellett |
Mivel az altalaj különböző fajtájú és víztartalma is változó lehet, a visszapattanás (egyben a tárcsa alatt mért alakváltozás) értékei is ettől függőek. A mért süllyedési amplitúdó tehát tartalmazza ezek hatásait.
A fő kérdés, hogy a teherbírásra és a tömörségre vonatkozó minősítő határértéket ennek a mért értéknek kell-e teljesíteni, vagy a mért értéknek „anyagtól, víztartalomtól függetlenül” kellene teljesülnie. Nyilvánvalóan előnyös lenne egy általános minősítő határértékeket megadni (jelenleg alkalmazott is általános) és nem anyagfüggő módon kell kezelni (mint például az e-UT 06.03.13 – ÚT 2-1.202 ÚME eltakarás előtti teherbírási modulusokra adott anyagfüggő tájékoztató határértékeit).
Ezt a gondolkodásmódot indokolja továbbá az is, miszerint a beépített talaj idővel az optimális víztartalma közelébe és 100%-os tömörség közelébe kerül. Ha az előírt határértékeket úgy tekintjük, mint ennek elérését, akkor az optimálistól eltérő víztartalom és a nem kellő tömörség miatt logikusan csak ennek megfelelő teherbírást lehet elérni.
Nyilvánvalóvá vált, hogy amit mérünk, az egy adott víztartalmat, tömörséget tükröző érték, ezért korrigálni kellene ahhoz, hogy mértékadó eredményt kapjunk, amit a megadott teherbírási határértékhez hasonlíthatunk. Szükséges tehát annak elemzése, hogy a sűrűség hatása a dinamikus modulusra, illetve a dinamikus tömörségi fokra mekkora és milyen hatása van e tényezőnek, illetve, hogy a mért modulust módon korrigálhatjuk ahhoz, hogy azt az előírt (általános) határértékkel összehasonlíthassuk.
Talajtömeg számítása a víztartalma és tömörsége figyelembevételével
A visszapattanást előidéző impulzus nagysága attól függő, hogy a működésbe vont talajrész tömege mekkora. Ennek hatását legjobban egy példában tudjuk bemutatni négy választott anyagon. Két jelentősen eltérő sűrűségű a pernye és a kohósalakkő, illetve két kissé eltérő sűrűségű anyagot is vizsgáltunk, egy homokos iszapot (saSi) és egy finom homokot (Fsa). Ez utóbbit egyben bázisnak, viszonyítási alapnak választottuk (2. táblázat), mint jellemzően gyakran előforduló hazai altalajt.
Viszonyítási alapnak, bázisnak választott finom homok módosított Proctor vizsgálati sűrűsége \(\rho_{pr}=1,65g/cm^3\), melyet földmű építésben még elfogadható töltésépítő anyagnak tekintünk. Az optimális víztartalom ennél az anyagnál \(w_{opt}=7\%\), ± 3% a beépítésre előírt intervallum. Nedves sűrűsége az optimális víztartalomnál \(1,65\dot{}1,07=1,77g/cm^3\), illetve az anyag sűrűsége 95% tömörségi állapotban \(0,95\dot{}1,65\dot{}1,07=1,68g/cm^3\). Általánosságban a mérés időpontjában a mért talaj sűrűsége a (2) képlet szerint számítható.
| Anyagtípus | rdmax | wopt% | wopt%-3% | wopt%+3% |
| Pernye (fly-ash) | 1,00 | 26 | 23 | 29 |
| bázis =finom homok (Fsa) | 1,65 | 7 | 4 | 10 |
| Iszapos homok (siSa) | 1,72 | 11 | 8 | 14 |
| Kohósalakkő (slag) | 1,92 | 6 | 3 | 9 |
Hasonlóan képeztük a sűrűségeket a 3. táblázatban valamennyi anyagra, a három víztartalom és négy tömörségi kategória esetén. Az anyagok kiindulásul választott adatait a 2. táblázatban összesítettük.
Mivel a hatásmélység sűrűségtől függetlenül azonosnak vehető, a példánkban 25 cm-es hatásmélységnek megfelelő térfogatot választottunk ki. Kisebb tömörségnél ennek tömege kisebb, ezért a visszapattanás alacsonyabb, a mért süllyedési amplitúdó pedig nagyobb. Ha a bázisra vetített (mértékadó) értékre vagyunk kíváncsiak, akkor ennek hatását számítani és a mért értéket korrigálni szükséges. Ugyanez a logika vonatkozik a víztartalom hatásának számítására is.
Ha határértéket szabtunk a dinamikus modulusnak, akkor nem arra gondoltunk, hogy a víztartalom hatásától az függő lehet, vagy a tömörségtől kellene függővé tegyük. Ezzel azt is kimondtuk, hogy a határérték bizony más-más talajon nem ugyanazt a jellemzőt (és viselkedést) takarja.
| Trd (85-90-95) és w(opt, -3%, +3%) sűrűségek számítása | |||||||||||
| TrE%=85 | TrE%=90 | TrE%=95 | TrE%=100 | ||||||||
| 1,07 | 1,05 | 1,10 | 1,13 | 1,11 | 1,16 | 1,20 | 1,17 | 1,23 | 1,26 | 1,23 | 1,29 |
| 1,50 | 1,46 | 1,54 | 1,59 | 1,54 | 1,63 | 1,68 | 1,63 | 1,72 | 1,77 | 1,72 | 1,82 |
| 1,62 | 1,58 | 1,67 | 1,72 | 1,67 | 1,76 | 1,81 | 1,76 | 1,86 | 1,91 | 1,86 | 1,96 |
| 1,73 | 1,68 | 1,78 | 1,83 | 1,78 | 1,88 | 1,93 | 1,88 | 1,99 | 2,04 | 1,98 | 2,09 |
| wopt% | -3% | +3% | wopt% | -3% | +3% | wopt% | -3% | +3% | wopt% | -3% | +3% |
| Sűrűségarányok | |||||||||||
| TrE%=85 | TrE%=90 | TrE%=95 | TrE%=100 | ||||||||
| 0,61 | 0,59 | 0,62 | 0,64 | 0,63 | 0,66 | 0,68 | 0,66 | 0,69 | 0,71 | 0,70 | 0,73 |
| 0,85 | 0,83 | 0,87 | 0,90 | 0,87 | 0,93 | 0,95 | 0,92 | 0,98 | 1,00 | 0,97 | 1,03 |
| 0,92 | 0,89 | 0,94 | 0,97 | 0,95 | 1,00 | 1,03 | 1,00 | 1,06 | 1,08 | 1,05 | 1,11 |
| 0,98 | 0,95 | 1,01 | 1,04 | 1,01 | 1,07 | 1,10 | 1,06 | 1,13 | 1,15 | 1,12 | 1,19 |
| wopt% | -3% | +3% | wopt% | -3% | +3% | wopt% | -3% | +3% | wopt% | -3% | +3% |
| korrekciós tényező (Ed minősítő=Ed mért*korrekciós tényező) | |||||||||||
| 1,65 | 1,69 | 1,61 | 1,56 | 1,59 | 1,52 | 1,47 | 1,51 | 1,44 | 1,40 | 1,44 | 1,37 |
| 1,18 | 1,21 | 1,14 | 1,11 | 1,14 | 1,08 | 1,05 | 1,08 | 1,02 | 1,00 | 1,03 | 0,97 |
| 1,09 | 1,12 | 1,06 | 1,03 | 1,06 | 1,00 | 0,97 | 1,00 | 0,95 | 0,92 | 0,95 | 0,90 |
| 1,02 | 1,05 | 0,99 | 0,96 | 0,99 | 0,94 | 0,91 | 0,94 | 0,89 | 0,87 | 0,89 | 0,84 |
| wop% | -3% | +3% | wopt% | -3% | +3% | wopt% | -3% | +3% | wopt% | -3% | +3% |
Egy bázisnak tekintett és ehhez képest más sűrűségű talaj (anyag) tömegarányát elemezve megállapítható:
\[\frac{G_{1}}{G_{2}}=\frac{V_{1}\dot{}{\rho}_{1}}{ V_{2}\dot{}{\rho}_{2}}\]
mivel \[ V_{1}= V_{2}\] azonos ezért \[\frac{G_{1}}{G_{2}}=\frac{{\rho}_{1}}{{\rho}_{2}}\]
azaz a hatásmélységtől független a megállapításunk. Ugyanez a logikája a víztartalom változásának is:
\[\frac{G_{1}}{G_{2}}=\frac{V_{1}\dot{}{\rho}_{1}(1+w_{1})}{ V_{2}\dot{}{\rho}_{2}(1+w_{2})}\]
azaz \[\frac{G_{1}}{G_{2}}=\frac{{\rho}_{1}(1+w_{1})}{{\rho}_{2}(1+w_{2})}\] azaz a térfogat kiesik az aránypárból.
A sűrűségi és víztartalmi korrekció fentiekből:
\[\varsigma=\frac{{\rho}_{1}(1+w_{1})}{{\rho}_{2}(1+w_{2})}{\it\quad (3)}\]
Dinamikus modulus korrekciója, minősítő dinamikus modulus
A dinamikus modulus számítása (1) az (s) süllyedési amplitúdó mérése alapján történik. Ha a mért anyag sűrűsége változik, akkor a süllyedési amplitúdó is, azaz a dinamikus modulus is. A dinamikus modulus tehát a sűrűséggel arányos, ami azonban függ a talaj tömörségétől és a víztartalmától.
Az alkalmassági vizsgálatból ismerjük a talaj legnagyobb száraz Proctor sűrűségét és az optimális víztartalmát. Tudjuk továbbá a beépítésre, a víztartalomra előírt tűrést. A víztartalmat a helyszínen minden tömörségmérésnél mérni kell, így ezek az adatok rendelkezésre állnak. Ahol a CWA15846 szerinti SP-LFWD műszerrel mérjük a dinamikus teherbírást, ott mindig rendelkezésre állhat tömörségi adat is. A B&C berendezésnél minden dinamikus tömörségméréskor van mért adat a dinamikus teherbírásra is, mivel egy méréssorozatban mérjük a tömörséggel. 10 db (max 18) ejtésből számítjuk a tömörségi fokot, a 4-5-6 süllyedési amplitúdó átlagából a dinamikus modulust.
A 3. táblázatban számított korrekciós tényezőket alkalmazva bemutatjuk, hogy Ed=40MPa mérési eredmény a tömörség miatti, víztartalom miatti korrekciók után a következőképpen jellemezhető (4. táblázat), a vizsgálat tárgyát képező anyagokra (a sorok sorrendben pernye, finom homok, iszapos homok és kohósalak).
| Ed min minősítő, mértékadó érték: Ed mért = 40MPa* korrekciós tényező | Anyag | |||||||||||
| 65.9 | 67.5 | 64.4 | 62.3 | 63.8 | 60.8 | 59.0 | 60.4 | 57.6 | 56.0 | 57.4 | 54.7 | Pernye |
| 47.1 | 48.4 | 45.8 | 44.4 | 45.7 | 43.2 | 42.1 | 43.3 | 41.0 | 40.0 | 41.2 | 38.9 | H,Bázis |
| 43.5 | 44.7 | 42.4 | 41.1 | 42.2 | 40.0 | 38.9 | 40.0 | 37.9 | 37.0 | 38.0 | 36.0 | I-HL-H |
| 40.8 | 42.0 | 39.7 | 38.6 | 39.7 | 37.5 | 36.5 | 37.6 | 35.5 | 34.7 | 35.7 | 33.7 | K |
| wo | -3% | +3% | wopt% | -3% | +3% | wopt% | -3% | +3% | wopt% | -3% | +3% | w% |
| TrE%=85 | TrE%=90 | TrE%=95 | TrE%=100 | TrE% | ||||||||
A mért értékből számítottuk a százalékos arányokat is. Ezt úgy adjuk meg, mint jellemző terjedelmet a jelenleg vizsgált esetekre (mely a szélsőséges és a nem szélsőséges sűrűségi eltérésű anyagokra egyformán érvényes), az 5. táblázatban.
| Mind a négy vizsgált anyagra | Átlag | 100% |
| Min | 74% | |
| Max | 148% | |
| Szórás | 21% | |
| Bázis és iszapos homokra | Átlag | 100% |
| Min | 86% | |
| Max | 116% | |
| Szórás | 8% |
A dinamikus modulusra vonatkozó elemzésünk összefoglalásaként rögzíthető, hogy a vizsgált szélsőséges sűrűségű (de az építési gyakorlatban előforduló) anyagokat vizsgálva a dinamikus modulus sűrűség-korrekciós tényezője jelentősen megváltoztatja a modulus értékét, a korrekciós tényező terjedelme jelentős 1,69 és 0,84 közötti (!). Még kisebb sűrűségi eltérés és megengedett víztartalom tartomány mellett sem hanyagolható el a korrekció, mely -14%, +16% százalékos eltérést mutat a 85-100 % tömörségi tartományban, tehát az általános mérési esetekben. Fentiek alapján minden mért dinamikus modulust minden esetben korrigálni kellene ahhoz, hogy azt a határértékhez viszonyítsuk, mert az eltérés jelentős lehet. Korrekciója általánosan:
\[{\varsigma}_{E}=\frac{{\rho}_{1}(1+w_{1})}{{\rho}_{2}(1+w_{2})}\dot{}\frac{100}{T_{rE}\%}{\it\quad (4)}\]
Ha a dinamikus teherbírást pontosan kívánjuk meghatározni (pláne például összefüggést vizsgálni a statikus teherbírás \(E_{2}\) értékével), akkor korrekció nélkül a következtetések, összefüggések nem tekinthetők elfogadhatónak. Megállapításaink értelemszerűen adaptálhatók valamennyi dinamikus mérőeszközre, mint az FWD típusú (KUAB, Dynatest) mérőeszközökre. Ezek korrekciójával (a minősítő dinamikus modulus fogalmának bevezetésével) jelentős előrelépés tehető az összefüggések újravizsgálásával.
Kijelenthető tehát, hogy a dinamikus modulus pontos értéke csak a sűrűség (tömörségi fok, a víztartalom és a legnagyobb száraz Proctor sűrűség) ismeretében határozható meg.
A dinamikus tömörségi fok korrekciója
Az előző gondolatmenet alapján a mért süllyedési amplitúdót is lehet korrigálni, a víztartalom és sűrűség értékeinek változása miatt. Mivel azonban a dinamikus tömörségi fok számítása során a süllyedési amplitúdók különbségét (a maradó alakváltozást) vesszük figyelembe, a hatása is más. A víztartalom eltérése miatti korrekció tekintetében is más a helyzet, mivel a \(w_{opt}\) környezetében a \(T_{rw}\) értéke \(\left(\frac{\rho_{di}}{\rho_{dmax}}\right)\) alig változik.
A választott anyagokra elvégeztük a \(T_{rE\%}\) helyszíni relatív dinamikus tömörségi fokra vonatkozó elemzést, melyet a 6. táblázatban mutatunk be. Megállapítható, hogy a korrekciós szorzó kiemelhető a deformációs együttható képletből a \(D_{m}\) elé.
\[T_{rE\%}=100-\phi\dot{}\varsigma\dot{}D_{m}{\it\quad (5)}\]
és
\[T_{rd\%}\dot{}T_{rw}\]
ahol
\[D_{m}=\left[\sum_{i=1}^{i=17}{d_{i}}\dot{}\sum_{1}^{i}{SUM{\Delta}s}\right]\dot{}\frac{1}{17}\]
A választott anyagokból egy-egy adatsort választottunk a vizsgálat tárgyául, melynél megvizsgáltuk, hogy a víztartalom és sűrűség hatásait figyelembe vevő korrekciós együttható (3-as képlet) egy választott ζ=0,85-0,9-0,95-1,0-1,05-1,1-1,15 aránysoránál a számított helyszíni relatív tömörségi fok (TrE%) hogyan változik.
| ζ= | TrE% | 56. mérés | 62. mérés | ζ= | eltérés | 56. mérés | 62. mérés | |
| 0.85 | 95.8 | 92.0 | 90.3 | -0.15 | 0.70 | 1.40 | 1.70 | |
| 0.90 | 95.6 | 91.6 | 89.7 | -0.10 | 0.50 | 1.00 | 1.10 | |
| 0.95 | 95.3 | 91.1 | 89.2 | -0.05 | 0.20 | 0.50 | 0.60 | |
| 1.00 | 95.1 | 90.6 | 88.6 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 1.05 | 94.8 | 90.2 | 88.0 | 0.05 | -0.30 | -0.40 | -0.60 | |
| 1.10 | 94.6 | 89.7 | 87.4 | 0.10 | -0.50 | -0.90 | -1.20 | |
| 1.15 | 94.3 | 89.2 | 86.9 | 0.15 | -0.80 | -1.40 | -1.70 |
A 6. táblázat bemutatja a B&C berendezéssel 10-18 ejtéssel 25 mérési adatsor elaszticitás vizsgálatát. Az eredményeket úgy dolgoztuk fel, hogy a süllyedési amplitúdóknál a sűrűségkorrekciót is figyelembe vettük, a helyszíni relatív tömörségi fokot újra számítottuk, eltérését meghatároztuk. Minden korrekcióra számítottuk a 25 mérés helyszíni relatív tömörség fok értékeinek átlagát, illetve kiemeltük a 56.-os és 62.-es jelzésű mérést, melynél a helyszíni relatív tömörségi fok a legalacsonyabbra adódott, ezért a legérzékenyebb. Például a 25 mérés TrE% átlaga 95,1 %-ről 95,8 %-ra változik a 0,85 sűrűségkorrekciós tényezőnél. Mivel a tömörségi fokot egész számra kell kerekíteni megállapítható, hogy a dinamikus tömörségi foknál tapasztalt eltérés a hagyományos anyagoknál a sűrűségkorrekció miatt legföljebb 1 % körüli, azaz nem jelentős. Az 1. ábra mutatja a sűrűségkorrekció hatását az átlagos, valamint 56. és 62. kiemelt mérések helyszíni relatív tömörségi fokára.
Ezek lineárisak, meredekségük változó és az összefüggésük a következő:
– 25 mérés átlaga TrE%= -5 ζ + 100
– a kiemelt 56. mérésnél TrE%= -9,4 ζ + 100
– a kiemelt 62. mérésnél TrE%= -11,4 ζ + 100
 |
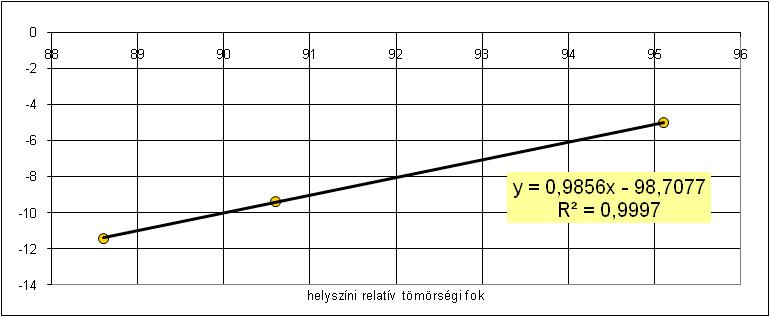
A mért helyszíni relatív tömörségi fok és a sűrűségkorrekció közötti összefüggés a meredeksége (m) tehát függ a relatív tömörségi foktól is (mely meghatározható). Az \((m)\) meredekség és a helyszíni relatív tömörségi fok közötti összefüggést megvizsgálva (2. ábra) a következőt kaptuk:
\[m=0,986\dot{}Tr_{E\%}-98,7\quad({R}^{2}=1,0){\it\quad (6)}\]
Fentiek szerint a sűrűség hatása hagyományos anyagoknál a relatív tömörségi fokra igen kis mértékű, de nagy pontossági igény esetén számítható. Jelentősége igazán a pernye anyagok építőipari alkalmazásánál van, mert sűrűsége igen alacsony.
Példaként bemutatjuk a H-TPA laboratórium által mért dinamikus tömörség- és teherbírás mérési eredményt az M35 autópálya 21+875 kmsz pernyetöltésén. A mért értékek Ed=18,9MPa, TrE%=91,7%, wt=38,3 % voltak. A nedves sűrűség 1,26 g/cm3, Proctor ρdmax=0,91 g/cm3 és wopt=26%, Trw=0,985. Megjegyzés: statikus teherbírás E2=37 MPa, Tt=1,6 és kiszúró hengeres tömörségi fok Trρ=98,3 % volt.
 |
Számítások
• sűrűségkorrekció 3-as képlettel ζ= (0,91 x 1,26)/(1,65 x 1,07)=1,147/1,766=0,649
• minősítő dinamikus tömörségi fok számítása:
m= (TrE% x 0,986)-98,7= -8,3 → TrE% minősítő = – 8,3 x 0,649 + 100=94,6%
Trw=0,985 → Trd% minősítő = Trw x TrE=0,985 x 94,6 = 93,2% > 90%
• minősítő dinamikus modulus
Ed minősítő = Ed x (1/ζ) x (100/Trd%)
Ed minősítő = 18,9 x (1/0,649)x(100/93,2)=18,9 x1,54 x1,07=31,1 MPa < 40 MPa
Mint látható, a sűrűségeltérések dinamikus tömörségi fokra gyakorolt hatása az impulzus-vizsgálat szerint kevésbé releváns, mint a teherbírásnál. A sűrűségnek tehát az általánosan használt anyagoknál nincs jelentős hatása a dinamikus tömörségi fokra. Ezt egyébként már tapasztaltuk a Proctor-vizsgálatok elemzésekor, amikor a Φ értékét vizsgáltuk, mind elméleti mind gyakorlati vonatkozásban. Pernye vizsgálata esetén azonban a mért helyszíni relatív tömörségi fokot korrigálni kell, mert egyedül ennek hatása lehet olyan jelentős, hogy a biztonság javára már nem elhanyagolható.
Összefoglalás
A nagytárcsás LFW berendezéssel a mért dinamikus modulusokra jellemzően nincs előírás a szabványban [6, 7, 8] a párhuzamos eredmények meghatározására, átlagképzésre, az eredmény egyetlen vizsgálat, ettől pedig az eredmény különösen érzékeny. A B&C SP-LFWD mérés ÚT2-2.124, MSZ15846 illetve CWA 15846 a mértékadó dinamikus modulus képzésére előírja, hogy egy méteren belül két mérést kell végezni, illetve azt átlagolni, ezért pontosabb eredményt ad [1, 2,5].
Minden dinamikus mérés az impulzus-törvényt használja fel arra, hogy a földmű felszínén terhelést hozzon létre. Ennek kapcsolatai, tömegei ismertek. Jelen tanulmány azt tűzte ki célul, hogy ezen kapcsolatok végigtekintésével, elemzésével tegyen megállapításokat a talaj sűrűségeltéréseinek következményeire, esetleges összefüggéseit feltárva. Szükségesnek láttuk annak elemzését, hogy a különböző sűrűségű anyagok illetve azonos anyagnál talajállapotok (víztartalom, tömörség) esetén, de különösen a szélsőséges esetekben mért dinamikus modulusnál milyen hatás, milyen kapcsolat mutatható ki, korrekció alkalmazása szükséges-e, illetve lehetséges-e. Különösen fontos megemlíteni e problémakörben a kohósalakot, salakkövet, pernyét, pernyés stabilizációt, meszes stabilizációt, melyek mint másodnyersanyagok (újrafelhasználás, inert anyagok), illetve mint stabilizálási technológiák melyek sűrűségük, vagy anyaguk miatt nehezen, vagy egyáltalán nem mérhetők izotópos berendezéssel, emiatt igen nehezen, vagy egyáltalán nem minősíthetők a hagyományos tömörségmérési módszerekkel.
E tanulmány kimutatta, hogy dinamikus modulus meghatározásánál a sűrűség, víztartalom és tömörségi fok pontos ismerete nélkül nem lehet mértékadó minősítő eredményt szolgáltatni. Ha a dinamikus teherbírást pontosan kívánjuk meghatározni, netán összefüggését vizsgálni a statikus teherbírás E2 értékével, akkor ezek nélkül a korrekciók nélkül a következtetések, összefüggések nem tekinthetők megbízhatónak. Ezek a korrekciók annál durvábbak, minél nagyobb a választott bázistól való eltérés. A dinamikus modulusok számításakor a korrekciót minden esetben figyelembe kellene venni. Csak emiatt a mért értékek akár 10-20%-kal is eltérhetnek a mértékadó minősítő értéktől, nem beszélve arról, hogy egységes követelményünk van a teherbírási határértékre, nem pedig anyagonkénti.
Megállapításaink értelemszerűen adaptálhatók valamennyi dinamikus mérőeszközre, mint a nagytárcsás LFWD és az FWD (KUAB, Dynatest) mérőeszközökre. Ezek korrekciójával jelentős előrelépés tehető az összefüggések újravizsgálásával.
Azok a törekvések, melyek a minősítéseket a dinamikus teherbírás mérésével, a tömörség meghatározása nélkül kívánják megoldani, ezzel az elmélettel nem támaszthatók alá: szükség van a tömörségi fok ismeretére ahhoz, hogy a mért dinamikus modulust a mértékadó minősítő modulusra átszámítani lehessen.
A tanulmány igazolta, hogy valóban elegendő egy dinamikus teherbírási határérték megszabása az előírásokban, tenderekben, nem kellene anyagtípusonként külön szabályozni ezeket, ha a mért értékeket mértékadó minősítő értékre korrigáljuk.
Kijelenthető, hogy a dinamikus teherbírás pontos értéke nem határozható meg a tömörségi fok, a víztartalom és a sűrűség pontos ismerete nélkül.
B&C berendezés alkalmazásánál igen egyszerű a tömörségi és a víztartalmi eltérések miatti korrekció, mert valamennyi ehhez szükséges adat inputként szerepel, számítható. Ismert az anyag, a Proctor legnagyobb száraz sűrűség, az optimális és mért víztartalom, valamint a tömörségi fok. Egyértelműen előnyös és javasolt a jelenlegi vizsgálatok alapján a B&C berendezés szélesebb körű alkalmazása és használata, különösen frekventált, magas minőségi követelményű helyeken.
A mért dinamikus modulus korrekcióját a D=300mm tárcsaméretű, úgynevezett nagytárcsás BP-LFWD berendezéseknél is alkalmazni szükséges. Korrekció nélkül ugyanis nem alkalmasak az egyedi eredmények megfelelő pontosságú mértékadó, minősítő eredmény előállítására. Több mérésből képzett mértékadó eredmény szabványosítása (mint a B&C esetén) sem oldja meg a korrekció problémáját, attól nem lehet eltekinteni, ezért a sűrűség-korrekciót az új mérési szabvány alkalmazza [1].
Bebizonyosodott, hogy a B&C SP-LFWD berendezés használata előnyös akkor is, ha tömörséget nem kell meghatározni, csak teherbírást. A tanulmány felveti annak szükségességét, hogy minden esetben mérjünk a dinamikus modulus mellé tömörséget. Ez a B&C berendezéssel gyakorlatilag 6 helyett 10 ejtést jelent, azaz minden feltétel nélkül könnyen megoldható.
A tanulmány kimutatta, hogy helyszíni relatív dinamikus tömörségi fok TrE% tekintetében általában (pernye kivételével) nem kell korrekció, mert a sűrűségi eltérések hatása a dinamikus tömörség-mérési eredményekre minimális. A hatás jelentéktelen amiatt, hogy a számítás csak a süllyedési amplitúdók különbségét, a maradó alakváltozást veszi figyelembe.
Az építőmérnöki geotechnika nem nélkülözheti sem a teherbírás, sem a tömörség ismeretét, egymásra való hatásuk ellenére. A teherbírásra vonatkozó határérték teljesülése ellenére történhet utántömörödés, süllyedés, illetve jelen tanulmánnyal igazoltan valóban megtörténhet, hogy a mérési eredmény látszólagosan kielégíti a teherbírási határértéket, valójában azonban nem megfelelő. Ehhez a szükséges korrekció elvégezhető jelen tanulmány alapján és a mértékadó minősítő eredmény megbízhatóan számítható. Ennek kell elérni az előírt teherbírási határértéket.
A minőség-ellenőrzés, minőségtanúsítás ma már nem nélkülözheti a kellően pontos méréseket. A megfelelőség ellenére hibásnak minősített munka (felesleges javítási költsége miatt) éppúgy kerülendő, mint a jónak minősített, de valójában nem megfelelő minőség. Az előírást nem kielégítő földmunka meghibásodáshoz vezet, mely mindig és jól láthatóan megbosszulja magát. A nem megfelelő alapok utólagos javítása igen nehéz, nyugodtan mondhatjuk, egy rémálom. Autópályáinkon sajnos gyakran látjuk viszont a deformációt, süllyedést, a minősítő mérések „megfelelősége” ellenére.
A B&C berendezés és elméletének folyamatos fejlesztése lehetővé teszi a korrekt minőségtanúsítást, megelőzve a viszonyítási sűrűségen alapuló tömörségi fok körüli vitákat és tisztázza a valóban lehetséges eltérések okát. Mivel a jelenlegi műszaki elemzés is kimondottan előnyös tulajdonságokat mutat a B&C berendezés javára, ezért annak széleskörű alkalmazását ajánljuk.
Irodalomjegyzék
[1] CWA 15 846:2008 Measuring Method for Dynamic Compactness & Bearing Capacity with SP-LFWD
[2] MSZ 15843:2015 Dinamikus tömörség-és teherbírás mérés SP-LFWD berendezéssel (Measuring Method for Dynamic Compactness & Bearing Capacity with SP-LFWD)
[3] MSZ 15320 Földművek tömörségének meghatározása radioizotópos 46 módszerrel (Determination of the compactness of earthworks by radioisotopic method)
[4] MSZ EN 13286-2 Kötőanyag nélküli és hidraulikus kötőanyagú keverékek 2. Vizsgálati módszerek a laboratóriumi viszonyítási térfogatsűrűség és víztartalom meghatározására. Proctor-tömörítés. (Mixtures without binding material and with hydraulic binding material 2. Test methods for the determination of the laboratory reference volume density and water content. Proctor-compaction)
[5] e-UT09.02.35, ÚT 2-2.124 Dinamikus tömörség és teherbírás mérés kistárcsás könnyűejtősúlyos berendezéssel (Dynamic compactness and bearing capacity measurement with small-plate light falling deflectometer)
[6] e-UT09.02.32, ÚT 2-2.119 Teherbírásmérés könnyűejtősúlyos berendezéssel /Measuring of Bearing Capacity with Light Falling Weight Deflectometer.
[7] TP BF-StB Part 8.3 Dynamic Plate-load Testing with Aid of the Light Drop-weiht Tester./ Dinamikus tárcsás teherbírás mérés, könnyű ejtősúlyos mérőberendezés alkalmazásával
[8] ASTM E2835-11 Standard Test Method for Measuring Deflections using a Portable Impulse Plate Load Test Device./ Standard mérési eljárás behajlás mérésére hordozható dinamikus tárcsás mérőberendezéssel
[9] Brandl, H. and Adam, D. (2004) Basics and Application of the Dynamic Load Plate Test in Form of the Light Falling Weight Device. A.W. Skempton Memorial Conference. Proc. of Imperial College, London.
[10] Dr Boromisza Tibor: Talajmechanika, Alapozás I Szakközépiskolai Tankönyv
[11] Dr Boromisza Tibor, Bertz Gyula Ébényi Miklós: Építőanyagok. TK 1974 Az építőipari, az út- és vasútépítési, a vízügyi szakközépiskolák számára
[12] Subert (2015): CWA15846:2008 Modification Draft and Main Background Studies. Engineering Geology – Rock Mechanics 2015 Congress. BMGE Hungary. p.:379-394
[13] Subert (2015): Önellenőrzés – Stabilizációk tömörség és teherbírás mérése / Self control – Compaction-rate & Bearing Capacity Measuring on Stabilizations. Kézdi Á Konferencia Budapest 2015
[14] Subert (2015): Egyszerűsített és módosított Proctor-vizsgálati eredmények összehasonlítása. Hozzászólás Dr Szendefy János – Vámos Máté cikkéhez. Műszaki Ellenőr-Építési Hibák kiadványa Mélyépítés és Geodézia 2015/05
[15] Subert I: ER-TRG01 Ellenőrzési rendszer próbatömörítések végrehajtására és értékelésére az M7 Zamárdi–Balatonszárszó szakszán. (Control system for the implementation and the evaluation of test compactions on the road section of M7 between Zamárdi and Balatonszárszó/ Mérnöki Eljárási Utasítás. p.10)
[16] Subert at al: Az izotópos és dinamikus tömörségi fok szórás-analízise (Analysis of Standard deviation of the isotopic and the dynamic compactness rate)
[17] Subert at al: Proctor-vizsgálatok új értelmezési lehetőségei. (Options for new interpretations of Proctor-tests) Mélyépítéstudományi Szemle, 2007.
[18] Subert: Method for measuring Compactness-rate with New Dynamic LFWD. XIII. Danube-European Conference on Geotechnical Engineering Ljubljana, Slovenia, 2006
[19] Subert I.: „Dinamikus tömörségmérés a hazai autópályákon és városi helyreállításokon” (Dynamic compactness measurement on Hungarian highways and urban reconstructions) Geotechnika Konferencia 2006 Ráckeve. (2006. október 17-18.)
[20] Fáy M., Király Á., Subert I.: Közúti forgalom igénybevételének modellezése új, dinamikus tömörség- és teherbírásméréssel. (Modelling of the straining of public road traffic by the new, dynamic compactness and bearing capacity measurement) Városi Közlekedés 2006
[21] Fáy M., Király Á., Subert I.: Egy földmű-tömörségi anomália feltárása és megoldása. (Presentation and solution of an anomaly of earthwork density’) Mélyépítéstudományi Szemle 2006
[22] Subert I.: „Dinamikus tömörségmérés aktuális kérdései. A dinamikus tömörség mérés újabb tapasztalatai” (Recent issues of dynamic compactness measurement. New experiences of the dynamic compactness measurement) Geotechnika Konferencia 2005 Ráckeve. (2005. október 18–20.)
[23] Subert I.: „Új, környezetkímélő, gazdaságos mérőeszközök a közlekedésépítésben” /’New, environmental-friendly, economical measuring instruments in traffic building’/ Geotechnika Konferencia 2004 Ráckeve. (2004. október 26–27.)
[24] Subert I.: „A dinamikus tömörség- és teherbírásmérés újabb paraméterei és a modulusok átszámíthatósági kérdései” (Recent parameters of dynamic compactness and bearing capacity measurement and recalculation issues of moduluses) Közúti és Mélyépítési Szemle, 55. évf. 2005. 1. sz. (5 oldal)
[25] Subert I.: „B&C dinamikus tömörségmérés” (B&C dynamic compactness measurement) Mélyépítés 2004 október–december (p. 38–39)
[26] Z.Tompai: Laboratory ecaluation of B&C small-plate light falling weight deflectometer. Periodica polytechnica, Civil Engineering 52/2 (2008) 103-107. p.:103-107
e-UT 06.02.11 (ÚT 2-1.222) Utak és Autópályák létesítésének általános geotechnikai szabályai.
e-UT 06.03.52 (ÚT 2-3.207) Útpályaszerkezetek kötőanyag nélküli és hidraulikus kötő- anyagú alaprétegei.
e-UT 06.03.23 (ÚT 2-3.307) Kohósalakaszfalt útpályaalapok és burkolatok 11.
e-UT 05.02.41 (ÚT2- 3.603) Pernye alkalmazása útépítési kötőanyagként
