https://doi.org/10.36246/UL.2024.2.02
2024; 12. évfolyam, 20. szám
Bevezető gondolatok
A közútkezelők tevékenységéhez feltétlenül szükséges, hogy információik legyenek a kezelt utak különböző tulajdonságairól. Ezek meghatározására innovatív módszereket és eszközöket használnak. A talán legfontosabb dolog, amit a tulajdonságok rendszeres megfigyelésével meg lehet állapítani, az az időtartam, amíg ezek a tulajdonságok valamilyen előírásnak megfelelnek.
A szerző pályája során számos ilyen információ forrásával és lehetőségével találkozott. Ezek közül az ejtősúlyos behajlásmérő (Falling weight deflectométer, FWD) képességeit és lehetőségeit találta a leginkább hasznosnak.
Tapasztalatait ezért egy cikksorozatban kívánja megosztani a lehetséges felhasználókkal.
A cikksorozat a következő részekből áll:
- Első rész: A készülék és képességei
- Második rész: Az elválaszthatatlan földmű és pályaszerkezet
- Harmadik rész: Pályaszerkezeti rétegek
Bevezetés
Az útépítés szerkezeteinek egyik fontos tulajdonsága a merevség, amit közvetetlenül nem lehet meghatározni, ezért a kérdéssel foglalkozó mérnökök különböző, közvetett módszereket fejlesztettek ki.
A helyszíni vizsgálatok közül a tárcsás mérés [1] tekinthető elsőnek, majd Alvin Carlton Benkelmann kifejlesztette a billenőkaros behajlásmérést [2], ami valóságos forradalmat hozott a pályaszerkezet gazdálkodásban.
A tapasztalatok és az egyre nagyobb merevségű pályaszerkezetek tulajdonságai két problémát vetettek fel:
- egyrészt világossá vált, hogy a teljes behajlási teknő alakja fontos információkat hordoz az egyes pályaszerkezeti rétegek tulajdonságairól, tehát célszerű volna ennek meghatározása is
- másrészt világossá váltak az ellensúlyos eljárások korlátai a „hatásmélység”, azaz a mérésből következő információs határok szempontjából [1].
Egyéb tényezők mellett ezek vezettek a szeizmikus módszerek használatának irányába és az FWD készülék kifejlesztésére [3], utóbbi rövid FWD „történelmet” is tartalmaz.
A berendezésről néhány szó
A mérési elv és a mérés
Az FWD mérést szakmai szóhasználatunk „dinamikus” mérésnek nevezi, amely megnevezés helytelen. A mérés szeizmikus elven áll, ahol a gerjesztő impulzus hatására a vizsgált térrészben hullámok keletkeznek, a következő ábra szerint.
 |
Az FWD készülék működésének jellegrajzát vizsgálhatjuk a következő képen. Az impulzust adó tömeg (rugós csillapítással) ráesik a terhelő tárcsára. A generált hullámfront halad sugárirányban és sorra eléri a behajlásokat mérő szenzorokat, amelyek az értéket rögzítik.
 |
A készülék folyamatosan rögzíti az alakváltozásokat (és a terhelő erőt) az idő függvényében, eredménynek pedig az egyes érzékelőkön elért maximumot adja meg, amely különböző időpontokban keletkezik, ezt láthatjuk a következő ábrán.
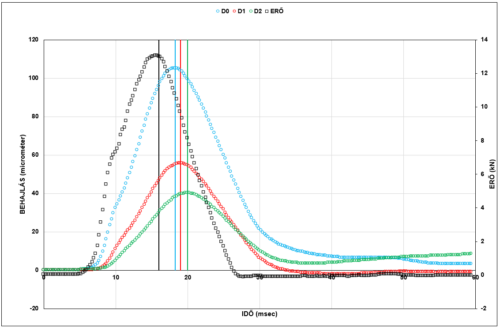 |
A mérés tehát egy szeizmikus eljárás, annak több előnyével:
- A mérés mentes a talphibától, azaz attól, hogy a viszonyítási sík beleesik a terhelési teknőbe, ezáltal a mért behajlás hibával terhelt
- Pályaszerkezeti anyagaink a szokásos terhelési idők miatt meglehetős pontossággal rugalmasan válaszolnak.
- A [4] szerint a semleges feszültségeknek (pl. telítettségközeli állapot) nincs hatásuk a hullámterjedésre és ezáltal az eredményekre.
A mérés eredményei
Behajlások
A legfontosabb eredmények az egyes érzékelőkhöz tartozó behajlások, ezek összessége egy mérési ponton adja meg a behajlási teknőt.
 |
A gyakorlatban nagyon sokszor használjuk a fontosabb érzékelőkhöz tartozó behajlások különbségét, ezeket hívjuk teknőparamétereknek ezeket is tanulmányozhatjuk a 4. ábrán.
Ezek használatával pl. az aszfaltszerkezetben keletkező megnyúlások is számíthatók [5].
Hiszterézisgörbék
Kevéssé ismert, hogy a készülék rögzíti a behajlás/terhelés (erő) értékeket a teljes terhelési ciklusban. Ez tulajdonképpen a mérési ponton értelmezhető hiszterézisgörbe, amelynek területe fontos, sok mindenre jellemző érték, ezt is láthatjuk az 5. ábrán.
A három különböző pályaszerkezeten történt méréssel fizikailag értelmezhető módon lehet megkülönböztetni pl. a makadám, hajlékony, félmerev csoportba tartozó pályaszerkezeteket is.
A hiszterézisgörbék tanulmányozásával fontos információkhoz lehet jutni [6], a görbe alatti terület munka dimenziójú és a hivatkozás szerint arányos a fáradással, erre a kérdésre a pályaszerkezeti rétegekre vonatkozó cikkben visszatérünk.
 |
Terhelés, terhelési idő, terhelő felület
A felhasználás céljai gyakran megkívánják, hogy bizonyos képességek változtathatók legyenek, néhány ilyenről lesz szó a következőkben.
Terhelés
A valós járműterhelések rongáló hatását lehet bizonyos etalon terheléssel helyettesíteni. A mechanikai pályaszerkezet – modellezés gyakran megkívánja a valóság pontosabb leírását.
Az egyik legkézenfekvőbb változtatási szükséglet a terhelés differenciálása.
A 6.ábrán ugyanazon pályaszerkezeten különböző terhelő erők alatti behajlásértékeket lehet vizsgálni (három terhelés esetén a „fél” behajlási teknő van ábrázolva.
Az ábra esetére számítottuk az aszfaltréteg alsó szálában keletkező megnyúlásokat is.
Különösebb részletezés nélkül is belátható, hogy a különböző „hatványos átszámítású” egyenértékű terhelőkerék (hazánkban 50 kN) által okozott „rongáló hatás” (megnyúlás) közel sem a megszokott, tankönyvekben szereplő különbségeket mutatja. Az összefüggések bizony pályaszerkezetenként különböznek és a valós tönkremenetelek prognosztizálásánál célszerű a realitás határain belül a teljes terhelési spektrumot figyelembe venni, erre később még visszatérünk.
A kereskedelmi forgalomban lévő eszközök döntő része képes a terhelés változtatására.
 |
Terhelési idő
Pályaszerkezeti anyagaink merevsége a terhelési időtől függ. Ez főleg aszfaltszerkezetein esetében lényeges.
Eszközeink egy része képes a terhelési idő változtatására, bizonyos határok között.
A KUAB berendezésre van Gurp [5] kidolgozott egy eljárást a standard terhelési időből való átszámításra.
 |
A 7. ábrán három különböző mérési pont esetében kiszámítottuk az eredeti 60 msec terhelési időhöz tartozó behajlásértékből a 25 msec terhelési időhöz tartozó behajlást.
A látszólag csekély különbség fontosságát jobban érzékelteti a következő ábra.
 |
Az értékeket egy vissza – számoló eljárás segítségével aszfaltmerevségre konvertáltuk, ezt a 8. ábrán ábrázoltuk. Jól látható, hogy a csekély behajláskülönbség egyes esetekben meglepően nagy merevségkülönbséget „okoz”.
A módszerrel az alacsonyabb sebességű forgalmi terhelés hatása jól modellezhető, nyilván ebben az esetben a merevség csökkenésével megnőnek az aszfaltrétegben a megnyúlások, ezáltal az élettartam csökken.
Terhelő felület
A terhelő felületnek a mérete, illetve a teherátadás szempontjából fontos a merevsége, ez határozza meg (részben) a terhelő felület alatti feszültségeloszlást.
A terhelő felület változtathatósága – saját tapasztalat alapján – viszonylag ritkán merül fel, a „nagy” berendezéseknél.
A kisebb, kézi kezelésű berendezéseknél ez több típusnál is megoldott.
A behajlási teknő alakja
A behajlási teknő alakjának matematikai megfogalmazására több kísérlet is történt, a gyakorlatban nagyon jól használható eljárást ismertet [7].
A módszer a behajlási adatokból számítható alaktényezőre és a központi behajlásra, mint paraméterre alapul.
Vizsgáljuk meg a két paraméter hatását a következő ábra alapján.
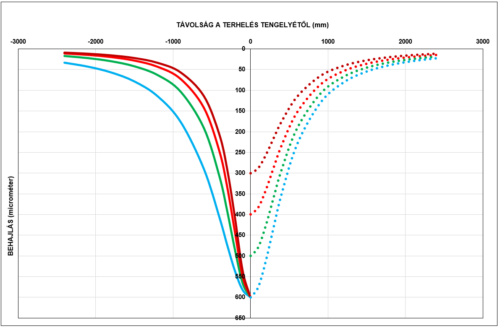 |
Látható, hogy az egyik paraméter rögzítésével milyen a behajlási teknő alakjának változása.
A módszer komoly gyakorlati lehetőségeket ad, így pl.
- lehetséges a behajlás meghatározása érzékelővel nem rendelkező helyen, ennek a jelentőségét a következő, a földmű/pályaszerkezetes cikkben láthatjuk, ahol mind az extrapolálás, mind az interpolálás szerepel az esettanulmányokban
- kézi eszköz használatára ad lehetőséget, amelynek viszonylag kis szenzortávolságú helyeiből számítható a teljes behajlási teknő (az utánfutós eszközzel nem járható helyeken, vagy pl. keresztirányban ad mérési lehetőséget egy kézi eszköz)
- végül ad egy kiegyenlítő (a kiugró értékeket kiszűrő) lehetőséget az, hogy a mért értékek helyett a számított értékekkel dolgozunk, szerző ezt rutinszerűen alkalmazza a behajlásmérők egyes pontjain jelentkező mérési bizonytalanság kiküszöbölésére
A mérés helye
A mérés helyével kapcsolatos kérdéseket a földmű/pályaszerkezet kombinációval foglalkozó cikkben részletezzük.
Meteorológiai és statisztikai kérdések
Az eszköz használatával keletkező jelentős mennyiségű adat feldolgozásánál új szempontokat kell figyelembe venni és új eljárásokat kell használni.
Meteorológiai tulajdonságok
A felhasználó szempontjából két dolgot kell kiemelni, a mérés ismételhetőségét és a különböző eszközök által szolgáltatott eredmények összehasonlíthatóságát.
Megjegyzendő, hogy ezeket a tulajdonságokat csak azonos mérési pontok esetében lehet korrektül értelmezni, így a különböző eszközök képességeinek összehasonlításánál más eszközöket kell alkalmazni.
Az ismételhetőséggel kapcsolatban [3] alapján megállapítható, hogy az nagymértékben kielégítő.
Az összehasonlíthatóság, a hivatkozott tanulmány szerint leginkább a gumiütközők tulajdonságaitól függ, ez viszont az eszköz típusának függvénye.
Kicsit leegyszerűsítve kijelenthető, hogy egy szakasz esetében nem célszerű különböző típusú eszközök használata, ez általánosítva értelmezhető egy államra is.
Homogén szakaszok
A mérést jellemzően hosszabb szakaszokon végezzük és minden esetben ezen teljes szakaszon belül a tulajdonságok homogenitása fontos kérdés, ennek jó meghatározására alkalmas a következőkben ismertetett módszer.
Olyan adathalmazok esetében, ahol az egyes mintaelemek egymáshoz képest térben vagy időben rendezettnek tekinthetők (tehát nem cserélhetők fel) az adathalmaz homogenitását jól jellemzi az ún. kumulatív összeg.
A kumulatív összeg értékek az egyes mintaelemeknél a következőképpen számíthatók ki:
S1 = x1 – xátlag
S2 = x2 – xátlag + S1
Si = xi – xátlag + Si-1
Miután a különböző ismérvek Si értékei akár nagyságrendekkel is eltérhetnek egymástól, célszerű azok normált értékeit használni (ez azt jelenti, hogy a Si értékeket 0 és 1 között értékekre alakítjuk át)
A normálást a következőképpen lehet végrehajtani.
Snormált, i = (Si – Smin)/Smax – Smin)
ahol Smin, Smax az Si értékek minimum és maximum értéke.
A kumulatív összeget pontonként kiszámítva és diagramban ábrázolva a teljes szakaszon a homogén rész – szakaszok megkülönböztethetők, úgy, hogy ott van rész – szakasz határ, ahol a görbe iránytangense előjelet vált.
A használatot egy konkrét példán a következő diagram segítségével mutatunk be.
Létezik olyan FWD készülék, amelyen keresztirányban is vannak szenzorok elhelyezve, egy ilyen berendezéssel, a tengelytől 300 – 300 mm távolságban lévő pontok és a tengelypont adataiból számoltuk az alaktényezőket, ezek kumulatív összeg diagramjait tartalmazza az ábra.
A fekete vonal mutat egy „homogén rész – szakaszt” az ezen az alaktényező segítségével számolt (keresztirányú) földműmerevségeket is feltüntettük.
A kumulatív diagram mutatja, hogy a két alaktényező a homogén részen eltér, az eltérés valószínű oka pedig a burkolatszél felé csökkenő földműmerevség (ez utóbbival a következő cikkben részletesen foglalkozunk).
 |
Tehát a kumulatív összeg módszer képes az egymáshoz képest viszonylag közeli pontok sajátosságainak különbségét (is) megmutatni és egy diagnosztika jellegű probléma esetén viszonylag egyszerűen megtalálni az eltérés okát.
Adatsorok összehasonlítása
Gyakori probléma két különböző módon nyert adatsor eredményeinek összevetése abból a szempontból, hogy milyen közel esnek az azonossághoz.
Ilyen például egy út jobb, illetve bal oldalán mért behajláshalmazok összevonhatósága, különösen érdekes lehet akkor például, ha az egyik adatsor nem FWD mérésből származik és számos hasonló helyzet adódik.
Az összevetést célszerű a percentilisek összehasonlításával kezdeni (ez az Excell egyik segédfüggvénye) a két halmaz azonos percentiliseinek összehasonlítása lényegében az eloszlásfüggvények hasonlóságát mutatja meg.
A következő ábrán megvizsgálhatjuk a két adatsor kapcsolatát, a trendvonal alakja és a matematikai kapcsolat szorossága lényegében azonosságot mutat.
 |
Átszámíthatóság
Az FWD technológiával kapcsolatos szakirodalom rengeteg átszámítással foglalkozó képletet tartalmaz, elsősorban a Benkelmann tartóval végzett behajlásmérésekre. A szerző nyomatékosan állítja, hogy a kidolgozott megoldások szorosan csak a konkrét esetre vonatkozhatnak és számos tisztázatlan kérdés marad homályban, ezért nem tartja célszerűnek (és szükségesnek sem) az átszámításokat.
Berendezési típusok
Számos berendezéstípus létezik, világviszonylatban is kevés szakosodott gyártó állít elő kisebb sorozatokban eszközöket.
Számos, kifejezetten egyedi célú berendezés mellett három csoport különböztethető meg:
- kézi alkalmazású berendezés, ezek a nehezen megközelíthető helyeken nagyon hasznosak, eredményeik az azonos elv miatt teljesen kompatibilisak az utánfutós berendezésekével
- utánfutón működő berendezés, itt létezik specializálódás a hagyományos pályaszerkezetre optimalizált és a repülőtér/konténerrakodó vastagabb beton szerkezetekre kifejlesztett berendezések között
- „nagy sebességű” berendezések, itt már a hordozó jármű saját tömegereje által kiváltott deformációkat rögzítik. Ez a módszer nem a szeizmikus kategóriába tartozik, a nagy teljesítmény és a biztonság igénye hozta létre. Eredményeinek feldolgozása speciális matematikát igényel, itt csak a teljesség miatt van megemlítve.
A „szabványos” utánfutós berendezések legújabb fejlesztési irányai között megemlítendő a lokális fárasztásra alkalmas berendezés, kellően nagy erővel meglepően nagy egységtengelyszám érhető el rövid idő alatt.
 |
Az eredmények felhasználása
Az írás végén néhány esettanulmányt közlünk, a sorozat további részeiben elég részletesen lesz taglalva a készülék és a technológia lehetőségeinek halmaza.
Szintetikus pályaszerkezetek
Az FWD technológia korábbi periódusában a behajlási adatokból nagyon népszerű volt a vissza – számolás, azaz az egyes rétegek merevségének iterációs szoftverekkel történő megállapítása.
Ezekből az adatokból aztán méretező programok segítségével számítottak megnyúlást/feszültséget, viszont az eljárásnak voltak matematikai problémái [8].
Részben emiatt is de hamarosan felmerült [5] a behajlási adatokból (teknőparaméterekből) történő megnyúlás/feszültség meghatározás lehetősége.
Az innovatív mérnökök ezek után megalkották a szintetikus pályaszerkezetet, ahol előre megadott kombinációkban számos (százas nagyságrendben) pályaszerkezetet számoltak ki valamilyen méretező szoftverrel, pl. az FWD által meghatározott szenzortávolságokban a behajlások értékeivel.
Ilyen munka volt a [9] alatti gyűjtemény létrehozása, aminek adataiból aztán számos hasznos összefüggést lehetett létrehozni, ilyen összefüggés például a már említett alaktényező meghatározásának lehetősége az SCI, illetve BCI teknőparaméterek hányadosának segítségével.
Az alaktényező fontosságáról már volt szó, meghatározása a következő ábrán lévő összefüggéssel lényegesen egyszerűbb.
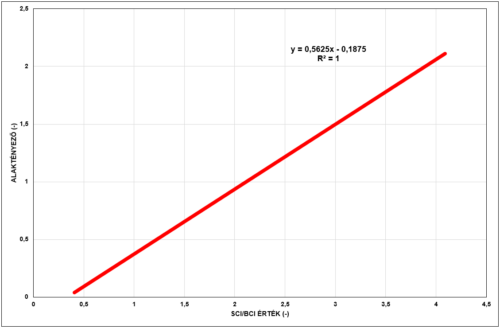 |
Mostanság a szintetikus pályaszerkezetek generálása már teljesen rutinszerű, a [10] alatti kutatás eredményeként a hajlékony pályaszerkezetek rétegeinek lényegében minden érdemi igénybevételét illetve anyagtulajdonságát ki lehet számolni a behajlási teknő paramétereiből.
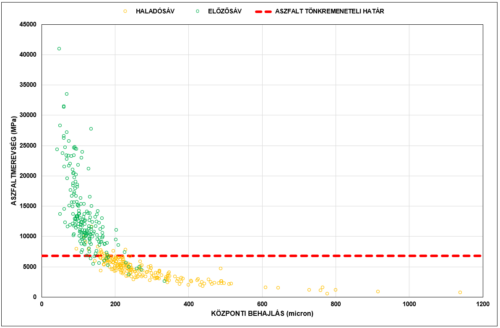 |
A technológia napjainkban is tovább fejlődik, egyre több kutatás foglalkozik a mesterséges adatbázisokban való „adatbányászattal”, amivel fontos problémákat lehet megoldani.
Esettanulmány 1
A szerző tapasztalatai azt mutatják, hogy az építőmérnöki mentalitás alapvetően tapasztalati, ezért bonyolult elméleti fejtegetések helyett esettanulmányokon keresztül kívánja az FWD készülék lehetőségeit stb. bemutatni.
Egy jelentősebb útépítésen az alapréteg felületén 300 MPa E2 érték volt előírva, amely az aszfaltozás előtt ellenőrizték és számos helyen a követelmény nem teljesült.
A bizonytalan helyzet miatt ejtősúlyos berendezéssel is meghatározták a merevséget és az értékeket a d600 – d900 teknőparaméter függvényében ábrázolták, ez látható a 15. ábrán.
 |
Ez a teknőparaméter az alapréteg felső síkja alatti 600 – 900 mm mélységben lévő földmű/javítóréteg merevségére jellemző.
A kiértékelés után az alapréteg elbontását rendelték el és a bontásnál a 16. ábra szerinti helyzet volt látható.
 |
Azaz, az alapréteg alatti javítóréteg (és a földmű is) közel telített állapotban volt (egy szivárgó hibája miatt).
Vegyük észre, hogy az ejtősúlyos berendezés „hatásmélysége” itt legalább 6 – 900 mm között volt és egy súlyos, későbbi hibát lehetett ezzel megakadályozni.
Esettanulmány 2
Egy gyorsforgalmi úton, ideiglenes terelés alatt tapasztalták, hogy a leállósávon súlyos hibák keletkeztek.
 |
Az ejtősúlyos mérés alapján számítottuk a kötött rétegek (CKt + aszfalt) merevségét, ez látható a 18. ábrán piros színnel. Feltűnő, hogy az értékek két rövidebb szakaszon lényegesen magasabbak, a többi részen viszonylag hasonlóak.
Számítottuk a kumulatív összeget és kék színnel lett ábrázolva.
Jól kivehető, hogy négy, homogénnek tekinthető rész – szakaszból áll a teljes vizsgált rész.
Csak az eljárás robusztusságának bemutatására, az első, hosszú ferde CUMSUM vonalba tartozó merevségértékek relatív szórása 0,36, ami lényegesen kisebb, mint a gyakorlatunkban a homogenitás feltételének tekintett 0,5.
A kiugró értékek helyei (kétféle sárga színnel jelölve) azonosak a közbenső csomópont miatti lassító és gyorsítósávval.
Ilyen összeesések nem tekinthetők véletlen eseménynek, a forgalmi sávként működő helyeken magasabb volt a cementadagolás, mint a leállósávos helyeken, ennek okai nyilvánvalóak.
Vegyük észre, hogy a következtetéshez a nagyon hatásos statisztikai módszer segített hozzá.
 |
Esettanulmány 3
Különösen nagyforgalmú utak esetén a felújításnak – ráépítésnek – számos hátránya van, így a legelső az, hogy a forgalommal nem, vagy alig terhelt helyeken az azonos szint biztosítása gazdaságtalan.
A [11] alatt egy ilyen helyzet méretezési kérdéseit elemezte a szerző, itt csak egy ábrán bemutatjuk a tényleges helyzetet.
A probléma a nem megfelelő réteg eltávolítása után a visszaépítés méretezési megfelelőségének vizsgálata.
Nos, az FWD technológiával a probléma megoldható. Az ábrán az eredeti, a marás utáni és a visszaépítés utáni egyenértékű felületi modulusokat vizsgálhatjuk, jól látszik, hogy az új felületen a merevség lényegesen nagyobb és ezeket az eredményeket az első mérés adataiból lehetet prognosztizálni, a prognózist a további mérési eredmények megerősítették.
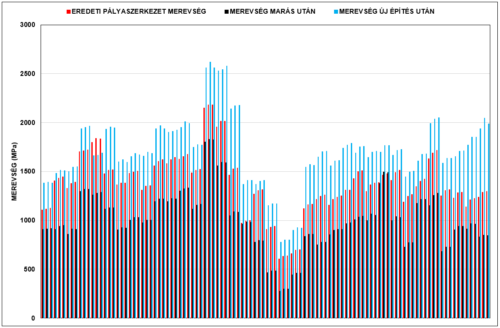 |
Hivatkozások
[1]: MSZ 2509/3 1989 Tárcsás mérés
[2]: MSZ 2509/4 1989 A behajlás mérése
[3]: European Cooperation in the Field of Scientific and Technical Research COST 336 Use of Falling Weight Deflectometers in Pavement Evaluation Final Report of the Action Main Report 2nd Edition – April 2005
[4]: Törös, E. 2006. A szeizmikus módszer geotechnikai alkalmazásainak kritikai vizsgálata. PhD értekezés
[5]: Van Gurp. C.A.P.M. & Wennink, P.M. 1997. Design, structural evaluation an overlay design of rural roads (in Dutch) KOAC – WMD consultans; Apeldoorn
[6]: D. Ayyala, H. Lee, & H. L. Von Quintus. 2018. Characterizing Existing Asphalt Concrete Layer Damage for Mechanistic Pavement Rehabilitation Design FHWA-HRT-17-059
[7]: Primusz, P. & Tóth, Cs. 2009. A behajlási teknő geometriája. In: Közlekedésépítési Szemle 59.12, pp. 18-24, 28
[8]: Grätz, B. 1999. Az ejtôsúlyos deflektométerek lehetôségei és határai az útpályaszerkezetek értékelésénél, Közúti és Mélyépítési Szemle, XLIX. évfolyam, 6. szám, pp. 236–239
[9]: Primusz, P. & Markó, G. 2010. Kétrétegű pályaszerkezet-modellek paramétereinek meghatározása FWD-mérések alapján Közlekedésépítési Szemle.
[10]: Y. R. Kim & H. Park. 2002. Use of FWD Multi-Load Data for Pavement Strength Estimation. Performing Organization Name and Address Campus Box 7908, Department of Civil Engineering 10. Work Unit No. (TRAIS) North Carolina State University
[11]: Karoliny, M. 2018. Útpályaszerkezeti esettanulmányok: A szilárdságtani módszerek és a valóság Útügyi Lapok.
Erre a szövegre így hivatkozhat:
Karoliny Márton: Pályaszerkezetek tulajdonságainak meghatározása FWD készülék segítségével. Első rész: A készülék és képességei, DOI: 10.36246/UL.2024.2.02
