Pdf: Hidak állékonyságának biztosítása szeizmikus terhekre – esettanulmányok
Bevezetés
Az Eurocode szabványsorozat bevezetésével Magyarországon is előtérbe került hídszerkezeteink földrengési hatásokra történő tervezése. Általános földrengés méretezési elvekkel az Eurocode 8 1. része (EC8-1) (MSZT, 2008), míg a hidak szeizmikus méretezésével az Eurocode 8 2. része foglalkozik (EC8-2) (MSZT, 2006). A korábban készült szeizmológiai adatok szerint Magyarország alacsony szeizmicitású régió volt és ennek következtében a korábbi magyar szabványok (Magyar Útügyi Társaság, 2004) nem foglalkoztak a hidak szeizmikus méretezésével, az újabb kutatások szerint (Tóth és mtsai, 2006) Magyarországon, az Eurocode alapú tervezés során figyelembe veendő talajgyorsulás tervezési értéke jelenleg a moderált szeizmicitású kategóriába eső 0,08~0,15 g. A megnövekedett szeizmicitás a tervezői és kutatói tapasztalatok szerint (Zsarnóczay és mtsai, 2013) számos hídkonfiguráció esetén mértékadó hatást jelent.
A fenti körülmények megkövetelik hídszerkezeteink szeizmikus viselkedésének részletesebb elemzését. Zsarnóczay (2010) munkájában a tipikus közúti gerendahíd kialakítások szeizmikus érzékenységét vizsgálta és a kritikus szerkezeti részleteket határozta meg. Simon (2012 a, b) doktori kutatásában meglévő hídszerkezeteink viselkedését elemzi egyszerűsített és fejlett, nem-lineáris analízis alapú vizsgálati módszerekkel. Ezen munkák globális képet festenek hazai hídállományunk szeizmikus érzékenységéről, esetlegesen bekövetkező földrengés okozta károsodások mértékéről, valamint támpontot adnak új hídjaink szeizmikus méretezési koncepciójának későbbi kialakításában és meglévő hídjaink esetleges megerősítési szükségleteinek megállapításában.
Az elmúlt évtizedben több megépült híd méretezése, valamint esettanulmányok további tapasztalatokat szolgáltattak (Vigh és mtsai, 2006; Vigh, 2012; Martinovich, 2011; Dani, 2008).
Első tapasztalatainkat két Duna-híd, a dunaújvárosi Pentele híd és a budapesti Megyeri híd kapcsán szereztük (Vigh és mtsai, 2006). Ezen hidaknál az acélszerkezetű felszerkezet, illetve merevítőtartó esetében a szeizmikus hatások általában nem mértékadóak, míg az alépítmény és alapozás esetében a teherbírási határállapotnál jellemzően 20-30%-kal nagyobb igénybevételek adódtak. A saruk méretezésében a földrengési igénybevételek döntőek. Zsarnóczay (2010) munkája a hasonló méretű és kialakítású gerendahidakra kiterjesztve a fenti konklúziókat megerősítette.
Zsarnóczay (2010) paraméteres vizsgálat keretében több ezer közúti gerendahíd szeizmikus viselkedésének értékelését hajtotta végre, modális válaszspektrum analízis segítségével. Tipikus, a hídtervezésben szokványosnak tekinthető kialakítások feltételezésével meghatározta azokat – az 1. táblázatban összefoglalt – tartományokat, amelyekben a földrengési teherkombináció valamely szerkezeti részletre vagy a híd egészére mértékadó lehet. Az 1. ábra szintén erre mutat példát: az ábra különböző felszerkezetű és pillérmagasságú hidak esetére mutatja azt a maximális talajgyorsulási értéket (MAPGA), amelyre a szerkezet teherbírása modális válaszspektrum analízis alapján igazolható. Az eredmények alapján a szerkezet kritikus pontjai a saruk, a pillérek és az alapozás. Nagyobb hidak esetén a földrengési igénybevételek mértéke általában nem igényel jelentős keresztmetszet-növelést, ugyanakkor alacsony pillérek esetén a földrengési hatás a gyakori hatások 2-3-szorosát is elérheti (Zsarnóczay, 2010).
Amennyiben a hagyományos tervezési koncepció alapján megtervezett és kvázi-rugalmas földrengési analízissel vizsgált szerkezet teherbírása a szeizmikus hatásokkal szemben nem kielégítő, a következő alternatívák közül választhatunk:
- a szerkezetet a kapott igénybevételekre megerősítjük,
- fejlett, nem-lineáris analízis segítségével igazoljuk a szerkezet állékonyságát,
- csillapító eszközöket, szeizmikus szigetelést alkalmazva csökkentjük a földrengési terheket
A következőkben mintapéldán keresztül mutatjuk be a fejlett analízis alkalmazásának mikéntjét, hatékonyságát és korlátait, valamint egy új szerkezet tervezése és egy meglévő szerkezet utólagos megerősítése esetében hasonlítjuk össze a hagyományos és innovatív (csillapítóelemes) megerősítési módozatokat.
| Felszerkezettípus | Pillérmagasság (m) | Fesztáv (m) |
|---|---|---|
| monolit vb. | <17 | 8-40 |
| előregyártott vb. | <18 | 8-45 |
| vb. szekrény | <18 | 18-50 |
| öszvér | <17 | 20-90 |
| acél főtartó (+ortotrop pálya) | <18 | 40-120 |
| acél szekrény | <18 | 40-150 |
 |
Analízis módszerek összehasonlítása
Az EC8-2 többtámaszú hidak vizsgálatára jellemzően a következő analízis módszereket ajánlja, illetve követeli meg:
- modális válaszspektrum analízis,
- eltolás vizsgálat (nem-lineáris statikai analízis),
- időtörténeti vizsgálat (nem-lineáris dinamikai – time-history – analízis) tényleges vagy mesterséges földrengés rekordok figyelembevételével.
A modális válaszspektrum analízis során annyi rezgésalakot kell figyelembe vennünk, hogy a rezgésalakokhoz tartozó modális tömegarányok összege a teljes szeizmikus tömegnek legalább 90%-át elérje. Az egyes rezgésalakokhoz külön-külön határozzuk meg a helyettesítő statikus terheket, amelyek statikai analíziséből kapott igénybevételeket, elmozdulásokat összegezzük pl. négyzetes összegzési (SRSS) módszer alapján. Amennyiben több rezgésalak is domináns (azaz relatíve magas modális tömegaránnyal rendelkezik), úgy a modális válaszspektrum analízis túlbecsüli a tényleges földrengés bekövetkeztekor kialakuló igénybevételeket, hiszen az egyes – egymással nem egy időben jelentkező – rezgésalakokhoz tartozó maximális értékeket vesszük számításba. Mivel az időtörténeti dinamikai analízis a földrengés időbeliségét megfelelően leírja, a fejlett analízis egyidejű igénybevételeket szolgáltat. Emiatt várható, hogy már a lineáris dinamikai analízis is kedvezőbb eredményeket (kisebb igénybevételeket) ad, mint a modális válaszspektrum analízis.
További csökkentés származhat a számított igénybevételekben, ha figyelembe vesszük a szerkezeti elemek anyagi nem-linearitását, képlékenyedését. Ennek feltétele, hogy a képlékenyedés (pl. vasbeton pillér befogási keresztmetszetében) ki tudjon alakulni a szerkezetben, illetve hogy azt a numerikus modellben megfelelően modellezzük. A hazai gyakorlatban megépülő szerkezetek egyes komponensei – a célzottan disszipatív tervezés hiánya ellenére is – rendelkezhetnek képlékeny tartalékkal, illetve bizonyos szintű duktilitással. Vasbeton elemek esetén a tiszta hajlítási tönkremeneteli mód gyakorta számba vehető duktilitás mellett tud kialakulni, de kizárandóak a rideg tönkremeneteli komponensek (pl. a betonfedés leválása, lerobbanása jelentős degradációt jelenthet). A nyírási tönkremenetel mindig rideg, ezért kerülendő (megfordítva: ha a nyírási tönkremenetel mértékadó, a pillér képlékenyedése nem vehető figyelembe).
A következőkben a 2. ábrán látható, az új M0-ás hárosi Duna-hídja esetében hasonlítjuk össze az egyes analízis módszereket. A szekrény keresztmetszetű, folytatólagos, háromnyílású, acél gerendatartót változó keresztmetszetű, tömör, vasbeton pillérek támasztják meg. A nyílások támaszköze 108,5 m. A felszerkezet anyagminősége S355, a pillérek betonminősége C35/45, az alkalmazott betonacélok minősége S500B. A felszerkezet hosszirányban az 5. számú pilléren van lekötve mindkét sarun, míg keresztirányban minden támasznál egy-egy sarun. A figyelembe vett földrengési paraméterek: C talajtípus; 1,0 m/s2 talajgyorsulás, 1. típusú válaszspektrum.
A híd vizsgálatára térbeli rúdmodellt építettünk Ansys környezetben. A modell egy tipikus részletét – pillérfelszerkezet környezetét – mutatja a 2. ábra. A megfelelő földrengési analízishez lényeges a pillérfelszerkezet és a talajszerkezet kapcsolat helyes modellezése. Megjegyezzük, hogy utóbbira a számítás rendkívül érzékeny: a szerkezetre adódó szeizmikus terheket rendkívüli mértékben befolyásolhatja a túl merevnek vagy túl lágynak feltételezett alapozás. A modell további részleteiről lásd Simon (2012) és Simon és Vigh (2012).
 |
A modális válaszspektrum analízis során a 90%-os modális tömegarányt 100 lengésalak figyelembe vételével minden irányban elérjük. A számítások alapján a szerkezet kritikus eleme az 5. pillér, mértékadó igénybevételei a pillértőben: My = 229907 kNm hosszirányú és Mz = 275367 kNm keresztirányú hajlítónyomaték. Ugyanezen a pilléren alakulnak ki a legnagyobb sarureakciók is: hosszirányban Bx = 5045 kN, míg keresztirányban By = 7809 kN. A felszerkezet legnagyobb elmozdulásai rendre 27 mm, 36 mm és 247 mm keresztirányban, hosszirányban és függőleges értelemben.
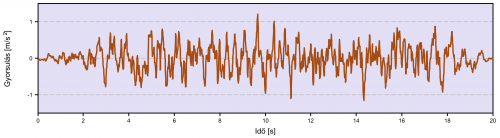
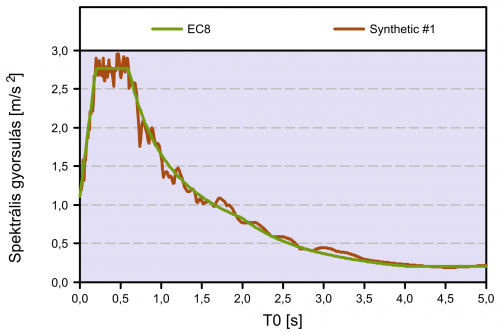
Lineáris dinamikai (time-history) analízis során az EC8-2 szerint mesterséges földrengés rekordok is alkalmazhatóak. A rekordokkal szemben támasztott legfontosabb követelmény, hogy a szerkezet mértékadó rezgésidejeinek tartományában a mesterséges rekord alapján számítható rugalmas gyorsulási válaszspektrum érték illeszkedjen a szabványos rugalmas válaszspektrumra. Mivel esetünkben relatíve sok, tág periódusidő tartományban mozgó lengésalak figyelembevétele volt szükséges, a mesterséges rekordok előállítására olyan eljárás szükséges, mely a válaszspektrum széles tartományában biztosítja az illeszkedést. A Simon és Vigh (2012) által kifejlesztett algoritmussal ez megvalósítható, az előállított talajgyorsulási időfüggvényekre és a rendkívül jó válaszspektrum illeszkedésre mutat példát a 3. ábra.
A lineáris time-history analízis alapján az 5. pillér keresztirányú igénybevételei és a keresztirányú sarureakciók jelentősen – 30-35%-kal –, míg a hosszirányú erők kis mértékben csökkentek: My = 217217 kNm, Mz = 190599 kNm, Bx = 4910 kN, By = 5201 kN. A felszerkezet legnagyobb elmozdulásai rendre 10 mm, 34 mm és 221 mm keresztirányban, hosszirányban és függőleges értelemben.
A keresztirányú hatások jelentős csökkenésének az a magyarázata, hogy keresztirányban sok, egymással nem egyidejű lengésalakot kellett figyelembe venni a 90%-os modális tömegarány eléréséhez, míg hosszirányban néhány lengésalak dominál.
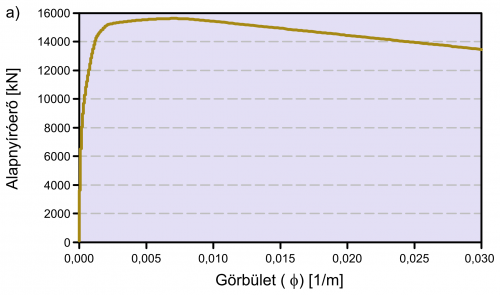
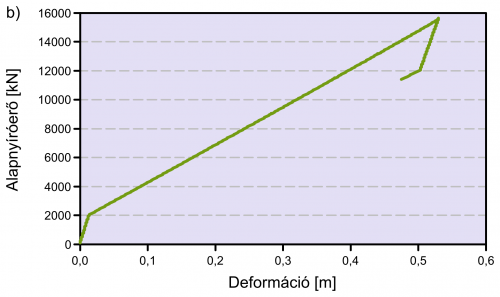
Az anyagi nem-linearitás figyelembe vételével tovább pontosítható a vizsgálat. Képlékenyedés kialakulhat a pillértövekben és a sarukban. (Megjegyezzük, hogy a talaj és alapozás viselkedése is nem-lineáris, ezt a hatást jelen tanulmány nem vizsgálta.) A vasbeton pillér számított és a modellben figyelembe vett nyomaték-elfordulási és a fix és mozgó saruk erő-elmozdulási karakterisztikáit, illetve hiszterézis viselkedését mutatja a 4. ábra. Lényeges, hogy az egyes szerkezeti elemek esetében a ciklikus terhelés során tapasztalható degradációt figyelembe vegyük: számításainkban feltételeztük, hogy a fix saru viselkedése ideális rugalmas-képlékeny felkeményedő anyagmodellel leírható (nincs degradáció), a vasbeton pillér esetében viszont a teherbírásban bizonyos degradáció tapasztalható. Felhívjuk a figyelmet, hogy megfelelő vasalás nélkül a viselkedés sokkal kedvezőtlenebb.
Az eredmények azt mutatják, hogy a saruk nem-linearitása határozza meg a szerkezet globális nem-lineáris viselkedését: a pillérek képlékenyedése lényegesen magasabb szinten következne be, mint a saruk merevségének csökkenése. Az 5. ábra a lineáris és nem-lineáris time-history analízis főbb eredményeit hasonlítja össze. Mint látható, relatíve duktilis saru figyelembevétele jelentősen csökkenti az igénybevételeket, viszont a kialakuló elmozdulások megnövekednek. Ezek az eredmények előrevetítik a nem-lineáris, elmozdulás-függő csillapító eszközök (NLD) alkalmazhatóságát a földrengési terhek hatékony csökkentésére, melyre a következő fejezetekben mutatunk példát.
  |
Szeizmikus szigeteléscsillapítók alkalmazása
A következőkben egy négynyílású, nyílásonként 75 m támaszközű, acél szekrény felszerkezetű, folytatólagos közúti híd mintáján mutatjuk be a csillapítók segítségével kialakított szeizmikus szigetelés alkalmazhatóságát. A hídszerkezet kialakításában az előző példában bemutatotthoz hasonló; további részletekért lásd Martinovich (2012) diplomamunkáját.
Két alternatív megoldást dolgoztunk ki a szeizmikus állékonyság biztosítására:
- a. hagyományos saruk alkalmazásával, a felszerkezetet hosszirányban egy pilléren lekötve a szükséges pillér keresztmetszet és alapozás meghatározása kvázi-rugalmas viselkedést feltételezve;
- b. nem-lineáris elmozdulás-függő (NLD) csillapító alkalmazásával.
Az NLD csillapítók viselkedése a viszkózus csillapítókkal ellentétben nem a sebességtől, hanem a deformációktól függ. Az energiaelnyelő képességet jellemzően valamely szerkezeti elem (pl. duktilis acél elem) képlékenyedésével biztosítjuk. Ilyen eszközök hídszerkezetekben való alkalmazhatóságát vizsgálta Martinovich (2010) TDK munkájában.
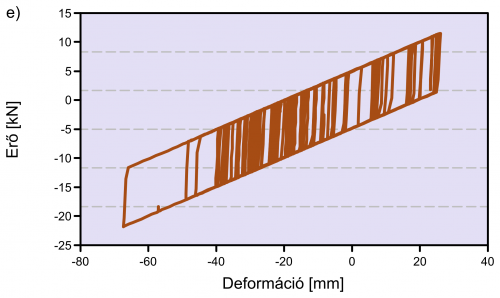
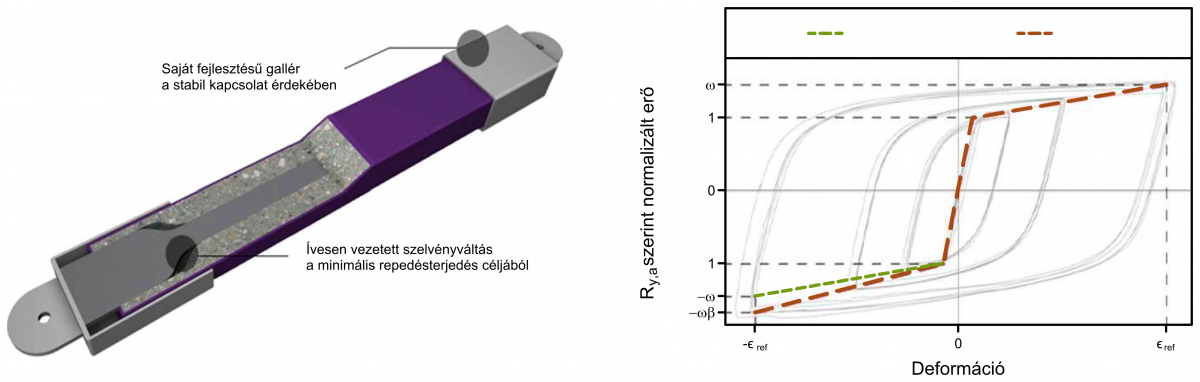
Egy ilyen, a magasépítésben már elterjedt eszköz a kihajlásbiztos merevítő rúd (buckling restrained brace, BRB) (Zsarnóczay, 2012), melynek hiszterézis viselkedésére mutat példát a 6. ábra (Zsarnóczay és Vigh, 2012). Az NLD eszközök viselkedése általában egy bilineáris karakterisztikával írható le; az itt ismertetett számításainkban a 7. ábrán közölt karakterisztikákat használtuk. Amennyiben a felszerkezet-pillér kapcsolatot hagyományos saruk helyett ilyen elemekkel alakítjuk ki, az elem képlékenyedése lehatárolja a felszerkezetről az alépítményre átadódó terheket, ezzel csökkentve a szeizmikus hatást. A csillapító elem képlékeny viselkedését jellemzően felkeményedés jellemzi, így az alépítményre átadódó erő az elem névleges teherbírásánál nagyobb lesz, mértéke függ a tényleges mechanikai jellemzőktől és a kialakuló képlékeny deformációktól (6–7. ábra).
Az ilyen kialakítással egy adott teherszint elérésekor kvázi elszigeteljük a felszerkezetet az alépítménytől; a módszert szeizmikus szigetelésnek, az alkalmazott csillapító elemet szigetelő elemnek hívjuk.
 |
 |
A hagyományos saruk alkalmazása esetén a földrengési analízis az előző pontban is bemutatott modális válaszspektrum analízis segítségével történhet. A csillapító esetében pontos eredményt a nem-lineáris time-history analízis adna, ugyanakkor a szerkezet közelítő méretezésére a modális válaszspektrum analízis is alkalmazható. Ekkor a BRB elemeket helyettesíthetjük ekvivalens rugókkal, ahol a rugómerevséget a kialakuló képlékeny elmozdulásokhoz tartozó effektív húrmerevséggel azonosnak vehetjük (7. ábra). A számításban ilyenkor a rugalmas válaszspektrumból kell kiindulni, de azt az effektív csillapításnak megfelelően lehet csökkenteni. A számítás iterációt igényel: a rugalmas válaszspektrum analízisből kapott elmozdulás és az ehhez tartozó, BRB karakterisztikáról leolvasott igénybevétel alapján új effektív merevséget és effektív csillapítást kell meghatározni és a számítást megismételni addig, amíg az effektív merevségben bekövetkező változás elfogadható mértékűre nem csökken.
A BRB elem teherbírását és hosszát a következő szempontok alapján határozhatjuk meg:
- a. A BRB teherbírást úgy vegyük fel, hogy a teherbírási határállapotban meghatározható igénybevételekre az elem rugalmas maradjon. Ha a BRB teherbírás ezt az igénybevételt felülről közelíti, akkor a hagyományos méretezés alapján tervezhető, vagy annál csak kis mértékben erősebb pillér keresztmetszet elégséges.
- b. A kialakuló deformációkat a BRB elem biztosítsa, azaz rendelkezzen kellő duktilitással.
A 8. ábra sematikusan mutatja a kapott két alternatív megoldást.
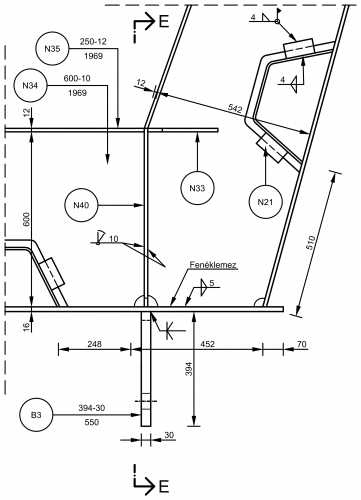
Az 1. változatban (8a. ábra) minden pilléren hosszirányban hagyományos mozgó sarut, egy pilléren pedig 2 db (sarunként egy), hosszirányban dolgozó, 260 kN névleges teherbírású, 5,5 m effektív hosszúságú elemet alkalmazunk. (Keresztirányban hagyományos sarut használunk.) A pillér-felszerkezet kapcsolat részletkialakítását mutatja a 9. ábra. Ekkor megtarthatjuk a teherbírási határállapotban meghatározott pillér keresztmetszeteket (1,4 m x 3,15 m). Az alkalmazandó cölöpalapozás: 4×6 = 24 db, 16 m hosszú, 80 cm átmérőjű CFA cölöp. A felszerkezet maximális hosszirányú elmozdulása 124 mm; a dilatációk kialakításával ekkora elmozdulási képességet kell biztosítani.
A 2. változatban (8b. ábra) a hagyományos pillér-felszerkezet fix saru kapcsolat megtartása mellett a pillért és az alapozást is jelentősen kell erősíteni. A pillér keresztmetszete: 1,9 m x 4,275 m, az alkalmazandó cölöpalapozás: 4×6 = 24 db, 22 m hosszú, 120 cm átmérőjű CFA cölöp.
Látható, hogy esetünkben a csillapító alkalmazásával jelentős költségcsökkentés érhető el.
  |

|
Utólagos megerősítés
Vizsgáljuk egy ötnyílású, nyílásonként 75 m támaszközű, acél szekrény felszerkezetű, folytatólagos közúti híd utólagos megerősítését. A szerkezet kialakítása az előzőekhez hasonlatos; további adatait lásd Dani (2010) diplomamunkájában.
A mintapéldában feltételezzük, hogy a teherbírási határállapotban méretezett szerkezet földrengésre nem felel meg: a hosszirányban fix támasznál a pillértő és az alapozás kihasználtsága rendre 220% és ~400%.
Vizsgáljuk az alábbi megerősítési módokat:
- hosszirányú fix támasz kialakítása több pilléren,
- pillér és alapozás megerősítése,
- csillapító eszköz alkalmazása.
A több pilléren kialakított fix támasz a szerkezet globális merevségét jelentősen megnöveli, melynek következtében a hosszirányú domináns lengésalak periódusideje lecsökken, a földrengésteher megnövekszik. Ezt a megnövekedett terhet ugyan több pillér veszi fel, esetünkben mégsem nyújt ez megoldást, mert a többi pillért korábban nem méretezték jelentős hosszirányú hatásokra. További problémát jelenthet a felszerkezet gátolt hőmérsékleti alakváltozásból fellépő, jelentős, a szeizmikus terhek nagyságrendjébe eső erők. A probléma feloldható a fix lekötéseket helyettesítő, lassú alakváltozásokat engedő dugattyús elemek alkalmazásával. Ezek az elemek azonban relatíve költségesek.
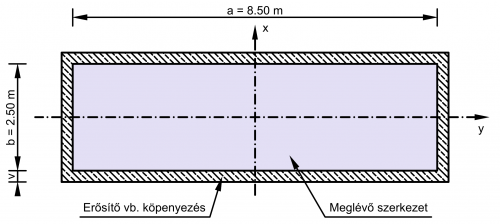
A második variáns szerint a pillér betonköpenyezéssel, az alapozás alácölöpözéssel megerősíthető. A vasbeton pillér teherbírásának biztosítására 40 cm széles betonköpeny alkalmazása indokolt (10. ábra). Az eredeti alapozás teherbírása messze elmarad a szükségestől. Az utólagos alapozás-megerősítés rendkívül költséges megoldás.
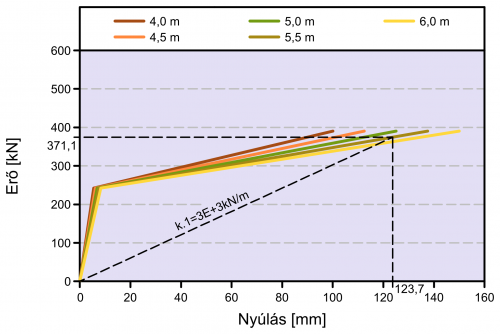
A harmadik variánsban a korábbiakban is bemutatott nem-lineáris csillapítóval felülről lehatárolhatjuk az alépítményre adódó terheket, így a meglévő pillérszerkezet és alapozás megerősítése nem szükséges. A pillér határerejére tervezett kapcsolatot 4 db, 10 cm2 magkeresztmetszetű (235 kN névleges teherbírású), 6,1 m hosszú (4 m hatékony hosszúságú) BRB elemmel alakíthatjuk ki (11. ábra). A kialakuló képlékeny deformációk kezelhető mértékűek.
Utóbbi megoldás minimális beavatkozást igénylő, költséghatékony megerősítési módnak bizonyul. Hangsúlyozzuk, hogy alkalmazhatóságának az elem deformációs képessége, valamint a kialakuló felszerkezet-elmozdulások mértéke szab határt. A piacon számos egyéb típusú, az adott feladathoz specifikusan illeszthető csillapító eszköz érhető el.
 |
 |
Összefoglaló megállapítások
Cikkünkben a szeizmikus hatásokra érzékeny hídszerkezetek állékonyságának biztosítására alkalmazható megoldásokkal foglalkoztunk, három esettanulmány ismertetésének segítségével. A bemutatott vizsgálatok az alábbi megállapításokat illusztrálják.
Hídjaink szeizmikus viselkedés szempontjából kritikus pontjai jellemzően a saruk, az alépítmények, az alapozás. A hagyományos módon – pusztán teherbírási határállapotra, a földrengési hatások elhanyagolásával – tervezett szerkezet földrengésre történő megerősítése szükséges lehet.
A modális válaszspektrum analízis jelentős mértékben túlbecsülheti a kialakuló földrengés terheket. A szeizmikus ellenállás ellenőrzése alapjául szolgáló számított hatások csökkenthetők fejlett analízis módszerek (lineáris vagy nem-lineáris dinamikai – time-history analízis) alkalmazásával. A szeizmikus ellenállás kihasználtságában akár 30-50% csökkentés is elérhető ilyen módon.
Amennyiben a kihasználtság ennél is nagyobb, a hagyományos megerősítési módok (pl. betonköpenyezés) mellett/helyett gazdaságos megoldást érhetünk el csillapítók, szeizmikus szigetelés alkalmazásával. Utólagos megerősítés esetén a beavatkozás mértéke is minimalizálható (pl. elkerülhető az alapozás megerősítése). A példák alátámasztják, hogy a hazai, moderált szeizmicitású környezetben is van létjogosultsága a csillapítók, speciális földrengésvédelmi eszközök alkalmazásának.
Hangsúlyozzuk, hogy bár példáinkban egy adott típusú, nem-lineáris elmozdulás-függő csillapító elemet alkalmaztunk, célunk csupán a földrengésvédelmi eszközök alkalmazhatóságának illusztrálása volt. Csillapítók, szeizmikus szigetelő eszközök rendkívül széles választéka érhető el a piacon, és az adott feladathoz specifikusan választhatjuk ki a legmegfelelőbb földrengésvédelmi eszközt.
Felhasznált irodalom
Dani B. (2010) Folytatólagos többtámaszú híd utólagos megerősítése földrengésre. Diplomamunka. BME Hidak és Szerkezetek Tanszék, Budapest.
Magyar Útügyi Társaság (2004) Útügyi Műszaki Előírás – ÚT 2-3.401 Közúti hidak tervezése, Általános előírások
MSZT (2008) MSZ EN 1998-1:2008 Eurocode 8: Tartószerkezetek tervezése földrengésre. 1. rész: Általános szabályok, szeizmikus hatások és az épületekre vonatkozó szabályok
MSZT (2006) MSZ EN 1998-2:2006 Eurocode 8: Tartószerkezetek tervezése földrengésre. 2. rész: Hidak
Martinovics K. (2010) Csillapító berendezések alkalmazása hazai gerendahidak szeizmikus méretezésében – Numerikus modellezés. TDK dolgozat. BME Hidak és Szerkezetek Tanszék.
Martinovich K. (2011) Többtámaszú folytatólagos gerendahíd tervezése földrengésre. BSc diplomamunka. BME Hidak és Szerkezetek Tanszék, Budapest.
Simon J. (2012) Numerical model development for seismic assessment of continuous girder bridges. Proc. Conf. of Junior Researchers in Civil Engineering, pp. 216-224. Budapest, Hungary.
Simon J., Vigh L. G. (2012) Seismic assessment of Hungarian highway bridges – A case study. Proc First Intl Conf PhD Students in Civil Engineering. Kolozsvár, Románia, 2012.11.04-2012.11.07. pp. 155-162.
Tóth L., Győri E., Mónus P., Zsíros T. (2006) Seismic Hazard in the Pannonian Region, In: The Adria Microplate: GPS Geodesy, Tectonics, and Hazards, Springer Verlag, NATO ARW Series, vol. 61, pp. 369-84
Vigh L. G., Dunai L., Kollár L. P. (2006) Numerical and design considerations of earthquake resistant design of two Danube bridges, Proc. First European Conference on Earthquake Engineering and Seismology, p10
Vigh L. G. (2012) Szeizmikus méretezési koncepció Magyarországon – Rugalmas méretezés vagy kapacitástervezés? Magyar Építőipar 2012/6, pp. 215-21
Ed. Vigh L. G. Rugalmas és disszipatív szeizmikus méretezési koncepció moderált szeizmicitású területen. Kutatási jelentés. BME Hidak és Szerkezetek Tanszék, Budapest (2012) (megjelenés alatt)
Zsarnóczay Á. (2010) Magyarországi típushidak szeizmikus viselkedése. Diplomamunka. BME Hidak és Szerkezetek Tanszék, p. 111
Zsarnóczay Á. (2012) Seismic Performance evaluation of buckling restrained braces and frame structures. Proc. 9th fib Intl PhD Symposium in Civil Engineering. Karlsruhe, Németország, 2012.07.22-2012.07.25. pp. 195-200.
Zsarnóczay Á., Vigh L. G. (2012) Kihajlásbiztos merevítőrudak kísérleti vizsgálata. Magyar Építőipar 2012/6, pp. 222-30.
Zsarnóczay Á., Vigh L. G., Kollár L. (2013) Magyarországi közúti gerendahidak szeizmikus viselkedésének vizsgálata. Magyar Építőipar 2013/2 (megjelenés alatt)