https://doi.org/10.36246/UL.2025.2.03
2025; 13. évfolyam, 22. szám
Pdf: Az EUROCODE szerinti forgalmi tehermodellek kialakulása, alkalmazása és kalibrációja WIM adatokkal
Bevezető
A harmonizált Eurocode-ok immár három évtizede a tartószerkezet méretezés alapvető dokumentumai Európában. A tartószerkezeti Eurocode-ok a magasépítésben már több, mint egy évtizede alkalmazott szabványok hazánkban is, azonban a hídépítés területén még nem kerültek teljes körűen bevezetésre. Az Útügyi Műszaki Előírások (UME) rendszere az Eurocode-tól eltérő méretezési előírásokat tartalmaznak, melyek a hidak tervezésének kötelezően alkalmazott de facto előírásai. Az UME-k felülvizsgálata folyamatban van, hogy az európai harmonizáció a hídépítés területén is végbe menjen. A jelenleg alkalmazott magyar hídterhelési osztályok is merőben különbözőek, mint az Eurocode tehermodelljei.
A Eurocode szerinti tehermodellek kalibrációja lehetséges a valós forgalmi adatokon alapuló eljárással. A kalibrációt a MSZ EN 1991-2 szabvány Nemzeti Mellékletében lehet meghatározni. A kalibrációhoz jó lehetőséget ad a mozgás közbeni tengelysúlymérés technológiája (Weight-In-Motion, rövidítve WIM). A technológia Magyarországon is ismert: az úthálózat védelmében bevezetett TSM hálózat is WIM szenzoros adatgyűjtés adatait alkalmazza.
Jelen cikkben az Eurocode tehermodelljeinek kialakulását, alkalmazását és kalibrációját tekintjük át nemzetközi összevetésben kitérve azokra a részletekre, melyeket a magyarországi bevezetés előtt szem előtt szükséges tartani.
Az Eurocode szerinti forgalmi terhek kialakulása
A tehermodell megalkotását megelőző mérések
Az EN 1991-2 szabvány megalkotásánál a cél egy olyan tehermodell meghatározása volt, amely (i) könnyen használható, (ii) statikai váztól függetlenül alkalmazható, (iii) az összes forgalmi szituációt leírja (haladó forgalom, forgalmi dugó, araszolás), (iv) tartalmazza a dinamikus hatást, (v) lokális és globális hatásokat is könnyen modellezhetővé tesz, (vi) egyértelmű [1]. Egy ilyen tehermodell kidolgozásához szükséges volt a valós forgalmi szituációkat leíró mérések elvégzése, melyekből levezethetőek azok a tehermodellek, amik reprezentálják a kontinens közúthálózatának és ezzel együtt a hídszerkezetek terhelését. Az alapvető problémát az jelentette, hogy pár napos/hetes adatok feldolgozásából kellett 100 éves élettartam alatt várható terheléseket extrapolálni.
A tehermodell megalkotásához kettő mérési kampányt hajtottak végre (i) 1977-1982 között Franciaországban, Németországban, Nagy-Britanniában, Olaszországban és Hollandiában, illetve (ii) 1984-1988 között számos európai úton. A programban 1000-8000 nehézgépjármű mérését hajtották végre az autópályákon és 600-1500 nehézgépjármű mérését a főutakon. A méréseket az 1950-es évektől ismert WIM (weight-in-motion) technológiával végezték el. A gyors sávokban és a másodrendű utakon mindössze 100-200 nehézgépjármű mérését tudták elvégezni. A mérési pontok közül az angliai adatok nem tükröztek megfelelő reprezentativitást, míg a spanyol és a holland adatok a különleges járművek túlzott hatása miatt vetettek el [1]. Összegezve: az analízisbe vett mérési pontok Auxerre (F) Garonor (F) Brohltal (D) Fiano Romano (I) Sasso Marconi (I) és Piacenza (I) voltak.
Az 1. táblázat a mért napi forgalmi adatokat mutatja be:
| személy gépjármű | nehézgépjármű | követés távolság
<100 m aránya |
|
| Brohltal (D) | 11126 | 4793 | 26,7 |
| Garonor (F) 1982 | – | 2570 | 32,6 |
| Garonor (F) 1984 | – | 3686 | 32,3 |
| Auxerre (F) lassú sáv | 8158 | 2630 | 18 |
| Auxerre (F) gyors sáv | 1664 | 153 | 8,5 |
| Fiano Romano (I) | 8500 | 4000 | 26,1 |
| Piacenza (I) | 8500 | 5000 | 30,9 |
| Sasso Marconi (I) | 7500 | 3500 | 24,3 |
A 2. táblázatban a nehézgépjárművek mérési adatokban felmért összetételének %-os megoszlását adtuk meg az [1] szerint.
| 2 tengelyes nehézgépjármű (%) | 2-nél több tengelyes nehézgépjármű (%) | csuklós tehergépjárművek (%) | pótkocsis teherautók (%) | |
| Brohltal (D) | 16,6 | 1,6 | 40,2 | 41,6 |
| Garonor (F) 1982 | 38,6 | 2,6 | 47,6 | 11,2 |
| Garonor (F) 1984 | 47,5 | 2,2 | 44,3 | 6,0 |
| Auxerre (F)
lassú sáv |
22,7 | 1,3 | 65,2 | 10,8 |
| Auxerre (F)
gyors sáv |
27,6 | 3,5 | 58,4 | 10,5 |
| Fiano Romano (I) | 41,4 | 7,0 | 29,0 | 22,6 |
| Piacenza (I) | 35,3 | 7,5 | 35,8 | 21,4 |
| Sasso Marconi (I) | 40,1 | 10,0 | 30,2 | 19,7 |
Általánosságban elmondható, hogy az európai forgalmi adatok elemzése azt mutatja, hogy a nehéz járművek tengelyterhelésének és össztömegének átlagértékei erősen függenek a forgalom típusától, azaz az utak osztályozásától, és általában nagyon széttartóak (3. táblázat):
- A tengelyterhelés statisztikai eloszlása általában egyváltozós, a módusz körülbelül 60 kN, míg a teljes tömeg statisztikai eloszlása kétváltozós, az első módusz körülbelül 150 kN, a második módusz körülbelül 400 kN.
- A napi maximális értékek sokkal kevésbé érzékenyek a forgalom típusára. 130 kN és 210 kN között változnak szóló tengelyek esetében, 240 kN és 340 kN között kéttengelyes járművek esetében, 220 és 390 kN között háromtengelyes járművek esetében, valamint 400 és 650 kN között a teljes tömeg tekintetében.
- Tapasztalat volt, hogy a tengelyterhelés napi maximuma, valamint a jármű teljes tömegének napi maximuma jelentősen meghaladja a jogilag megengedett értékeket.
- A teherautógyártók 1980 óta nagyon hasonló tengelyelrendezésű gépjárműveket és vontatmányokat gyártanak: három jól elkülöníthető tengelycsoport különböztethető meg: (i) a két- és háromtengelyes csoport tengelytávja 1,30 m (a pótkocsik és vontatmányok tengelycsoportja), (ii) a vontatók tengelytávja jellemzően 3,20 m távolsággal jellemezhető, míg (iii) a kéttengelyes nehézgépjárművek 5,40 m-es tengelytávval jellemezhetőek, bár ez az érték sokkal jobban szór.
- Az európai távolsági forgalom adatai kellően homogén értékeket eredményeztek.
- A nehéz járművek összetétele az 1980-as években átalakult: a nyerges vontatók aránya nőtt, amellett, hogy a kevésbé jövedelmező pótkocsival rendelkező teherautók száma jelentősen csökkent, és egyidejűleg csökkent az egytengelyes teherautók száma is, amelyek használata egyre inkább a helyi útvonalakra korlátozódott.
- A tehergépjármű-flották jobb és ésszerűbb logisztikája következtében csökkent vagy korlátozódott az üres tehergépjárművek közlekedtetésének száma, így növelve az átlagos járműterhelést.
- A távolsági forgalom sokkal nagyobb terhelési intenzitást jelent, mint a helyi forgalom.
- Általában a tehergépjármű-forgalom növekedő tendenciát mutat (megjegyzés: a tanulmányokban az abszolút maximumot (napi 8600 tehergépjármű autópályán a lassú sávban) 1980-ban Németországban, a Limburger Bahn-on rögzítették).
A fenti megfontolások alapján a modell kalibrálása céljából úgy döntöttek, hogy homogén referenciaforgalomként a Franciaországban, az A6-os autópályán Auxerre közelében rögzített adatokat választják. Az auxerre-i forgalom nagyon intenzív, és hatékonyan bemutatja a hosszú távú európai forgalom főbb jellemzőit, különösen összetételét tekintve. A többi forgalmi adatot csak az Auxerre-ben kapott eredmények megbízhatóságának ellenőrzésére használták [1].
A tehermodell megalkotása tehát a ma rendelkezésre álló adatok töredékéből lett meghatározva, hiszen csupán egyetlen helyszín mérési adataiból kalibrálták.
| összes tengely | ikertengely | hármas tengely | ||||||||||
| db | Pmean (kN) | σ (kN) | Pmax (kN) | db | Pmean (kN) | σ (kN) | Pmax (kN) | db | Pmean (kN) | σ (kN) | Pmax (kN) | |
| Brohltal (D) | 19970 | 59,0 | 28,4 | 165,0 | 1977 | 116,5 | 54,6 | 260,0 | 1035 | 60,0 | 230,0 | 355,0 |
| Garonor (F) 1982 | 8470 | 57,6 | 27,6 | 180,0 | 712 | 126,3 | 49,3 | 340,0 | 303 | 90,0 | 200,0 | 295,0 |
| Garonor (F) 1984 | 11593 | 59,3 | 30,0 | 195,0 | 1016 | 132,1 | 58,1 | 290,0 | 489 | 90,0 | 200,0 | 320,0 |
| Auxerre (F) lassú sáv | 10442 | 82,5 | 35,2 | 195,0 | 844 | 165,6 | 54,0 | 305,0 | 961 | 130,0 | 250,0 | 390,0 |
| Auxerre (F) gyors sáv | 581 | 73,1 | 41,2 | 200,0 | 47 | 141,2 | 63,9 | 275,0 | 51 | 12,0 | 250,0 | 390,0 |
| Fiano Romano (I) | 15000 | 56,8 | 32,9 | 142,0 | 2000 | 115,2 | 45,5 | 245,0 | 900 | 80,0 | 260,0 | 360,0 |
| Piacenza (I) | 20000 | 61,8 | 31,0 | 135,0 | 2500 | 127,0 | 44,1 | 260,0 | 1500 | 100,0 | 220,0 | 365,0 |
| Sasso Marconi (I) | 13000 | 61,9 | 30,8 | 135,0 | 1600 | 136,4 | 49,5 | 260,0 | 800 | 110,0 | 250,0 | 375,0 |
Az Eurocode szerinti tehermodellek
Az 1. tehermodell – LM1
Az LM1 (1. ábra) egy folyamatos, forgalmi akadályok vagy torlódások közepette haladó forgalmat ír le, amelyben nagyrészt nehézgépjárművek vesznek részt. Az 1. tehermodell két elemből tevődik össze. A koncentrált teher, amelyet ikertengelyek reprezentálnak, valamint felületen megoszló terhelés.
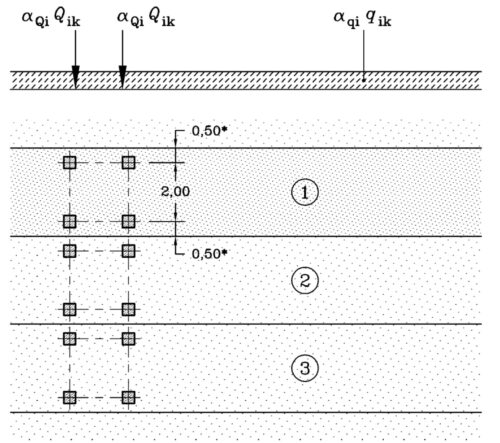 |
Az 1. tehermodell (LM1) alkalmazása
Jelmagyarázat:
(1) 1. sáv: Q1k = 300 kN; q1k = 9,0 kN/m2
(2) 2. sáv: Q2k = 200 kN; q2k = 2,5 kN/m2
(3) 3. sáv: Q3k = 100 kN; q3k = 2,5 kN/m2
* wl = 3,00 m esetén
A tengelyterheket (TS) a következő képlettel lehet meghatározni:
αQiQik
ahol:
αQi: a terhelési osztályba sorolási tényező az i-edik sávban
Qik: a koncentrált ikertengely tengelyterhelésének karakterisztikus értéke az i-edik sávban
A megoszló terheket (UDL) a következő képlettel lehet meghatározni:
αqiqik
ahol:
αqi: a terhelési osztályba sorolási tényező az i-edik sávban
qik: az egyidejű megoszló terhelés karakterisztikus értéke az i-edik sávban
Az αQ és αq tényezőket 0,8-nál nagyobb értékre lehet felvenni. A pontos értéket az Eurocode Nemzeti Melléklete szabályozza. Az αQ=1,0 és αq=1,0 értékek a nagyterhelésű, nemzetközi tranzitforgalmat leíró, nagyrészt totális leterheléssel üzemelő hidak terhelését reprezentálja. A dinamikus hatást a tehermodell tartalmazza, külön tényezővel való szorzás nem szükséges.
A 2. generációs Eurocode az előírásokon nem változtatott, az LM1 tehermodell leírása megegyezik az 1. generációs tehermodellel.
A 2. tehermodell – LM2
Az LM2 (2. ábra) egyetlen tengelyen működő βQQak nagyságú teher. A Qak értéke: 400 kN. Ez a terhelés szintén tartalmazza a dinamikus terhelést és az útpályán bárhol elhelyezkedhet. Az LM2 tehermodell általában lokális vizsgálatoknál és kis fesztávú hidaknál lehet mértékadó. A βQ értéke megegyezik αq1 értékével.
 |
A 3. tehermodell – LM3
Különleges járműveket leíró tehermodellek. Ezek a tehermodellek a kezelői, beruházói, valamint a katonai mobilitási igények esetén kerülnek vizsgálatra. Általános esetben nem szükséges a vizsgálatuk, azonban amennyiben vizsgálni szükséges, akkor egyes esetekben mértékadó terheléseket jelenthetnek.
A 4. tehermodell – LM4
Az embertömegből származó teher, mely jelen vizsgálatoknak nem tárgya.
Az első magyar Nemzeti Melléklet terhelési osztályba sorolási tényezői
Az Eurocode-ok hazai bevezetése előtti időszakban világossá vált, hogy a korábbi magyar szabványok több esetben alacsonyabb biztonsági szintet eredményeztek, ezért szükségessé vált a teljes tehermeghatározási és parciális tényezős rendszer részletes újraértékelése. A történeti összehasonlítások rámutattak, hogy a magyar előírások mind magasépítésben, mind hídépítésben kisebb teher- és anyagoldali parciális tényezőket alkalmaztak, ami a tényleges megbízhatósági szint elmaradását okozta az Eurocode-okhoz képest [3].
A hidakra javasolt α-tényezők kalibrálása során figyelembe vették a hazai forgalmi viszonyokat, a járműállomány jellegét, a magyarországi terhelési spektrumot, valamint azt, hogy a nagyobb terhelési osztályba sorolási tényezők összességében csak minimális beruházási többletet, ugyanakkor jelentős fenntartási és tartóssági előnyt jelentenek. A módosított αQi és αqi értékeket úgy választották meg, hogy a magyar Nemzeti Melléklet a tényleges hazai terhelési környezetre legyen kalibrálva – akként, hogy a gyakorlatban mai napig alkalmazott ÚME A osztályú járműterhével [4] hasonló igénybevételszintet eredményezzen –, miközben teljesíti az Eurocode által előírt megbízhatósági szintet és összhangban áll az európai felelősségi- és biztosítási elvárásokkal: két terhelési osztályt határoztak meg, az eredeti értékeket a 4. táblázat mutatja be [5].
| αQ1 | αQ2 | αQ3 | αq1 | αq2 | αq3 = αqr | |
| Eredeti EC1-2 „nehéz forgalom” | 1,0 | 1,0 | 1,0 | 1,0 | 1,0 | 1,0 |
| NA I. terhelési osztály | 1,0 | 0,8 | 0,0 | 0,8 | 1,0 | 1,0 |
| NA II. terhelési osztály | 0,8 | 0,8 | 0,0 | 0,6 | 1,0 | 1,0 |
A legtöbb európai ország az Eurocode ajánlásának megfelelően αQi=1,0 és αqi=1,0 értékben választotta meg a nagyterhelésű úthálózatának terhelési osztályba sorolási tényezőit, alsóbbrendű utakra pedig csökkentette azok értékeit [6].
Korai kalibrációs eljárások
Németországi tehermodell kalibráció
Az Eurocode forgalmi tehermodelljeinek alkalmazása során már a kezdetektől felmerült az igény a nemzeti viszonyokhoz igazított kalibrációra. Németországban a Bundesanstalt für Straßenwesen (BASt) végezte el az első átfogó vizsgálatokat annak érdekében, hogy a közúti forgalmi hatások alapján meghatározhatók legyenek az LM1 tehermodellhez tartozó α-terhelési szorzók. A cél az volt, hogy a tehermodellek valós forgalmi hatásokat tükrözzenek, figyelembe véve a 2000-es évekre jellemző, gyorsan növekvő nehézgépjármű-forgalmat. A kalibráció alapját az 1980-as évektől működő forgalommérő állomások, illetve a később telepített WIM rendszerek adatai képezték [7].
A német vizsgálatok módszertana az aktuális és jövőbeli forgalom szimulációjára épült. A WIM-adatokból származó, tengelyterhelésre, járműtípusra és járműkövetési távolságra vonatkozó eloszlásokat Monte Carlo szimulációkkal generálták újra, így modellezték a különböző forgalmi helyzetket. A szimulációk során többféle nehézjármű-változatot vettek figyelembe, amelyek a jelenlegi, illetve prognosztizált jövőbeli forgalmat különböző intenzitásokkal és tengelykonfigurációkkal reprezentálták – például 60 tonnás moduláris járműveket vagy 65 tonnás, hat tengelyes szerelvényeket is [7].
A forgalmi hatások meghatározása különböző hídszerkezet típusokon (vasbeton és acél gerendahidak különböző keresztmetszetekkel, mint lemezhidak, szekrénykeresztmetszetek, valamint előregyártott elemes hidak) történt. Az egyes szerkezetekre jellemző igénybevételeket a járműforgalomból származó terhelési időfüggvények alapján határozták meg, majd statisztikai módszerekkel vizsgálták azok eloszlását. A jellemző értékeket 1000 éves visszatérési periódusra definiálták, ami a szabványban is alkalmazott biztonsági szinttel volt összhangban [7].
A mérések helyszíneit a német autópálya-hálózat különböző pontjain választották ki oly módon, hogy reprezentálják a nehézjármű-forgalom területi sajátosságait – az ipari központok, határátkelők és nagy tranzitforgalmat bonyolító szakaszok terhelési viszonyait egyaránt. A WIM-mérések eredményeiből országos forgalmi szinteket és trendeket határoztak meg, amelyekből különböző jövőbeli forgalmi eseteket extrapoláltak. A jövőbeli növekedést gazdasági prognózisokra, a szállítási volumen várható emelkedésére és a 40 tonnás járművek elterjedésére alapozták.
A szimulációk eredményeit az EN 1991-2 szerinti LM1 tehermodellel vetették össze. Az összehasonlítás kimutatta, hogy a korabeli LM1 jól reprezentálta a németországi aktuális forgalmi hatásokat, azonban a jövőbeni terhelési szintek várhatóan meghaladják annak szintjét. Ezért egy módosított LM1 (LMM1) modellt javasoltak, amely az LM1 felső burkológörbéjeként szolgált, és megfelelő biztonsággal lefedte a 2020-2030-as időszakra becsült forgalmi terheléseket. A BASt vizsgálat ezen eredmények alapján javasolta az αQi és αqi korrekciós tényezők új, nemzeti értékeinek meghatározását a német Nemzeti Mellékletben [7].
A német kutatási programot később az osztrák és svájci hatóságok is alapul vették. Svájcban az ASTRA 82001 jelentés (első kiadása 2006, legutóbbi frissítése 2025) a BASt-módszertanra építve fejlesztette tovább a kalibrációt, immár kiterjedt WIM-adatbázisra és korszerű statisztikai eszközökre támaszkodva [8]. A svájci eljárás célja az LM1-hez kapcsolódó αact („aktualizált”) tényezők meghatározása volt a SIA 261 és SIA 269/1 szabványokhoz. Az országos WIM-hálózat több pontján (pl. Denges, Mattstetten, St-Maurice) gyűjtött adatok alapján szimulálták a forgalmi sávonkénti járműeloszlást, tengelykonfigurációkat és járműkövetési távolságokat. Ausztria bevezette a németországival azonos, az alapértékeknél magasabb αQi és αqi korrekciós tényezőket a vonatkozó Eurocode Nemzeti Mellékletében.
A svájci módszertan újdonsága a probabilisztikus extrapoláció volt, amely a forgalmi hatásokat 2050-ig terjedő időhorizonton értékelte, a megbízhatósági index (β) célértékeihez illesztve. A WIM-adatokból származó jellemző maximumokat Gumbel-eloszlások illesztésével határozták meg, majd a Block-Maxima módszerrel számították az αQ1,act és αq,act tényezőket. Az így kapott α-tényezők a német eredményekhez hasonlóan szakasz- és szerkezettípus-függőek, de a svájci forgalmi mintázatokhoz igazítottak [8]. Ezt az alkalmazást részletesen az 5.1. fejezetben külön is tárgyaljuk.
Összességében a német és svájci kalibrációs kutatások alapozták meg az Eurocode forgalmi tehermodelljeinek regionális adaptációját. Az eljárások közös jellemzője a WIM-adatokra épülő sztochasztikus forgalommodellezés, a több forgalmi sáv és szerkezettípus párhuzamos vizsgálata, valamint az α-tényezők kalibrálása 1000 éves visszatérési periódusú igénybevételi szintekhez. Ezek az elemzések biztosították, hogy a DACH-országokban alkalmazott Eurocode tehermodellek egységes megbízhatósági szinten tükrözzék a valós forgalmi hatásokat.
Forgalmi terhelések mérése statikus módszerekkel
A forgalmi terhelések közvetlen mérésének egyik legkorábbi, rendszerezett módszertani alapját az Egyesült Királyság Nemzetközi Fejlesztési Minisztériuma (DFID) által megrendelt Overseas Road Note 40 (ORN 40) dokumentum jelentette, amelyet a Transport Research Laboratory (TRL) készített el. Az első változat még 1978-ban jelent meg Road Note 40: A guide to the measurement of axle loads in developing countries using a portable weighbridge címmel, kimondottan a fejlődő országok számára, ahol az útpályaszerkezetek és hidak terhelési adatainak gyűjtése korlátozott volt. A 2004-ben kiadott frissített verzió már A guide to axle load surveys and traffic counts for determining traffic loading on pavements címmel jelent meg [9]. Ez az útmutató a fejlődő országok közúti infrastruktúrájának fejlesztését támogatta, részletes eljárásokat adva a forgalmi terhelések mérésére és kiértékelésére. Az ORN 40 nem szabvány, hanem ajánlás jellegű technikai kézikönyv, amely lényegében a nyers terhelési adatok megbízható előállítását szolgálja a pályaszerkezet- és hídszámításokhoz, különösen olyan országokban, ahol a korszerű automatikus rendszerek (pl. WIM) még nem álltak rendelkezésre.
Az egyik legkorábban alkalmazott eljárás az állandó mérőhidak (3. ábra) telepítése volt, beépített mérőállomásként funkcionálnak. Ezek a berendezések jellemzően forgalmas főutak mentén, fix beton alapra telepített acél hídmérlegekből állnak, melyek a jármű teljes tömegét és tengelyenkénti terhelését is képesek mérni. A módszer nagy pontosságú, mivel a járművet a méréshez teljesen meg kell állítani, és a terhelés egyensúlyi állapotban rögzíthető. A rendszer előnye a magas mérési pontosság és az állandó kalibráltság, hátránya viszont a korlátozott adatgyűjtési kapacitás és a magas beruházási költség. Ezen okokból ezek az állomások elsősorban hosszú távú forgalmi megfigyelésekhez, jogi ellenőrzésekhez és szabályozási célú súlyellenőrzéshez javasoltak, nem pedig nagy mennyiségű statisztikai adatgyűjtéshez [9].
 |
A hordozható mérőpadok (4. ábra) rugalmasabb mérési lehetőséget biztosítanak, mivel ezek szállítható, statikus tengelyterhelés-mérő eszközök. Ezek könnyen telepíthetők bármely megfelelően sík útszakaszon, és a járművek egyes tengelyei egymás után gördülnek rájuk, rövid megállásokkal. A mérést rendszerint kézi adatfelvétel kíséri (járműazonosítás, tengelytípus, abroncselrendezés). A rendszer fő előnye a mobilitás és a gyors telepíthetőség, így alkalmasak rövid távú forgalmi felmérésekre, ahol a cél a reprezentatív mintavétel, nem pedig folyamatos ellenőrzés. Ugyanakkor a mérési pontosságot befolyásolja a járművezető viselkedése, a pad helyes elhelyezése és a terepi körülmények (pl. útburkolat egyenetlensége, hőmérséklet), ezért a kapott adatokat statisztikai korrekciós eljárásokkal javasolt kiértékelni [9].
 |
A manapság leginkább elterjedt WIM rendszer, a korábbi statikus eljárások továbbfejlesztett, automatizált változata. A WIM érzékelők a burkolatba vannak beépítve, és a járművek mozgás közbeni tengelyterhelését mérik, így az adatgyűjtés folyamatos, a forgalom akadályozása nélkül történik. Míg a statikus mérések a pontosság és kalibrálás szempontjából nélkülözhetetlenek, a WIM előnye a nagy mintaszám és időbeli reprezentativitás, így ezen rendszerek egymást is kiegészíthetik. A WIM a leginkább alkalmas a hídterhelések valószínűségi eloszlásának és a forgalomdinamika hatásainak vizsgálatára, míg a statikus eljárások az alapkalibrációhoz és referencia-adatokhoz nyújtanak megbízható kiindulást [9].
A Weight-In-Motion (WIM) technológia alkalmazása hidak forgalmi terheléseinek meghatározására
A Weigh-In-Motion (WIM) technológia a közúti és vasúti járművek dinamikus tömegének és tengelyterhelésének meghatározására szolgáló mérési módszer, amely lehetővé teszi a járművek súlyának meghatározását a forgalom akadályozása nélkül. A WIM-rendszerek a mozgó járművek által kifejtett dinamikus kerékterheléseket mérik, és ezek alapján becsülik meg a statikus értékeket, így biztosítva a valós forgalmi terhelések kvantitatív leírását. A technológia a közúti infrastruktúra fenntartásának, a teherforgalom-szabályozásnak és a hídmenedzsment-rendszereknek (BMS) egyaránt nélkülözhetetlen adatforrásává vált [10], [11].
A WIM rendszerek többféle kialakításban alkalmazhatók: a low-speed WIM (LS-WIM) rendszerek ellenőrzött körülmények között, alacsony sebességnél működnek, míg a high-speed WIM (HS-WIM) rendszerek a nyílt forgalomban, normál sebességen végzik a mérést. Különleges változat a bridge-WIM (B-WIM), amelynél a szenzorokat a híd alsó szerkezeti elemeire rögzítik, és a járművek által okozott feszültségváltozásokból következtetnek a terhelésre. Ezenkívül az on-board WIM (OBW) rendszerek a járművekre szerelt szenzorok segítségével végzik a folyamatos súlymérést, míg a stress-in-motion (SIM) technológia a gumiabroncs-út kapcsolat többdimenziós feszültségállapotát is képes rögzíteni. A mérések pontossága a rendszer típusától függően ±1-10% között változhat [10].
A WIM technológia alkalmazási területei rendkívül szélesek. Az egyik legfontosabb felhasználási irány a pályaszerkezetek és hidak tervezése, illetve fenntartása, ahol a WIM adatok pontos képet adnak a valós forgalmi terhelésekről, így javítva a méretezési eljárások és élettartam-modellek megbízhatóságát. Továbbá a súlyellenőrzési és túlsúly-ellenőrzési célú alkalmazások révén a WIM rendszerek hozzájárulnak az úthálózat élettartamának meghosszabbításához, a szabályszegések visszaszorításához és a közlekedésbiztonság növeléséhez. A súlyalapú útdíjrendszerek esetében a WIM technológia a „szennyező fizet” elv érvényesítését teszi lehetővé, míg az ipari logisztikai központokban és kikötőkben a járművek túlterhelésének megelőzésére és árumérlegelésre használják.
A Bridge Management in Europe (BRIME) projekt eredményei kiemelik, hogy a WIM adatok integrálása a hídmenedzsment-rendszerekbe (BMS) jelentősen javítja a szerkezetek állapotfelmérését és a karbantartási döntéshozatalt. A hidak teherbírásának, romlási ütemének és szerkezeti viselkedésének modellezése során a WIM technológia valós, helyspecifikus terhelési adatokat biztosít, amelyek révén pontosabban meghatározható a szerkezet maradó élettartama és biztonsági szintje. A BRIME kutatás szerint a hídkezelésben alkalmazott adatvezérelt megközelítések – például a dinamikus terhelések figyelembevétele a megbízhatósági alapú értékelésekben – kulcsszerepet játszanak a karbantartási stratégiák optimalizálásában és a hosszú távú költséghatékonyság biztosításában [11]. A WIM technológia részletes bemutatása és alkalmazásának lehetőségeit részletesen elemzi a munkabizottság bevezető résztanulmánya [12].
Összességében a WIM technológia nemcsak a közúti hálózatok műszaki és gazdasági fenntartásához nyújt megbízható adatokat, hanem lehetőséget teremt a hidak valós idejű szerkezeti diagnosztikájára és terhelésfüggő monitoringjára is. Az automatizált adatgyűjtés és -feldolgozás révén a WIM rendszerek elősegítik a fenntartható infrastruktúra-gazdálkodást, támogatják az európai közlekedési hálózat egységesítését, és hozzájárulnak a biztonságosabb, költséghatékonyabb közlekedési rendszer megvalósításához [10], [11], [13], [14], [15], [16], [17].
Mérési adatok alapján meghatározott tehermodellek Európában a tranzitúthálózaton – Aktuális kutatások esettanulmányai I.
Svájci kutatási eredmények
Svájcban a közúti hidak teherbírásának és a forgalmi tehermodelleknek a kalibrációja az ASTRA (Bundesamt für Strassen) koordinálásában zajlik, a SIA 261 és SIA 269 szabványokhoz illeszkedve. Az ország a 2000-es évektől kezdődően építette ki WIM mérőállomás-hálózatát, amely jelenleg több mint tizenöt autópálya szakaszon gyűjt adatokat, többek között Gotthard, Denges, Oberbüren, Ceneri, Bozberg, St. Prex, Grauholz, Effretikon és Bad Ragaz állomásokon [8]. A WIM-adatgyűjtés 1999-ben indult, és azóta folyamatosan zajlik, így az ország Európában az egyik leghosszabb, több évtizedre visszanyúló adatbázissal rendelkezik. A mérések célja az volt, hogy a korábbi német kalibrációs módszereket (BASt B77) továbbfejlesztve, a svájci forgalmi viszonyokra jellemző α-tényezőket határozzák meg, az LM1 modell újrahangolásával, a probabilisztikus tehermodell alkalmazásával [18].
A mérési program több fázisban zajlott: az első 2005-ös vizsgálat [15] a svájci autópálya-hálózat reprezentatív szakaszait lefedve 15 éves időhorizontú előrejelzést készített, majd a 2014-es és 2025-ös felülvizsgálatok során a méréseket és az α-tényezőket aktualizálták. A svájci WIM-rendszer minden 3,5 tonnánál nagyobb járművet regisztrál, a Kistler M660 érzékelőkkel, 5-10%-os mérési pontossággal. Az éves kalibráció során kb. 45 tehergépkocsi statikus súlyát hasonlítják össze a WIM-adatokkal, újabban pedig „egyszerűsített kalibrációs eljárást” is alkalmaznak, mindössze három járművel, a forgalom megállítása nélkül [8]. Az adatok statisztikai eloszlását normalizált hibaintervallumok (±2-10%) és megbízhatósági szintek (90-95%) alapján osztályozzák, és minden állomásra külön pontossági osztályt rendelnek. A mintavételi helyszíneket forgalmi jelleg szerint választották ki: Gotthard és Ceneri az alpi tranzitforgalmat, míg Denges és Oberbüren az országos, főként belföldi forgalmat reprezentálta.
A forgalmi szimulációkat az AGB 2002/005 módszerével végezték, amely a „stationary traffic” állapotot (torlódott forgalom, 2%-os időarány) tekinti döntő teherállapotnak. A 2025-ös ASTRA 82001 jelentésben már több forgalmi szcenáriót – folyó, lassuló és torlódott forgalmat – is modelleztek, és a járműeloszlásokat a 2003-as és 2019-es mérések összevetésével validálták. Az adatok azt mutatták, hogy a svájci alagútforgalomban (pl. Gotthard, Ceneri) a nehéztehergépkocsik aránya 10-12%, míg az országos átlag 5-8% között alakult, ami tükrözi az alpesi vasúti teherforgalom erősödését és a közúti terhelések stabilizálódását [15].
A kalibrációs eredmények szerint a svájci SIA 261:2020 szabványban az αQi, αqi és αqr tényezők 0,90 értéken maradtak, ami 10%-kal kisebb teherintenzitást jelent az Eurocode LM1-hez képest. Az értékek mögött az a megfontolás áll, hogy a svájci teherforgalom intenzitása és a járművek súlyeloszlása tartósan alacsonyabb a nyugat-európai (német, francia) mintáknál, miközben a 40 tonnás járműtömeg-limit és a szigorú ellenőrzési rendszer stabilizálta a terhelési statisztikákat. A vizsgálatok nem különítettek el útkategóriákat vagy szerkezettípusokat, az a-értékek országos szinten egységesek, de jövőbeli frissítések során az alagutak és nagyfesztávú hidak esetében külön kategóriák bevezetése indokolt lehet [18]. A módszertan alapvetően nem extrapolál időben, hanem a legutóbbi 5-10 év WIM-adatain alapuló időstabil statisztikai kiértékelést alkalmaz, amely a jövőbeli forgalomnövekedést nem beépített feltételezésekkel, hanem újramérésekkel követi nyomon.
Olaszországi kutatási eredmények
Olaszországban számos, a második világháború után épült híd mára elérte vagy meghaladta tervezett élettartamát, azonban az újjáépítéshez és felülvizsgálathoz rendelkezésre álló források korlátozottak. A pontos, helyi viszonyokra szabott forgalmi modellek ezért alapvető fontosságúak a szerkezetek megbízható értékeléséhez és a karbantartási feladatok meghatározásához.
Az Eurocode LM1 terhelési modellje elsősorban autópályákra készült, és túl konzervatív eredményeket ad, ha kisebb forgalmú tartományi utakra alkalmazzák [19]. Ez a modell nem veszi figyelembe a járműtömegek, a forgalmi összetétel és az áramlási jellemzők regionális eltéréseit. A kutatás célja ezért egy valószínűségi alapú forgalmi modell létrehozása volt, amelyet WIM adatok felhasználásával kalibráltak három pisai tartományi úton: a La Botte-hídon (SP1), az Arno-hídon (SP66) és a Canale Imperiale-hídon (SRT206).
A kutatás egy ötlépéses módszertant követett:
- Adatgyűjtés WIM rendszerekkel, melyek tengelyterheléseket, tengelytávolságokat, sebességeket és járműközöket rögzítettek, 12 járműkategóriába sorolva a méréseket.
- Adattisztítás és statisztikai illesztés, amely során eltávolították a kiugró értékeket és valószínűségi sűrűségfüggvényeket illesztettek a fő forgalmi paraméterekhez.
- Forgalmi áramlás modellezése, ahol Monte Carlo szimulációval generáltak egyéves forgalmi sorozatokat, megkülönböztetve a folyó és torlódott forgalmi állapotokat a Greenshield-modell alapján.
- Éves maximális hatások becslése, amikor a szimulált forgalmat egyszerű kéttámaszú hídszerkezetek hajlítónyomaték- és nyíróerő-igénybevételeinek hatásábráira vetítették.
- Korrekciós tényezők kalibrálása, az Eurocode modell eredményeivel összevetve, legkisebb négyzetes illesztéssel.
A WIM mérések jelentős eltéréseket mutattak a tengelyterhelések és tengelytávolságok között, valamint kimutatták a túlterhelt járművek (akár 80 tonna) előfordulását is. A járműközök eloszlását külön vizsgálták szabad és torlódott forgalomban: előbbire lognormális, utóbbira negatív exponenciális keverék eloszlást alkalmaztak [19].
A Monte Carlo szimulációk 500 évnyi szintetikus forgalmi adatot generáltak, hogy meghatározzák az éves maximális terhelési hatásokat 10-50 méteres hídfelszerkezetekre. Az eredmények azt mutatták, hogy a javasolt modell szerinti hajlító- és nyíróerők jellemző értékei rendre alacsonyabbak, mint az Eurocode által előírtak, különösen hosszabb támaszközök esetén. Ennek oka, hogy a több nehézjármű egyidejű jelenlétének valószínűsége a kisebb forgalmú tartományi utakon lényegesen kisebb, mint autópályákon [19].
Az LM1 modellhez csökkentő α-tényezőket határoztak meg, hogy a terhelés a valós elővárosi forgalmi viszonyokat hűbben tükrözze. A fő forgalmi sávra az ikertengely terhelési tényező értéke 1,0 maradt, mivel a legnehezebb jármű továbbra is meghatározó rövid fesztávú hidaknál. Ugyanakkor az egyenletesen megoszló terhelési tényezője (αqi=1) 0,68-0,72 közé csökkent, amely a kisebb forgalmi sűrűséget és a ritkább többjárműves terhelést tükrözi. A másodlagos sávokra a koncentrált és megoszló terhelési tényezők rendre (αQi=2..i) 0,2-0,33, illetve (αqi=2..i) 0,36-0,50 közé estek [19].
A kalibrált terhelési modell lehetővé teszi a hídállomány hatékonyabb kezelését és reálisabb teherbírási értékelését, elkerülve a túlzott konzervativizmust. A jövőbeni olaszországi kutatások célul tűzték ki az országos úthálózati adatokra történő kiterjesztést [20].
Németországi újabb kutatási eredmények
A tehermodellek nemzeti szintű kalibrációja elsőként Németországban indult meg, ahol a szabványos Eurocode tehermodelleket a helyi forgalmi viszonyokhoz – a járműcsoportok összetételéhez és a forgalom intenzitásához – igazították [7]. Azóta is folyamatosan zajlik ezek finomítása, valamint új mérési és adatgyűjtési programok indítása.
Németországban kutatások folynak a Bridge-Weigh-in-Motion (BWIM) rendszerekben alkalmazott járműosztályozás pontosítása a forgalmi terhelések modellezésének javítása érdekében. A hagyományos BWIM-alkalmazások általában az egyszerű tengelykonfiguráció-alapú besorolást használják, amely azonban különböző tehergépkocsi típusokat egyetlen kategóriába sorol, így elmosva az eltérő szerkezeti és statisztikai jellemzőket. Ennek következtében a numerikus forgalmi szimulációkban alkalmazott paramétermodellek nem mindig tükrözik a valós tehereloszlást, különösen a hídszerkezet szempontjából kritikus járművek esetében.
Ennek figyelembevételére kidolgozásra került egy részletesebb osztályozási rendszer [21], [13], amely a járművek tengelytávolságát és teljes tengelysorhosszát is figyelembe veszi, lehetővé téve a különböző alaptípusok (például önjáró teherautó, félpótkocsi, vontatott pótkocsis jármű) megkülönböztetését azonos tengelyelrendezés mellett is. A vizsgálat alapját a németországi A92 autópályán gyűjtött, 2020. április-júniusi BWIM-adatok képezték. A kutatás két német osztályozású járműtípusra (112 jelű két szóló tengely és egy ikertengely, illetve 113 jelű két szóló tengely és egy hármas-tengely) fókuszált, amelyek a nagyobb tengelyszám és jellemzően nagyobb járműtömeg miatt a hídterhelés szempontjából a legjelentősebbek.
Az elemzés rávilágított, hogy még az azonos tengelykonfigurációba tartozó járművek között is jól elkülöníthető alosztályok figyelhetők meg a tengelysor hossza és az első tengelytávolság alapján. Ezek a különbségek a járművek tömegeloszlásában és tengelytávolsági statisztikáiban is megjelennek, ami a közúti terhek modellezésére is hatással van. Így egy részletesebb osztályozási táblázat került kidolgozásra, amely ezen alosztályokat külön kezeli, illetve meghatározták a hozzájuk tartozó valószínűségi eloszlásokat is (GVW, RAW, AS paraméterek).
A finomított osztályozás hatásait a terhelési hatások (nyomaték, nyíróerő) modellezésén keresztül vizsgálták különböző támaszközű egy- és kétnyílású tartók esetén. Az eredmények szerint az új besorolási rendszer jelentősen csökkenti a modellbizonytalanságot, különösen a rövid fesztávú hidaknál, ahol a járművek tengelyelrendezése és tehereloszlása nagyobb hatással van az igénybevételekre [13].
Finnországi kutatási eredmények
Finnországban a forgalmi tehermodellek kalibrációja az Eurocode bevezetését követően indult el, a Nemzeti Melléklet elkészítésével párhuzamosan. A cél az volt, hogy az LM1 tehermodellt a korábban használt finn nemzeti előírásokhoz igazítsák, majd a valós forgalmi adatok alapján újrakalibrálják [22]. A kezdeti α-tényezőket így először a korábbi szabványhoz illesztve határozták meg, nem pedig mért adatok alapján. 2013-2017 között indították el az első országos mérési programot, amely egy kiválasztott útszakaszon gyűjtött adatokat, és a járművek hosszát, tengelyszámát, tengelyelrendezését, tengelyterhelését és össztömegét regisztrálta [23]. A mérés ugyan nem volt országosan reprezentatív, de fontos lépést jelentett a jövőbeni WIM-alapú kalibráció irányába.
A mérési program 2013-ban egy 2007-es bázisállomás kalibrációjával indult, majd négy éven keresztül zajlott. Az adatokból jól látható volt, hogy a járművek össztömege folyamatosan növekszik, azonban ez nem járt együtt a tengelyterhelések arányos növekedésével – a nagyobb tömegek többtengelyes járművek megjelenésével oszlottak el a pályaszerkezeten. A vizsgálat alapján új járműkategóriákat vezettek be, amelyek jobban tükrözték a finnországi forgalmi összetételt, különösen a nagy terhelésű, többtengelyes kombinált járművek arányát [23].
2014 és 2018 között újabb, BWIM-méréseken alapuló terhelési program indult. A vizsgálat során 17 automatikus forgalomfigyelő pont és több BWIM-állomás adatait használták fel, köztük az Äänekoski, Kaarina, Olhava, Pirttikylä és Ring III helyszínekről. Az adatgyűjtés kombinálta a tengelytömeg-felméréseket és az automatizált forgalmi regisztrációkat, majd a forgalom statisztikai jellemzőit Monte Carlo szimulációval értékelték ki. A kalibrációs eljárás három lépésben zajlott: (i) szimuláció a 2013-as törvénymódosítás előtti adatokra, (ii) előrejelző modell kidolgozása a megnövekedett engedélyezett tengelyterhelésekre, (iii) a modell validálása a 2015-2018 közötti BWIM-mérések alapján. A járműforgalom sztochasztikus modellezése során a valószínűségi eloszlásokat empirikus módon határozták meg, a teherhatásokra pedig 45 különböző hatásábrán (nyíróerő, nyomaték) végeztek elemzéseket különböző fesztávokra (10-200 m) [22].
A szimuláció eredményei szerint az engedélyezett össztömeg-növekedések (akár 15%) és a nagyobb járműkombinációk elterjedése miatt a forgalmi igénybevételek érezhetően növekedtek, különösen a folytatólagos többtámaszú tartók és a hosszabb támaszközű hidak esetében. A finn α-tényezők újrakalibrálása megtörtént, értékeik nőttek, amely a nehezebb teherforgalmat tükrözi. A finn eljárás extrapolációt csak korlátozott mértékben alkalmazott, a jövőbeli forgalomnövekedést inkább folyamatos monitorozással kívánja követni.
Mérési adatok alapján meghatározott tehermodellek Európában városi környezetben – Aktuális kutatások esettanulmányai II.
Amszterdam – Hollandia városi tehermodell
Az Eurocode forgalmi tehermodelljei autópályaméréseken alapulnak, ezért városi hidak esetén gyakran túlbecslik a valós terheket, ezzel túltervezést eredményezve. A holland városi úthálózatra vonatkozó mérési adatok hiányában egy autópályás adatbázist szűrtek a városi forgalom jellemzőire, majd valószínűségi modelleken alapuló módszerrel módosították az EN 1991-2 LM1 és LM2 tehermodelleket. Az eredmények alapján a szóló és ikertengely terhek csökkentek, míg az első sáv megoszló terhelése rövid fesztávú hidaknál növekedtek. Az új modell jelentősen mérsékli a meglévő városi hidakra számított terheket, reálisabban tükrözve a tényleges forgalmat [24].
Amszterdam területén 850 híd van, amik között nem ritka a 100-200 éves szerkezet sem. A városvezetés meg akart bizonyosodni arról, hogy a kezelésében és tulajdonában lévő hídállományon a közlekedés fenntartható, illetve, ha ez nem lehetséges, akkor milyen intézkedéseket kell bevezetni a belváros biztonságos működtetése szempontjából. Amszterdamban WIM szenzorokkal mérték mértékadó pontokban az úthálózat terhelését – kifejezetten városi környezetre kalibrált mérési módszerrel [25] –, majd valószínűség-elméleti eljárással a mérést kiterjesztették a teljes belvárosra. Ez egy igen komplex vizsgálat volt, ami figyelembe vette a hídállomány életkorát, nyílástartományát, jellemző meghibásodásokat is. A kutatás eredményeképpen a koncentrált forgalmi teherszorzó értékét lecsökkentették αQ = 0,65 értékre, míg a megoszló teherszorzó értékét az országosan alkalmazott αq = 1,0 értéken választották meg [26], [27].
Rotterdam – Hollandia városi tehermodell
Hollandiában, Rotterdamban is elvégezték a rövid fesztávú városi hidakra vonatkozó forgalmi tehermodellek kalibrációját WIM-mérések alapján [28]. A mérési program célja a nagyvárosi forgalom sajátosságait figyelembe vevő valószínűségi tehermodell kidolgozása volt. A méréseket több, rövid fesztávú (15-25 m) hídon végezték, ahol a WIM-érzékelők segítségével járműtömeget, tengelyelrendezést és tengelyterheléseket rögzítettek, majd ezeket a forgalmi mintákat Monte Carlo-szimulációval hosszú távra extrapolálták.
A kiértékelés kimutatta, hogy a városi forgalomban a nehéz tehergépjárművek aránya alacsonyabb, viszont a járművek követési távolsága és sebessége is kisebb, ami a dinamikus hatások növekedését eredményezi. A mért terhelés hatására kapott igénybevételek (nyomaték és nyíróerő) eloszlását az LM1 modellből kapott értékekkel vetették össze. Az eredmények alapján az LM1 modell 5-10%-kal konzervatívabb a rotterdami mérésekhez képest, így egy helyspecifikus, probabilisztikus tehermodellt javasoltak rövid fesztávú városi hidakhoz. A kalibrált modell kisebb α-tényezőket eredményezett, mint az országos értékek.
Stuttgart – Németország városi tehermodell
A stuttgarti önkormányzat megbízásából 2015-ben a német Nemzeti Melléklettel kiegészített Eurocode 1-2 forgalmi terhelési modelljének alkalmazhatóságát vizsgálták kisfesztávú, városi hidak esetében [29]. (Megjegyzendő, hogy már korábban is készültek tanulmányok a városi környezetben elhelyezkedő hidak forgalmi terheinek csökkentésére, hiszen már korábban is megfigyelték, hogy a Nemzeti Melléklet nagymértékben túlbecsüli a terheket városi környezetben [30].) A kutatást a stuttgarti városvezetés annak érdekében kezdeményezte, hogy felmérjék a nagy forgalmú autópályahidakra kalibrált LM1 modell mekkora mértékű túlméretezéshez vezet a tipikusan 5-35 m közötti fesztávú, legfeljebb két sávos városi hidaknál. A szerzők a németországi országos forgalmi mérések járműtípusonkénti tengelyterhelési, eloszlási és gyakorisági adatait használták fel, amelyek alapján sztochasztikus forgalmi modellezést, hatásábra elemzést és 1000 éves visszatérési idejű karakterisztikus hatások számítását végezték. A torlódási helyzeteket külön sztochasztikus modellel, Turkstra-féle eljárással kezelték.
Eredményeik alapján az LM1 modell – különösen a német Nemzeti Melléklet α-tényezőit figyelembevéve – a vizsgált hidak esetében számottevően meghaladja a tényleges igénybevételi szinteket, ami indokolatlan biztonsági többletet és gazdaságtalan méretezést eredményez. A kalibráció azt mutatta, hogy a koncentrált járművet leíró αQi tényező egységes 0,7 értékre csökkentése mellett a szerkezetek továbbra is teljesítik az Eurocode által előírt megbízhatósági követelményeket [29]. A tanulmány így egy olyan, kifejezetten városi hidakra optimalizált módosított terhelési szint alkalmazását javasolja, amely helyi szinten csökkentheti az új hidak túlzott méretezéséből adódó költségeket, miközben a szerkezeti biztonság azonos mértékű marad.
Módszertan
A bemutatott külföldi példák alapján megállapítható, hogy Európa számos országában folyik kutatás-fejlesztés a hidakat érő hasznos teherszintek adat alapú meghatározására. Az is megállapítható, hogy egészen más megfontolásokat kell alkalmazni városi és országos (tranzit) hálózati elemeken. Jó egyezés mutatkozik a szabványos (alkalmazott) forgalmi terhelés meghatározására a különböző országokban, városokban. Az alábbiakban ezt a módszertant összegezzük és mutatjuk be az 5. ábrán:
- Az Eurocode bevezetésével a Nemzeti Mellékletek az alapértékeket rögzítették, így a méretezés a 2000-es években ezekkel az értékekkel történt. Ez a gyakorlatban azt jelentette, hogy a legtöbb ország az 1980-as években, Auxerre-ben (Franciaország) végzett mérésekből származó adatsor alapján határozta meg a forgalmi terhelést. Ezzel párhuzamosan azonban számos kutatási és adatgyűjtési program indult el, amelyek keretében megkezdődött a WIM-szenzoros adatgyűjtés.
- Mindenekelőtt a feladat körülhatárolása, a célkitűzés történik meg. A feladat tárgyi vagy térbeli? Mely úthálózatra, milyen hídtípusokra, milyen forgalmi feltételezések mellett történjen a vizsgálat?
- WIM szenzoros méréssel a közúthálózat (város vagy ország) reprezentatív pontjain adatfelvétel történik. A technológiai lehetőségek már meghaladták a 80-as éveket, így robosztusabb adatbázis hozható létre, mint az Eurocode kalibrációs Auxerre-i mérése.
- Az adatbázis ismeretében következő lépésként a mérési adatok szelektálása, csoportosítása történik meg a típusjárművek szerint. A legtöbb vizsgált és bemutatott szituációban a mérés kiegészül olyan járműterhelésekkel, amelyek adott esetben kimaradtak a mérési programból (pl. autódaru, katonai járművek), de gyakorlati megfontolások alapján előfordulhatnak. A tisztított és kiegészített adathalmazból végezhető el a statisztikai kiértékelés és az eloszlásfüggvény illesztése. A WIM adatokból sztochasztikus forgalmi modell készítendő a tengelyosztályok, sávváltások, követési távolságok valószínűségi modelljeinek definiálásával. Az 1000 éves visszatérési idő figyelembevételével meghatározható a teherintenzitás.
- A tehermodell megalkotásához statisztikai alapú feldolgozással történik az adott terület – országos vagy városi léptékű – közúti hídállományára vonatkozóan. A dominánsan kisnyílású hídszerkezeteket lefedő tehermodellnél a megoszló terhelés alapértéken tartása mellett célszerű a koncentrált teher módosítását előtérbe helyezni. Olyan területeken, ahol a nagynyílású hídszerkezetek dominálnak, a megoszló terhelés módosítása lehet célszerű. Az Eurocode tehermodelljei 200 m-es hídnyílásig alkalmazhatóak, e feletti hídnyílások esetén egyedi tehermodell megalkotása szükséges.
- A tehermodell kalibrációjához (αqi=1…n és αQi=1…n) különböző fesztávolságú hídmodelleken szimulációk végzendőek. Cél, hogy a mérési adatok alapján keltett igénybevételek minél jobb egyezést mutassanak a javasolt tehermodellel kapott igénybevétel-szintekkel.
- A forgalom sztochasztikus modellje és annak hatásai validálható in-situ mérésekkel, szükség esetén a teherszorzók finomíthatók. A szimulációkkal megfelelően kalibrált tehermodell alkalmas adott terület (ország, város vagy régió) méretezési hasznos terhének definiálásához.
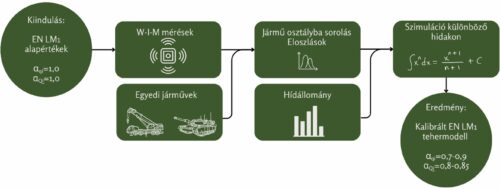 |
A módszertanban két olyan jelentős stratégiai döntést kell meghozni, amely nagyban befolyásolja a végeredményt. Egyrészről, hogy milyen additív járműveket teszünk hozzá a mérési adatokhoz, másrészről pedig, hogy a vizsgált hídállományt hogyan határoljuk le.
Összegzés
Jelen cikkben összefoglaltuk az Eurocode szerinti forgalmi tehermodellek kialakulását. A WIM technológia elterjedt alkalmazásával olyan adatgyűjtést lehet végezni, ami a valós forgalmi terhelésekről ad megbízható információt. Ezen adatok feldolgozásával lehetőség van az LM1 tehermodell αqi és αQi osztályba sorolási tényezőinek kalibrálására. Számos városban, régióban és teljes országokra is elvégezték ezt a kalibrációt. A tanulmányban bemutattuk, hogy milyen módszerrel dolgoztak a különböző projekteken.
Az Eurocode és az azzal összhangban kidolgozott Útügyi Műszaki Előírásban lehetőség lenne a cikkünkben ismertetett módszertan segítségével kalibrált közúti forgalmi tehermodell megalkotására. Mindemellett szükséges lenne az osztályba sorolás szempontrendszerét is megújítani, ugyanis az LM1 tehermodell és a valós közúti terhelés közötti összefüggés sokkal inkább függ a hídnyílás tartományától, mintsem az úthálózatban betöltött szerepétől.
Az Eurocode bevezetése előtt végzett mérések az akkori kor technológiai színvonalának megfelelően készültek. A jelenlegi, burkolatba épített súlymérési technológia lényegesen robosztusabb adatfelvételeket tesz lehetővé, így a tehermodell kalibráció is pontosabb lehet. Azokban az országokban, ahol az α-tényezőket mérési adatokon alapuló kalibrációval határozták meg és a Nemzeti Mellékletben rögzítették, a hidak méretezése az adott úthálózati kategóriába sorolás után lényegesen gazdaságosabban történhet. A forgalom alakulását és a közlekedési környezet változásait többféleképpen lehet követni. A finn megközelítés szerint a tehermodellek időszakos újrakalibrációja zajlik folyamatos WIM-mérések alapján, így nemcsak a fokozatos forgalomnövekedésből eredő terhelésváltozás követhető nyomon, hanem az olyan hirtelen, rendszerszintű változások is, mint például egy politikai döntéssel bevezetett, szigorúbb tengelyterhelési korlátozás, amely hirtelen átrendezi a járműflotta összetételét. A német megközelítés ezzel szemben a forgalmi trendek és járműkarakterisztikák extrapolációjára építette a jövőbeni terhelések becslését, amely bizonyos esetekben túlbecsléshez vezetett – ezt mutatja, hogy helyi kalibrációval (pl. Stuttgart) a ténylegesen fellépő terhelések jelentős mértékben csökkenthetők voltak.
Magyarországon jelenleg is kiterjedt mérőállomás-hálózat van, melyek adatai felhasználhatóak lennének a tehermodell pontos meghatározására. A MAÚT által létrehozott Hidak teljesítmény alapú méretezése 1. munkabizottságban ezt a projektet készítjük elő, hogy a fent ismertetett módszertan végigvitelével a magyarországi tehermodell is a valós forgalmi terhelésnek megfelelő lehessen.
Mindez nem csupán a tudományos megalapozottság miatt fontos, hanem a hídépítések gazdaságos megvalósítása és az anyagfelhasználás csökkentésére tett erőfeszítések érdekében is. A közeljövőben minél nagyobb hangsúlyt kell fektetnie az építésgazdaságnak a csökkentett CO2 kibocsátással megvalósítható szerkezetépítésre. Ennek legkönnyebb formája az anyagmennyiségek korlátozása, melynek feltétele a valós igényeknek megfelelő tehermodellek kidolgozása.
Célszerű ennek a munkának az eredményeit az Eurocode 2. generációs szabványkiadás során a Nemzeti Melléklet kidolgozása során a Magyar Szabványügyi Testületnek is figyelembe vennie.
Támogatás
Az Útügyi Műszaki Szabályozási Bizottság döntésére, 2025 áprilisában új MAÚT-munkabizottság (Magyar Út- és Vasútügyi Társaság) alakult a közúti hidak hasznos teherszintjének meghatározásához kapcsolódóan. A készítendő szakmai háttéranyag célja a tényleges közúti forgalmon alapuló statisztikai teherszintből számítható közúti híd hasznos terhek elemzése, vizsgálva a Magyar Közút NZrt. (MK) mérlegelési adatsorainak használhatóságát az Európában alkalmazott példák tükrében. A bizottsági elemzés tervezett befejezési határideje 2026. április. A munkabizottságot Hajós Bence vezeti, tagok: Sitku László, dr. Kovács Tamás, dr. Boros Vazul, Kővári Ákos és Németh Gábor.
Jelen tanulmány a Hidak teljesítmény alapú méretezése 1. című MAÚT-munkabizottság kutatásához kapcsolódóan készült.
Irodalomjegyzék
[1]: L. Sanpaolesi & P. Croce. 2005. Handbook 4 – Design of Bridges: Guide to Basis of Bridge Design Related to Eurocodes Supplemented by Practical Examples. In Leonardo da Vinci Pilot Project, no. CZ/02/B/F/PP-134007. Pisa, Italy, https://eurocodes.jrc.ec.europa.eu/sites/default/files/2021-12/handbook4.pdf
[2]: CEN, EN 1991-2: Eurocode 1: Actions on structures – Part 2: Traffic loads on bridges. Brussels, Belgium, 2003.
[3]: Farkas G., Kovács T., & Szalai K. 2010. Tartószerkezeti Eurocode-ok – Javaslat a hazai alkalmazás legfontosabb nemzeti paramétereire – 1. rész. Beton, 18(5) pp. 3–7.
[4]: MAÚT, e-ÚT 07.01.12: Erőtani számítás. Közúti hidak tervezése (KHT) 2. Budapest, Hungary, 2011.
[5]: Farkas G., Kovács T., & Szalai K. 2010. Tartószerkezeti Eurocode-ok – Javaslat a hazai alkalmazás legfontosabb nemzeti paramétereire – 2. rész. Beton, 18(6) pp. 10–14.
[6]: R. Bartus, Á. Kővári, és G. Németh. 2023. Észrevételek és javaslatok a készülő új eUT 07.01.12 közúti hidak erőtani számítása Útügyi Műszaki Előíráshoz. Útügyi Lapok, 11(18) pp. 1–19. https://doi.org/10.36246/UL.2023.2.01
[7]: U. Freundt, Szerk. 2011. Anpassung von DIN-Fachberichten „Brücken” an Eurocodes. In Berichte der Bundesanstalt für Strassenwesen B, Brücken- und Ingenieurbau, no. 77. Bremerhaven, Wirtschaftsverlag NW, Verlag für neue Wissenschaft.
[8]: D. Papastergiou & mtsai. 2025. Überprüfung bestehender Strassenbrücken mit einem aktualisierten Verkehrslastmodell. Bundesamt für Strassen ASTRA, Bern, Switzerland, ASTRA 82001, https://www.astra.admin.ch/dam/astra/de/dokumente/standards_fuer_nationalstrassen/astra_82001_ueberpruefungbestehenderstrassenbruecken2006.pdf.download.pdf/astra_82001d.pdf
[9]: TRL Limited, A guide to axle load surveys and traffic counts for determining traffic loading on pavements. Transport Research Laboratory, Crowthorne, United Kingdom, 40.
[10]: H. van Loo & A. Znidaric. 2021. Guide for Users of Weigh-In-Motion, 3rd Edition. International Society for Weigh-In-Motion (ISWIM.
[11]: R. J. Woodward. 2001. Bridge Management in Europe – Deliverable D14 Final Report, D14, március 2001.
[12]: Hajós B. 2025. WIM-méréstechnika rövid története, különös tekintettel a magyarországi alkalmazási lehetőségekre. Útügyi Lapok, 13(22) 12-24., 2025. https://doi.org/10.36246/UL.2025.2.02
[13]: M. Nowak & O. Fischer. 2025. Refined Vehicle Classification for BWIM Traffic Data and the Effects on Traffic Load Modelling. IABSE Congress, Ghent 2025, The Essence of Structural Engineering for Society, Ghent, Belgium, pp. 2219–2227. https://doi.org/10.2749/ghent.2025.2219
[14]: M. Soudijn, S. Van Rossum, & A. De Boer. 2021. Measuring heavy traffic with WIM-ROAD and WIM-BRIDGE systems in an urban environment. IABSE Congress, Ghent 2021, Structural Engineering for Future Societal Needs, Ghent, Belgium, pp. 331–340. https://doi.org/10.2749/ghent.2021.0331
[15]: M. Sjaarda, T. Meystre, A. Nussbaumer, és M. A. Hirt, „A systematic approach to estimating traffic load effects on bridges using weigh‐in‐motion data”, Stahlbau, köt. 89, sz. 7, o. 585–598, júl. 2020, https://doi.org/10.1002/stab.202000048
[16]: D. Skokandić, A. Žnidarič, A. Mandić Ivanković, & M. Kreslin. 2017. Application of Bridge Weigh-in-Motion measurements in assessment of existing road bridges. In Proceedings of the Joint COST TU1402 – COST TU1406 – IABSE WC1 Workshop, The Value of Structural Health Monitoring for the reliable Bridge Management, University of Zagreb Faculty of Civil Engineering, máj. 2017, pp. 4.6-1-4.6-8. https://doi.org/10.5592/CO/BSHM2017.4.6
[17]: A. S. Nowak & P. Rakoczy. 2013. WIM-based live load for bridges. KSCE Journal of Civil Engineering, 17(3) pp. 568–574, ápr. 2013, https://doi.org/10.1007/s12205-013-0602-8
[18]: S. Martinolli & mtsai. 2025. Quantification of hidden safety reserves between different highway traffic load models based on probabilistic calibration analysis. IABSE Congress, Ghent 2025, The Essence of Structural Engineering for Society, Ghent, Belgium, pp. 58–66. https://doi.org/10.2749/ghent.2025.0058
[19]: A. Natali, A. Cosentino, F. Morelli, & W. Salvatore. 2023. Multilevel Approach for Management of Existing Bridges: Critical Analysis and Application of the Italian Guidelines with the New Operating Instructions. Infrastructures, 8(4) pp. 70, március 2023, https://doi.org/10.3390/infrastructures8040070
[20]: S. Celati, A. Natali, & W. Salvatore. 2025. Traffic models for Italian provincial roads. IABSE Congress, Ghent 2025, The Essence of Structural Engineering for Society, Ghent, Belgium, pp. 366–374. https://doi.org/10.2749/ghent.2025.0366
[21]: M. Nowak, O. Fischer, T. Tepho, & U. Willberg. 2023. Verkehrsmonitoring an einer Autobahnbrücke – Datenerfassung zur lokalen Verkehrscharakteristik als Grundlage für objektspezifische Verkehrslastmodelle. Beton und Stahlbetonbau, 118(9) pp. 636–648, szept. 2023, https://doi.org/10.1002/best.202300043
[22]: O. Asp & A. Laaksonen. 2023. Traffic Load Model Calibration and Comparison to Evolving Traffic Loads In 2014–2018. BJRBE, 18(3) pp. 139–168. https://doi.org/10.7250/bjrbe.2023-18.612
[23]: Finnish Transport Agency. 2018. Bridge WIM Overview Report – Year 2013–2017. Finnish Transport Agency, Engineering and Environment, Helsinki, Finland, Research report 29/2018.
[24]: L. C. La Gasse, R. D. J. M. Steenbergen, & D. L. Allaix. 2019. Traffic load model for road bridges in the urban road network. Heron, 64(3) pp. 297–318.
[25]: M. L. Soudijn, S. Van Rossum, & A. De Boer. 2023. Measuring heavy traffic using alternative systems in an urban environment. In Life-Cycle of Structures and Infrastructure Systems, 1. kiad., London, CRC Press, pp. 2873–2880. https://doi.org/10.1201/9781003323020-349
[26]: A. Vervuurt, B. Cerar, L. La Gasse, R. Steenbergen, & A. De Boer. 2025. Traffic load model for the inner city of Amsterdam. IABSE Congress, Ghent 2025, The Essence of Structural Engineering for Society, Ghent, Belgium, pp. 2159–2166. https://doi.org/10.2749/ghent.2025.2159
[27]: M. Soudijn, S. Van Rossum, F. Van Waarde, & A. De Boer. 2025. A reduced traffic load model for the inner city of Amsterdam. IABSE Congress, Ghent 2025, The Essence of Structural Engineering for Society, Ghent, Belgium, pp. 2247–2255. https://doi.org/10.2749/ghent.2025.2247
[28]: L. Hellebrandt, C. B. M. Blom, & R. D. J. M. Steenbergen. 2014. Probabilistic traffic load model for short-span city bridges. Heron, 59(2/3) pp. 33–56.
[29]: V. Boros, B. Novák, & U. Decker. 2015. Modifiziertes Verkehrslastmodell für kommunale Brückenbauwerke. Beton und Stahlbetonbau, 110(9) pp. 620–627. szept. 2015, https://doi.org/10.1002/best.201500024
[30]: B. Novák, S. Brosge, K. Barthel, & W. Pfisterer. 2007. Anpassung des Verkehrslastmodells des DIN FB 101 für kommunale Brücken. Beton und Stahlbetonbau, 102(5) pp. 271–279. máj. 2007, https://doi.org/10.1002/best.200700546
Erre a szövegre így hivatkozhat:
Kővári Ákos, Németh Gábor: Az EUROCODE szerinti forgalmi tehermodellek kialakulása, alkalmazása és kalibrációja WIM adatokkal, 2025, DOI: 10.36246/UL.2025.2.03
