https://doi.org/10.36246/UL.2025.2.05
2025; 13. évfolyam, 22. szám
Bevezető
Ebben a cikkben egy egyszerű példán szemléltetjük, hogy a Magyarországon mért valós járműterhek alapján számolt karakterisztikus igénybevételek miként viszonyulnak az Eurocode által javasolt tehermodellhez. Ehhez lényegében ugyanazt az eljárást követjük, amelyet már Németországban is alkalmaztak a városi forgalom összehasonlítására a különböző tehermodellekben megfogalmazott értékekkel [1, 2]. Először röviden ismertetjük mely méréseket vesszük alapul és miként közelítjük azokat. Leírjuk miként számítjuk a tehergépforgalomból adódó karakterisztikus igénybevételeket egy egysávos, kéttámaszú tartó esetén, majd összehasonlítjuk az eredményeket az Eurocode által javasolt, illetve a Magyarországon jelenleg hatályos és a most javasolt értékekkel.
Magyarországon mért járműterhek
A cél az volt, hogy – a Németországban is alkalmazott eljáráshoz hasonlóan – a valós forgalmat néhány jellemző járműtípus felhasználásával modellezzük [3, 4]. Ehhez először is kiválasztottunk egy mérvadónak tekinthető mérőállomást, miután kielemeztük négy magyarországi mérőállomás (Ártánd, Lajta, Kengyeles és Kéthalom) mindkét irányának mérési adatait a 2024-es évből. Ezzel kapcsolatos további részleteket az [5] tartalmaz. A választás az ártándi határállomás kilepő forgalmára esett. Egyrészt itt minden tehergépkocsi súlya feljegyzésre kerül, ellentétben azokkal a mérőállomásokkal, ahol csak a járművek egy részét tereli ki a mérési rendszer a megállításos, egyedi mérlegelésre, amelyeket az előszűrés kiválogat. Így nem csak jóval több adat áll rendelkezésre, mint más mérőállomások esetén, de az adatok sokkal inkább reprezentatívnak tekinthetőek. Azért választottuk a kifelé irányuló forgalmat, mert itt valamivel kedvezőtlenebbnek mutatkozott a nehéz járművek részesedése.
A következő lépésben kiválasztottuk azt az öt járműtípust (1. ábra), amelyek a leggyakrabban előfordultak a mérési eredmények között.
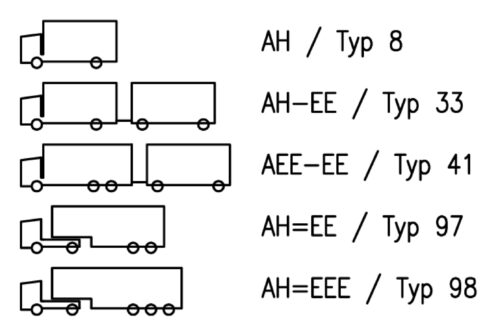 |
Ezek tökéletesen megegyeztek a Németországban is használt öt járműtípussal, [1] és ezek összesen, több mint a járművek 95%-át tették ki. A fennmaradó járműveket, amelyeknek kisebb a részaránya, arányosan felosztottuk a kiválasztott öt járműtípusra, majd a korrigált arányokat kerekítettük. Mindezeket az 1. táblázat foglalja össze. (A magyar tengelyképlet jelölésben minden betű egy-egy tengelyt jelent, a kötőjel pótkocsit jelöl, az egyenlőség jel pedig a nyerges szerelvény félpótkocsiját.)
| Tengelyképlet | AH | AH-EE | AEE-EE | AH=EE | AH=DDD | egyéb |
| Német típusnév | Typ 8 | Typ 3 | Typ 41 | Typ 97 | Typ 98 | |
| Darabszám | 8 838 | 1 429 | 3 524 | 36 614 | 239 940 | 13 395 |
| Mért arány | 2,91% | 0,47% | 1,16% | 12,05% | 79,00% | 4,41% |
| Korrigált arány | 3,04% | 0,49% | 1,21% | 12,61% | 82,64% | |
| Kerekített arány | 3,00% | 0,50% | 1,50% | 12,50% | 82,50% |
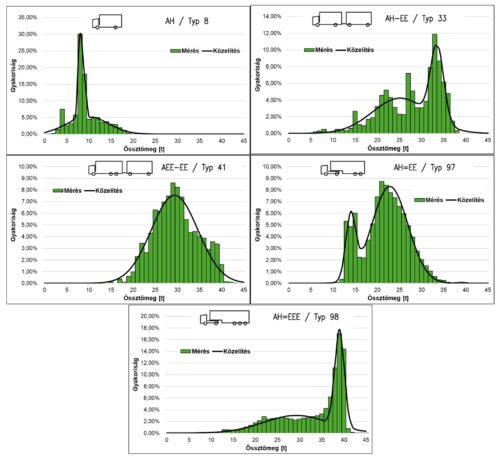
Ami a tehergépkocsik éves darabszámát illeti, itt az ártándi belépő forgalmat vettük alapul, mivel ez a 314 598 jármű pár százalékkal több mint a kilépő forgalom (303 740 jármű). A következő lépésben a kiválasztott öt jármű tehereloszlását két normál eloszlás lineáris kombinációjával közelítettük, a német számítások mintájára. Ehhez az eloszlások paramétereit (középérték, szórás és a két eloszlás aránya) a legkisebb négyzetek módszerét alkalmazva optimalizáltuk. Az így kapott paramétereket, már kN-ra váltva a 2. táblázat tartalmazza. Ennél talán szemléletesebben mutatja a közelítések pontosságát az 2. ábra, melyben a mért és számított gyakoriságfüggvényeket ábrázoltuk, a koherencia megőrzése érdekében itt viszont tonnában kifejezve.
| Járműtípus | μ1 [kN] | σ1 [kN] | ξ1 | μ2 [kN] | σ2 [kN] | ξ2 |
| AH / Typ 8 | 78,1 | 4,3 | 0,390 | 92,3 | 45,7 | 0,610 |
| AH-EE / Typ 33 | 246,8 | 62,9 | 0,666 | 329,9 | 14,5 | 0,334 |
| AEE-EE / Typ 41 | 54,9 | 5,6 | 0,000 | 288,8 | 52,7 | 1,000 |
| AH=EE / Typ 97 | 134,7 | 10,7 | 0,149 | 223,2 | 40,8 | 0,851 |
| AH=DDD / Typ 98 | 287,7 | 74,0 | 0,561 | 385,4 | 10,2 | 0,439 |
 |
Karakterisztikus igénybevételek kiszámítása
A valós forgalomból adódó karakterisztikus igénybevételek kiszámításához a tehereloszlásokon felül szükség van még a járművek geometriájának, illetve az össztömeg tengelyekre való felosztásának az ismeretére. Tekintve, hogy korábbi vizsgálatok alapján a Németországban és a Magyarországon megfigyelt járművek ezen paraméterei jó egyezést mutattak [5, 7], a Németországban is alkalmazott, 3. és 4. táblázat szerinti értékeket vettük alapul.
| Járműtípus | Tengelytáv 1 → 2 |
Tengelytáv 2 → 3 |
Tengelytáv 3 → 4 |
Tengelytáv 4 → 5 |
| AH / Typ 8 | 4,46 | – | – | – |
| AH-EE / Typ 33 | 4,93 | 6,47 | 5,00 | – |
| AEE-EE / Typ 41 | 4,65 | 1,34 | 5,17 | 4,64 |
| AH=EE / Typ 97 | 3,72 | 6,59 | 1,32 | – |
| AH=DDD / Typ 98 | 3,73 | 5,61 | 1,30 | 1,30 |
| Járműtípus | 1. tengely | 2. tengely | 3. tengely | 4. tengely | 5. tengely |
| AH / Typ 8 | 44,9 | 55,1 | – | – | – |
| AH-EE / Typ 33 | 25,8 | 37,2 | 18,9 | 18,1 | – |
| AEE-EE / Typ 41 | 20,9 | 25,8 | 16,1 | 19,5 | 17,7 |
| AH=EE / Typ 97 | 30,6 | 30,9 | 19,1 | 19,4 | – |
| AH=DDD / Typ 98 | 20,8 | 28,1 | 17,0 | 17,0 | 17,1 |
A számításnál egy három méter széles forgalmi sávot vettünk alapul. Az útfelületi egyenetlenségekből eredő kölcsönhatások a jármű és a tartószerkezet között dinamikus hatásokat válthatnak ki. Ezek figyelembevétele érdekében a [8] alapján a forgalomban haladó tehergépjárművek esetében a DIN 1072 [9] szerinti dinamikus együtthatót alkalmaztuk.
Ugyanakkor elvégeztünk egy olyan számítást is, amelynél feltételeztük, hogy a hídon átkelő járművek 10%-a torlódásban halad át a hídon. Mivel az AH=DDD tengelyképletű nyergesvontatók adják az összforgalom túlnyomó részét, egyszerűsítésként azt feltételeztük, hogy torlódás esetén az egész sávot ilyen típusú teherautók foglalják el. A járművek között az első és hátsó tengelytől számított 1,0 m-es túlnyúláson felül további 1,0 m-es távolságot feltételeztünk. Továbbá egyszerűsítésképpen abból indultunk ki, hogy az összes, egyszerre torlódásban álló jármű össztömege azonos, vagyis a terhelésük tökéletesen korrelál. Ezek a feltételezések kissé kedvezőtlenek és nagy támaszközök esetén konzervatív eredményeket adnak, de a vizsgált támaszköz-tartományban elfogadhatóak.
Az első lépésként meghatároztuk a maximális nyíróerő és a maximális mezőnyomaték értékét minden vizsgált támaszközre és járműtípusra vonatkozóan. Ehhez a különböző járműtípusokhoz tartozó tengelyek távolságával és terhelési arányával meghatározott erő-csoportot egységes össztömeggel lépésről lépésre léptettünk keresztül a vizsgált hídon és megkaptuk a mértékadó pozícióból adódó maximális pozitív nyomaték, illetve nyíróerő értékét. Így meghatároztunk egy az adott járműtípus teljes tömegéhez viszonyított \( \eta_i \) hatástényezőt, amely megadja a maximális nyomaték, illetve nyíróerő értékét a jármű össztömegének függvényében.
Mivel az egyes járműtípusok össztömegét bimodális normális eloszlással közelítettük, a maximális igénybevételek eloszlásfüggvényét úgy kaptuk meg, hogy ezeket az eloszlásokat megszorozzuk a megfelelő járműarányokkal és hatástényezőkkel, majd összeadjuk. Tehát az egyes járművek áthaladásából adódó maximális igénybevétel eloszlásfüggvénye normális eloszlások lineáris kombinációjaként előállítható. Mivel a különböző járművek össztömege független valószínűségi változónak tekinthető, évente 315 000 tehergépkocsit feltételezve az 1000 évente fellépő karakterisztikus teher átlagos visszatérési periódusa \( m_{T_R}=315\ 000\bullet1000 \). Így az karakterisztikus igénybevételre a következő összefüggésnek kell teljesülnie [10]:
\[ F\left(r\right)=\sum_{i}{\Phi\left(\frac{r-\mu_i}{\sigma_i}\right)\bullet\xi_i\bullet\eta_i}=1-\frac{1}{m_{T_R}} \]
Ebből az egyenletből numerikusan meghatározható az egyetlen ismeretlen, a keresett igénybevétel r karakterisztikus értéke.
Számítási Eredmények
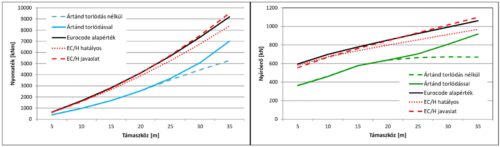
A felvázolt számítást elvégeztük egy egysávos, 3 m széles, kéttámaszú tartó esetén hétféle támaszközre 5 és 35 m között. Megkülönböztettünk egy olyan esetet, amelyik nem vesz figyelembe torlódásokat és egy olyat is, amelyik 10% torlódással számol. A számításokat mind a maximális nyomaték, mind pedig a maximális nyíróerő karakterisztikus értékének meghatározására elvégeztük. Az így kapott értékeket az Eurocode-ban meghatározott LM1 tehermodellel vetettük össze. Itt három változatot különböztettünk meg. Egyrészt az Eurocode által javasolt alapértékeket, ahol minden terhelési osztályba sorolási tényező értéke 1,0. Továbbá a jelenleg Magyarországon hatályos értékeket az I. terhelési osztály esetén (αQ1=1,0; αq1=0,8). Végezetül pedig a [11] által javasolt értékeket, szintén az I. terhelési osztályra vonatkozóan (αQ1=0,9; αq1=1,0). Az eredményeket a 3. ábra szemlélteti a maximális nyomatéki, illetve nyírási igénybevételek esetén.
 |
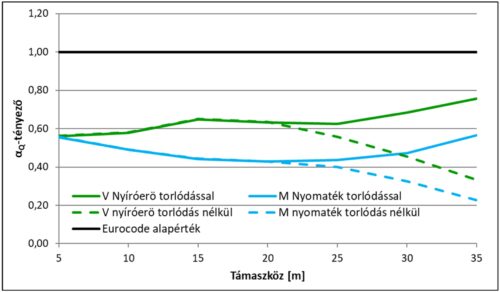
Ezen felül érdemes azt is megvizsgálni, hogy az egyes α-tényezők milyen értéke mellett felelne meg az Eurocode által definiált teherből adódó igénybevétel a valós forgalmi adatokon alapuló karakterisztikus értéknek. A vizsgált rövid támaszközök esetén itt érdemes a koncentrált teher α-tényezőjét alapul venni, mivel ennek van a jelentősebb hatása. A megoszló teher α-tényezője a számítás során változatlanul 1,0 volt. Az így számított szükséges α-tényezőket a támaszköz függvényében a 4. ábra tartalmazza.
 |
Észrevételek és Megjegyzések
Az egyszerűsített példa eredményei arra utalnak, hogy a vizsgált esetekben mindhárom tehermodell konzervatív a valós forgalomhoz viszonyítva, azaz jóval nagyobb igénybevételeket eredményez, mint a közelítés alapján számított 1000 évente fellépő karakterisztikus érték.
A vizsgálat kizárólag a 35 m támaszközt nem meghaladó, egysávos, kéttámaszú hidakra korlátozódott. Mivel Magyarországon a 30 m legnagyobb támaszközt meghaladó hidak részaránya mindössze a teljes állomány hozzávetőleg 3%-át teszi ki [12], a vizsgált támaszköz-tartomány a magyar hidak túlnyomó részét magába foglalja. Természetesen ezek között keretszerkezetek és folytatólagos többtámaszú tartók is szerepelnek, melyeknél a nyomatéki igénybevételek értéke jelentősen eltér. Ugyanakkor, mint az eredményeken is látszik, a rövid támaszközök esetén jellemzően a nyíróerők a mértékadóak és itt a statikailag határozatlan szerkezetek kisebb eltérést mutatnak a vizsgált esetektől. Bizonyára az is egy jelentős egyszerűsítés, hogy csupán egy forgalmi sávot vettünk figyelembe, azonban lényegében minden közúti híd több sávos. Ebben az esetben, a vizsgáltnál jóval összetettebb teheresetek is felléphetnek, amennyiben tehergépkocsik egymást előzik. Ugyanakkor ezzel párhuzamosan a tehermodellből adódó igénybevételek is megnőnek. Jelen tanulmányban nem vettük figyelembe a forgalom esetleges növekedését, illetve azon járműveket, melyek megengedett össztömege túllépi a 40 tonnát, így útvonalengedély-kötelesek. Az alkalmazott közelítés azonban figyelembe veszi mindazokat a járműveket, melyek a kiválasztott leggyakoribb öt járműtípusba tartoznak és túllépik a megengedett 40 t össztömeget. Megjegyzendő, hogy elsősorban a legmeghatározóbb nyergesvontató esetében, a közelítés kifejezetten konzervatívnak tekinthető, amint az a 2. ábrából is kitűnik. A grafikon jobb oldalán, a legnagyobb tehertartományban a közelítő görbe jóval nagyobb arányú tehergépkocsit feltételez, mint ami a valóságban megfigyelhető. Számszerűsítve mindössze 3 olyan tehergépkocsi volt a 2024-es évben, mely túllépte a 45 tonnát míg a közelítő görbe alapján szinte 2500 ilyen jármű kellett volna legyen.
Jelen tanulmányban tudatosan ugyanazokat a módszereket alkalmaztuk, mint az Eurocode Németországban érvényes nemzeti mellékletének kalibrálása esetén tették. A közelítő függvény példája azonban jól szemlélteti, hogy hazánkban részben eltérőek a peremfeltételek, mint Németországban. Vélhetően a szigorúbb szabálykövetés az össztömeg terén arra vezethető vissza, hogy az ellenőrzések miatt jelentősen kevesebb túlsúlyos jármű közlekedik Magyarországon, mint Németországban. Így felmerül az a kérdés is, hogy a normál eloszlás alkalmas-e itt is a tehereloszlás valósághű modellezésére? Valószínűsíthető, hogy felső határral bíró eloszlástípusokkal, mint például a lognormális eloszlás, jóval jobb közelítés várható. Ezt mindenképpen érdemes alaposabban megvizsgálni, és a kutatást ez irányban folytatni, amennyiben egy olyan tehermodell megalkotása a cél, amely a magyarországi tehergépkocsi forgalmat reprezentatívan kívánja leképezni.
Összegzés
Az egysávos, kéttámaszú tartók példáján szemléltettük, hogy a Magyarországon mért valós járműterhek közelítése alapján számított karakterisztikus igénybevételek miként viszonyulnak az Eurocode által javasolt tehermodellhez. Mind az Eurocode alapértékei, mind a Magyarországon jelenleg hatályos tehermodell konzervatívnak bizonyult a vizsgált esetekben.
Rámutattunk arra is, hogy hazánkban a járművek terhelésének sűrűségfüggvénye kevésbé illeszkedik a normális eloszláshoz, mint Németországban. Ellenben felső határral bíró eloszlástípusokkal, mint például a lognormális eloszlás, jobb közelítés várható.
Fontos megjegyezni, hogy jelen számítás számos egyszerűsítést és közelítést tartalmaz, és a valós hidaknak csak egy kiválasztott szegmensét foglalja magába. Egy valósághű tehermodell megalkotásához további, átfogó számítások elvégzésére van szükség. A vizsgálat célja elsősorban az volt, hogy rámutasson miként használhatóak fel a rendelkezésre álló mérési adatok egy valósághű tehermodell megalkotásához, illetve adjon egy első indikációt, hogy a jelenlegi tehermodell lefedi-e a valós forgalmi terhet.
Támogatás
Az Útügyi Műszaki Szabályozási Bizottság döntésére, 2025 áprilisában új MAÚT-munkabizottság (Magyar Út- és Vasútügyi Társaság) alakult a közúti hidak forgalmi teherszintjének meghatározásához kapcsolódóan. A készítendő szakmai háttéranyag célja a tényleges közúti forgalmon alapuló teherszintből statisztikai alapon számítható közúti híd forgalmi terhek elemzése, vizsgálva a Magyar Közút NZrt. (MK) mérlegelési adatsorainak használhatóságát az Európában alkalmazott példák tükrében. A bizottsági elemzés tervezett befejezési határideje 2026. április. A munkabizottságot Hajós Bence vezeti, tagok: Sitku László, Dr. Kovács Tamás, Dr. Boros Vazul, Kővári Ákos és Németh Gábor.
Jelen tanulmány a Hidak teljesítmény alapú méretezése 1. című MAÚT-munkabizottság kutatásához kapcsolódóan készült.
Irodalomjegyzék
[1]: V. Boros, B. Novák, & U. Decker. 2015. Modifiziertes Verkehrslastmodell für kommunale Brückenbauwerke. Beton und Stahlbetonbau, 110(9) pp. 620–627. https://doi.org/10.1002/best.201500024
[2]: Kővári Ákos & Németh Gábor. 2025. Az EUROCODE szerinti forgalmi tehermodellek kialakulása, alkalmazása és kalibrációja WIM adatokkal. In Útügyi lapok 13(22) pp. 25-42. https://doi.org/10.36246/UL.2025.2.03
[3]: R. Kaschner, szerk. 2009. Auswirkungen des Schwerlastverkehrs auf die Brücken der Bundesfernstraßen. In Berichte der Bundesanstalt für Strassenwesen B, Brücken- und Ingenieurbau, no. 68. Bremerhaven: Wirtschaftsverlag NW, Verlag für neue Wissenschaft.
[4]: U. Freundt, szerk. 2011. Anpassung von DIN-Fachberichten „Brücken” an Eurocodes. In Berichte der Bundesanstalt für Strassenwesen B, Brücken- und Ingenieurbau, no. 77. Bremerhaven: Wirtschaftsverlag NW, Verlag für neue Wissenschaft.
[5]: Hajós Bence & Hajós Eszter Sára. 2025. A közúti teherforgalomban közlekedő járművek tényleges össztömeg mérési eredményei Magyarországon. Útügyi lapok 13(22) pp. 43-59. https://doi.org/10.36246/UL.2025.2.04
[6]: Boros Vazul. 2024. Közúti terhek statisztikai alapú meghatározása Németországban az Eurocode szerint – hazai alkalmazás lehetőségei. In Hajós Bence szerk. Hidász napok 2024 előadásainak gyűjteménye, Lánchíd füzetek 40. Biri, 154-170. https://hidak.hu/konyvek/Lanchid_40_HN2024.pdf
[7]: Boros Vazul, Kővári Ákos & Hajós Bence. 2025. Potentials of utilizing vehicle weight data for the calibration of national traffic load models for bridges. In Leonetti, D.; Snijder, H.H.; De Pauw, B.; Alphen, S. szerk. IABSE Congress Ghent 2025, The Essence of Structural Engineering for Society, Congress Proceedings, Zürich, International Association for Bridge and Structural Engineering IABSE pp. 2193-2200.
[8]: U. Freundt, S. Böning, & R. Kaschner. 2011. Straßenbrücken zwischen aktuellem und zukünftigem Verkehr – Straßenverkehrslasten nach DIN EN 1991-2/NA, Beton und Stahlbetonbau, 106(11) pp. 736–746, https://doi.org/10.1002/best.201100050
[9]: DIN 1072 Straßen- und Wegbrücken Lastannahmen. Dezember 1985.
[10]: G. Spaethe. 1992. Die Sicherheit Tragender Baukonstruktionen. Springer-Verlag, Berlin.
[11]: Horváth Adrián. 2024. Új e-ÚT 07.01.12:2024T előírásról – Újdonságok az e-ÚT 07.01.12:2011-hez képest. In Hajós Bence szerk. Hidász napok 2024 előadásainak gyűjteménye, Lánchíd füzetek 40. Biri, pp. 83-109. Online: https://hidak.hu/konyvek/Lanchid_40_HN2024.pdf
[12]: Hajós Bence. 2010. Összefoglaló a magyar közúti hídgazdálkodásról 2004-2010. In Hajós Bence szerk. Lánchíd füzetek 16. Biri, 1-28. https://hidak.hu/konyvek/Lanchid_16_hidgazdalkodas.pdf
Erre a szövegre így hivatkozhat:
Boros Vazul: A Magyarországon mért járműterhek alapján számolt karakterisztikus híd igénybevételek összehasonlítása az Eurocode tehermodelljével kéttámaszú tartók esetén, 2025, DOI: 10.36246/UL.2025.2.05
