Útpályaszerkezetek modellezése 1. rész
Ez a bejegyzés azzal a céllal jött létre, hogy a kedves érdeklődő olvasónak egy tömör összefoglalót nyújtson az útpályaszerkezetek modellezési lehetőségeiről. Terveink szerint az egyes számítási módszerekről később részletes összefoglaló írásokat is közreteszünk, amelyek segítségével már a gyakorló mérnökök is elvégezhetik méretezési számításaikat.
Rövid bevezetés az útpályaszerkezetek modellezésébe
Kezdetben a pályaszerkezeteket szinte a forgalom nagyságától és a talaj teherbírásától függetlenül, közel azonos anyagból és azonos vastagságban építették meg. Később a forgalom rohamos növekedésének hatására szükségessé vált, hogy az utak pályaszerkezetének vastagsága mind a forgalom nagyságával, mind a földmű minőségével arányos legyen. Ebben az időszakban dolgozták ki a gyakorlati megfigyeléseken, nagyminta kísérleteken és elméleti elgondolásokon alapuló empirikus és szemiempirikus méretezési módszereket. A kísérletek alatt valósághű körülmények között modellezték a pályaszerkezetek tönkremenetelét, melynek eredményeit statisztikai módszerek segítségével értékelték ki. Az empirikus eljárások a tényleges leromlási folyamat megfigyelésén alapulnak.
Az empirikus pályaszerkezet méretezési eljárások igen nagyot fejlődtek az 1950-es és 1960-as évek fordulóján. Ebben az időszakban ugyanis egyre égetőbb kérdéssé vált az, hogy miként lehet a nehéz tehergépkocsik útrongáló hatásait pénzegységben kifejezni. Ennek tisztázására 1958-ban és 1959-ben nagyszabású útkísérlet sorozatok indultak meg az USA Állami Útépítő Hivatalok Szövetsége szervezésében melyek később „AASHO-útkísérletek” néven váltak híresé. Az AASHO-útkísérletek empirikus úton nyert adathalmazán a következő három fő mennyiség között kerestek elvi összefüggést:
- a kísérleti szakaszok változó pályaszerkezetének vastagsága,
- a kísérletben részt vett terhelő járművek egyes tengelyeinek súlya,
- egy-egy tengelysúly jellemző ismétlődési száma.
A mérési eredményeket több kutatócsoport értékelte ki. A hajlékony pályaszerkezetek méretezési eljárását Finn-Shock dolgozta ki a mért adatokból. Meghatározták a szerkezeti rétegek egyenérték vastagságát, valamint a feldolgozás alapján bevezették az egységtengely fogalmát is. Az AASHO kísérletek eredményeit számtalan ország átvette és sikeresen alkalmazta. Magyarországon az 1971-ben megjelenő Hajlékony Útpályaszerkezetek Méretezési Utasítása (HUMU) című munkában jelentek meg eredményei.
 |
Az empirikus módszerek hátránya, hogy a kísérlet alatt felállított modellek csak a kísérlet körülményei között érvényesek. Sok estben viszont akkor is ezt a modellt használják, amikor már a körülmények nem felelnek meg a követelményeknek.
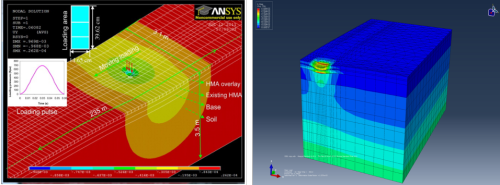
Az igények és az igénybevételek növekedése miatt csakhamar előtérbe kerültek a mechanikai alapokon nyugvó eljárások is. Ezt támasztja alá az Európai Unió által finanszírozott AMADEUS kutatás 1998-1999-ben folyt zárójelentése, mely kimutatta, hogy bár Európában – és világszerte másutt is – többféle megközelítéssel élnek az útburkolatok méretezésére, alapvető közös jellemzőjük mégis az, hogy a pályaszerkezetben a tengelysúlyok áthaladásának hatására keletkező erők, feszültségek és alakváltozások számításán alapulnak. Ezek a mechanikai alapú méretezési módszerek a pályaszerkezetet rugalmasságtani alapon számítható szerkezetként fogják fel. Az empirikus eljárásokkal szemben tehát az analitikus módszerek a szerkezet szilárdságtani modelljének a terhelésre adott fizikai válaszán alapulnak!
 |
 |
A rugalmas szilárd anyagra vonatkozó állapotegyenleteknek a megoldását Boussinesq rakta le még 1876-ban. A későbbi kutatások közben kiderült, hogy az olyan réteges szerkezetekre vonatkozóan, mint a hajlékony útpályaszerkezetek, a Boussinesq-féle állapotegyenleteknek nincsen zárt megoldásuk. A réteges szerkezetek méretezésére kidolgozott és alkalmazott mechanikai eljárások:
- az egyenérték vastagságon (Odemark),
- a rétegenkénti analitikus számításokon,
- a véges elemek módszerén (VEM).
- és a diszkrét elemek módszerén (DEM) alapulnak.
Az egyenérték-vastagság elvén alapuló módszerek estében a réteges szerkezeteket egy végtelen féltérré alakítják át, melyre már érvényesek és alkalmazhatók lesznek a Boussinesq-féle állapotegyenletek.
A rétegenkénti analitikus modellek általában Burmister elgondolásain alapulnak, melynek segítségével a pályaszerkezet bármely pontjában számíthatóvá válnak „közelítően” az ébredő erők, feszültségek és alakváltozások.
A végeselemes módszert alkalmazó eljárások a ma használatos modellek közül a legösszetettebbek és a legtöbb bemenő adatot igénylők. A végeselemes módszer egy numerikus módszer parciális differenciálegyenletek közelítő megoldására. Ekkor feltételezik, hogy a keresett függvény leírása a tér kisebb, már matematikailag jól kezelhető részekre bontásával az elemi függvényekből összeállítható. Az elemi függvények értelmezési tartományai nem fednek át és összegük az globális függvény értelmezési tartományát adja. A modellezéshez leginkább használatos végeselem a három kontrolpont alkotta térbeli háromszög. Az függvényt e háromszögön belül kell bizonyos peremfeltételek mellett megkomponálni (Czimber 2002).
A „diszkrét elemes modell” kifejezés gyűjtőnév, számos számítógépes eljárás sorolható ide. Akkor nevezünk egy mechanikai modellezési technikát diszkrét elemes modellnek, ha egyrészt igaz rá, hogy a vizsgált testet egymástól egyértelműen elkülönülő elemekből építi fel (mint a falazat téglái, vagy a száraz homoktalaj szemcséi), másrészt képes egyenként szimulálni minden egyes ilyen elem mozgását és az elemek egymással kialakuló érintkezéseit, egymástól való elválását, egymásra hatását. Eltérően tehát a végeselemes modellektől, ahol az elmozdulásmezők a végeselemek érintkezési pontjaiban különféle folytonossági követelményeket teljesítenek, a diszkrét elemes modellekben az elemek önálló elmozdulásokra képesek, akár úgy is, hogy nem is érintkeznek egymással. Továbbá amíg a szokásos kontinuum-mechanikai alapú keret- vagy törésmechanikai szoftverek legfeljebb az elemek közötti kapcsolatok megszűnését tudják csak követni, egy diszkrét elemes modell az új kapcsolatok létrejöttét is az állapotváltozási folyamat szerves részeként kezeli. A diszkrét elemes modellek jelenleg még kutatás alatt állnak, de már most is találni építőmérnöki alkalmazását, mint pl. az aszfalt mikroszerkezetének vagy a vasúti ágyazat tömörödésének vizsgálatát. A diszkrét elemes modellezésről az érdeklődő olvasó további hasznos információkat kaphat Bagi Katalin (2007) A diszkrét elemek módszere című munkájában.
Az imént felsorolt – összetett számításokat igénylő – méretezési eljárások támogatására az elmúlt évek folyamán különböző számítógépes szoftverek jelentek meg és kerültek alkalmazásra (DAMA, LAYMED, CHEV5L, BISAR, ELSYM5, ALISE, APPROX-5RET stb.). Ezen programok többsége azonban nem a véges elemek módszerét alkalmazta, hanem a jóval egyszerűbb közelítő eljárásokkal éltek az AMADEUS kutatás jelentése szerint. Ennek legfőbb oka az lehet, hogy bár a bonyolult „nagy programok” a rugalmasságtan határain belül mindent tudnak és megadnak, a Hooke-törvény linearitásának feltételezésével mégis a valóságos útpályaszerkezet viselkedését csak nagyon közelítő módon, jó becslésszerűen modellálják és írják le. A mechanikán alapuló méretezési módszerek bár jelentős fejlődés előtt állnak, mégis számos problémával kell szembenézni alkalmazásuk esetén. Gondot jelent ugyanis az anyagállandók meghatározása, valamint a fáradási és deformációs jelenségek leírása. Ez fokozottan van érvényben gazdasági utak esetében, ahol is sokszor költségcsökkentés miatt nem szabványos anyagok kerülnek beépítésre és a jellemző technológiai fegyelem sem túl magas. Ennek köszönhetően a tervezés alatt feltételezett és az építés alatt megvalósított paraméterek, modulusok nagymértékben eltérnek egymástól.
Hivatkozások
Czimber K. (2002): Geoinformatika. Elektronikus jegyzet, Sopron, p. 101.
Bagi K. (2007): A diszkrét elemek módszere, BME Tartószerkezetek Mechanikája Tanszék
http://www.sciencedirect.com/science/article/pii/S0950061811007720
http://www.geomechanics.ethz.ch/research/Inverse_analysis/
