CWA15846 Dinamikus tömörségi-fok elmélete és módosításának háttere
Bevezető, előzmények
A dinamikus tömörségmérés egy új fogalom, a tömörségi fok mérése alakváltozás mérésével és nem sűrűségarány meghatározással történik. A már közel tíz éves mérési adatok és tapasztalatok alapján a módszer véglegesítése lehetségessé vált. Pontosabb, gyorsabb, olcsóbb, mint a korábbi módszerek. Környezetbarát, az Unióban kiváltani tervezett izotópos mérés utódja lehet. Az új elmélet térfogat-elemzésen alapul, melyet e bejegyzés mutat be részletesen .
Az új magyar elmélet a talaj térfogatcsökkenését süllyedés-méréssel, ejtősúlyos terhelési módszerrel, 10-18 ejtéssel létrehozott tömörödési görbéből határozza meg és egyben a dinamikus teherbírási modulust is méri. A B&C (Bearing Capacity & Compaction-rate Tester) ezért 2in1 dinamikus mérési módszer. Mivel a tárcsa alatti terhelés a statikus terhelésnél alkalmazottal egyező, az Ed=E2, azaz nem kell átszámítás.
A mérési módszer megjelent ÚT 2-2.124 Útügyi Műszaki Előírásként 2005-ben, 2008-tól az uniós CWA15846 előírás szabályozza. E szabványt honosították Kínában, Japánban, Koreában, Új-Zélandon, Oroszországban, Brazíliában, az Európai tagállamokban Norvégiában, Hollandiában, Litvániában és számos más országban.
Az elmúlt évtized nagyszámú mérései, az elméleti tanulmányok, a nemzetközi verifikációk lehetővé tették a szabályozás véglegesítését, az összefüggések vizsgálatait valamint a tapasztalatok, beérkezett észrevételek alapján a módszer kiegészítését, pontosítását.
Proctor vizsgálat (V=constans modell)
Két fajtája terjedt el a világon, az egyszerűsített és a módosított. A standard (egyszerűsített) kisebb munkavégzéssel, míg a módosított (nagyobb tömörítési munkával) az EN 13286-2 szerint. V=constans modellnek azért nevezzük, mert a laboratóriumi vizsgálat kialakítása ilyen: levágjuk a tömörített mintát a Porctor-feltét eltávolítása után, emiatt a talajhenger-térfogat állandó, nedvességtartalma és száraz tömege a vizsgált pontonként eltérő. Meghatározzuk a víztartalmat és mérjük a tömeget. Számítjuk a talajminta nedves és száraz sűrűségét (1. ábra). Ekkor:
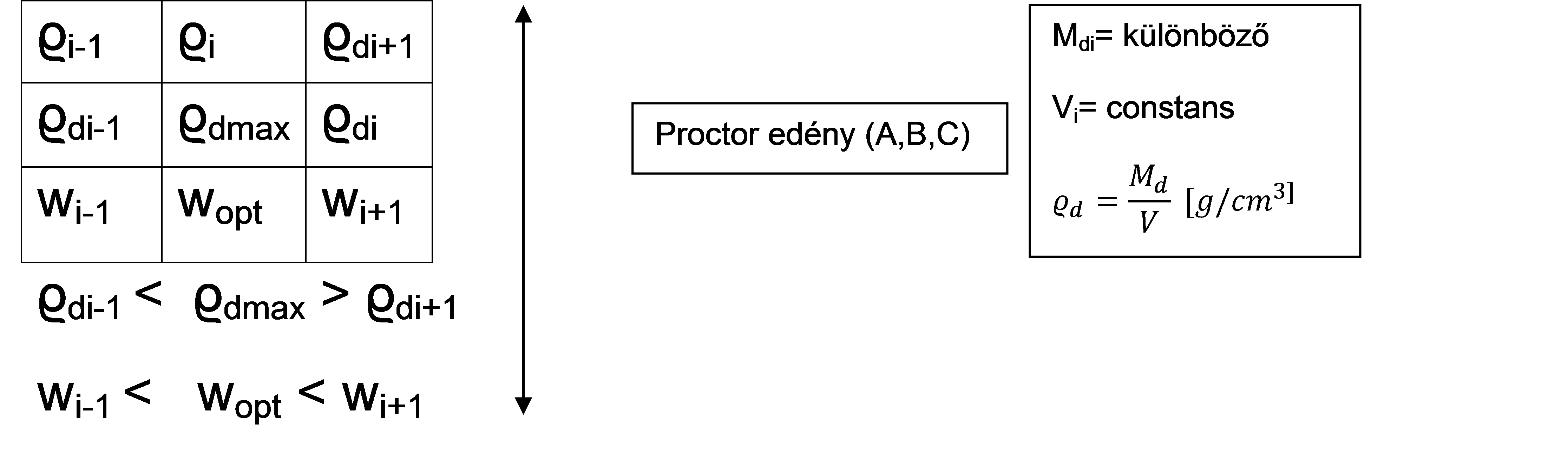 |
Proctor-vizsgálati minta térfogati összetétele wopt-nál (2. ábra):
 |
\[\frac{{\Delta}V_{a}}{A}={{\Delta}h}\]
ahol Δh a talajhenger tömörítési süllyedése (összenyomódása)
\[\frac{V_{opt}}{A}=\frac{V^{*}}{A}=h^{*}\]
ahol h* a tömörített henger magassága az optimális víztartalomnál
\[{\Delta}h=h_{i}-h^{*}\) → \(h^{*}=h_{i}-{\Delta}h\)
\[C_{rd}=\frac{V^{*}}{V_{i}}=\frac{A\dot{}h^{*}}{A\dot{}h_{i}}=\frac{h_{i}-{\Delta}h}{h_{i}}=\frac{h_{i}}{h_{i}}-\frac{{\Delta}h}{h_{i}}={1}-{\epsilon}\]
A dinamikus tömörségi fok (Dynamic Compaction-rate) = Crρ*100 (%). Levezethető fentiekből a térfogatváltozásból számított tömörségi fok és a sűrűségarányból megállapított tömörségi fok is: Crρ=V*ρdmax / V*ρdi = ρdmax / ρdi, ahol a tömörségi fok (Compaction-rate %) = Crρ*100 (%).
Proctor-vizsgálat (Md=constans modell)
Ha a száraz tömege minden Proctor-mintának azonos, akkor a magassága különböző lesz a különböző nedvességtartalmú tömörített talajhengereknek. A legkisebb magasságot az optimális víztartalomnál találjuk, magasabb lesz a henger a magasabb víztartalomnál és magasabb lesz a minta kisebb víztartalomnál is. Az optimális víztartalom a legtömörebb, legkisebb henger víztartalma, itt a Proctor tömörségi fok = 100%.
Ez a természetes szituáció a vizsgált talaj esetében a terepen is. A száraz talajsűrűség Md=constans, a víztartalma az esőtől, vagy a talajvíztől, talajpárától, vagy eredeti települési állapotától függő. A henger alatti tömörödés tehát csak a víztartalomtól függ (ha a tömörítési munkát rögzítettnek vesszük).
A talajhengerek mm-ben meghatározott magasság-különbsége (ahol a választott bázis az optimális víztartalmú minta magassága), úgy is tekinthető, mint tömörödési süllyedés és ehhez tudunk Proctor tömörséget rendelni.
Célunk az volt, hogy igazoljuk, a süllyedésekből is lehet számítani a tömörségi fokot (az adott tömörítő munka mellett mérve), nem csak sűrűség-arányokból.
 |
Következtetések
Legyen wi < wopt < wi+1 … a laboratóriumi Proctor vizsgálatnál sorrendben mért víztartalom. Feltéve, hogy henger Md=constans, és a tömörítési munka=constans, lehet számítani a térfogati összetevőket, a talajhenger magasságát. A választott bázis-térfogat önkényesen Vopt=2065,5 cm3 (Boussinesq feszültségeloszlás hatásmélységből ≈ 253 mm és a Proctor mintahenger alapterületéből a talajra átszámítva).
Vopt=Vmin és Vi>Vopt valamint ρdi < ρdmax és Mdi=Md*=constans
Vi > V*
* jelezzük a Proctor vizsgálathoz tartozó paramétert
Összefüggés vizsgálat (V térfogat =változó, Md=constans)
Md=constans állapot:
\[C_{r}=\frac{V^{*}}{V_{i}}=\frac{A\dot{}h^{*}}{A\dot{}h_{i}}=\frac{h_{i}}{h_{i}}-\frac{dh}{h_{i}}={1}-{\epsilon}\]
\[C_{r}=\frac{V^{*}}{V_{i}}=\frac{M_{d^{*}}/{\rho}_{dmax}}{M_{d_{i}}/{\rho}_{di}}=\frac{{\rho}_{di}}{{\rho}_{dmax}}\dot{}\frac{M_{d^{*}}}{M_{d_{i}}}=\frac{{\rho}_{di}}{{\rho}_{dmax}}\]
*jelezzük a Proctor vizsgálathoz tartozó paramétert
∆h a jele a magasság különbségnek a Vi és Vopt között, A=alapterület.
A két módszer tehát láthatóan azonos eredményre vezet, ha Md*=Mdi=Md=constans!
\[{C}_{r{\rho}}\%={C}_{rd}\%\]
 |
Ezzel igazoltuk, hogy a magasságkülönbségekből számított tömörségi fok egyenlő a sűrűségarányokból számított tömörségi fokkal.
Mintapélda: siSa, iszapos homok Proctor eredményei:
| w% | 8,9 | 10,9 | 11,1 | 12,5 | 13,9 |
| ρd | 1,99 | 2,06 | 2,06 | 2,01 | 1,96 |
Összefüggés a Δh magasságkülönbség és a Proctor tömörségi-fok között
Regresszió analízist végzünk a V=const Proctor vizsgálat eredményeiből
wopt → wi → V=2065,5cm3 Md=const=V*ρdmax h=252,9mm
ρdmax ρdi
Proctor edény “A”, döngölő “B” (EN 18286-2)
\[C_{rd}=1-{\epsilon}=100-{\Phi}\dot{}{{\Delta}h}\] ahol Φ=const=-0,380±0,02
Proctor munka = constans, a relatív tömörsége minden mintának \[C_{rE}=100\%\]
Dinamikus Tömörségi Fok (az optimális víztartalomnál)
\[C_{rd}\%=C_{rE}\%\dot{}T_{rw}\]
ahol \(T_{rw}=(MCC)\) Moisture Correction Coefficient (nedvességkorrekciós tényező) \(T_{rw}=(MCC)=\frac{{\rho}_{di}}{{\rho}_{dmax}}\) és maximuma≡1.
A vizsgálati eljárás tehát a következő:
- elvégezzük a módosított Proctor vizsgálatot,
- számítjuk az Md=conts modell-állapotot (referencia térfogat 2065,5cm3), wopt-nál,
- meghatározzuk az összes Proctor pont térfogati adatait,
- meghatározzuk a Δh-Trρ% értékeket víztartalmanként,
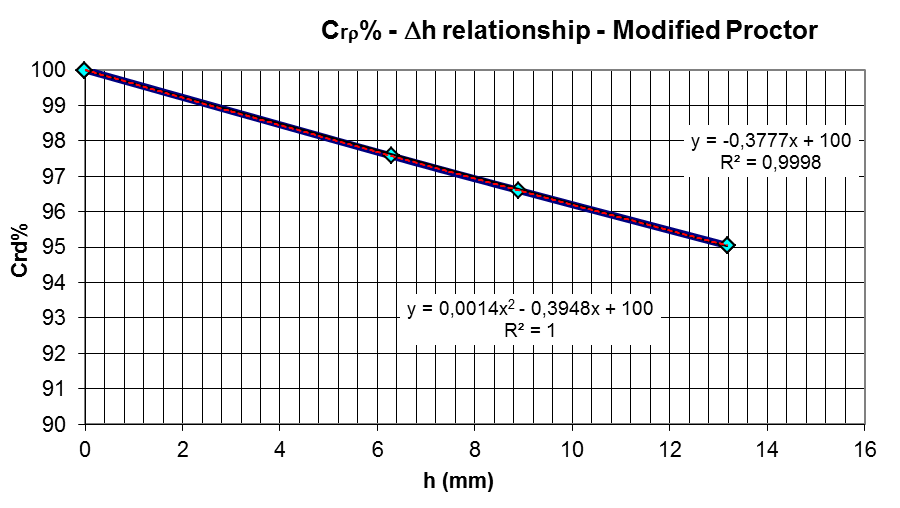
- meghatározzuk Φ értékét, ami a regressziós egyenes meredeksége.
A regressziós egyenes (lásd 4. ábra) általános alakja Crd=100-Φ*Δl, nem-linearis alakja (polynom) Crd=(100-0,014Δl2-0,39Δl). Ez utóbbi azt mutatja, hogy a minimális helyszíni relatív tömörségi fok legkisebb értéke 71% körül van.
Terepi tömörség mérés (B&C)
A süllyedés számítható a Boussinesq-képletből különböző Ei felvett modulusokra. A laboratóriumi körülmények különböznek a helyszíni méréstől. A hatásmélység miatt, a feltételezett (tárcsa alatti) talajhenger magassága különböző. Ez az arány:
\[\frac{H_{eff}}{H_{pr}}\cong{1,25}\]
A több mérőeszköznél használt Light Falling Weight (LFW) terhelési módszer jelen esetben azon az elven alapul, hogy leejtünk kb 10 kg tömeget 72 cm-ről, ezzel terheljük a talajfelületet p=0,35 MPa tárcsa alatti terheléssel D=163 mm átmérőt használva. Gyorsulásmérőt és kvarcórát használva meghatározhatjuk a süllyedést:
\[S=\frac{a}{t^{2}}\]
| ahol | |
| \(a\) | gyorsulás mértéke m/sec2, |
| \(t\) | terhelési idő (sec). |
CEN WA 15846 előírása szerint teljes sorozatnál 18 ejtés szükséges és ezek a süllyedések csökkenést mutatnak az ejtések számának növekedésével. A süllyedések különbsége felfogható úgy, mint állandó (maradó) alakváltozás. Ilyen módon, az összegzett süllyedések az elejétől az aktuális ejtési számig az adatsorból számíthatók. Mivel a süllyedések nagysága csökkenő, a súlyozott átlaga ezeknek adja az eredő süllyedést, mint eredményt, elosztva 17-tel a súlyozott summa adatsorok összegét.
\[{\Delta}s=s_{i}-s_{i+1}\]
A számítás elmélete: ejtés számával súlyozott átlag Ds süllyedésekből (deformációból)
\[{\Delta}s_{1}+{\Delta}s_{2}+ … +{\Delta}s_{i}=\sum_{i=1}^{i=17}{\Delta}s_{i}\]
minden adatsorban számítva:
| Ejtés száma/Süllyedés | Maradó süllyedés | Summa delta süllyedés | Ejtésszámmal súlyozva N°=di |
| 1/ 2,47 mm | |||
| Δs1 | SUMΔ1 | 1*SUMΔ1 | |
| 2/ 1,74 mm | |||
| Δs1+Δs2 | SUMΔ2 | 2*SUMΔ2 | |
| 3/ 1,14 mm | |||
| Δs1+Δs2+Δs3 | SUMΔ3 | 3*SUMΔ3 | |
| …. | |||
| SUM Δsi | SUMΔi | i*SUMΔi | |
| 17/ 0,80 mm | |||
| \[\sum_{i=1}^{i=17}{\Delta}s_{i}\] | SUMΔSUMΔi | Δ=1-17 | |
| 18/ 0,75 mm | |||
Az így súlyozott átlag neve a Deformációs mutató (Dm) limitált értéke 3,0. Nem értékelhető a tömörség-mérés a szabvány szerint ha Ed<10MPa és Dm>3, mert ekkor nem jött létre elegendő deformáció, a süllyedési görbe egyenes és nem csökkenő. Lágy felületen a leejtett súly nem tudja tömöríteni az elterített réteget. A tömörítő henger sem. Ezeket a méréseket tehát nem megfelelőnek kell tekinteni.
Általánosságban a deformációs mutató számítása a következő:
\[D_{m}=\left[\sum_{i=1}^{i=17}{d_{i}}\dot{}\sum_{1}^{17}{SUM{\Delta}s}\right]\dot{}\frac{1}{17}\]
Ha ábrázoljuk ezeket az értékeket az ejtések számának függvényében, a süllyedési-tömörödési görbe második szakasza lineárishoz közelít, ezért 6-8 ejtés után lehet már becsülni a további süllyedési görbét. Ez a gyorsított tömörségi-fok mérés, minimum 10 ejtéssel, a 18 helyett. Ilyenkor a Dm (CrE%) értéke egy kicsit rosszabb, mint ha 18 ejtést végeztünk volna.
 |
A súlyozott tömörödési görbét a Dm pont reprezentálja. Minél nagyobb az ejtések száma, a súlya annál inkább érvényesülni fog. Ily módon a Deformációs mutató (Dm) definiálja a teljes összegzett süllyedéskülönbséget, egyetlen pontként.
Példa: ha Dm=22; akkor CrE%=100-1,25*0,380*22=89,55=90%
CrE% – Helyszíni relativ Tömörségi-fok (adott terepi víztartalom mellett)
CrE% a helyszíni relatív tömörségi fok (a CWA-ban TrE%-nak jelölve) – Ez az a mért érték, melyet az BC SP-LFWD kistárcsás dinamikus tömörség- és teherbírás mérő készülékkel az adott terepi víztartalom mellett mérünk, és ami reprezentálja a henger tömörítési hatékonyságát. Függetlenül az optimális víztartalomtól, ez:
\[C_{rE}\%=100-1,25\dot{}{\Phi}^{*}\dot{}D_{m}\]
ahol Φ* a módosított Proctor vizsgálat regressziós analíziséből származó meredekség értéke, és 1,25 az \(\frac{H_{eff}}{H_{proct}}\) aránya.
A CWA 15846 előírja a Φ érték ellenőrzését. Ha a Φ értéke és a különbsége nagyobb, mint a megadott intervallum, akkor a mért tényleges (Proctor-vizsgálattal meghatározott) Φ értéket kell alkalmazni a számításban. (Ilyen eset nem volt az eddigi gyakorlatban). A választott meredekség értéke Φ*.
Nedvesség Korrekciós Tényező (MCC Moister Correction Coefficient)
Ahhoz hogy megkapjuk a tömörségi-fokot, transzformálni kell a mért CrE% helyszíni relatív tömörségi fokot az optimális víztartalomra. A „normalizált” Proctor-görbét használjuk, mely az adott víztartalom melletti száraz sűrűség és a maximális száraz sűrűség hányadosa.
Dinamikus tömörségi-fok (CWA 15846 SP-LFWD)
Megszorozva a CrE% helyszíni tömörségi-fok értéket (a természetes víztartalommal mérve) a Trw%=(MCC)=Moister Correction Coefficient=nedvességkorrekciós tényezővel transzformáljuk azt az optimális víztartalomra. Ebből következik, hogy a BC mérés CrE% eredménye mindig ≥ Trd% értéke, attól függően, hogy a terepi víztartalom mennyire tér el az optimálistól (lásd 6. ábra).
\[T_{rd}\%=T_{rw}\dot{}C_{rE}\%\] és \[T_{rd}\%=T_{r{\rho}}\%\]
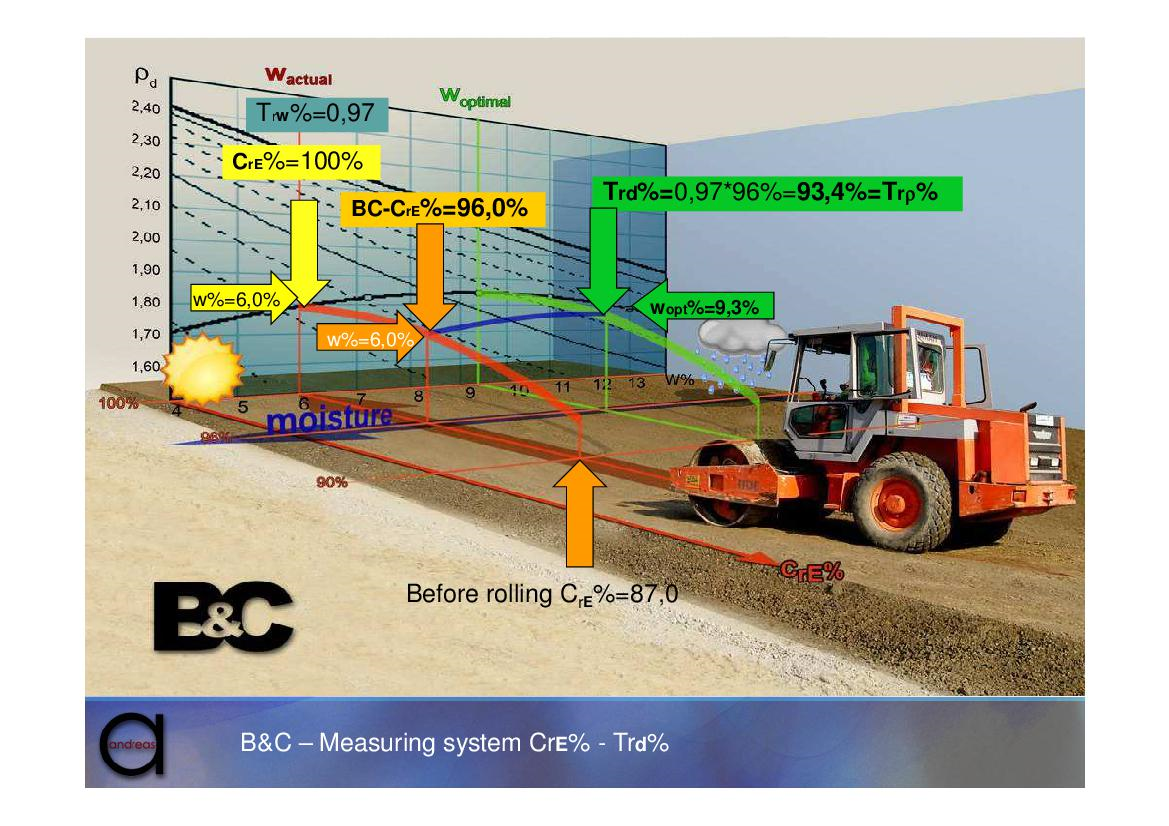 |
A hatásmélység vizsgálata (Boussinesq)
Az eddigiekben azt feltételeztük, hogy a talajréteg vastagsága állandó. A CWA módosítása azonban lehetővé teszi, hogy bármilyen rétegvastagságnál végrehajthassuk a dinamikus tömörségmérést. Bevezettük ezért az IDP fogalmát.
IDP (Impact Depth Multiplier) hatásmélység szorzó, mely a rétegvastagság figyelembevételére szolgál.
Példa: \[IDP=\frac{{\Phi}_{20}}{{\Phi}_{25}}=\frac{0,4739}{0,3802}\cong{1,25}H_{eff} < stress 20\% = constans\]
különböző E talaj-modulusok esetén egyformán, mert attól független.
Proctor Φ értéke függ a mért réteg vastagságától. Nincs szükség rétegvastagság korrekcióra, ha a rétegvastagság 22-28cm közötti és elfogadjuk a Φ=0,380 TrE%=±1% mérési pontosságot. Nincs szükség korrekcióra, ha a rétegvastagság 20-31cm közötti és elfogadjuk a Φ=0,380 TrE%=±2% mérési pontosságot. Minden más esetben korrekció szükséges:
| CrE% | Heff/Hproct | cm | Φ |
| +2% | 1,25 | 20 | 0,474 |
| +1% | 1,14 | 22 | 0,431 |
| 0% | 1,00 | 25 | 0,380 |
| -1% | 0,89 | 28 | 0,340 |
| -2% | 0,81 | 31 | 0,308 |
A biztonság javára az IDP=1,25 (lásd a CWA 15846-ban) ami az építési gyakorlatban alkalmazott 20-25cm névleges terítési rétegvastagságnak megfelelő.
Vastagsági korrekció minden más esetben:
LTC (Layer Thickness Correction) rétegvastagság korrekció figyelembe vétele:
Φ=Φkorr=LTC*Φ* ahol Φ*=0,380 vagy Φ=Φkom=9,1185*h-0,9871 ahol h a rétegvastagság cm-ben
 |
Az elégséges tömörítő munka ellenőrzése
CWA15846 meghatározza a rétegvastagság határokat, biztosítva a pontosságát a dinamikus tömörség-mérésnek. Számos esetben lehet azonban a terített réteg vastagabb, vagy egyszerűen csak tudni szeretnénk, hogy a BC mérésnél alkalmazott tömörítési munka elégséges volt-e, vagy sem. Ebben a helyzetben az eljárási szabály a következő:
Végre kell hajtani egy újabb tömörség mérést, a tárcsa elmozdítása nélkül. Ha az eredmény CrE% kisebb mint 98% lenne, akkor a következő munkavégzési korrekció (Control Work Coefficient) számítása és alkalmazása szükséges:
\[CWC=Control\ Work\ Coefficient=\frac{C_{rE}\%}{100}\]
Ez a CWC érték csökkenti a Trw nedvességkorrekciós tényező értékét:
\[T_{rwCorr}=T_{rw}\dot{}CWC\] és ily módon \[T_{rd}\%=C_{rE}\%\dot{}T_{rwCorr}\]
Ezzel a dinamikus tömörségi fok mérése függetlenné vált a rétegvastagságtól, mert az figyelembe vehető. (Maximális rétegvastagság értelemszerűen legföljebb a hatásmélység lehet.)
Korrekciók alkalmazása
Korrekció az impulzus-törvény miatt:
Az ejtősúlyos terhelési módoknál a mért dinamikus modulust korrigálni kellene az impulzustörvény miatt. A nagytárcsás LFWD-k, a KUAB és Dynatest méréseknél is, a mért pályaszerkezeti réteg (talaj) térfogatsűrűségétől (víztartalom, anyagsűrűség, tömörség) függően. Úgy találtuk, hogy korrekciót általában a teherbírás értékére el kell elvégezni (Ed). Korrekciót mindig kell számítani a pernyére, kohósalak esetén vagy más, nagy sűrűségű anyagok esetén.
Sűrűségi korrekció tömörségre és teherbírásra az impulzustörvény alapján (pernye):
Átszámítás: \[{\varsigma}_{E}=\frac{{\rho}_{1}(1+w_{1})}{{\rho}_{2}(1+w_{2})}\dot{}\frac{100}{T_{rE}\%}\]
m = 0,986·TrEmért% – 98,7 és TrEszám% = 100+m·ζ
Példa: Mért értékek: Ed = 18,9 MPa, TrE% = 91,7%, wt = 38,3%.
Nedves sűrűség: 1,26 g/cm3; wopt = 26%; Trw = 0,985; Proctor: ρdmax=0,91 g/cm3.
(A mért statikus teherbírás ugyanott E2 = 37MPa, Tt = 1,6; kiszúró-hengeres tömörségi fok Trρ = 98,3% volt).
ζ = (0,91*1,26)/(1,65*1,07) = 1,147/1,766 = 0,649; m = (TrEmért%*0,986) – 98,7 = –8,3
TrEszám% = 100 – 8,3*0,649 = 94,6% és Trw = 0,985
TrdKORR% = Trw*TrE% = 0,985*94,6 = 93,2%
Teherbírás: Edkorr = Ed*(1/ζ)*(100/Trd%) = 18,9*(1/0,649)*(100/93,2) = 18,9*1,54*1,07 = 31,1 MPa (E2=29,2MPa), azaz pernye esetén a teherbírás értéke magasabb lett.
Sűrűségi korrekció teherbírásra kohósalak esetén:
Ed KORR = Ed*K ahol K= 1.766/ (ρdmax*1/(1+wopt))
Példa: ρdmax = 2,28; wopt = 12,2; K = 1,766/2,032 = 0,87 , ha Ed = 86,6, akkor Edkorr = 0,87*86,8 = 75,5 MPa, azaz kohósalak esetén a teherbírás értéke magasabb.
Tömörítési munka ellenőrzése: (vagy >29 cm rétegvastagaság esetén) a következő:
A tömörségmérés (18 ejtés) után újabb 18 ejtéses mérést végzünk, de a tárcsa elmozdítása nélkül. Ha a második mérés eredménye CrE2%<98%, akkor korrigáljuk a korábbi mérési eredményt; ha nagyobb, vagy egyenlő akkor elfogadjuk a korábbi mérési eredményt korrekció nélkül:
\[CWC=\frac{C_{rE2}\%}{100}\] és \[T_{rwK}=CWC\dot{}T_{rw}\]
Átszámítás az egyszerűsített (standard) Proctor tömörségi fokra (Német területen használt):
A CWA15846 szerinti dinamikus tömörségi fok a módosított Proctor-vizsgálatot alkalmazza (Trwértékében). Az egyszerűsített (standard) tömörségi fok ebből a következőképpen számítható:
\[{\beta}=\frac{{\rho}_{dmax\ simplified}}{{\rho}_{dmax\ modified}}\] és \[T_{rd\ simplified}\%=\frac{1}{\beta}\dot{}T_{rd}\%\]
Az átszámításhoz mindkét Proctor vizsgálat elvégzése szükséges ugyanabból az anyagmintából.
Trd% standard = Trd% (1/β) ahol β = (ρdmaxSt /ρdmaxMod);
Példa: Trd% = 95% ρdmaxS t= 1,82 woptSt = 13,5% ρdmaxMod = 1,96 woptMod = 13,5%; β = 0,943
Trd% standard = 1/0,943·95% = 101%
Regresszió analízis eredményei
Az elvégzett mérések nagyszámú mintáinak feldolgozásából a különböző mérések között fennálló összefüggések megállapítására is lehetőség nyílott. Az összehasonlítások előtt a CWA15846:2015 módosítási javaslat alapján korrigáltuk az adatokat, majd az összefüggéseket elemeztük.
E2v – Ed összefüggés
A statikus teherbírási modulus E2v≅Ed vagy E2v=1,0*Ed R2=0,8, azaz E2 közel azonos mint az SP-LFWD-vel mért Ed érték. A regresszió szorossága kifejezetten jó. Ez azt jelenti, hogy a BC mérés hasznos teherbírást mérő eszköz lehet az építőmérnöki gyakorlatban. A D=300mm tárcsaátmérőjű statikus tárcsás vizsgálat és a BC Dinamikus Tömörség- és Teherbírás mérés számszerűen egyező értéket mutat (8. ábra). A figyelembe vett tolerancia a statikus tárcsás mérés eredményekben ±5MPa, míg a CWA 15846 Ed értékeknél ±2,6MPa a 8. ábrán bemutatva (58 próbabeépítés, 763 mérés). A méréseket független, akkreditált laborok végezték.
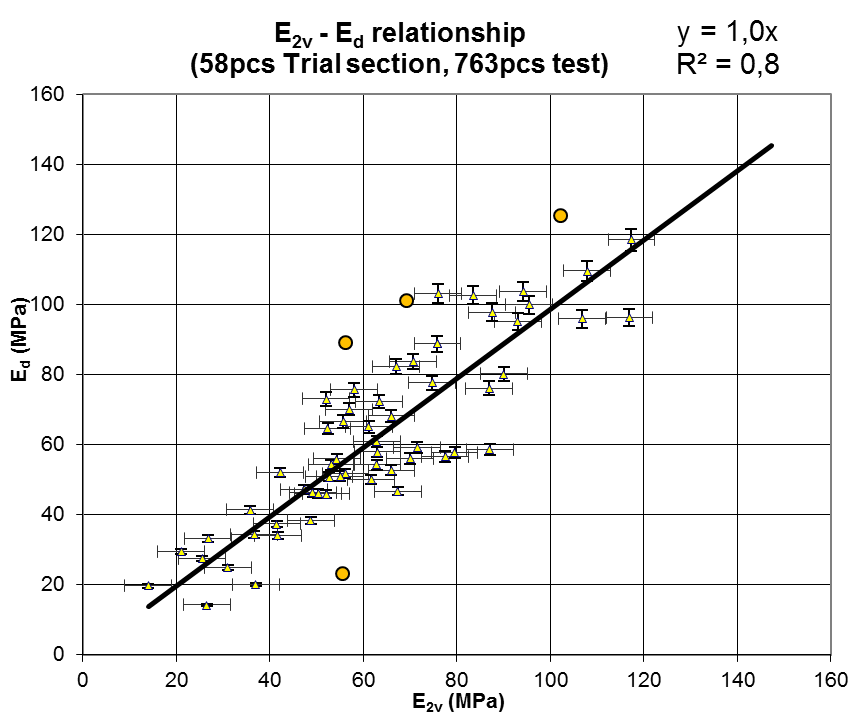 |
Izotópos és dinamikus tömörségi fok
A Trd% dinamikus tömörségi fok egyenlő az izotópos (vagy más sűrűségi arányon alapuló) tömörségi fokkal.
\[T_{rd}\%=T_{r{\rho}}\%\] (R2=0,7)
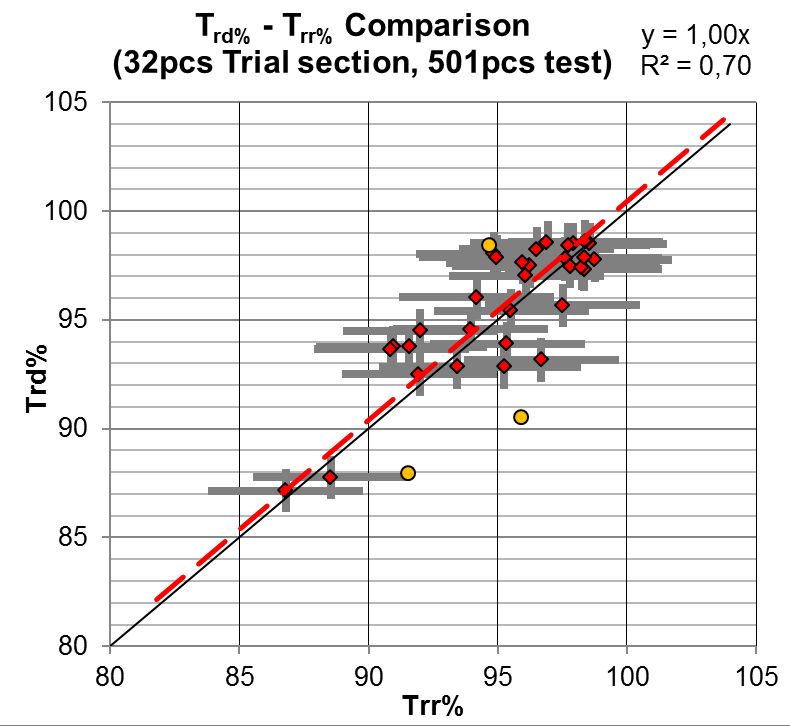 |
A regresszió szorossága meglehetősen jó. Ez azt jelenti, hogy a BC készülék hasznos tömörségi fok mérő műszer lehet az építőmérnöki gyakorlatban. A méréseket MC-3 izotópos mérőeszközzel és BC-1 Dinamikus tömörség- és teherbírás mérő berendezéssel végezték független, akkreditált laborok. A figyelembe vett optimista tolerancia az izotópos mérésnél optimistának nevezhető ±3Tr% , míg a CWA 15846 szerinti dinamikus tömörség mérésnél ±1Trd%. Az összefüggést a 9. ábrán mutatjuk be.
Homok-kitöltéses tömörségi fok (AASHTO) – Dinamikus tömörségi fok
Az összehasonlítást a RAMKHAMHAENG University, Bangkok Thailand Department of Civil Engineering Tanszéke végezte el. (Comparison of B&C LFWD and sand filling method –Ramkhamhaeng University, Thailand Ms.Panarat-Mr Korrakoch Taweesin: Calibration Certificate B&C, Gabor Enterprise CO Ltd. 2007). Az összehasonlító méréseket egy mérési szakaszon 30-30 darab mérésből átlagolták, eredménye:
\[T_{rd}\%=T_{r{\rho}}\%\]
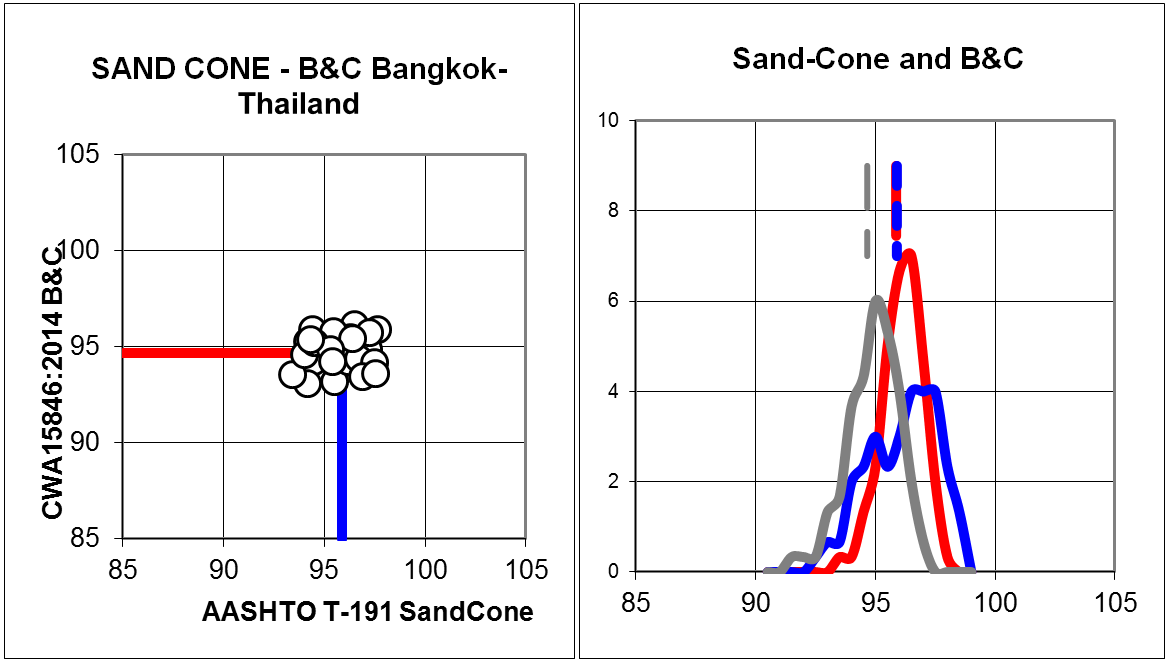 |
AASHTO T-191 Homok-kitöltéses és a CWA15864 dinamikus tömörségi fok összehasonlítás (Bangkok-Thailand) N=30-30 darab méréssel, azonos mérési szakaszon és rétegen történt. A szórás a homok-kitöltéses mérésnél s=1,40, tömörségi fok átlaga 95,9%. A szórás a CWA15846 SP_LFWD mérésnél a kedvezőbb s=1,13 tömörségi fok átlaga 95,9% (azonos) volt. A szürke vonal a CWA15846 módosítás utáni dinamikus tömörségi fok értékeket jelöli, az eltérés jelentéktelen -1Trd% körüli (mérési pontosságon belüli érték).
ÁTSZÁMÍTÁSOK ÖSSZEFÜGGÉSEK ALAPJÁN
A számos próbabeépítés, külföldi tanulmányok és ezek vizsgálati eredményei lehetővé tették, hogy egyéb összefüggéseket is vizsgáljunk és megfelelően szoros korreláció esetén megadjuk ezeket. A dinamikus tömörség- és teherbírás mérés így hasznosabb lehet, több információ nyerhető.
Várható süllyedés a töltéstestben visszatöltésben, alaprétegben (ha a tömörségi fok idővel a mért tömörségi fokról 100%-ra változik) ΔS=ΔTrd% /4,75 (mm/25cm-es rétegre).
Példa: ha 90%-ról a tömörség 100%-ra változik, akkor 10/4,75=2,1 mm/25 cm réteg, azaz 8 m magas híd-háttöltés esetén a tömörödés 8*4*2,1 mm=6,70 cm
Dinamikus ágyazási tényező
A BC mérés első mérési sorozatából meghatározható dinamikus ágyazási tényező, mely alapok alatt, ipari csarnokok padlóburkolatai tervezési előírásainál használatos.
\[c_{d}=\frac{0,071}{S_{0a}}\ (N/mm^3)\]
ahol S0a = (ejtés No. 1 + 2 + 3) / 3 (mm) Regresszió szorossága R2=0,92
Példa: ha S0a =1,33 mm akkor cd =0,0761/1,33mm=0,06N/mm3
BOMAG Evib értéke BC dinamikus teherbírás mérésből: Evib=0,5*Ed+57 (R2=0,93)
Evib CCC-method (University of Ljubljana) Példa: ha Ed=86,8MPa akkor Evib=100,4 Mpa
Német nagytárcsás LFWD Evd
Evd = 0,42*Ed (R2=0,90), vagy Evd = 0,69 Edend ((R2=0,91) a kisebbik a kettő közül. Példa: Evd=0,42*Edend=0,42*131,6=55,3 MPa; Evd=0,69*Ed=0,69*86,8=59,9 MPa; a kisebb: Evd=55,3MPa
Dinamikus CBR%
CBR5=5,43/s0a ;CBR2,5=4,07/s1a ; CBR% súlyozott átlaga e kettőnek. A CBR% számításának választott módja különbözik a szokásostól, mivel a terhelési görbe eltérő a statikus teherbírás mérés és a dinamikus teherbírás mérés esetében. A súly a CBR5–nek és a CBR2,5–nek a CBR% meghatározásához a mért s0a és s1a amplitúdóktól függ. A figyelembe veendő súlya a CBR5–nek= 1-(s0a/(s1a+s0a)); míg a CBR2,5–nek = 1-(s1a/(s1a+s0a)). A súlyok összege 1. A választás és a módszer a dinamikus tömörödési görbe jellemzőit tükrözi természetes úton következtetve és egy egyedi módszer a súlyozás megválasztásával.
Példa:
ha s0a=1,33mm és s1a=0,47mm, akkor
CBR5=5,43/1,33=4,1% ; és
CBR2,5=4,07/0,47=8,7%;
CBR5 súlya=(1-(s0á/(s1á+s0á))= 0,231;
CBR2,5 súlya= (1-(s1á/(s1á+s0á))=0,739; összegük=1,0 CBR%=4,1*0,231+8,7*0,739=CBR%=7,5%
ÖSSZEFOGLALÓ
CWA15846 szerinti dinamikus tömörségmérés alkalmazása megbízhatóbbá teszi a minőségellenőrzést és emeli a földmunkák, szemcsés rétegek építésének megbízhatóságát. Lehetővé teszi, hogy a tömörségmérés eredménye sokkal pontosabb és megbízhatóbb minősítési módszert kínáljon. Az új dinamikus tömörség- és teherbírás mérési módszer megteremti a Kivitelező – most nem létező – önellenőrzési lehetőségét is, melyet az ISO 9001 előír. Súlyos garanciális költségeket lehet megelőzni az önellenőrzéssel és sok meghibásodást. Jelenleg a kivitelező vakon dolgozik, szokás alapján tömörít.
A két nagyon különböző mérést (tömörségi-fok és teherbírás mérés) egyetlen BC könnyű-ejtősúlyos mérőeszközzel lehet végrehajtani a CWA15846 szerint. Míg az ára a BC készüléknek nem éri el a két különböző hagyományos berendezések (MC-3 és E2 statikus teherbírás mérő) együttes árának felét, fenntartási költségei is jóval alatta maradnak az izotópos készülék üzemeltetési költségeinek.
A CWA 15848 szerinti dinamikus tömörség mérés lényegesen pontosabb, mint az izotópos mérés, ezért annak helyettesítésére kellene alkalmazni, a környezetet és az egészséget szükségtelenül veszélyeztető, sőt terrorveszélyesnek minősített izotópos mérőeszköz helyett.
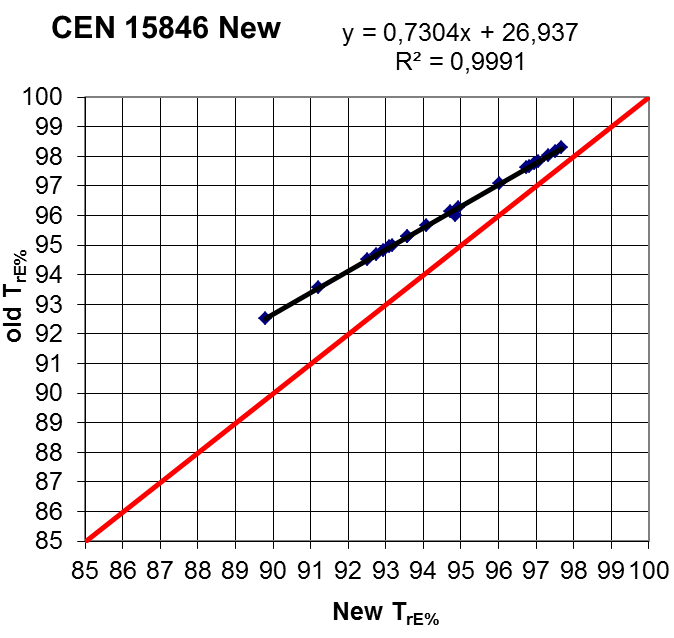 |
Megvizsgáltuk a CWA15846 módosításának hatását vizsgálva az elemzés azt mutatta, hogy a különbség az új és a régi TrE% között 90 % tömörségi foknál -2,5TrE%, ugyanez TrE=95%-nál vagy e felett kevesebb mint 0,5TrE%, azaz kevesebb mint a mérési hiba (TrE% ≈1TrE%).
A véglegesített CWA mérési szabvány (és a benyújtott ÚT 2-2.124 ÚME) alkalmas az eddig használt izotópos tömörség és teherbírási határértékek megtartására, módosításuk nélkül.
A tömörségi és teherbírási előírásokat nem kielégítő alapréteg, visszatöltés, vagy földmunka az épített szerkezet meghibásodáshoz vezethet, mely mindig és jól láthatóan megbosszulja magát. A nem megfelelő alapok, beszakadások, süllyedések utólagos javítása igen nehéz.
Autópályáinkon, közútjainkon gyakran látjuk viszont a deformációt, a megsüllyedést, az építés alatti minősítő mérések „megfelelősége” ellenére. A B&C berendezés és elméletének kifejlesztése lehetővé tette a korrekt minőségtanúsítást, a kivitelezők önellenőrzését és a pontatlan izotópos mérés kiváltását.
Irodalomjegyzék
[1] CWA15846:2008 Measuring method for Dynamic Compactness & Bearing Capacity with SP-LFWD (Small – plate Light Falling Weight Deflectometer) modification draft. p.26
[2] MSZ 2509-3:1989 Útpályaszerkezetek teherbíró képességének vizsgálata. Tárcsás vizsgálat.
[3] MSZ 15320 Földművek tömörségének meghatározása radioizotópos módszerrel
[4] MSZ15846 Dinamikus tömörség- és teherbírás mérés kistárcsás könnyűejtősúlyos berendezéssel (kidolgozás alatt)
[5] ÚT 2-2.124 Dinamikus tömörség- és teherbírás mérés kistárcsás könnyűejtősúlyos berendezéssel
[6] ÚT 2-3.103 Radiometriás tömörségmérés. Földművek, kötőanyag nélküli alaprétegek hidraulikus
kötőanyagú útalapok térfogatsűrűségének és víztartalmának meghatározása
[7] Dr Kézdy Á. Talajmechanika I. 1972. Tankönyvkiadó p.74-94, 388-403.
[8] Dr Kézdy Á. Talajmechanika II. 1975. Tankönyvkiadó p.153-163, 175-196.
[9] D.Adam, F.Kopf (2004) Operational devices for compaction optimization and quality control (Continuous Compaction Control & Light Falling Weight Device). Proceedings of the International Seminar on Geotechnics in Pavement and Railway Design and Construction, Rotterdam.
[10] Brandl, H. and Adam, D. (2004) Basics and Application of the Dynamic Load Plate Test in Form of the Light Falling Weight Device. A.W. Skempton Memorial Conference. Proc. of Imperial College, London.
[11] Anna Petkovsek (2008) Report on usage of Andreas dynamic load bearing capacit ity of Ljubljana Katedra za mehaniko tal z laboratorijem. Univerza v Ljubljani Faculteta za gradbenistvo in geodezijo. Report p.:10
[12] Ms. Panarat (2007): Comparison of B&C LFWD and sand filling method Ramkhamhaeng University, Thailand. Calibration Report
[13] Subert (2015) Földmű tömörségi inhomogenitás lehetséges hatása az utak új IRI egyenetlenségi követelményének teljesíthetőségére. Ráckevei 25. Jubileumi Geotechnikai Konferencia. 2015 október 12-14
[14] Subert (2015) CWA15846:2008 Modification Draft and Main Background Studies. Engineering Geology – Rock Mechanics 2015 Congress. BMGE Hungary. p.:379-394
[15] Subert (2014) Isotope-free Compaction-rate & Bearing Capacity Measure on Lime Stabilization – Self control. Article and Presentation. Carmeuse Conference. 09 sept 2014 Vecsés, Hungary p.:10
[16] Subert (2014) Izotópmentes tömörség- és teherbírás mérése – Önellenőrzés. 2014EPB Konferencia Gyergyószentmiklós, Románia, p:14, á 6.
[17] Subert: Measuring Methods of Compactness-rate & Bearing Capacity in Europe. 18th International Conference on Civil Engineering and Architecture, p:281-284. 12-15 june 2014 Csiksomlyó (RO)
[18] Subert-T.Q.Phong (2009) Az izotópos és a dinamikus tömörség szórásának vizsgálata. Transport Science Bulletin / Közlekedéstudományi szemle apr p:23-27.
[19] Subert (2009) A tömörségi fok átszámítása az egyszerűsített és módosított Proctor vizsgálatok között”. Transport Science Bulletin / Közlekedéstudományi szemle jun-2009 p:23-28.
[20] Subert-T.Q.Phong (2007) Proctor-vizsgálat új értelmezési lehetőségei. Revue of Roads and Civil Engineering / Közúti és mélyépítési szemle, ISSN 1419-0702 , 57. évf. 12. sz. p.7-12.
[21] Subert (2006) Method for measuring Compactness-rate with New Dynamic LFWD. XIIIth Danube-European Conference on Geotechnical Engineering Ljubljana, Slovenia 2006, V.2. p:125-130.
[22] Subert I.(2005): „A dinamikus tömörség- és teherbírásmérés újabb paraméterei és a modulusok átszámíthatósági kérdései” Közúti és mélyépítési szemle 55. évf. 1. sz. p.28-32.
[23] Subert I. (2004) B&C dinamikus tömörségmérés Mélyépítés 2004 október–december p. 38–39
[24] Subert (2003) Dinamikus tömörség- és teherbírás-mérés könnyű-ejtősúlyos berendezéssel. Közúti és mélyépítési szemle 53. évf. N°5. p: 184-191.
[25] Subert (2014) CWA15846 WS33 – Background Investigations:
– Analysis of isotopic and the dynamic compactness rate’s deviation
– Application of density corrections in case of dynamic falling weight deflectometers
– Basic method & the effects for the CWA 15846 modifications
– Bedding Coefficient and CBR% calculation from CWA15846 test results
– Conversion of Compactness-rate Between Simplified, and Modified Proctor Test
– Effectiveness of earthworks qualification tests in Hungary
– ER-TRG01 Regulation for Trial Sections – Inspection System
– Example for Comparison the Accuracy the Isotopic- and the Dynamic Compactness Degrees
– Proctor vs BC Work
– Relationship of Φ and the Layer Thickness
