https://doi.org/10.36246/UL.2023.2.07
2023; 11. évfolyam, 18. szám
Pdf: Út-pályaszerkezet méretezése törés-elmélet alapján
Bevezetés
Az elmúlt két évtizedben megoldást kerestek a nagy teherbírású útpályaszerkezetek felső rétegeiben keletkező – elterjedt néven TDC, felülről jövő – repedések modellezésére. A több száz meghatározó kutatás eredményeként 2018.-ban az MEPDG méretezési módszert is továbbfejlesztették. 2018. év előtt kezdődő projektek keretében a törésmechanikán alapuló viszkoelasztikus repedés képződési modellt dolgoztak ki, amit felhasználtak [1] a TDC repedések előrejelzésére.
A merevségi gardienst sok tényező, többek között a hőmérséklet, a terhelési idő vagy frekvencia, a kötőanyag öregedése és a terhelési ciklusok száma, az anyag fáradása befolyásolja.
A MEPDG továbbfejlesztésének keretében [1] kidolgozott modellek segítségével véges elem módszerrel 194400 futtatást végeztek, amely futtatások eredményét betanították a mesterséges neurális hálózati ANN modellnek. Az ANN modell két rejtett rétegekben 60 db neuront alkalmaztak. A kimeneti réteg és a két rejtett réteg aktiválási függvényei a közismert lineáris függvények és log-szigmoid függvények. A betanított program segítségével már „egyszerűen” meghatározható a repedés helye, mélysége, súlyossága és terjedésének sebessége.
A neurális hálózati ANN modellek olyan eseteket is képesek „felismerni”, amelyeket nem tanítottunk be, de olyan paraméterek hatását nem tudja kezelni, amelyek a betanítás során, mint bemeneti adatok hiányoztak, pl. a nem mért szilárdsági adatok.
A repedések terjedésnek számításánál a rugalmas képlékeny törésmechanikai elveket használják. Feltételezik a repedés jelenlétét, – ami az út-pályaszerkezetben adott a hézagok miatt – és számítják a repedés terjedéséhez szükséges képlékeny alakváltozási munkát. Az elméletet döntően fémekre és viszonylag homogén anyagokra dolgozták ki. Az elmélet kidolgozása Paul C. Paris nevéhez fűződik ezért szokták nevezni Paris módszernek is.
A tanulmány célja igazolni, hogy a rugalmassági modulus gardiensének ismerete szükséges, de nem elégséges feltétele a mechanikai méretezési módszer megbízható alkalmazásának. Az elégséges feltétel kielégítéséhez még ismerni kell a pályaszerkezeti rétegek húzó és nyomószilárdságának gardiensét. Bizonyítom, hogy az út-pályaszerkezeti rétegek együtt dolgozását is biztosító ragasztóanyagot – bitumen filmet – is út-pályaszerkezeti rétegként kell számításba venni, amely réteg hatása a pályaszerkezetben keletkező feszültségek szempontjából nem elhanyagolható, sőt jelentős.
A tanulmányban a töréselméleten alapuló új út-pályaszerkezet méretezési módszert mutatok be.
Töréselmélet, mint lehetséges méretezési eljárás
A felülről jövő repedések okaiként számtalan tényezőt szoktak felsorolni [2, 3] pl. a terhelés a gumiabroncsok alatt nem egyenletes, a terhelés nem kör alakú, nem egy tárcsa terhel, az abroncs szélénél jelentős nyírófeszültség alakul ki, a felső aszfaltréteg rugalmassági modulusa az oxidáció miatt gyorsan növekszik, ahol először kialakul a repedés ott várható a repedésterjedés gyors növekedése stb. Az okok átfogó és teljes körű elemzésével többek között az MEPDG fejlesztését megalapozó tanulmányok is foglalkoznak [1].
A hagyományos Magyarországon is alkalmazott méretezés szerint a repedések az út-pályaszerkezeti réteg alján keletkeznek és innen terjednek felfelé, amíg kialakulnak a hálós repedések az útburkolat felszínén.
Az út-pályaszerkezeti rétegek rugalmassági modulusának ismeretében számíthatjuk az alsó rétegben keletkező feszültségeket és fajlagos megnyúlásokat. A számított fajlagos megnyúlást összehasonlíthatjuk a tapasztalaton alapuló megengedhető megnyúlásokkal, ami alapján dönthetünk az út-pályaszerkezet megfelelőségéről a terhelő forgalom ismeretében.
Ez a mértezési módszer általában jól használható „E” forgalmi terhelési osztályig.
A hagyományos méretezésnél azért feltételezzük, hogy a repedés az út-pályaszerkezete aszfaltrétegének alsó síkban keletkezik, mivel aszfaltkeverék nyomószilárdsága jóval meghaladja a húzószilárdságát.
A feltételezés másik oka, hogy a nyomott oldalon a normál főfeszültségek különbsége húzott oldalhoz képet kisebb, ezért a fő-nyírófeszültség is kisebb, ami csökkenti a repedés kialakulásának lehetőségét. A harmadik ok, hogy a törésmechanikában is általában azt feltételezzük, hogy a repedés terjedése a repedésre merőleges feszültségek a döntőek, az ilyen esetekre vannak jól kidolgozott modellek.
Mindebből azt a látszólag logikus következtetést tudjuk levonni, hogy a felső rétegekben nem alakulhat ki repedés közvetlenül a forgalmi terhelés fárasztó hatása miatt. A továbbiakban igazolom, hogy a fáradási repedés az alsó rétegek repedését megelőzően kialakulhat az út-pályaszerkezet felső rétegeiben is.
A felülről jövő TDC repedések számításakor is fontos a keréktárcsa modell típusa. Az analitikus számítási módszerek általában kör alakú tárcsával tudnak számolni, ezért saját modellben is evvel számoltam.
A terhelő erő 50 kN, a teher két kör alakú ikertárcsán oszlik el, a tehereloszlás nem egyenletes, hanem követei a gumiabroncs alatti eloszlást [3, 4]. A valóságoz közeli feszültségeloszlást eredményező közelítést kétszer öt tárcsával végeztem, ahol az ikertárcsák tengelyének távolsága 0,36 m.
Az egyik tengelyben központosan elhelyezett öt tárcsa elrendezése:
Sugár (mm) Terhelés (N)
115 8339
110 7629
95 5690
70 3090
20 252
Így az átlagos nyomás 0,63 MPa, a legalsó 115 mm sugarú tárcsa alatt kialakult nyomáseloszlást az 1. ábra szemlélteti.
 |
Az 1. ábra szerinti terhelésből eltérő vastagságú, az 1. táblázatban megadott, rétegekkel a tárcsa tengelyében számítottam az út-pályaszerkezetben keletkező feszültségeket.
Út-pályaszerkezetek típusai:
„A” típus „B” típus „C” típus
24 cm AC(1) 24 cm AC(1) 24 cm AC(1)
– 20 cm M60 20 cm Ckt-4
| Réteg neve: | Réteg jele: | Rugalmassági modulus (Mpa) | Poisson szám | Húzó-szilárdság su,t (kpa) | n= su,c/su,t |
| Aszfaltbeton | AC(1) | 4000 | 0,35 | 4000 | 2 |
| AC(2) | 2000 | 0,35 | 2000 | 2 | |
| Bitumenfilm | B(1) | 0,1 | 0,5 | – | – |
| B(2) | 4,0 | 0,5 | – | – | |
| Cementstabilizáció | Ckt-4 | 2500 | 0,25 | 700 | ~8-10 |
| Mechanikai stabilizáció | M60 | 300 | 0,4 | – | – |
| Felületi bevonat | FB | 200 | 0,35 | – | – |
| Altalaj | – | 86 | 0,5 | – | – |
Egy adott pontban a feszültségi főtengelyek irányában keletkező maximális és a minimális főfeszültségek ismeretében számíthatjuk a fő-nyírófeszültséget (1).
\[ τ_f=(σ_{max}-σ_{min} )/2 \]
ahol:
\( σ_{max} \) – a maximális normál főfeszültség kPa;
\( σ_{min} \) – a minimális normál főfeszültség kPa
Az 2. ábrán azonos terhelés mellett három különböző, ragasztás nélkül tökéletesen együttdolgozó – idealizált -, út-pályaszerkezetben keletkező fő-nyírófeszültséget ábrázoltam az egyik tárcsa tengelyében.
 |
Kétrétegű rendszerben, ahol a pályaszerkezeti réteg a 24 cm AC(1) aszfaltréteg, a \( τ_{max} \) legnagyobb fő-nyírófeszültség az aszfaltréteg alján keletkezik. Háromrétegű rendszerben, ahol az aszfaltréteg alatt 20 cm M60 mechanikai stabilizáció van, még mindig az aszfaltréteg alatt keletkezik a legnagyobb fő-nyírófeszültség. Ha azonban az M60 helyett Ckt réteget építünk a \( τ_{max} \) legnagyobb fő-nyírófeszültség az aszfaltrétegen belül 6 cm mélységben lesz, ez azt jelenti, hogy a \( τ_{max} \) legnagyobb fő-nyírófeszültség helye függ a pályaszerkezeti rétegek rugalmassági modulusainak arányától. Az is látszik, hogy az út-pályaszerkezet teherbírásának jelentős növelése – M60 mechanikai stabilizáció helyett Ckt-4 réteg – az aszfaltréteg alsó síkján jelentősen csökkenti a fő-nyírófeszültséget, addig 6 cm mélységben 168 kPa-ról 200 kPa-ra növekszik a fő-nyírófeszültség, amely egyben a legnagyobb fő-nyírófeszültség.
Egy út-pályaszerkezeten belül a \( τ_{max} \) legnagyobb fő-nyírófeszültség helye még nem jelenti a repedés megjelenése szempontjából kritikus helyet. Repedés, vagy folyás ott keletkezik, ahol a keletkező legnagyobb fő-nyírófeszültség meghaladja vagy eléri az út-pályaszerkezeti réteg nyírószilárdságát.
Egy út-pályaszerkezeti réteg nyírószilárdsága nem egy adott érték, hanem a normál főfeszültségek függvénye, pl. talajok esetén a Coulomb-féle egyenes, de hasonló összefüggés van a betonokra is, ami alkalmazható az aszfaltkeverékre is.
 |
Jelen tanulmányban a biztonság javára és az egyszerűbb tárgyalhatóság érdekében nem vettem figyelembe, hogy a Coulomb-féle egyenes nem egyenes, hanem egy burkoló görbe.
A talajmechanikában a Coulomb-féle egyenes meghatározását triaxiális vizsgálattal végezzük, ahol a \( c_{u} \) kohéziót, valamint a belső súrlódási szöget keressük, ahol a belső súrlódási szöget \(tanα\) – val fejezzük ki.
Olyan anyagok esetén, ahol a nyomószilárdság és a húzószilárdság viszonylag egyszerűen meghatározható célszerűbb a belső súrlódási szög kifejezése a (2) összefüggéssel, ahol az i. réteg belső súrlódási szöge.
\[ \sin \alpha_i=\frac{n_i-1}{n_i+1} ; n_i=\frac{\sigma_{u, c}^i}{\sigma_{u, t}^i} \]
ahol:
\( σ_{u, c}^i \) – i. réteg tiszta nyomáshoz tartozó nyomószilárdsága (MPa)
\( σ_{u, t}^i \) – i. réteg tiszta húzáshoz tartozó húzószilárdsága (MPa)
A nyomó, valamint a húzószilárdság vizsgálatánál nem szoktuk biztosítani, hogy a legkisebb főfeszültség 0 MPa legyen. Nem követünk el hibát a (4) nyírási hányados számításánál, ha a vizsgálatkori légköri nyomást 0 kPa-ra vesszük fel, de az így kapott 3. ábra szerinti \( σ_{u, i}^i \) ; \( σ_{u, t}^i \) , akkor alkalmazhatjuk az útpályaszerkezetben keletkező feszültségek számítási modelljében is a légköri nyomás 0 kPa.
Az út-pályaszerkezet egy pontjában keletkező feszültségállapotot 3. ábra szerint értelmezve a \( \sigma_1=\sigma_{max};\ \sigma_2;\ \sigma_3=\sigma_{min} \) főfeszültségekkel tudjuk jellemezni, ami egy feszültségi ellipszoid. Ebben a pontban, akkor következne be törés, vagy folyás, ha az (1) szerint számított \( \tau_f \) fő-nyírófeszültség elérné vagy meghaladná az i. rétegben a (3) \( \tau_u^i \) törési nyírófeszültséget, nyírószilárdságot.
\[ \tau_u^i=\frac{\sigma_{u,t}^i+\left(\sigma_{u,t}^i-\sigma_{max}-\sigma_{min}\right)\sin{\alpha_i}}{2} \]
\[ T_i=\frac{\tau_f}{\tau_u^i} \]
ahol:
\( T_i \) – az i. rétegre vonatkozó nyírási hányados.
A „ ”-t nevezem nyírási hányadosnak, amelynek reciproka biztonsági tényezőként is értelmezhető.
A „Τ” nyírási hányados szoros összefüggésben áll a várható fáradási élettartammal, a törést okozó terhelési ciklus számával, e tekintetben alapvetően eltér a módosított Mohr-Coulomb- féle töréselméletből levezetett biztonsági tényező értelmezésétől, ahol nem veszik figyelembe, hogy a töréshez tartozó belső energia a 3. ábra szerinti változó érték (3) a tiszta húzás és a tiszta nyomás között.A „hagyományos” \( \varepsilon_{eng} \) megengedhető megnyúláson alapuló méretezési módszer [5, 6] szerint, ami részben megfigyelésen alapul, az út-pályaszerkezetet terhelő forgalomhoz megadjuk a legnagyobb megengedhető fajlagos megnyúlás értékét \( \varepsilon_{eng} \) , általában \( 10^{-6} \) léptékben, és ezt hasonlítjuk össze a számított \( \varepsilon \) fajlagos megnyúlással.
Ez a módszer nem kompatibilis a törés elmélettel, mert nem számol az út-pályaszerkezeti rétegek szilárdságával, és figyelmen kívül hagyja, a terhelés tengelyével párhuzamos \( \varepsilon_z \) fajlagos alakváltozást, továbbá azt a tényt is, hogy a vizsgált, terhelésre merőleges X;Y síkban \( \varepsilon_x\neq\varepsilon_y \).
A megengedhető megnyúlás szerinti méretezési módszer nem számol az adott pont tényleges feszültségállapotával, ezért alkalmatlan a felső út-pályaszerkezeti rétegek leromlási ütemének előrejelzésére.A megengedhető megnyúlás szerinti méretezésnél az út-pályaszerkezet alsó síkján következik be a törés. Itt a függőleges nyomófeszültség már viszonylag kicsi ~50-150 kPa, szemben a radiális normál feszültséggel \( \sigma_r \).
A megengedett megnyúlás \( \varepsilon_{eng} \) és a radiális \( \sigma_{eng}^i \) megengedett normál feszültségre felírható a következő összefüggés, ha \( \varepsilon_{eng} \) a terhelése merőleges síkban minden irányban azonos:
\[ \varepsilon_{eng}=\frac{\sigma_{eng}^i-\mu_i\left(\sigma_{eng}^i+\sigma_z\right)}{E_{i\ }} \]
Átrendezve:
\[ \sigma_{eng}^i=\frac{E_{i\ }\varepsilon_{eng}+\mu_i\ \sigma_z}{\left(1-\mu_i\right)} \]
ahol:
\( E_i \) – az i. réteg rugalmassági modulusa (MPa)
\( \mu_i \) – az i. réteg Poisson száma
Számítható (2) szerint az \( \sigma_{eng}^i \)-hez tartozó megengedett fő-nyírófeszültség is.
\[ \tau_f^{eng}=\left(\sigma_{eng}^i-\sigma_z\right)/2 \]
Az i. rétegre vonatkozó megengedhető törési \( \tau_{eng}^i \) nyírószilárdságot az (6) összefüggést a (3)-ban alkalmazva:
\[ \tau_u^{i,\ eng}=\frac{\sigma_{u,t}^i+\left(\sigma_{u,t}^i-\sigma_{eng}^i-\sigma_z\right)\sin{\alpha_i}}{2} \]
A számíthatóság feltétele a rétegek nyomó és húzószilárdságának \( \sigma_{u,c}^i \) ; \( \sigma_{u,t}^i \) ismerete.
A méretezéshez szükséges megengedett nyírási hányados \( T_{eng}^i \) számítható a (7) és (8) hányadosaként a (4) szerint.
\[ T_{eng}^i=\frac{\tau_f^{eng}}{\tau_u^{i,\ eng}} \]
Méretezéskor az i. réteg, akkor megfelelő, ha a minden pontban teljesül, hogy a számított nyírási hányados \( T_{i} ≤ {T}_{eng}^{i} \) a megengedett nyírási hányadosnál kisebb vagy egyenlő.
Evvel a viszonylag egyszerű módszerrel a hagyományos legnagyobb megengedett megnyúláson \( \varepsilon_{eng} \) alapuló fáradási kritérium átvezethető a töréselméleten alapuló méretezésbe, ha mérjük a \( \sigma_{u,c}^i ; \sigma_{u,t}^i \) szilárdságokat.
Könnyen belátható, hogy a \( \varepsilon_{eng} \) nem lehet méretezési kritérium, mivel függ a \( \sigma_z \) terhelés síkjára merőleges fő feszültségtől, ami egy nagyon változó érték. Másként fogalmazva a \( \varepsilon_{eng} \), a \( \sigma_z \) normál feszültségtől függően okozhat törést, vagy folyást az út-pályaszerkezeti rétegben.
Az \( \varepsilon_{eng} \) megengedett megnyúláson alapuló méretezés elfogadható az alsó út-pályaszerkezeti rétegekre igaz, ahol a \( \sigma_z \) már viszonylag kicsi, „elhanyagolható”.
A másik elterjedt, Magyarországon is alkalmazott [7] méretezési lehetőség, a lefutott forgalmi terhelés miatt bekövetkező mért behajlások változásán, növekedésén alapul. Ekkor a valós tönkremeneteli folyamat ismerete nélkül azt tételezzük fel korábbi megfigyelések alapján, hogy \( TF_{m} \) mértékadó egységtengely forgalom után az útburkolat felszínén repedések jelennek meg. Ez a módszer egyáltalán nem tartalmaz mechanikai paramétereket a legnagyobb behajláson kívül, de legalább nem kelti azt a látszatot, mintha mechanikai alapú lenne a fáradási kritérium.Ilyen kritérium az UME [7]-ban megadott (10) hajlékony út-pályaszerkezeti rétegekre megadott fáradási görbe:
\[ S_{eng}=14,5TF_{m}^\frac{-1}{4,55} \]
ahol:
\( S_{eng} \) – megengedett behajlás (mm)
A nyírási hányados és az út-pályaszerkezetet „tönkretevő” (10) mértékadó forgalom összefüggés között is van összefüggés, amit a következő módszertan szerint határoztam meg, számoltam.
B-R forgalmi terhelési osztályokban „B” típusú, de különböző vastagságú aszfaltrétegek alján keletkező feszültségeket számoltam, amiből meghatározható a (4) nyírási hányados.
Terhelésként az 1. sz. ábrától eltérő a teherbírásméréskor alkalmazott – 50 kN, terhelés 150 mm tárcsa – dinamikus ejtősúlyos terhelést vettem figyelembe. Az út-pályaszerkezeten belüli normál feszültségek számításánál a 20 oC-os mértékadó aszfaltkeverék mechanikai tulajdonsága \( \sigma_{u,t} \)= 4,0 MPa, \( n_i=2 \); E=4000 MPa, figyelembe vettem az \( \frac{E}{\sigma_{u,t}} \) = állandó esetén, E=1205-7000 Mpa-ig a rugalmassági modulus változó hatását is.
A vizsgált aszfaltrétegek vastagsága változó E=1205-7000 Mpa rugalmassági modulus esetén 13; 15; 18; 21; 24; 27; és 31 cm.
Változatlan E=4000 MPa és \( \sigma_{u,t} \) = 4,0 MPa esetén az aszfaltvastagságok 11,5; 16,5; 22; 30; 41; 52 cm volt.
Az aszfaltréteg vastagságának megadásánál kiemelt szempont volt, hogy a (10) szerint eredményül kapott \( S_m \) mértékadó behajlás az UME [7] szerinti forgalmi terhelési osztályt jellemezze.Az FWD \( S_{din} \) dinamikus legnagyobb behajlás és a statikus mértékadó behajlás közötti összefüggés [8]:
\[ S_m=1,105{\ S}_{din} (10) \]
A „B” típusú út-pályaszerkezetre a 4. ábra szerinti \( {TF}_m \) mértékadó forgalom logaritmusa és a (4) \( T_{i} \) nyírási hányadosra logaritmusára \( TF_{m}>100\ 000\ et \) esetén a (12) összefüggést kaptam. A nagyon magas korreláció 20 oC-os hőmérsékleten minden esetben fennáll, ha a rugalmassági modulus és a húzószilárdság aránya \( \frac{E}{\sigma_{u,t}}=R \) állandó. Az R egy arányszám, amely a kezdeti, első terheléskori rugalmassági modulusa és annak törését okozó húzószilárdság közötti arányát fejezi ki. Az R az anyag ridegségét jellemzi, ezért nevezhetjük törékenységnek is.
\[ \log(T)=avlogTF_{m}+bv \]
A 2. táblázatban az UME-ban a hajlékony út-pályaszerkezetre megadott fáradási görbékre illesztett av; bv paraméterek találhatók az R törékenység függvényében. Ez azt jelenti, hogy a (10) legnagyobb behajlásból számított \( {TF}_m \) megengedett tervezési forgalom egyezik a (12) nyírási hányadosból számított \( {TF}_m \) megengedett tervezési forgalommal adott R törékenység esetén.
| R= | 667 | 1000 | 2 000 |
| av= | -0,4649 | -0,4756 | -0,5134 |
| bv= | 2,196 | 2,4539 | 3,0415 |
 |
A kérdés mekkora R mértékadó törékenység jellemzi az úthálózatot, ill. a felhasznált aszfaltkeverékeket.
Az \( \frac{E}{\sigma_{u,t}}=R \) törékenység állandó értéke a feltétele a magas 0,98 feletti korrelációnak, de nem ismerjük R pontos értékét.
A magas korreláció azt jelenti, hogy az UME-ban megadott (9) fáradási görbét egy állandó értékű törékenység \( R_m=\ \frac{1}{\varepsilon_m} \) jellemzi. Az UME-ban megadott fáradási görbe empirikus, ezért nem lehet egzakt, pontos képlettel meghatározni. Az UME fáradási görbe minden beépített aszfaltkeveréket egyszerre jellemzi, ezért az \( R_m=\ \frac{1}{\varepsilon_m} \) állandónak nagy a szórása, vagyis\( R_m=\ \frac{1}{\varepsilon_m} \) törékenység egy átlagos érték, amelyhez egy jelentős szórás is társul, hiszen minden eddig beépített aszfaltkeveréket jellemez. A probléma, hogy sem az átlagot, sem a szórást nem ismerjük, legfeljebb becsülhetjük.
Eltérő R törékenységű aszfaltkeverék illesztése a (10) fáradási görbére az av és bv 2. táblázat szerinti paraméterek változását okozza, amelynek következménye a fáradási görbe párhuzamos elcsúszása a 4. ábra szerinti illesztési egyenesen. Mivel a különböző R törékenységhez tartozó illesztési egyenesek regressziója közel azonos, ezért ezek az egyenesek fedésben vannak.
Az 5. ábrán már nem szerepel a (10) fáradási görbe alapján számított nyírási hányados összefüggés, amelyre illesztettük a különböző R eltérő törékenységű aszfaltkeverékeket. Az 5. ábrán már csak az eltérő R eltérő törékenységű aszfaltkeverékeket hasonlítjuk össze, amelyeket illesztettünk a (10) fáradási görbére, amelyek közül bármelyik lehet mértékadó aszfaltkeverék.
 |
A meglévő úthálózatot legjobban jellemző mértékadó törékenység \( R_m \) pontos értékének meghatározása további kutatást, vizsgálatokat igényel.
Ennek hiányában a mértékadó törékenységet \( R_m\ =1000 \) javaslom felvenni, amit korábbi hasító-húzó vizsgálatok eredményéből származtattam, amely közelítően jellemzi az 1980-2010-ig készült AB, JU, U, KAB, ÉHA aszfaltkeverékeket.
A mértékadó R törékenység értékének növelése csökkenti a biztonságot, míg csökkentése növeli a biztonságot, de növeli a szükséges aszfaltréteg vastagságát, amely növeli a költségeket.
Az R mértékadó törékenység hatását a következő példán lehet szemléltetni. Tételezzük fel, hogy a 4. ábrán a mértékadó tervezési forgalomhoz \( {TF}_m=7,2 \) \(10^{6} \) tartozó T=0,6 nyírási hányados feltételt az R = 2000 törékenységű aszfaltkeverék is teljesíti, vagyis ezt az aszfaltkeveréket tekintjük a mértékadó aszfaltkeveréknek. Ha tévedünk és a valós aszfaltkeverék törékenysége R = 1000, akkor a \( {TF}_m=6,45 \) \(10^{6} \), míg R =667 esetén \( {TF}_m=6,0 \) \(10^{6} \) egységtengely áthaladás, vagyis a tervezett út-pályaszerkezet tervezési élettartama kisebb lesz a tervezettnél.
Az 5. ábrából úgy látszik, mintha a nagyobb törékenységű aszfaltkeverék magasabb fáradási élettartamot eredményezne, de az 5. ábra csak azt mutatja, hogy R törékenység mellett mekkora az a mértékadó nyírási hányados, amely a megengedett tervezési forgalom \( {TF}_m \) lefutását biztosítja, ami egyben megfelel a (10) fáradási kritériumnak is.
Változatlan rugalmassági modulus mellett a \( \sigma_{u,t} \) húzószilárdság növelése, vagyis az R törékenység csökkentése arányosan csökkenti a nyírási hányadost. Adott fáradási görbe esetén (12) az aszfaltkeverék kisebb húzószilárdsága kisebb fáradási élettartamot okoz, míg nagyobb húzószilárdsága nagyobb fáradási élettartamot eredményez.
Röviden úgy is fogalmazhatunk, hogy a törékenység csökkentése kedvező, de azt is figyelembe kell venni, hogy a rugalmassági modulus csökkentése viszont növeli az út-pályaszerkezeten belül kialakuló feszültségeket, így a (3) \( \tau_f \) fő-nyírófeszültséget is.
Fontos megjegyezni, hogy a tiszta húzás szerinti \( \sigma_{u,t} \) húzószilárdság nem azonos a dinamikus hasító vizsgálatkor kapott ITS hasító-húzó szilárdsággal, amely vizsgálatot a vízérzékenységhez minden esetben elvégzünk [9]. Az eltérő módszerű vizsgálatokkal kapott szilárdsági eredményeket jelentősen befolyásolja a terhelés módja, sebessége, frekvenciája és a vizsgálati hőmérséklet.
A hasító-húzó szilárdság \( \sigma_{Hh} (ITS) \):
\[ \sigma_{Hh}=\ \frac{2F}{d\ h\ \pi} \]
ahol:
F – terhelő erő
(N)d – minta átmérője (mm)
h – minta magassága (mm)
A töréskor a terhelő erővel párhuzamos \( \sigma_z \) feszültség [11] is keletkezik, amelynek a terhelésre merőleges felületen, az eloszlása szinuszos. A \( \sigma_z \) feszültség eloszlásának elméletét Schleeh alapozta meg [21], a minta közepén a terhelési síkban kialakuló feszültség:
\[ \sigma_z=\ \frac{6F}{d\ h\ \pi}=3\sigma_{Hh} \]
Az elmélet ellenőrzésére, a feszültségeloszlás részletesebb vizsgálata érdekében véges elemes számításokat is végeztek [22], amely megerősítette a (13) összefüggést.
Töréskor a fő-nyírófeszültség (1) számítható:
\[ \tau_f=\ \frac{\sigma_{Hh}+\sigma_z}{2}=2\sigma_{Hh} \]
A tiszta húzáshoz tartozó \( \sigma_{u,t} \) húzószilárdság a (3) szerint az az ITS-ből a (12-14) alapján már számítható:
\[ \sigma_{u,t}=\sigma_{Hh}\ \frac{2\left(2-sin\alpha\right)}{1+sin\alpha} \]
A hasító-húzó szilárdságból számított \( \sigma_{u,t} \) húzószilárdság függ a belső súrlódási szögtől, n=1 esetén \( \sigma_{u,t}=4,0\ \sigma_{Hh} \), n=2 esetén \( \sigma_{u,t}=2,5\ \sigma_{Hh} \).
A BME aszfaltmechanikai kutatást [11] végzett, ahol 4 Hz terhelési frekvencián és 5 oC-os vizsgálati hőmérsékleten dinamikus hasító-húzó és dinamikus hajlító vizsgálatokat végeztek AB-20 és U-20 aszfaltkeverékeken. A próbatestek törését okozó húzó-hajlító szilárdsága és a hasító-húzó szilárdságának hányadosa 2,32 és szórása 0,11 volt, ami vizsgálati megerősítése (15)-nek. A tiszta húzás során mért húzószilárdság \( \sigma_{u,t} \) 2,32 szerese a \( \sigma_{Hh} \) hasító-húzószilárdságnak, ha n=2,28.
A nyírási hányados alapján történő méretezés esetén az út-pályaszerkezet akkor megfelelő, ha a mértékadó forgalom nagyobb vagy egyenlő, mint a tervezési forgalom \(TF_{m} \) ≥ TF, ahol közvetve felhasználjuk az eddig is alkalmazott (10) fáradási görbét (12) alapján.
A nyírási hányados és a legnagyobb megengedett behajlás alapján történő méretezés azonos eredményre vezet, ha nem vesszük figyelembe az aszfaltrétegek eltérő szilárdságát. Az azonosságot könnyen ellenőrizhetjük, ha adott út-pályaszerkezet és terhelés esetén számítjuk a (11) szerint \( S_m \) mértékadó behajlásból a (10)-ből kifejezhető \( {TF}_m \) mértékadó tervezési forgalmat.
A mértékadó behajlás számításakor ismert az aszfaltréteg alsó síkján a tangenciális \( \sigma_r \) és függőleges \( \sigma_z \) feszültségek, amelyekből meghatározható (1) a \( \tau_f \) fő-nyírófeszültség, valamint a (3) alapján a \( \tau_u \) nyírószilárdság hányadosa a T nyírási hányados. A nyírási hányados ismeretében (11)-ből kifejezhető a \( {TF}_m \) mértékadó tervezési forgalom, amely a legnagyobb behajlásból számított \( {TF}_m \) mértékadó tervezési forgalommal közel az R2=0,9933 regressziónak megfelelő eredményt fog adni.
Ez a magas regresszió minden esetben fennáll, ha a mértékadó törékenység \( R_m \) állandó. Az állítás megfordítása is igaz, vagyis az UME-ban megadott fáradási görbe egy olyan mértékadó aszfaltkeveréket jellemez, amelynél a törékenység \( R_m \) állandó.
Azt azonban tudjuk, hogy még azonos hőmérsékleten és/vagy terhelési frekvencián is aszfaltkeverékenként változik az \( \frac{E}{\sigma_{u,t}}=R \) a törékenység, ami jelentősen növeli a várható élettartam görbe szórását. Az UME fáradási élettartamra vonatkozó görbéi felülvizsgálatra szorulnak, de a továbbiakban a (10), mint etalont veszem figyelembe.
A nyírási hányadoson alapuló (12) méretezés nagy előnye, hogy a rugalmassági modulus mellett figyelembe tudjuk venni az út-pályaszerkezeti rétegek szilárdsági tulajdonságait is, ennek eredményeként nem csak az alsó út-pályaszerkezeti réteg várható tönkremenetelére vonatkozóan tudunk megbízható számításokat végezni, hanem bármely pontont, így a kopó és kötőrétegben is.
A jelentős különbséget a következő példával lehet szemléletessé tenni. Egy vasbeton födémet kell méretezni ismert teherre, az egyik esetben (10) a betonra és az acélbetétre csak a rugalmassági modulusát ismerjük, a méretezés ekkor csak és kizárólag a tapasztalaton alapul sok életveszélyes esetből kiválasztva a megfelelőket.
A másik esetben (12) megbízhatóan méretezünk az életveszély és az anyagi kár elkerülése érdekében, valamint a tartósság tekintetében felhasználva a korábbi megfigyelésekre vonatkozó tapasztalatokat (10).
A hagyományos legnagyobb behajláson és a töréselméleten alapuló kölcsönös megfeleltetés után térjünk vissza a töréselméleti megfontolásokra.
A törést, folyást okozó váltózó nyírószilárdság (3), miatt nem alkalmazhatók a közvetlenül Paris-féle modellek.
A \( \tau_u \) nyírószilárdság a Coulomb-egyenesen 3. ábra egy változó, ahol a fajlagos alakváltozási energiák is különböznek. Ez a tény a Paris modellben alkalmazva azt jelenti, hogy a repedés terjedéséhez szükséges alakváltozási munka nem egy állandó érték, hanem függ a feszültségállapottól is. Általánosan fogalmazva a test egy pontján kialakult repedés terjedéséhez szükséges fajlagos alakváltozási energia függ a feszültségi ellipszoidok alakjától – a főtengelyek méretétől – és irányától. Mindez abból a vizsgálati tapasztalatból következik, hogy az aszfaltkeverékek esetén több külső ill. belső munka kell a tiszta nyomással repedést kiváltani, mint tiszta húzás esetén, a két állapot között folyamatos átmenetnek kell lennie.
A fáradási folyamat törés mechanikai modellezésével jelen cikkben nem foglalkozom, de fontos megjegyezni, hogy a fáradási folyamat elemzésénél nem lehet figyelmen kívül hagyni, hogy a valós terhelésből eltérő időpontban keletkező fő-nyírófeszültségek irányai is eltérőek lesznek, mivel a terhelő gépkocsik nem egy vonalon haladnak. A fő-nyírófeszültségek a főirányokkal 45o-os szöget zárnak be, de még az abroncs tengelyében se teljesül az egyik főirány párhuzamossága az útfelületre merőleges tengellyel. Minél jobban eltérünk a terhelő kerék tengelyétől annál jobban eltér a 45o-os szögtől a fő-nyírófeszültség, ezt a feltételezést erősíti, hogy az olaszországi autópályák vizsgálatakor 20-40 fokot mértek [3] a TDC repedések irányára. A repedés szögét még a hűlés-melegedésből származó vízszintes normál feszültségek is befolyásolják. Minél kisebb a szög annál inkább termikus eredetű a repedés végső oka, amihez jelentősen hozzájárul a teherismétlésből származó fáradás. Az útburkolat felszínéhez közeledve a szög általában csökken, közelít a „függőlegeshez”, mivel itt a legnagyobb és leggyorsabb a hőmérséklet változása és itt keletkezik a legnagyobb termikus eredetű „vízszintes” normál feszültség és itt a legjelentősebb a kötőanyag öregedése. Többek között ezek az összefüggések okozzák a laboratóriumi fáradási vizsgálatok és a valós pályaszerkezet fáradási viselkedése közötti eltérést.
E rövid kitérő után térjünk vissza a (4) összefüggésre.
 |
A 6. ábra szerint az egyik tárcsa tengelyében a mélység függvényében számított nyírási hányados szemléletessé teszi a törés szempontjából kritikus helyeket. A törés, repedés ott következik be a legnagyobb valószínűséggel, ahol a nyírási hányados a legnagyobb, itt lesz a legkisebb a megengedhető \( {TF}_m \) tervezési forgalom (11). A törést okozó fő-nyírófeszültség (3) változása, csökkenése a 3. ábra szerint alakul a Coulomb egyenes mentén.
A fáradási méretezési ellenőrzést \( TF_{m} ≥ TF \) abban a pontban kell végezni, ahol a „T” nyírási hányados a legnagyobb.
A nyírási hányados értékét befolyásolja az \( \alpha_i \) belső súrlódási szög, valamit az R törékenység.
A T nyírási hányados az útfelületre merőleges tengely mentén 6. ábra szerint kialakult alakjára kis mértékben hat az „\(n_i\)” értéke, ill. az \( \alpha_i \) belső súrlódási szög, de a nyírási hányados értékét már jelentősen befolyásolja. Másként fogalmazva az „\(n_i \)” a nyómó és a húzószilárdság hányadosa a repedés szempontjából kritikus helyre alig van hatással, de a várható törés valószínűségét már jelentősen befolyásolja.Az „\(n_i \)” növelése csökkenti, míg csökkenése növeli a nyírási hányadost, avval fordítottan, de nem lineárisan arányos.A (2) alapján a belső súrlódási szög növekedése növeli az „\(n_i\)” értékét, így várakozásunknak megfelelően a nagyobb belső súrlódási szögű aszfaltkeverékek magasabb nyírási hányadost, nagyobb fáradási élettartamot eredményeznek, ha egyébként nem csökken a vizsgált réteg \( \sigma_{u,t}^i \) húzószilárdsága, pl. a megnövekedett hézagtartalom, bitumen „felesleg” és/vagy egyéb okok miatt, BBMT és SMA keverékek.
Az \( \frac{E}{\sigma_{u,t}}=R \) törékenység adott hőmérsékletre vonatkozik, ezért értéke változik a hőmérséklettel, terhelési frekvenciával. Ez különösen fontos alacsony hőmérséklet esetén.
A \( \sigma_{H,h} \) hasító-húzószilárdság és az \( E_{H,h} \) hasító modulus azonos irányban változik, növekszik vagy csökken egy adott paraméter változása esetén, pl. kötőanyag tartalom, vagy tömörség esetén egészen a Fraas-féle törésponttól + 40 oC hőmérséklet tartományban.
A \( \sigma_{H,h} \) hasító-húzószilárdság a kötőanyagra jellemző Fraas-féle töréspont környezetében eléri maximumát, míg a \( E_{H,h} \) hasító modulus tovább növekszik.
A Fraas-féle töréspont alatti hőmérsékleten a \( \sigma_{H,h} \) a hasító-húzószilárdság maximumának oka, hogy a próbatesten belül a kötőanyagban keletkező fő-nyírófeszültség meghaladja a kötőanyag nyírószilárdságát, így már a kötőanyag is törhet.
A kötőanyag merevsége, a nyírási modulusa a hőmérséklet további csökkenésével arányosan tovább növekszik, ezért a próbatest hasítási modulusa is nő, ami nagyon kedvezőtlen a fáradás tekintetében, mert az R törékenység hatványosan kezd növekedni.
Az UME (10) fáradási görbéje ezt a hatást is magában foglalja, amely további jelentős szórásnövekedést és méretezési pontatlanságot okoz.
A fáradási görbe szórása jelentősen csökkenthető, ha a törékenységet az \( R_m \) állandót évszakonként, vagy még pontosabban havonként határozzuk meg a forgalmi terhelés napszakára jellemző átlagos hőmérsékletet figyelembe véve és ennek megfelelően havi vagy évszaki fáradási görbéket alakítunk ki.
Ragasztóréteg hatása a keletkező feszültségekre
Az út-pályaszerkezeti rétegekben, különösen a réteghatáron keletkező legnagyobb nyírófeszültségre és a nyírási hányadosra nagyon jelentős hatással van a rétegeket összeragasztó anyagának vastagsága és rugalmassági modulusa is.
A 7. ábrán egy „hagyományosan idealizált” 24 cm vastag 4000 MPa merevségű aszfalt pályaszerkezetben keletkező az (1) szerint \( \tau_f \) fő-nyírófeszültségeket hasonlítok össze egy ötrétegű rendszerekkel, ahol van és nincs rétegtapadás. A ragasztott rétegek esetén a feszültségeket már csak a réteghatárokon számoltam.
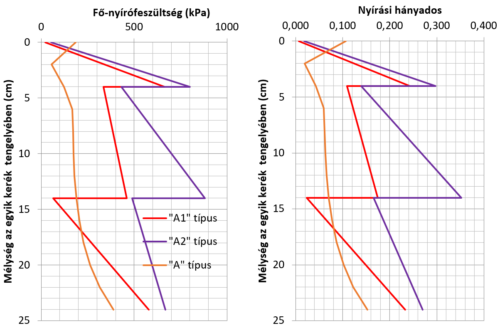 |
Út-pályaszerkezetek típusai:
„A” típus „A1” típus „A2” típus
4 cm AC(1) 4 cm AC(1) 4 cm AC(1)
0,2 mm B(1) 0,2 mm B(1), elvált
10 cm AC(1) 10 cm AC(1) 10 cm AC(1)
0,2 mm B(2) 0,2 mm B(2), elvált
10 cm AC(1) 10 cm AC(1) 10 cm AC(1)
Az „A” típus minden rétege egymással tökéletesen együtt dolgozik ragasztóanyag nélkül, ami egy idealizált 24 cm vastag AC réteget jelent – „A” típus.
Az „A1” és az „A2” típusoknál minden réteg között 0,2 mm vastagságú ragasztóanyagot, bitumen filmet feltételeztem.
A felső 4 cm kopóréteg és az alatta lévő 10 cm kötőréteg között a bitumen rugalmassági modulusa 0,1 MPa, míg a 10 cm kötőréteg és az alatta lévő 10 cm alapréteg között a bitumen rugalmassági modulusa 4,0 MPa. Az eltérést indokolhatja, hogy a kopóréteg alatt nyári napsütésben lényegesen melegebb a ragasztóanyag, mint a kötő és az alapréteg között, de az is előfordulhat, hogy a felső ragasztóanyag lágyabb, kisebb viszkozitású bitumenből készült.
Az „A1” és az „A2” típusoknál az eltérés az együttdolgozás tekintetében van, az „A1” esetén minden réteg együtt dolgozik, az „A2” esetén pedig nem.
Együttdolgozónak akkor tekinthetünk két réteget, jelen esetben az AC réteg és a ragasztóanyag között, ha a réteghatáron mindkét réteg fajlagos alakváltozása a réteghatár síkjában minden irányban azonos.
A két réteg nem dolgozik együtt, ha azok elváltak egymástól és a két réteg közé vízfilm kerül, ahol a feszültségállapot hidrosztatikus. Hidrosztatikus állapotban a feszültségek minden irányban egyeznek a terhelő irányú, „függőleges” feszültséggel. Az „A2” típus esetén még súrlódás sincs.
A 7. ábrán jól látható, hogy a ragasztott rétegek esetén már egyáltalán nem biztos, hogy a törés szempontjából kritikus hely az aszfaltréteg legalján 24 cm mélységben lesz. A kritikus hely függ a ragasztóréteg rugalmassági modulusától is.
Különösen fontos, hogy a 100 kPa rugalmassági modulusú ragasztóanyag alig javít az „A2” típushoz képest, ahol a rétegek nem dolgoznak együtt. Jelentős javulást a 4,0 MPa körüli rugalmassági modulus esetén várhatunk, amit a 8. ábra szemléltet a kötő és alapréteg közötti ragasztórétegre.
 |
Az út-pályaszerkezeti rétegeket összeragasztó bitumen, bitumenemulzió mechanikai tulajdonságait általában nem ismerjük, főleg nem ismerjük a hőmérséklettől a -5 oC – +15 oC hőmérsékleti tartományban, terhelési frekvenciától, oxidációs öregedéstől függését. Hazánkban más témakörben történtek vizsgálatok legalább a bitumen komplex nyírási modulusának meghatározására [12, 13].
Dinamikus nyíróreométerrel DSR 0,1 – 10 Hz körfrekvencia és a komplex nyírási modulus összefüggését vizsgálták [13] +60 oC-on, ahol a különböző típusú bitumenek mért komplex nyírási modulus 8 -200 kPa volt. Szintén DSR vizsgálatot végeztek eltérő tulajdonságú bitumeneken 1 másodperc felterhelési és 10 másodperc pihentetés mellett a komplex nyírási modulus meghatározására +40 oC – +60 oC között, a vizsgált bitumenek közötti akár ötszörös eltérés is lehet. A komplex nyírási modulus +40 oC-on 50 kPa – 200 kPa-ig terjedt.
A nyírási modulus jelentősen befolyásolja a nyírási hányadost 8. ábra, ezért a bitumen és a bitumen emulzió bitumen komponensének nyírási modulusát vizsgálni kell, és elő kell írni a bitumen megfelelő mechanikai paramétereit a megbízható, gazdaságos út-pályaszerkezet méretezéséhez. Bitumen esetén a rugalmassági modulus E = 3*G, ahol G a nyírási modulus.
A következőkben 9. ábra. a „C” típusú út-pályaszerkezeteket elemeztem, ahol az útalap Ckt-4 és a rétegek között már figyelembe vesszük a bitumenes ragasztóanyagot is „C1” és „C2”.
 |
Út-pályaszerkezetek típusai és tulajdonságai:
„C1” típus „C2” típus „D1” típus „E” típus
4 cm AC(1) 4 cm AC(2) 12 cm AC(1) 4 cm AC(1)
0,2 mm B(1) 0,2 mm B(1) 0,2 mm B(2) 0,4 cm FB
10 cm AC(1) 10 cm AC(1) 12 cm AC(1) 10 cm AC(1)
0,2 mm B(2) 0,2 mm B(2) 0,2 mm B(2) 0,4 cm FB
10 cm AC(1) 10 cm AC(1) 10 cm AC(1)
0,2 mm B(2) 0,2 mm B(2) 0,2 mm B(2)
20 cm Ckt-4 20 cm Ckt-4 20 cm Ckt-4 20 cm Ckt-4
A „C1” típusú és az idealizált „C” út-pályaszerkezetben keletkező nyírási hányados alapvetően és jelentősen eltér egymástól. A ragasztóanyag miatti jelentős nyírási hányados növekedés minden réteghatáron bekövetkezik a ragasztóanyag rugalmassági modulusának függvényében.
A „C2” típus esetén azt is vizsgáltam, hogy mi történik, ha a kopóréteg rugalmassági modulusa a felére csökken 4000 MPa-ról 2000 MPa-ra, amivel arányosan a húzószilárdságot is a felére csökkentettem, az törékenység változatlan maradt. A kopóréteg rugalmassági modulusának csökkenése – pl. a felső réteg hőmérsékletének növekedése miatt – nagyon kedvezőtlen, mivel megnövekszik a fő-nyírófeszültség, aminek következtében csökken a fáradási élettartam, és növekszik a TDC repedés megjelenésének valószínűsége. A TDC repedés nem feltétlenül fog a nyári melegben megjelenni, de a leromlott fáradás miatti húzószilárdság csökkenés a hidegben bekövetkező gyors lehűlési sebesség esetén nagyobb valószínűséggel éri el a termikus normál feszültség a lecsökkent húzó –és nyírószilárdságot.
SMA típusú kopórétegben, amelynek hasító-húzó szilárdsága ITS sok esetben 1,0 MPa körüli, a réteghatáron keletkező nyírófeszültség nagyon rövid időn belül elérheti, vagy meghaladhatja az SMA esetleg alacsony nyírószilárdságát.
Az UME-ban megadott fáradási modell és a (12) közötti összefüggés lehetőséget biztosít számunkra, hogy a húzószilárdság kiemelt jelentőségét szemléltessem a „C1” típusú út-pályaszerkezet kopórétegének alján keletkező feszültségből számított a nyírási hányados segítségével.
Mértékadó esetben a mechanikai paraméterek \( (\sigma_{u,t}^i \) = 4,0 MPa, \( n_i \) = 2; E=4000 MPa, R=1000) és pl. „E” forgalmi terhelési osztálynál a számított nyírási hányados T=0,216 és \( {TF}_m \) = 3,6 106 egységtengely áthaladás.Ha a \( \sigma_{u,t}^i \) húzószilárdságot 10%-al növeljük R=909, akkor T=0,197 és \( {TF}_m \) = 4,39 \( 10^{6} \) egységtengely áthaladás lesz, míg 10%-os csökkenés esetén R=1111 T=0,239 és \( {TF}_m \) = 2,92 \( 10^{6} \) egységtengely áthaladásra csökken.
A húzószilárdság 50%-os csökkenése esetén ( \( \sigma_{u,t}^i \) = 2,0 MPa, \( n_i=2 \); E=4000 MPa; R=2000), T=0,418 és \( {TF}_m \) = 0,90 \( 10^{6} \) az egységtengely áthaladás, így, ha a tervezés élettartama 20 év volt, akkor a kopóréteg felületén 5 éven belül – szavatossági időn belül – várhatók a repedések.
A „C1” típusú út-pályaszerkezetnél a kopóréteg alatt 100 kPa rugalmassági modulusú ragasztó réteggel számoltam, ha ezt 4000 kPa-ra növeljük – „C3” típus – pl. modifikált bitumenek alkalmazásával, akkor ( \( \sigma_{u,t}^i \)= 4,0 MPa, \( n_i \)=2; E=4000 MPa) esetén a számított nyírási hányados a kopóréteg alatt T=0,161 és a \( {TF}_m \) = 6,74 106 egységtengely áthaladás a duplájára növekszik.
A ragasztóréteg rugalmassági modulusát tovább lehet növelni „E” típusú pályaszerkezet ~ 200 MPa-ra egyrétegű 2/4 modifikált bitumenemulziós felületi bevonat alkalmazásával, hátrány a magasabb költség és a megnövekedett ragasztóréteg vastagság.
A 30-50 éve készült pályaszerkezetekből vett fúrt magmintákon azt tapasztaltuk, hogy a felületi bevonattal érintett rétegek fúráskor nem válta el egymástól. Az „E” típusú út-pályaszerkezet kedvezőbb a nyírási hányados szempontjából, mint a „C1” típus, de ez se ad kielégítő megoldást a magas költség ellenére, a ragasztóanyag nyírási modulusának növelése költséghatékonyabb megoldás.
Jó és gazdaságos megoldás lenne a kopó és a kötőréteg helyettesítése egyetlen 12 cm vastagságú aszfaltréteggel „D1” típus, ehhez azonban egy teljesen új eddig még nem alkalmazott, ismeretlen aszfaltkeveréket kell tervezni, amely nagy valószínűséggel drágább, de költséghatékony megoldás lenne.
A másik lehetőség ragasztóanyag nélkül „egyszerre” építeni a kopó és a kötőréteget, ez viszont egy teljesen új, hazánkban eddig még nem alkalmazott beépítési technológiára van szükség. Evvel a módszerrel a ragasztóréteg vastagságát lehet minimalizálni, hiszen ekkor már nincs szükség külön ragasztórétegre a ragasztás a keverékben meglévő bitumenfilm, bitumenes habarcs által jön létre, amelynek sokkal magasabb a nyírási modulusa, mint a ragasztáshoz használt bitumené.
A réteghatáron keletkező fő-nyírófeszültséget nemcsak a ragasztóanyag típusa, tulajdonsága, hanem vastagsága is befolyásolja 10. ábra. A nyírási hányadost a „C3; C4; C5” típusú 0,05 – 0,2 mm ragasztóanyag vastagságok esetén számítottam, ahol az út-pályaszerkezetek típusai és tulajdonságai:
| „C3” típus | „C4” típus | „C5” típus |
| 4 cm AC(2) | 4 cm AC(2) | 4 cm AC(2) |
| 0,2 mm B(2) | 0,1 mm B(2) | 0,05 mm B(2) |
| 10 cm AC(1) | 10 cm AC(1) | 10 cm AC(1) |
| 0,2 mm B(2) | 0,1 mm B(2) | 0,05 mm B(2) |
| 10 cm AC(1) | 10 cm AC(1) | 10 cm AC(1) |
| 0,2 mm B(2) | 0,1 mm B(2) | 0,05 mm B(2) |
| 20 cm Ckt-4 | 20 cm Ckt-4 | 20 cm Ckt-4 |
 |
A ragasztóanyag vastagságának csökkentése csökkenti a nyírási hányadost az aszfalt út-pályaszerkezeti rétegekben, ami növeli a fáradási élettartamot. A ragasztóanyag vastagságát lehet csökkenteni a kipermetezett ragasztóanyag mennyiségének csökkentésével, de ez nem vezethet a rétegtapadás elvesztéséhez.
A ragasztóanyag valós rétegvastagsága nem számítható a kipermetezett maradó bitumentartalom és a felület hányadosaként, hanem még figyelembe kell venni az aszfaltréteg fajlagos felületét, amit jellemezhetünk a makro-érdességgel. Minél érdesebb a felület annál nagyobb az a felület, amit a ragasztóanyaggal be kell vonni. A felületen a ragasztóanyag vastagsága még akkor se lesz egyenletes, ha a kipermetezés mennyisége tökéletesen egyenletes, mert a ragasztóanyag a lokális mélypontban összegyűlik, míg a magas pontokról lefolyik. A ragasztóanyag vastagságának egyenetlensége annál nagyobb minél nagyobb a makro-érdesség.
Tervezésnél a biztonság javára javaslom a 0,2 mm bitumen film rétegvastagság figyelembevételét.
Termikus feszültségek a nyírási hányados alapján
Az aszfaltok relaxációs képessége még hidegben is jelentős, ami azt jelenti, hogy a keletkező normál feszültségek viszonylag gyorsan leépülnek. A relaxációt avval az idővel jellemezzük, amíg a kezdeti normál feszültség a harmadára csökken. Ez az idő melegben néhány perc, de nagyon hidegben néhány óra is lehet. Melegben a termikus feszültségeknek azért nincs számottevő hatása mivel a hőmérséklet változása °C/perc lényegesen lassabb, mint a relaxációs idő, így alig keletkezik többlet normál feszültség.
Hidegben jelentős a relaxációs idő, amely már arányban áll egy gyors hőmérséklet-változással 5-10 °C/óra.
A \(T_{1} \) -től \( T_{2} \) -ig hőmérséklet változáskor az aszfalt út-pályaszerkezetben keletkező normál feszültség a következő képlettel számítható [14], ahol figyelembe vesszük relaxáció hőmérséklet függését is:
\[ \sigma_T=\sigma_0e^\frac{-t}{t_{rel\left(T\right)}}+E\left(T\right)\alpha\frac{t_{rel\left(T\right)}}{V}\left(1-e^\frac{-t}{t_{rel\left(T\right)}}\right) \]
ahol,
\( \sigma_0 \) – a már meglévő termikus normál feszültség (T-∆T) hőmérsékleten (MPa),
\( t_{rel\left(T\right)} \) – relaxációs idő a T hőmérsékleten (perc),
\( \alpha \) – hőtágulási együttható T hőmérsékleten (1/ °C),
\( E\left(T\right) \) – az aszfalt merevségi modulusa T hőmérsékleten (MPa),
\( V \) – a hőmérsékletváltozás sebessége (°C/perc),
\( t \) – a ∆T hőmérséklet változásának kezdetétől eltelt idő (perc).
Relaxaciós időnek \( t_{rel\left(T\right)} \) azt az időt nevezzük, amikor a kezdeti \( \sigma_o \) húzófeszültség \( \frac{1}{e}\sigma_o \)-ra csökken. A számítást ∆T hőmérsékleti lépcsőkben tudjuk elvégezni, ahol a kezdeti \( \sigma_0 \) =0. Ha pontosság rovására egyszerűsítünk és a t idő a hőmérsékletváltozás kezdetének és befejezésének a különbsége, akkor a \( V=\ t∆T \), és
\[ \sigma_T=E\left(T\right)\alpha∆TtrelTt1-e-ttrelT \]
A (17) összefüggés két részre bontható, egyrészről a közismert hőmérsékletváltozás okozta alakváltozás gátlásából származó normál feszültségre (19) és a relaxáció miatti csökkentő tényezőre (20).
\[ \sigma_h=E\left(T\right)\alpha∆T \]
\[ re=\frac{t_{rel\left(T\right)}}{t}\left(1-e^\frac{-t}{t_{rel\left(T\right)}}\right) \]
Mivel:
\[ t_{rel\left(T\right)}\le t\ és 1-e-ttrelT<0,632 \]
Ezért:
\[ re<0,632=1-\frac{1}{e} \]
Könnyű belátni, hogy minél kisebb az \( \frac{t_{rel\left(T\right)}}{t} \) hányados, annál kisebb az „re”.
Feltételezzük, hogy a mértékadó hőmérsékletváltozás sebessége „V” és időtartama „t” évszakonként nem változik, így a változó a \( t_{rel\left(T\right)} \) relaxációs idő minimuma magas aszfalthőmérsékleten, míg maximuma a legalacsonyabb hőmérsékleten van.
Ebből következik, ha a termikus feszültségek aszfalt útpályaszerkezet fáradására gyakorolt hatását akarjuk számolni, akkor a mértékadó relaxációs időt alacsony hőmérsékleten kell felvenni.
A legnagyobb a hőmérsékletváltozási sebesség V és legnagyobb hőmérsékletkülönbség ∆T a kopóréteg felszínén van. Minél mélyebb pályaszerkezeti rétegeket vizsgálunk, annál inkább csökken a sebesség és a hőmérsékletkülönbség. Ez az oka annak, hogy a kisforgalmú utakon, vagy a forgalommal nem érintett helyeken a termikus feszültségek miatti tönkremenetel elsősorban a kopórétegen jelentkezik 1. kép. Fúrt minták alapján általában azt tapasztaljuk, hogy a repedések a kötőrétegre már nem terjednek át.
 |
Mélyebb rétegekben, alapréteg a hőmérsékletváltozás sebessége 2-3 (oC/óra) csökken, szemben az útfelszíni ~ 10 (oC/óra) sebességgel.
A (18) és a (20) egyszerűsítés alapján a maximális termikus normál feszültség:
\[ \sigma_{Tmax}=E\left(T\right)\alpha\ ∆T 0,632 \]
Repedés akkor, jön létre a kritikus helyen, amikor a keletkező fő-nyírófeszültség meghaladja a nyírószilárdságot.
A maximális termikus normál feszültség kialakulásának feltétele, hogy \( t_{rel\left(T\right)}=t \).
A \( t_{rel\left(T\right)} \) aszfaltkeverék függő, míg a „t” az éghajlattól függ. A valódi kérdés az, hogy adott éghajlaton, hogy \( t_{rel\left(T\right)} \) idő alatt mekkora ∆T hőmésékletváltozásra számíthatunk, mi a mértékadó ∆T, amit a fáradás esetén alkalmazhatunk, és mekkora a ∆Tmax, amit az azonnali repedést okozó kritikus nyírófeszültség számításánál alkalmazhatunk?
A továbbiakban a kritikus nyírófeszültség számításával foglalkozom és egy példán mutatom be az alkalmazást -10 (°C) átlagos léghőmérsékleten.
Út-pályaszerkezet felépítése és tulajdonságai:
„C3” típus (-10 °C)
4 cm AC(3)
0,2 mm B(3)
10 cm AC(1)
0,2 mm B(3)
10 cm AC(3)
0,2 mm B(3)
m Ckt-4
T = -10 (°C),
α = -25.8 10-6 (1/ oC),
E(T) = 15 000 (MPa),
\( ΔT_{max} \) = 10 (°C) a burkolat felszínén,
\( ΔT_{max} \) = 7 (°C) 40 mm mélyen,
\( σ_{max} \) = 2 442 kPa (feszültség melegedés/hűlés esetén) a burkolat felszínén (23),
\( σ_{max} \) = 1 424 kPa (feszültség melegedés/hűlés esetén) 40 mm mélyen (23).
| Réteg neve: | Réteg jele: | Rugalmassági modulus (Mpa) | Poisson szám | Húzó-szilárdság su,t (kpa) | n= su,c/su,t |
| Aszfaltbeton | AC(3) | 15 000 | 0,2 | 9000 | 2 |
| Bitumenfilm | B(3) | 16* | 0,5 | – | – |
| Cementstabilizáció | Ckt-4 | 2 500 | 0,25 | 700 | 8-10 |
| Altalaj | – | 86 | 0,5 | – | – |
 |
A termikus húzófeszültséget hozzáadjuk a keréktárcsa terhelésből adódó vízszintes normál x,y irányú feszültségekhez \( \sigma_x\pm\sigma_{Tmax};\ \sigma_y{\pm\sigma}_{Tmax} \);\( \sigma_z \) és az így kapott feszültségekből számítjuk a 11. ábra szerinti fő-nyírófeszültségeket és a nyírási hányadost.
A számításokat a „C3” típusú út-pályaszerkezetre végeztem el, ahol a kopóréteg felszínén a felmelegedésből, míg a 4 cm mélyen a kopó és kötőréteg határán a hűlésből keletkező normál feszültség volt a mértékadó.
A nyírási hányados tekintetében külön vizsgáltam a hűlés és a melegedésből származó feszültségeket, amelyeket hozzáadtam a terhelésből adódó feszültségekhez. Az így kapott nyírási hányados változását tüntettem fel a 12. ábrán. A tehermentes állapotban a várakozásnak megfelelően a hűlés volt a kritikus állapot a kopóréteg felszínén és alján is.
A terheléssel együttes termikus feszültségeknél a kopóréteg felszínén a kritikus érték már nem a hűlésből, hanem a melegedésből származott. A kopóréteg felszínén akkor a legkedvezőtlenebb a nyírási hányados, amikor az út-pályaszerkezet még éppen terheletlen állapotban van, de a felterhelés már megkezdődött.
A repedés akkor jelenik meg, amikor a kopóréteg nyírószilárdsága annyira lecsökken, hogy a termikus normál feszültségek miatt keletkező fő-nyírófeszültség azt eléri vagy meghaladja.
A számítási mintában a 9,0 MPa a tiszta húzásból származó húzószilárdság, amely n=2,0 esetén 2,46 szerese a hasító húzószilárdságnak, amely ITS ~-3,6 MPa -10oC esetén.
A húzószilárdság is frekvencia és hőmérsékletfüggő, ezért a terheletlen állapotot úgy jellemezzük, hogy az egyezik a felterhelés kezdeti állapotával – még alig, vagy elhanyagolható a pályaszerkezetben keletkező feszültség -, de a terhelési frekvencia és hőmérséklet egyezik a teljesen felterhelt állapottal.
 |
A számítási eredmények azt sugallják, hogy a repedések biztosan a kopóréteg felszínén fognak megjelenni. Ez azonban a vizsgált „C3” típusú út-pályaszerkezetben csak és kizárólag akkor biztos, ha a kopóréteg aszfaltkeverékének építéskori húzószilárdsága -2,44 MPa, vagy a kopóréteg fáradási nyírószilárdság csökkenése a teljes vastagságban azonos.
A kopóréteg leromlása, fáradási üteme azonban nem azonos a függőleges tengely mentén.
A kopó-kötőréteg határán kialakuló nyírófeszültség ill. nyírási hányados lényegesen nagyobb, mint a kopóréteg felszínén, ezért a kopóréteg alján a fáradás gyorsabb.
A 9. ábrán a „C2” típus nyírási hányadosa a kopóréteg felszínén 0,133, míg az alján 0,336 vagyis 2,5 szerese.
A nyírási hányados szoros összefüggésben van a fáradási élettartammal, így a terhelés tengelyében a felszín leromlási üteme sokkal lassabb.
Ha viszont a számításokat nem a terhelés tengelyében, hanem a terhelő tárcsa szélének közelében 5-10 mm mélységben végezzük el, ahol a \( \sigma_z~0 \), szintén találunk a kopóréteg aljához hasonló, de annál kicsit kedvezőbb kritikus nyírási hányadost.
A kopóréteget terhelő forgalom felszíni imbolygása miatt a fáradás soha nem lesz homogén, ezért a törés következményeként előálló repedés a kopóréteg bármely részén kialakulhat, de legnagyobb valószínűséggel a kopóréteg alján és/vagy felszínének közelében lesz.
A termikus eredetű feszültségeknek nemcsak egy rövid idejű maximuma, hanem létezik egytartós értéke is, amely több órán keresztül megmarad, nagyon lassan épül le és nem szoktuk a leépülésnek ezt az idejét mérni.
 |
Ez a tartós termikus húzófeszültség:
\[ \sigma_{Ttart}=E\left(T\right)\alpha\ ∆T k \]
ahol:
\( k\le0,368\)
A ∆T hőmérsékletkülönbség akár több óra időtartamra is vonatkozhat, ezért hőmérséklet különbség jelentősen meghaladhatja a 10 oC-ot, „hideg” átlagos napi hőmérséklet esetén.
A termikus repedés szempontjából nem feltétlenül kritikus a felterhelt, vagy közvetlenül a terhelés előtti állapot. Adott esetben kedvezőtlenebb lehet a terhelés nélküli, kizárólag a hőmérséklet változásából keletkező lassú tartós termikus feszültség, mert ebben az esetben a húzószilárdság a rendkívül alacsony frekvencia miatt sokkal kisebb 9,0 MPa helyett 3,0-4,0 MPa, de ekkor nem csak a szilárdság, hanem a rugalmassági modulus is csökken, amely (24) miatt csökkentett feszültséget jelent, az arányokat azonban nem ismerjük, mert nem mérjük.
Ezt a viselkedést az AHR aszfalt repedési hőmérséklettel is jellemezhetjük, amit, mint kritikus értéket az út-pályaszerkezet méretezésnél figyelembe lehet venni.
A \( \sigma_{Ttart} \) feszültség okozza az aszfalt „dilatációját”, a felszínen megjelenő tömbrepedést, akár forgalommentes aszfaltfelületeken is. Az aszfaltburkolton megjelenő repedés fokozatos megnyílásának is ez az oka, mivel melegben ez a tartós feszültség se jelentkezik, jelentkezhet, így a megnyílt repedés nem tud záródni, mint a betonok esetén.
Az aszfaltrétegekben keletkező termikus eredetű tartós feszültségek viselkedése egy még nem kellően kutatott, nem megfelelően vizsgált terület, de nem elhanyagolható, mivel a nagyon nagy forgalmú utakon is jelentkezik.
Röviden megemlítem még a bitumen oxidációja miatti öregedés hatásának jelentőségét is, amely folyamat főleg a kopóréteget érinti az aszfaltkeverék hézagtartalmának és a beépítéstől eltelt idő függvényében. A kötőanyag öregedése növeli az aszfaltkeverék rugalmassági modulusát, merevségét. Az öregedés miatti rugalmassági modulus növekedés azért olyan kedvezőtlen, mivel ezt a folyamatot nem követi a húzószilárdság növekedése, vagy legalábbis így gondoljuk, mivel nem mérjük, ezért nem is tudjuk, csak feltételezzük. E miatt a TDC repedések egyik lehetséges okának tekintjük.
Az öregedés elvileg önmagában is okozhat akkora \( \sigma_{Tmax} \) termikus normál feszültséget, hogy törést okozzon a kopóréteg felszínén, de ez egyáltalán nem egy új keletű jelenség, ezt már akkor is tudtuk, amikor a TDC, mint fogalom nem is létezett. Az öregedés hatását a rugalmassági modulus gradiensnél, lehetne és kellene figyelembe venni, de ekkor is szükség van a húzószilárdság és nyomószilárdság értékére, az öregedés függvényében.Az öregedésre vonatkozó egységesen elfogadott modellek és vizsgálati módszerek még nincsenek. Az öregedés azonban nem lehet a TDC repedés kizárólagos ill. fő oka, mivel az öregedésből származó repedéseknek kis forgalmú utakon is jelentkeznie kell. Azonos feltételek mellett gyakoriságuknak hasonlónak kell lennie, mint a nagy forgalmú utakon, de a TDC repedések itt sokkal gyakoriabbak. Az öregedésről csak azt tudjuk állítani, hogy hozzájárul a TDC repedések kialakulásához, de ennek mértéke még nem ismert.
Fáradási élettartam nyírási hányados alapján
A jelenlegi, nem csak a hazai méretezési módszereknél a fáradási élettartam nem egyértelmű, vitatható fogalom. Mást jelent a laboratóriumi vizsgálatok esetén és teljesen más a valós út-pályaszerkezetek tönkremenetele esetén.
A hajlító vizsgálatoknál közmegegyezésen alapul az a felfogás, miszerint a fáradási élettartamot az a teherismétlési szám fejezi ki, amelyik a kezdeti komplex modulus felére csökkenését okozza. Ez a szemlélet különösen fontos az ellenőrzött megnyúlások esetén. Az ellenőrzött feszültség mellett végzett hajlító vizsgálatoknál már akár a tényleges törést okozó teherismétlésig is lehetne folytatni a vizsgálatot, hiszen töréskor már nem tudja a próbatest felvenni a beállított feszültséget, így a töréshez tartozó teherismétlési szám pontosan mérhető. Nagy hátrány, hogy a vizsgálati idő jelentősen megnövekszik, ha az út-pályaszerkezetben keletkező feszültségekhez, mértékadó nyírási hányadoshoz közeli feszültséggel végezzük a vizsgálatot.
A törésig folytatott vizsgálat valós fáradási élettartamot eredményez a hajlító vizsgálat tekintetében, de az út-pályaszerkezetben az egy ponton bekövetkező törés, repedés, még egyáltalán nem jelenti az út-pályaszerkezet tönkremenetelét. Sőt ebben az esetben az útpályaszerkezet megítélése még „kiváló”, látható hibák nincsenek az útburkolat felszínén.
Az út-pályaszerkezetet, akkor tekintjük „tönkrementnek”, ha a burkolat felszínén megjelenő teherbírás csökkenésre utaló repedések az útburkolat felszínének meghatározott 5-10%-át eléri, vagy meghaladja.
A kezdeti repedés megjelenése és a még „elviselhető” repedezettség között eltelt idő alatt lefutott egységtengely áthaladási szám aránya nagyon magas és még nem pontosan ismert. A 17. ábrán a töréshez, repedés megjelenéséhez tartozó egységtengely áthaladási szám 1,44 105 et, vagyis a tönkremenetelhez még ennyi forgalomlefutás szükséges a megfigyelések szerint.
A törésmechanika foglalkozik a repedés terjedési sebességének számításával, Paris-féle modell, amely eredményeket felhasználták a tervező pl. MEPDG programok készítésénél, fejlesztésénél.
Nagyon fontos lenne a hajlító vizsgálatok eredményeként kapott log-log fáradási egyenesek és a valós útpályaszerkezet eddigi megfigyeléseken alapuló a valós tönkremenetelt jellemző log-log fáradási egyenesek közötti pontos összefüggések feltárása.
Ezt a problémát matematikailag egyértelmű összefüggéssel a nyírási hányados segítségével fogom közelítőleg megoldani. A megoldás egzakt lesz, de a megfigyelésen alapuló log-log fáradási görbe (10) nem egzakt, azt még további kutatások során pontosítani kell, amelyre alkalmas tudományterület a törésmechanika.
A nyírási hányados és a hajlító vizsgálatok közül az erővezérelt hajlító vizsgálat kontrollált feszültsége között van közvetlen összefüggés.
A ellenőrzött feszültségek mellett végzett négypontos hajlító vizsgálat eredményeként kapjuk a paramétereket, amelyre felírható a (25).
\[ \sigma_f=c\ N^f; vagy \log{\left(\sigma_f\right)}=\log{\left(c\right)}+\ f\log{\left(N\right)} \]
Az N az a teherismétlési szám, ahol a kezdeti komplex modulus értéke a felére csökken, ha az ellenőrzött húzófeszültség \( \sigma_f \) állandó a teherismétlés során.A négypontos hajlító vizsgálat esetén nem mérjük meg a próbatest hajlító húzószilárdságát \( \sigma_{u,t} \), és nem mérjük a \( \sigma_{u,c} \) nyomószilárdságát se, ezért az \( \alpha \) belső súrlódási szögre, ill. az n értékére vonatkozóan csak becsléssel élhetünk, annak érdekében, hogy a \( \tau_u \) nyírószilárdságot számíthassuk.Korábbi fárasztásos nyomóvizsgálati eredmények [17] alapján igazolható, hogy a nyírási hányados és a teherismétlési szám között is (26) log-log összefüggés van, lásd. 14. ábrát. A T nyírási hányados és az N teherismétlés közötti összefüggés független a vizsgálat hőmérsékletétől, viszont függ az aszfaltkeverék típusától, a belső súrlódási szögtől.A vizsgált aszfaltkeverékek JU20, K20 és AB12/F voltak. A három keverékre kapott nyírási hányadosokat együttesen ábrázolva 14. ábrán is még magas a korreláció.
 |
A hajlító vizsgálatokat nem végezzük törésig, de tudjuk, hogy a törés akkor következik be 15. ábra, amikor az „N” teherismétlés utáni fáradás miatt a \( \sigma_{u,t} \); \( \sigma_{u,c}\ \) lecsökken, és a Coulomb egyenes érinti a vizsgálat során okozott Mohr kört, amelynek sugara a \( \tau_f \) fő-nyírófeszültség. A fáradás során feltételezzük, hogy az aszfaltkeverék belső súrlódási szöge nem változik. A teljes tönkremenetel, amikor az aszfaltkeverékben a zúzalékok között a kötőanyag már nem biztosítja a kohéziót. Ez egy elméleti végső határ, amit az aszfaltkeverék csak megközelíthet, de sose éri el, ebben az esetben a zúzalékok között csak súrlódás van. Hasonló meghibásodási kritériumot alkalmaztak a betonban keletkező repedések kialakulási és terjedési modellezésénél [15, 16].
 |
A négypontos hajlítás vizsgálatkor a húzott oldalon egyirányú normál húzófeszültség alakul ki, míg a másik két főtengely irányú normál feszültség nulla, ezért a (3) így irható fel:
\[ \tau_u=\frac{\sigma_{u,t}+\left(\sigma_{u,t}-\sigma_f-0\right)\sin{\alpha}}{2}=\frac{\sigma_f(k+\left(k-1\right)\sin{\alpha)}}{2}\ \]
ahol:
\( k=\frac{\sigma_{u,t}}{\sigma_f} \)
A hajlító vizsgálatoknál a \( \sigma_{u,t} \) húzószilárdságot nem mérjük, de vizsgálatokkal megalapozottan meghatározhatunk egy olyan 1-10 terjedő \( N_{t} \) törési teherismétlési számot, amely a (25) vizsgálati eredménybe helyettesítve megadja a \( \sigma_{u,t} \) keresett húzószilárdságot:
\[ \sigma_{u,t}=c\ {N_t}^f \]
A másik lehetőség az ITS vizsgálatból számítani a tiszta húzáshoz tartozó \( \sigma_{u,t} \) húzószilárdságot.A négypontos erővezérelt vizsgálati eljárással meghatározott fáradási élettartamhoz tartozó N teherismétlési szám nem csak az ellenőrzött feszültséggel (23), hanem a nyírási hányadossal is kifejezhető.
\[ \log{\left(N\right)}=a\ log(T)+b \]
A négypontos erővezérelt hajlító vizsgálatnál a (26) és (29) segítségével a (30) nyírási hányados:
\[ \tau_f=\ \frac{\sigma_f}{2} \]
\[ T=\frac{\tau_f}{\tau_u}=\frac{\sigma_f}{\sigma_{u,t}+\left(\sigma_{u,t}-\sigma_f\right)\sin{\alpha}} \]
Az a és b paraméterek számításához a (23) vizsgálati eredményt az \( N={10}^6 \) és \( N=10^{5} \) teherismétlésre illesztjük, amelynek levezetése az a és b paraméterekre:
\( N= 10^{6} \) esetén:
\( \log{\left(N\right)}=a\ log\left(T\right)+b , és N=\ {10}^6 , akkor 6=a\ log\left(T\right)+b \)
\( k_6=\frac{\sigma_{u,t}}{\sigma_{f6}} \)
\( =a\ log\left(\frac{1}{k_6+\left(k_6-1\right)\sin{\alpha)}}\right)+b;\)
\( a=\frac{6-b}{log\left(1\right)-log(k_6+\left(k_6-1\right)\sin{\alpha)}}=\frac{6-b}{-\log(\frac{\sigma_{u,t}}{\sigma_{f6}})+\left(\frac{\sigma_{u,t}}{\sigma_{f6}}-1\right)\sin{\alpha}} \)
\( N=10^{5} \) esetén:
\( \log{\left(\sigma_5\right)}=\log{\left(c\right)}+\ f\log{\left({10}^5\right)} \); \( \sigma_5={10}^{\log{\left(c\right)}+5\ f} \)
\( k_5=\frac{\sigma_{u,t}}{\sigma_{f5}}\tau_{u,5}=\frac{k_5\sigma_{f5}+\left(k_5\sigma_{f5}-\sigma_{f5}-0\right)\sin{\alpha}}{2}=\frac{k_5\sigma_{f5}+\left(k_5\sigma_{f5}-\sigma_{f5}\right)\sin{\alpha}}{2} \)
\( \tau_5=\ \frac{\sigma_{f5}}{2}T_5=\frac{\tau_5}{\tau_{u,5}}=\frac{\sigma_{f5}}{k_5\sigma_{f5}+\left(k_5\sigma_{f5}-\sigma_{f5}\right)\sin{\alpha}} \)
\( 5=a\ log\left(\frac{\sigma_{f5}}{k_5\sigma_{f5}+\left(k_5-\sigma_{f5}\right)\sin{\alpha}}\right)+b \); \( a=\frac{5-b}{log\left(\sigma_{f5}\right)-\log\left[k_5\sigma_{f5}+\left(k_5\sigma_{f5}-\sigma_{f5}\right)\sin{\alpha}\right]} \)
\( \frac{5-b}{log\left(\sigma_{f5}\right)-log{\left[k_5\sigma_{f5}+\left(k_5\sigma_{f5}-\sigma_{f5}\right)\sin{\alpha})\right]}}=\frac{6-b}{-log{({\frac{\sigma_{u,t}}{\sigma_{f6}}}}+\left(\frac{\sigma_{u,t}}{\sigma_{f6}}-1\right)\sin{\alpha}} \)
\( log\left(\sigma_{f5}\right)-\log{\left[\sigma_{u,t}+\left(\sigma_{u,t}-\sigma_{f5}\right)\sin{\alpha}\right]}=X \)
\( -\log(\frac{\sigma_{u,t}}{\sigma_{f6}})+\left(\frac{\sigma_{u,t}}{\sigma_{f6}}-1\right)\sin{\alpha}=Y \)
\[ b=\frac{5Y-6X}{Y-X}; és a=\frac{6-b}{Y} \]
A nyírási hányadossal és az a és b paraméterekkel a (28) egyenlet alapján számított N teherismétlés és a (25) alapján számított teherismétlés azonos, ahol a \( \tau_u \) fő-nyírófeszültség és az ellenőrzött \( \sigma_f \) húzófeszültség között fennáll a (26).
A nyírási hányados T úgy határozható meg a mért \( \sigma_f \) húzófeszültségből, hogy a (25)-ból \( \sigma_{f} \); c;f segítségével számítjuk az N teherismétlést, majd a (28) alapján a (25)-ből kapott N teherismétlési szám, valamint az a;b paraméterekkel számítjuk a T nyírási hányadost.
Az így kapott T és σf értékpárok a (25) és a (28) összefüggéseknél azonos N teherismétlési számot eredményeznek, ha n=1, amikor \( T=\frac{\sigma_f}{\sigma_{u,t}} \) speciális eset áll fenn, mert \( \sin{\alpha=0} \).
Logikusnak tűnik, hogy a nyírási hányadost így határozzuk meg, hiszen a hajlítási vizsgálatot \( 0-\sigma_f \), míg a tiszta húzáshoz tartozó törés is ezen a vonalon történik \( 0-\sigma_{u,t} \). A tiszta húzáshoz tartozó \( \sigma_{u,t} \) húzószilárdság kitüntetett szerepe azonban nem indokolható. Kitüntetett szerepe a \( \sigma_{u,c} \) tiszta nyomásnak, vagy akár a tiszta nyírásnak, ill. csavarásnak is lehetne.
A (30) szerinti nyírási hányados számítási módszerét indokolja, hogy a törést okozó nyírófeszültséghez szükséges belső energia a Coulomb egyenessel arányosan növekszik a tiszta nyomás állapotáig.
Az n=2 a belső súrlódási szög figyelembevétele az illesztési pontok N=105 és N=106 kivételével nem teszik lehetővé a tökéletes megfelelést, de az eltérés elhanyagolható, amit egy példán keresztül mutatok be.
A 2. táblázatban szereplő „A” minta \( \sigma_f;c;f \) (25) alapján az \( N = 10_{7} \) teherismétlés esetén a \( \sigma_f \) = 0,934 MPa, és a (30) szerint számított nyírási hányados T=0,053775. Az így kapott nyírási hányadossal az a;b paraméterekkel számított (26) teherismétlési szám N=9,77 \( 10^{6} \).
Az eltérés oka a 15. ábra szerinti 1 teherismétléshez tartozó nyírószilárdság \( \tau_{u,t} \) és az N teherismétléshez tartozó \( \tau_u \) nyírószilárdság közötti eltérés, amit a vizsgálati c; f paraméterek megadásánál nem veszünk figyelembe.A nyírási hányados (30) nagyobb valószínűséggel független a hőmérséklettől és ennek következtében a terhelés frekvenciájától is, mintha függőséget tételeznénk fel.
Ezt támasztja alá a 14. ábrán feltárt összefüggés is, ezért az erővezérelt hajlító vizsgálat alapján meghatározott nyírási hányados és a „terepi” út-pályaszerkezetben keletkező nyírási hányados hatása nem változhat. Ha a laborvizsgálat során T nyírási hányados N teherismétlés után törést, repedést okoz, akkor a „terepen” a valós út-pályaszerkezetben a terhelés körülményeitől, típusától stb. függetlenül, az adott terhelésből számított T nyírási hányados N teherismétlés után is törést, repedést fog okozni.A „terepi” út-pályaszerkezetet egy mértékadó aszfaltkeverékkel jellemezzük, amelyre a mértékadó törékenységet \( R_m \) állandót kell meghatározni.
A „terepi” út-pályaszerkezet fáradási görbéjére (9) fogadjuk el, amit a helyettesíthetünk (11)-el, ha ismerjük a mértékadó \( R_m \) törékenységet.
Ha a még nem ismert, de meghatározandó \( R_m \) törékenységű mértékadó aszfaltkeveréken négypontos erővezérelt hajlító vizsgálatot végzünk adott hőmérsékleten és frekvencián, akkor a mérési eredményül kapott c;f paraméterekkel, valamint a (12) fáradási görbe segítségével meghatározható egy átviteli függvény.Az átviteli függvény segítségével bármely aszfaltkerékre vonatkozóan számítható a hajlító-vizsgálattal mért \( N_{rep} \) teherismétlés és T nyírási hányados alapján a „terepi”, beépített aszfaltkeverék valós tönkremeneteléhez tartozó \( {TF}_m \) várható egységtengely áthaladás.
Az \( N_{rep} \) teherismétlés, egységtengely áthaladás után a vizsgált út-pályaszerkezeti rétegben megjelenik a repedés, és a \( {TF}_m \) várható egységtengely áthaladás után az útburkolat felületén megjelenő repedések aránya meghaladja, eléri a megengedett 5-10%-ot.
Az erővezérelt négypontos hajlító vizsgálat hazánkban nem előírás, így nem szoktuk elvégezni. A mintapélda kedvéért kerestem egy jól dokumentált tudományosan megalapozott és elfogadott anyagot, ahol ilyen vizsgálatot végeztek. Ezt Almássy Kornél Ph.D. értekezésében [16] találtam meg, ahol a vizsgálati hőmérséklet 10 oC, a frekvencia10 Hz volt.
A vizsgálati eredményekből 6 mintát választottam, annak bemutatására, hogy a nyírási hányados alapján levezetett elmélet valós eredményeket szolgáltat annak ellenére is, hogy a vizsgálati hőmérséklet eltér az út-pályaszerkezetben keletkező mértékadó feszültségek számításánál felvett 20 oC-tól és a 4000 MPa rugalmassági modulustól.
Amikor a 10 Hz frekvencián és 10 oC-on végzett négypontos erővezérelt hajlító vizsgálat eredményeit használjuk fel, akkor azt is feltételezzük, hogy a vizsgálat eredményéül kapott \( \sigma_f \); c;f paraméterekből számított a;b paraméterek pl. a 10 Hz frekvencián és 20 oC-on vizsgáltat esetén eredményül kapott \( \sigma_f^\prime \);\( c^\prime;\ f^\prime \) paraméterekből is a;b paramétereket kapnánk eredményül, mivel a nyírási hányados független a hőmérséklettől és a terhelés frekvenciájától, legalábbis a mért [17] hőmérséklet tartományban.
A vizsgálatok [18] eredményéül kapott c;f paramétereket és a (29) számított a;b paramétereket a 3. táblázat tartalmazza. A nyírási hányados azonban függ 15. ábra a tiszta húzásból származó húzószilárdságtól \( \sigma_{u,t} \) és a tiszta nyomásból származó \( \sigma_{u,c} \) nyomószilárdságtól, amiket általában nem mérünk. A \( \sigma_{u,t} \) húzószilárdság a (27) N=1 esetén számítható, amely esetben \( \sigma_{u,t}=c \). Ez a megközelítés azonban adott esetben teljesen irreális eredményt ad, ami abból ered, hogy a c;f illesztési paraméterek meghatározásánál figyelmen kívül hagyjuk a minta húzószilárdságát, mert nem mérjük.
| sf (Mpa) N=106 | Minta | c | f | b | a |
| 1,364 | A | 13,257 | -0,165 | -0,481 | -5,885 |
| 1,364 | B | 20,917 | -0,198 | -0,460 | -4,956 |
| 1,463 | C | 6,182 | -0,104 | -0,479 | -8,946 |
| 1,487 | D | 9,261 | -0,132 | -0,490 | -7,198 |
| 1,341 | E | 7,978 | -0,129 | -0,489 | -7,367 |
| 1,893 | B’ | 8,128 | -0,11 | -0,483 | -8,525 |
Megtehetjük, hogy a húzószilárdságot másfajta vizsgálattal pl. dinamikus hasító vizsgálattal (16) határozzuk meg. A \( \sigma_{u,t} \) húzószilárdság függ a mérési hőmérséklettől és a mérési frekvenciától is, ezért az eltérő vizsgálati módszerekkel kapott eredményeket a vizsgálati hőmérséklet és frekvencia alapján át kell számítani. Az átszámításhoz segítségünkre lehet az aszfaltkeverékre előállított mestergörbe is, ha mérjük.A „B” minta húzószilárdsága a c=20,911 és f=-0,198,N=1 paramétereknél 20,92 MPa. A (B’)-nél a 20,92 MPa húzószilárdságot, önkényesen 8,0 MPa-ra módosítottam, ebben az esetben a 16. ábra szerint a B mintához tartozó c;f illesztési paraméterek jelentősen változtak, de még mindig magas korreláció mellett.
 |
Az A-E mintákra a (11) szerint av=-0,4756 és bv=2,4539 számítottam a \( {TF}_m \) mértékadó tervezési forgalmakat 17. ábra, ahol n=2; \( {R_m=E/\sigma}_{u,t}=1000 \). Tervezésnél a mértékadó hőmérséklet 20 oC, amelyhez tartozó rugalmassági modulus E=4000 MPa. A vízérzékenységhez mért ITS hasító-húzó szilárdság mértékadó értékét 1,6 MPa-ra vettem fel, (15)-ből a \( \sigma_{u,t} \) húzószilárdság 4,0 MPa., \( R_m=\frac{E}{\sigma_{u,t}}=1000 \).
 |
Ha a hajlítóvizsgálat során \( N_{rep} \) teherismétlés után és T nyírási hányados esetén a próbatest eltörik, vagy az egységes tönkremeneteli értelmezés szerint a komplex modulusa felére csökken, akkor a beépített pályaszerkezetben is \( N_{rep} \) teherismétlés, egységtengely áthaladás és T nyírási hányados mellett repedés, folyás keletkezik a tönkremenetel vizsgálati értelmezésétől függően.A valós pályaszerkezet egy pontjának tönkremenetele azonban nem jelenti még a teljes pályaszerkezet tönkremenetelét. A következőkben egy mintapéldán keresztül, bemutatom az \( N_{rep} \)-hez tartozó egységtengely áthaladási szám és az UME-ban alkalmazott (10) fáradási görbe \( {TF}_m \) egységtengely áthaladási szám közötti összefüggést biztosító átviteli függvény számításának elvét.
Az UME-ban alkalmazott (11) fáradási görbe nem egy mechanikai alapon meghatározott pontos összefüggés, de nagy előnye, hogy viszonylag jól jellemzi a magyarországi körülményeket és több évtizedes múltra tekint vissza.
A nyírási hányados segítségével lehetőség nyílik a (11) mechanikai alapú pontosítására, és az időközben megváltozott aszfaltkeverékek mechanikai tulajdonságainak figyelembevételére is.
Új út-pályaszerkezeteknél a beépített aszfaltkeverékek fáradása érdekel minket, de az út-pályaszerkezet megerősítésnél is elsősorban az új, a megerősítő aszfaltréteg fáradási tulajdonsága a fontos számunkra.
A mértékadó aszfaltkeveréket mértékadó törékenységét \( R_m=1000 \) paraméterrel határoztam meg.
 |
A terepi és a laboratóriumi körülmények közötti nagyon jelentős különbségeket egy nagyon egyszerű, de fizikai jelentésében egy igen komplex és összetett átviteli függvénnyel tudjuk biztosítani. A továbbiakban egy ilyen átviteli függvény számítási lehetőségét ismertetem.
Az átviteli függvény meghatározásához a mértékadó aszfaltkerék ismerete szükséges, amely lehet több aszfaltkerékből mért, adott valószínűségi változóhoz tartozó aszfaltkeverékek R törékenysége és a négypontos hajlító vizsgálat log-log összefüggése.
A mintapéldában a mértékadó aszfaltkeveréknek a 4. táblázatban szereplő B’ mintát jelöltem ki, ahol feltételezzük, hogy a log-log egyenes határolja az elvárt valószínűségi tartományt.
A törékenységet a példa kedvérét \( R_m=2000 \)-re vettem fel – amihez szintén tartozik egy megadott valószínűségi küszöbszint -, ezért az UME-ban meghatározott (9) fáradási görbéhez a 2. táblázat szerint R=2000 esetén av= -0,3583; bv=2,5106.
A 18. ábrán együtt szerepelnek a „terep” (11), amellyel az UME (10) fáradási görbéjével nagyon magas regresszióban van és az erővezérelt négypontos hajlító-vizsgálattal megadott „labor” B’ minta log-log fáradási görbéi.
A terepi/labor görbe hányadosa adja azt az átviteli függvényt (32), amelynek h;j paramétereivel (33) meghatározható a (34) fáradási görbe.
Átviteli függvény:
\[ \log(T)=h\log{\left({TF}_m\right)}+j \]
\[ h=av-\frac{1}{a_m}; és j=bv+\frac{b_m}{a_m} \]
Fáradási görbe:
\[ \log{\left({TF}_m\right)}=\left(h+\frac{1}{a}\right)\log{\left(T\right)}+j-\frac{b}{a} \]
ahol:
a és b – az erővezérelt négypontos hajlító vizsgálat (28) szerinti paraméterei
h és j – az átviteli függvény paraméterei.
\( a_m \) és bm – a mértékadó aszfaltkeverékből készült próbatesten végzett erővezérelt négypontos hajlító vizsgálat (28) szerinti paraméterei.
Mivel B’ minta a példában a mértékadó aszfaltkeverék is, ezért \( a_{m}=a \) és bm=b, amelynek eredményeként a (34) –ből számított \( {TF}_m \) tervezési forgalom egyezni fog a (12)-ből számított tervezési forgalommal azonos T nyírási hányados mellett n=1 esetén. Az n>1 esetén az a (30) a;b paraméterek a vizsgálati c;f paraméterekre illesztés miatti a számított tervezési forgalmak között elfogadható eltérés lesz.
Ha a mértékadó aszfaltkeveréktől eltérő aszfaltkeveréket vizsgálunk, akkor az erővezérelt négypontos hajlító-vizsgálat alapján kapott a, b paraméterekkel a beépített aszfaltkeverékre vonatkozó várható fáradási görbe (34) szerint számítható, ahol T nyírási hányados a beépített útpályaszerkezetben keletkező nyírási hányados.
A nyírási hányados alapján történő út-pályaszerkezet méretezése a (32) átviteli függvény ismerete nélkül is alkalmazható, de ebben az esetben – a jelenlegi tervezési gyakorlattal egyezően – közvetlenül nem tudjuk figyelembe venni a beépített aszfaltkeverékek eltérő fáradási élettartamát, de a \( \sigma_{u,t} \) húzószilárdság fáradási élettartamra gyakorolt hatása ekkor is számítható, amely nem más mint az aszfaltkeverék R törékenységének hatása.
Azt azonban tudjuk, hogy a fáradási élettartamot nem csak a húzószilárdság befolyásolja.A nyírási hányados alkalmazását a mértékadó aszfaltkeverék pontos ismerete nélkül egy példán keresztül mutatom be. Ebben az esetben R_m=1000 felvételét javaslom, amelyre 2. táblázat szerint av= -0,4756; bv=2,4539.
Az \( R_m \) mértékadó törékenység határozza meg a (11) fáradási görbe av, bv paramétereit.A tervezett út-pályaszerkezet felépítése R=1000 törékenység mellett a ragasztás hatásának figyelembe vétele nélküli ideális esetben:
18,0 cm AC(3)
20 cm M63 mechanikai stabilizáció
altalaj 69 MPa
AC(3) rugalmassági modulusa E=4000 MPa, húzószilárdsága \( \sigma_{u,t}=4,0 \) MPa; így R=1000.50 kN terheléssel 150 mm átmérőjű tárcsával az FWD behajlás a tárcsa tengelyében, \( S_{din}=0,588 \) mm.
A statikus behajlás (11) szerint, \( S_m=1,105{\ S}_{din} \) ;\( S_m=0,65 \) mm.
A tervezési forgalom (10) szerint \( {TF}_m \) = 1,37 106.
A tervezett út-pályaszerkezetben keletkező nyírási hányados T=0,32 az aszfaltréteg alján 18 cm mélységben, a (12) szerint számított tervezési forgalom \( {TF}_m \) = 1,58 106.
A legnagyobb behajlás alapján történő méretezéssel kapott \( {TF}_m \) = 1,37 106 , alig tér el az aszfaltréteg alatt kapott T=0,32 nyírási hányadosból számított \( {TF}_m \) = 1,58 106 –től, a két méretezés az aszfalt pályaszerkezet alsó síkja tekintetében közel egyenértékű (12) miatt.
Ha azonban a 18 cm vastagságú aszfaltkeverék húzószilárdsága a \( \sigma_{u,t}=4,0\) MPa helyett csak \( \sigma_{u,t}=2,0\) MPa, akkor a törékenység R=2000-re növekszik.
A legnagyobb behajlás szerinti méretezés nem változik, mivel a rugalmassági modulusok se változtak, így a tervezési forgalom (10) szerint \( {TF}_m \) = 1,37 \( 10_{6} \) egységtengely áthaladás is változatlan marad, sőt a legnagyobb fajlagos megnyúlás is változatlan marad.
Az út-pályaszerkezeti rétegekben a keletkező feszültségeket a rugalmassági modulusok határozzák meg, ha a rugalmassági modulusok nem változnak, akkor az út-pályaszerkezetben keletkező feszültségek és fajlagos megnyúlások is változatlanok maradnak.Az út-pályaszerkezeti rétegek szilárdságának változása változatlan rugalmassági modulus mellett az út-pályaszerkezeti rétegek fáradásának változását okozza/eredményezi. Ezt a változást a legnagyobb behajlás alapján, és a fajlagos megnyúlások alapján se tudjuk kimutatni, ez csak és kizárólag a nyírási hányados alapján lehetséges.
A minta példában a húzószilárdság \( \sigma_{u,t}=4,0 \) MPa –ról \( \sigma_{u,t}=2,0\ \) MPa-ra csökkenése miatt az út-pályaszerkezetben keletkező nyírási hányados az aszfaltréteg alján 18 cm mélységben T=0,707-ra növekszik, így a (14) szerint számított tervezési forgalom \( {TF}_m \)= 0,3 \( 10_{6} \)-ra csökken. A fáradási élettartam csökkenésének oka az R törékenység értékének megduplázódása.
Az R törékenységet a jelenleg az aszfaltkeverékekre előírt vizsgálatokkal is meg lehetne határozni és elvileg ki lehetne szűrni a fáradási élettartam szempontjából kedvezőtlen aszfaltkeverékeket.Intenzív igénybevételi kategória esetén elő van írva az MSZ EN 12 697-24 fáradási vizsgálat, amely közvetve alkalmas a nagyon magas R törékenységű aszfaltkeverékek kiszűrésére, mivel a magas R törékenység szükségképpen alacsony fáradási élettartamot okoz, de nem alkalmas a törékenység számítására, mivel a vizsgálóberendezések szoftvere nem engedélyezi az N=1 teherismétlés esetén a próbatest eltörését.
Az R törékenység a dinamikus hasító-húzó vizsgálatból IT-CY [19] is számítható lenne, ha a készülék és a vizsgálati szabvány lehetőséget biztosítana a \( \sigma_{H,h} \) hasító-húzó szilárdság mérésére. A vizsgálati minta eltöréséhez általában nem elegendő a készülékek által biztosított maximális terhelő erő.
Jelenleg a \( \sigma_{H,h} \) hasító-húzó szilárdságot vizsgálatát külön szabvány írja elő, ahol a vizsgálat az IT-CY-től eltérő készülékkel, eltérő terhelési móddal és sebességgel készül. Az UME a vízérzékenység vizsgálatnál az ITS hasító-húzó szilárdság vizsgálatát az IT-CY-től eltérő hőmérsékleten és eltérő tömörítési móddal írja elő.
Az R törékenység meghatározásához miden szükséges vizsgálatot elvégzünk, de a jelentősen eltérő vizsgálati körülmények miatt a törékenység és a húzószilárdság jelenleg csak becsülhető.
A nagyteherbírású út-pályaszerkezetekben alkalmazott aszfaltkeverékeket szükségképpen úgy tervezzük, hogy ellenállók legyenek a deformációval szemben. E miatt eleve merevebbek, nagyobb rugalmassági modulusúak. A húzószilárdságra viszont nincsenek előírások az R törékenység nem ellenőrzött, a kopórétegre még fáradási előírás sincs.
„K” forgalmi terhelési osztály felett a kopóréteg tönkremenetele lesz a kritikus a nyírási hányados alapján. A „C1” típusú 24 cm aszfaltréteg vastagságú út-pályaszerkezetnél a kopóréteg alatt keletkező nyírási hányados T=0,161 lesz, \( {TF}_m \) = 6,7 \( 10_{6} \) egységtengely áthaladás, míg az aszfaltréteg alatt T=0,086 lesz, \( {TF}_m \) = 25,3 \( 10_{6} \) .
Ha erre a szerkezetre még ráteszünk 4 cm kopóréteget, akkor az új kopóréteg alatt a változatlanul T=0,161 marad, \( {TF}_m \) = 6,7 \( 10_{6} \) egységtengely áthaladás, míg az aszfaltréteg alatt T=0,079 lesz, \( {TF}_m \)= 29,9 \( 10_{6} \)-re növekszik.
„K” forgalmi terhelési osztály felett a „C1” típusú út-pályaszerkezetet hiába erősítjük, vastagítjuk a kritikus nyírási hányados nem változik, az út-pályaszerkezet megerősítése már nem vezet elfogadható eredményre.
A megoldás a kopó és a kötőréteg R törékenységének csökkentése az aszfaltkeverék szilárdságának növelésén keresztül. Kerülni kell a rugalmassági modulus csökkentését, mivel egyrészt ennek következményeként a pályaszerkezetben keletkező feszültségek növekednek, ha a rugalmassági modulust csökkentjük, másrészt a deformációval szembeni ellenállás is csökken. Az aszfaltkeverékek fárasztási vizsgálata segít abban, hogy a különböző teljesítményű aszfaltkeverékek közül ki tudjuk választani a legmegfelelőbbet [20].
A másik lehetőleg párhuzamos megoldás a ragasztóanyag nyírási modulusának jelentős növelése, akár a modifikálószer arányának emelése árán is.Ezen kívül javítani kell a kötőanyag és a kőváz közötti tapadást a megfelelő anyagok felhasználásával, esetleg tisztításával.
A „K” forgalmi terhelési osztálytól alacsony R törékenységű és magas rugalmassági modulusú aszfaltkeverékekre van szükség, ami szükségessé teszi az aszfaltkeverék tervezésének újragondolását is.
Összefoglalás
A bemutatott töréselmélet szerinti mértezéssel számítani tudjuk az azonos rugalmassági modulusú, de eltérő szilárdságú aszfaltkeverékek fáradási élettartamának különbségét is. A legnagyobb behajláson, vagy a megengedett megnyúláson alapuló méretezési módszereknél ez nem lehetséges. Az aszfaltkeverék szilárdságának felére csökkenése, akár a tervezett élettartam negyedére csökkenését is okozhatja, amely jelentős nemzetgazdasági veszteséggel járhat.
A levezetett töréselmélettel bizonyítottam, hogy a legnagyobb behajlás szerinti méretezésnél jelenleg alkalmazott fáradási görbe, egy állandó értékű \( R_m \) mértékadó törékenységet reprezentál.
Az elkövetkező évek fontos vizsgálati területe kell legyen a magyarországi közúthálózatba már beépített aszfaltkeverékek \( R_m \) mértékadó törékenységének meghatározása, pontosítása évszakonként, vagy havonkénti bontásban. Az \( R_m \) mértékadó törékenységének fontos szerepe lesz a most nem tárgyalt repedésterjedés modellezésénél.
A töréselméleten alapuló módszer nagy előnye, hogy \( R_m\ \approx1000 \) arányszám mellett, a törékenység pontos ismerete nélkül is alkalmas a legnagyobb behajlás szerinti méretezési módszer azonnali kiváltására. A módszerváltást az aszfaltkeverékek szilárdsági, hasító-húzószilárdsági jelentős ingadozása teszi szükségessé, mivel csak a töréselmélet szerint lehet a szilárdság változásából származó élettartam változást számolni, megbízhatóan becsülni.
A hasító-húzó szilárdság és a merevség vizsgálatát az IT-CY [17] szerint kell elvégezni, ahol nemzeti szinten szabályoznunk kell a hasító-húzószilárdság mérését, ennek alapján egy vizsgálaton belül megbízhatóan meghatározható a vizsgált aszfaltkeverékre vonatkozó R törékenység.
Az R törékenység alapján szabályozható a fáradás szempontjából megfelelő aszfaltkeverékek köre, ami egy viszonylag olcsó és könnyen ellenőrizhető paraméter, és jól kiegészíti az aszfaltkeverékekre jelenleg előírt fáradási vizsgálatot.
Az út-pályaszerkezet méretezésnél nem hagyható figyelmen kívül az út-pályaszerkezeti rétegek együttdolgozását biztosító ragasztóréteg, nyírási modulusa, vastagsága a megfelelő rétegtapadáson túlmenően.A ragasztóréteget, mint önálló pályaszerkezeti réteget kell figyelembe venni, ehhez azonban olyan programok kellenek, amelyek ilyen számításokat is képesek kezelni, megoldani.
Nem megkerülhető, hogy hazai fejlesztésű programra is szükségünk van a kiszolgáltatottság megszüntetése érdekében.
A töréselméleten alapuló módszerrel bizonyítottam, hogy a nagyon nagy forgalmi terhelésű utakon a nem megfelelő törékenységű és hasító-húzószilárdságú kopóréteg a tervezési időszak előtt, akár a szavatossági időn belül is tönkre mehetnek, amit csak súlyosbíthat a nem megfelelő ragasztóanyag alkalmazása, előírása.
Irodalomjegyzék
[1]: National Academies of Sciences, Engineering, and Medicine. 2018: A Mechanistic Empirical Model for Top Down Cracking of Asphalt Pavements Layers. Washington, DC: The National Academies Press. https://doi.org/10.17226/25304.
[2]: E. Freitas & P. Pereira, L. Picado-Santos 2016: Assessment of Top-Down Cracking Causes in Asphalt Pavements
[3]: F. Canestrari & L. P. Ingrassia 2020: A review of top-down cracking in asphalt pavements: Causes, models, experimental tools and future challenges. Jurnal of Traffic and Transportation Engineering 2020; 7 (5): 541-572, https://doi.org/10.1016/j.jtte.2020.08.002
[4]: Király, T. & Primusz, P. 2020: A gumiabroncs és az útpályaszerkezet érintkezési kapcsolatának elemzése végeselem módszerrel, Útügyi lapok, 8. évfolyam, 14. szám. https://doi.org/10.36246/UL.2020.2.04
[5]: Aszfaltburkolatú Útpályaszrekezetek Alternatív Méretezési Módszere. 2016: Tervezési Útmutató
[6]: Austroads: Guide to Pavement Technology Part 2. 2017: Pavement Structural Design. Sydney
[7]: e-UT 06.03.13:2005 UME, Aszfaltburkolatú útpályaszerkezetek méretezése és megerősítése.
[8]: Zsichla, L. 2023: Évszaki szorzók, talajteherbírási modulus számítása a mért behajlási teknők segítségével, billenőkaros behajlásmérés bizonytalansága; Útügyi lapok, 11. évfolyam, 17. szám. https://doi.org/10.36246/UL.2023.1.06
[9]: MSZ EN 12697-23: Aszfaltkeverékek. Vizsgálati módszerek, 23. rész: Aszfalt próbatestek hasító-húzó szilárdságának meghatározása.
[10]: Török, K. 2000: Az aszfaltkeverékek mechanikai, és fizikai tulajdonságainak laboratóriumi vizsgálatai. BME Útlabor.
[11]: Török, K., Pallós, I. & Nemesdy, E. 1985: Az aszfaltmechanikai vizsgálatok kifejlesztése a BME Útépítési Tanszékén. 122-128 oldal
[12]: Skronka, G., Tóth J. 2022: A bitumen keverőgépi viszkozitásának mérése és a módszer lehetséges szerepe egy bitumen átvételi rendszer részeként. Az Aszfalt XXIX. éfv. 2022/2. szám
[13]: Rosta, Sz. & Zvekán, F. 2021: Visszanyert aszfaltok bitumenjének reológiai vizsgálatának lehetősége, szükségessége. Az Aszfalt XXVIII. évf. 2021/2. szám
[14]: Török, K. & Pallós, I. 2015: Az aszfaltok téli hidegviselkedését befolyásoló anyagtulajdonságok laboratóriumi vizsgálatai. Útügyi Lapok 3 évf. 5. szám.
[15]: Carol, I., Bazant, Zp. & Prat, P.C. 1992: Microplane type constutive models for distrubuted demage and localized cracing in concrete structures, Proc. Fracture Mechanics of Concrete Structures, Elsevier, Breckenridge, CO, pp. 299-304.
[16]: Saouma, V. 2000: Fracture mechanics, Univercity of Colorado, Boulder, CO 80309-0428
[17]: Zsichla, L. 1997: Aszfaltok komplex fáradási élettartamának meghatározása egyszerűsített módszerrel. Fővárosi Főpolgármesteri hivatal
[18]: Almássy, K. 2010: Aszfalt pályaszerkezeti rácsok viselkedése. Ph.D. értekezés
[19]: MSZ EN 12697-26: Aszfaltkeverékek. Meleg aszfaltkeverék vizsgálati módszerei, 26. rész: Merevség
[20]: Zsichla, L. 2023: Különböző aszfaltkeverékek teljesítményének összehasonlítása, mechanikai alapú értékelési módszertana többrétegű út-pályaszerkezet esetén. Az Aszfalt 2023/1. szám 31-40. oldal
[21]: Schleeh, W. 1978: Zur Ermittlung der Spaltzugfestigkeit des Betons. In: Beton (1978), Nr. 2, S. 57–62
[22]: Lenz Peter, 2012: Beton-beton-verbund potenziale für schubfugen. Dissertation, Technischen Universität München.
Erre a szövegre így hivatkozhat:
Zsichla László: Út-pályaszerkezet méretezése törés-elmélet alapján, 2023, DOI: 10.36246/UL.2023.2.07
