https://doi.org/10.36246/UL.2023.2.06
2023; 11. évfolyam, 18. szám
Bevezető, Előzmények
A világ egyik legrégebbi és legismertebb terepi mérési módszere a „Load-Plate Test” statikus tárcsás teherbírás mérés. Az első részben a nemzetközi és hazai szabványok tanulmányozásakor felismertük, hogy a terhelés sebessége, kivárások, ezek hatása az eredményre döntőek. A mérési eredmények jelentősen eltérőek lehetnek. Jelen részben a teherbírásmérés alakváltozásából számítható és a tömörséget jellemző paraméterek bemutatásával, kritikájával és más lehetséges javaslatokkal foglalkozunk.
Az eső részben [12] arra jutottunk, hogy a statikus tárcsás mérés innovációjával, a mérési módszer módosításával a jelenleginél jobb ismételhető teherbírási eredményeket lehessen elérni. A statikus tárcsás teherbírás mérésekor a lépcsőzetes terhelés hatására a szemcsés réteg / talaj tulajdonsága (tömörsége, teherbírása) is változik, azaz kölcsönhatásban vannak.
A különböző szabványok – hasonlóságuk ellenére – igen sok eltérést rejtenek, de a megvalósíthatóságban a humán faktor bizonyult a legnagyobb hibalehetőségnek. Ugyanazt a mérést mindenki egy kicsit másképp végzi el, sőt ugyanazt az eredményt ugyanaz a mérőszemélyzet sem tudja megismételni – legjobb szándéka mellett sem. A mérési munkakörülmények rendkívül rosszak, fárasztóak. A nehéz tárcsák elhelyezése, a felállás a méréshez kimerítő feladat. Ki kellett jelentsük, hogy a mérés automatizálása az egyetlen hatékony megoldás. Az amerikai, brit és német szabványokból hasonló következtetésre juthattunk. Lehetetlen a párhuzamos mérés bevezetése, mert a vizsgálat ismételhetősége gyenge. Ez azért is mellbevágó, mert a teherbírás mérés egy fontos minősítő vizsgálatunk.
Áttekintettük az első részben a mérési eszközök kialakításait, milyen előnyöket és hátrányokat mutatnak, miben térnek el. A mérések előkészítése, a műszer felállításának feladata nehéz és sok időt vesz igénybe a terepen, egyszerűsítése indokolt. Később ezeknek a tapasztalatoknak nagy szerepe lehet a mérés innovatív továbbfejlesztéséhez, egy automata műszer kialakításával [11]. Elleneztük továbbá a Boussinesq képletben szereplő (1-μ2)∙c szorzat „egyszerűsítését”, a Poisson tényező elhanyagolását. Vizsgáltuk az egy mérőóra, vagy három kérdését, a merevítő bordák szükségességét, a hatásmélységet. Elvégeztük a magyar tárcsás vizsgálat hibáinak feltárását. Az ismertetett részletes hiba-analízis a mérési eredményekben nagy problémákat jelzett a reprezentativitásban, a mérés ismételhetőségében. Első ezek kiküszöbölése az első feladat kell legyen.
Megállapítottuk, hogy a mérési módszerek, eljárások mindegyike túlszabályozott. Olyan előírásokkal találkozunk, ami nehezen tanulható és nehéz betartani. Megállapíthattuk, hogy a mérési módszer tele van a humán hibák lehetőségeivel (a mérő személyzet legjobb akarata ellenére), és például a terhelési sebességről szó sincs a szabványokban. Az alakváltozásnál sem különböztetik meg a rugalmas, a maradó – ezen belül pedig a plasztikus és a tömörödés miatti alakváltozást sehol, hiszen a teherbírás szempontjából csak ezek együttesen – mint summa alakváltozás – érdekesek. A mérési eredmények számítása hibás, mert (1-μ2)∙c szorzat a Poisson tényezőtől függ, azaz nem tekinthető 1,5-nek. Fontos továbbá a mérőórák száma és elhelyezésük is, mert nem ugyanazt az alakváltozást mérik azonos terhelésre – a tárcsa behajlása kimutathatóan más középen, mint a széleken mérve. Hiba-analízis kimutatta azt is, hogy ha ezeknek a megállapításoknak a helytállóságát elfogadjuk, akkor a terhelési ciklusokban a lépcsőnkénti kivárási időt szigorúan kell szabályozni, vagy meg kell szüntetni, vagy egységesíteni szükséges.
Fentiek alapján felvetettük egy lehetséges megoldásként az automatikus mérés alkalmazását, a humán hibák nélküli automata műszer szükségességét, mint a legkevesebb hibával terhelt egyetlen járható utat a mérés innovációjára.
Eddigi tömörség-becslési módszerek a tárcsás mérésből
Tt tömörségi tényező alkalmazhatósága (E2/E1)
A magyar előírásokban a szemcsés alaprétegek egy részénél a tárcsás teherbírás mérésből számítható Tt=E2/E1 „tömörségi tényező” a tömörségi fokra előírt kritériumként jelenik meg. Ennek indoka az, hogy a viszonyítási (referencia) sűrűség, a módosított Proctor vizsgálatban (ρdmax) nem állítható elő a mért anyag/ talaj szemnagysága miatt. A magyar „Kötőanyag nélküli és hidraulikus kötőanyagú burkolatok” ÚME [2] a minőségi követelmények fejezetében a szemcsés rétegek tömörségre az alábbi előírást adja:
| Tömörségi tényező, Tt=E2/E1 legfeljebb | Tömörség, Trρ %, legalább |
| 2,5 | 85 |
| 2,2 | 90 |
| 2,0 | 95 |
| 1,8 | 100 |
Egyértelmű mindenki számára, hogy ez az előírás „jobb híján” született meg, és máig állandó vitákat okoz. Liptay [10] német szakirodalomból [8-9] levont következtetése szerint ez azt jelenti, hogy a tömörödési tényező értékéből még a vizsgálati eredmények középértéke sem ad egyértelmű választ a tömörítés megfelelőségére. Véleménye szerint a Tt=E2/E1 tömörödési tényező a tömörség megítélésére sem a kivitelező saját ellenőrző méréseként, sem a megrendelő átvételi eljárásához nem alkalmas – állapítja meg.
A Tt tömörségi tényező az E2/E1 (avagy s1/s2) arány az első és a második felterhelésből számított érték hányadosa, az MSZ2509-3 szerinti módszerrel mérve. Az FZKA típusú zúzott alapokra nem lehet Proctor vizsgálatot elvégezni a nagy dmax szemcseméret miatt.
Problémának látjuk, hogy az E1 és E2 teherbírási modulust a teljes alakváltozásból számítják – az alakváltozás arányainak vizsgálata nélkül. Belátható ugyanis, hogy a Tt tömörségi tényezőt a tömörödési alakváltozásból kellene meghatározni, nem a teljes alakváltozásból (plasztikus + rugalmas + tömörödési) alakváltozás. Emiatt sajnos egyértelmű, hogy a Tt=E2/E1 arány nem hozható összefüggésbe a tömörséggel, egyezően több irodalmi adattal [10,11]. Más megoldást kell tehát találni a statikus tárcsás mérésből a tömörségi fok meghatározására.
 |
MK Miskolc közelítő tömörségi fok elmélete
A módszert a megközelítő tömörségre a Magyar Közútnál Tamás József [8] dolgozta ki. Nézzük, mit mond ez az elmélet az MSZ2509-3 statikus tárcsás mérésről [4]. A Tt (E2/E1) tömörségi tényezőt ő is következetesen elveti, annak alkalmatlanságát tapasztalva és új módszert keres a tömörség jellemzésére. Javaslata szerint a teherbírás mérésekből a modulusok meghatározása mellett a tömörségi fok is számítható. Ez bizony igen jó dolog lenne, főleg, ha számításba vesszük, hogy a teherbírás mérést amúgy is el kell végezni a minősítéshez. Szerző a következőt mondja: „közismert, hogy a leglazább és a legtömörebb állapot hányadosa kb. 1,4 (azaz √2) körüli érték.
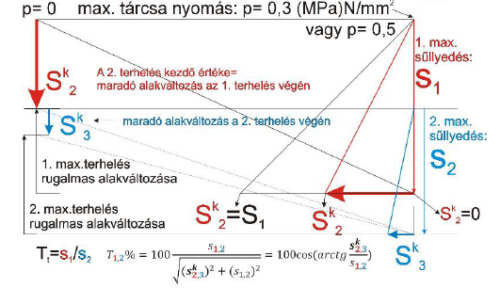
Ha egy derékszögű háromszög hosszabbik oldala si teljes alakváltozás és kisebbik oldala sim maradó alakváltozás, akkor a T% tömörséget a következő a visszaterhelés utáni maradó alakváltozás és az átfogó aránya adja (lásd 2.ábra): T%=100 ∙ [Sim / √(Sim2+Si2)], ahol a nevező a „c” átfogó = √(a2+b2), ez esetben √(sim2+si2)
Az elméletre a következő a magyarázat: ha Sm=0 akkor az átfogó értéke S1, azaz T%=100*1 azaz mivel nem volt tömörödési maradó alakváltozás, emiatt a tömörségi fok 100% (gumi esete). Ha azonban az Sm=S1 azaz a mért maradó alakváltozás a teljes összes alakváltozás, akkor az eset egy laza plasztikus réteg, azaz a mért alakváltozás teljes egészében maradó alakváltozás. Ekkor Sim2=1 és Si2=1 azaz (1+1 ) =2 és T%= 100*(1/√2)= 100*(1/1,41) = 70,7% ami a legkisebb tömörségi fok. A mérésnél minden felterhelési ciklus után a visszaterhelés utáni Sim maradó alakváltozás leolvasása a feltétele ennek a számításnak.
 |
A felvett arányok igazolására több Proctor-vizsgálatot is elemeztünk. Megállapítottuk, hogy a laboratóriumi Proctor-vizsgálat száraz tömeg Gsz = constans modellben számított Proctor minta magasság – Proctor tömörségi fok Dh-Trd% összefüggése alapján a szemcsés anyag legkisebb tömörségi foka 71,7%-ra adódik.
Fenntartásokra int továbbá az a tény, hogy az MSZ2509-3 szabványban pont a mintaként megadott mérésre sem igazolódik ez az elmélet: az első felterhelés (E1=34 kN/mm2) s1m=1,5mm, míg s1=2,01mm. Ebből a fenti képlettel T1%=80,1% lenne. A második felterhelésre sajnos nincs maradó alakváltozás megadva a szabványban (s2m), ezért az már nem számolható. A Tt értéke azonban a bemutatott minta szerint kb Tt=2,5, ami Boromisza Tibor által megadott összefüggés [2] szerint Trr=85%-nak felelne meg. Ebből tehát az elmélet két végpontja (100 és 70,7%) közötti lineáris becslés lehetősége sajnos nem igazolható.
 |
A javasolt módszer a második felterhelés utáni maradó alakváltozásból számítja ki az igazi, a minősítésben figyelembe venni javasolt T2% tömörségi fokot. Nem tudni, miért a második, amikor az eredeti tömörítési állapot (a hengerlés befejezésekor) az első felterhelés előtti állapot volt. A figyelembe vett maradó alakváltozás is az második felterhelés maradó alakváltozása, nem az első + második összege.
Az biztos, hogy a tömörség mérésekor figyelembe veendő alakváltozások összetétele NEM azonos a teherbírási modulus számításához alkalmazott alakváltozással. További gond az elmélet megértésében, hogy – mint minden tömörség mérési módszer – ez is figyelembe kellene vegye, hogy a nedvességtartalma a mért rétegnek mennyire tér el az optimális víztartalomtól. Ha eltér, kell a módosított Proctor vizsgálatból számított nedvességkorrekciós együttható (Trw=ρdi/ρdmax) és az alapján korrigálni kell a tömörségi fok eredményét az optimális víztartalomra.
Gond a fenti elméletben, hogy a módszer azt feltételezi, hogy a mért maradó alakváltozás teljes egésze a réteg tömörödéséből keletkezett, azaz a plasztikus alakváltozás nulla. Ennek előfordulása lehetséges ugyan, de egy elméletbe foglalni nem szabad. Ez sajnos jelentősen befolyásolhatja a pontos végeredményt. Nyilvánvaló továbbá, hogy nem csak a két peremfeltételnek kell teljesülni (eleje – vége), hanem valami elmélet is kellene, hogy a tömörödést hogyan adja ki más módszerrel is, a mérhető kontrollálható közbenső tömörségi fokokat.
Mindezek ellenére kiemelendő és dicséretre méltó a javaslat, mert felkeltette a figyelmet és elsőnek próbálta meg a teherbírás mérési módszert alkalmazni a tömörség újszerű megítélésére. Ki gondolt eddig arra, hogy tárcsás mérésből tömörségi fokot mérjen? Senki a világon – csak egy Magyar Közutas. Nagy köszönet illeti Őt érte.
A statikus tömörségi fok új meghatározása öt terhelési ciklussal
Ahhoz, hogy a statikus teherbírásra alkalmazott tárcsás mérésből a teherbírási modulusok mellett egy teljesen új statikus tömörségi fokot is meg lehessen állapítani, a teljes mérési elméletet és gyakorlatot elemezni kellett. A valóban tömörödést okozó alakváltozás meghatározásán túl a tömörségi fokhoz tartozó egyéb, hagyományos feltételeket is át kellett tekinteni, mint amilyen például a nedvességtartalom és a tömörítési munkavégzés kérdése.
Áttekintendő problémakör a tömörségi fok ás az alakváltozás összefüggésének vizsgálata, alkalmazhatóságának feltételei, hiszen terepi mérésről beszélünk. Az új innovatív eljárás a valós tömörségi eredményt a helyszínen elvégzendő jelentős „többletmunkával” kénytelen meghatározni, ami indifferens akkor, ha a mérés automatizált. A mérési idő növekedése sem egyértelmű és az is indifferens – ha a mérés automatizált. Márpedig ez a célunk.
Az automatizált mérés szoftveres vezérlésű, csak az elhelyezés és az elindítás a kezelő dolga. Emiatt a humán hibák száma kevesebb, a mérés nem fárasztó és szakképzett személyzetet sem igényel. Akkreditálásra csak a mérési módszer algoritmusa szorul.
Az alakváltozások jellegének behatárolása
A mért alakváltozás a teherbírás mérésekben rugalmas és a maradó alakváltozásból tevődik össze. A maradó alakváltozás azonban további két részre bontható, a plasztikus és a tömörödési alakváltozásra, mely utóbbi a levegő eltávozásával jár a V= s + v + l térfogati rendszerből. Emiatt tömörödés méréséhez háromfázisú talajállapot szükséges.
Hogyan láthatnánk meg ezt a többlet információt statikus teherbírás mérésből? Ez a fő kérdés, ami jelenleg tárgyalni és kibontani szeretnénk.
A tárcsás mérésre vonatkozó szabályozások egyike sem kellett kitérjen arra a tényre, hogy az alakváltozás maradó, rugalmas és plasztikus részből áll, mert ezeket a teherbírás mérés egyben kezeli, mint a terhelés hatására bekövetkező alakváltozást. Az angol vizsgálati szabályozás [3] például felterhelésenként leolvasást kér az adott terhelési ponton 1-2-3-4-5-15. percben, azaz a három felterhelésben és 4+6+7 ponton, visszaterheléseknél pedig 4 ponton. Egy mérés akár egy órát is igénybe vehet. Egy felterhelésen tehát 15 percet (900 sec) vesz igénybe a mérés (több leolvasással), azaz a konszolidációt minden terhelésnél kivárják.
A jelenleg ismert szabályozásokat az cikksorozat első részében ismertettük [12], mint az MSZ 2509-3:1989, DIN 18134, ASTM D1194-94, ASTM D1195/D1195M-21, ASTM D 1196 – 93: Reapproved 1997, AASHTO [1981]. AASHTO T 222 – 94, EN1977-2 Eurocode 7 –Part 2, BS 1377- 9 [BS EN ISO 22476-3]. Ezekhez hasonló az olasz CNR BU 146 1992-12, osztrák ÖNORM B4417:1979-12, svéd SN6703176:1998, szlovén TSC 06.720:2003, francia NF P94-117-1:2000-04, spanyol UNE 103808:2006-2 előírások.
Smart Static-Plate teherbírás mérési módszer és az 5-15 sec mérési törvény
Az elmélkedések során kialakult – az általunk javasolt statikus tárcsás tömörség- és teherbírás mérési módszer – egyedülálló, új és szokatlan törvényt javasol követni, mely a teherbírás mérésben is előnyöket biztosít. Az első két felterhelés E1 és E2 ugyan hasonlít a megszokotthoz, de a felterhelés sebességét és a kivárások hosszát pontosan szabályozza. A mérést automatizált kell legyen, azaz a humán hibák egyáltalán nem érvényesülhetnek a mérésben. Az első és második felterheléseket kiegészítettük egy harmadik, negyedik, végül egy ötödik (!!!) felterheléssel, az alábbiakban ismertetett módon és céllal.
- a tárcsát úgy kell kialakítani, hogy az könnyű, de tárcsalemez behajlására kellően érzéketlen legyen
- a tárcsát elhelyezzük 2-3mm homokréteg aláterítéssel. A felület legyen közel vízszintes, a terhelés pedig a tárcsaközép vonalában maradjon
- alkalmazunk p=0,02MPa előterhelést 30sec-ig, majd tehermentesítünk. A pihentető- relaxációs kivárás 15sec után a digitális központi alakváltozás mérő automatikusan lenullázódik és a mérést megkezdődik
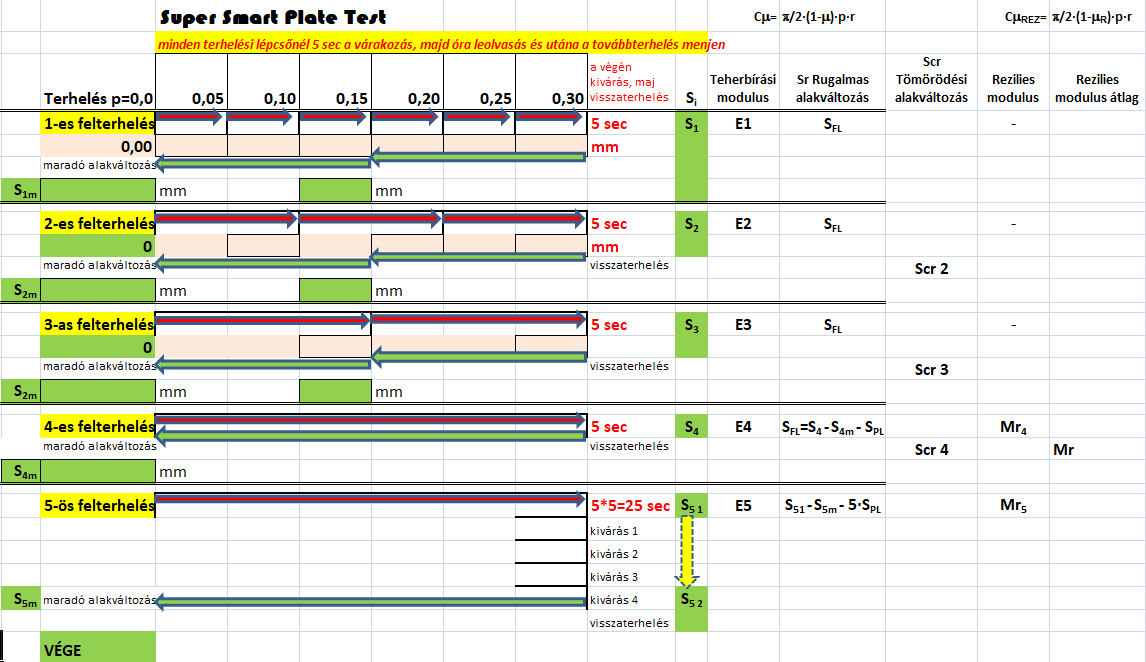
- az 1. és 2. felterhelési ciklus és leolvasás a megszokott módszer szerinti, azaz az első felterhelés D=0,05 MPa (0,5bar) lépcsőkkel, a második D=0,1 MPa (1bar) lépcsőkkel történik. A leolvasás minden lépcsőben 5sec kivárás után történik. Az első ciklusban 6 lépcsőben terhelünk fel, a második terhelési ciklus 10sec terhelési idővel és 5sec kivárás utáni óraleolvasásokkal – három lépcsőben. A visszaterhelés után a maradó alakváltozást is leolvassunk a relaxáció előtt és után
- Minden felterhelés után következő tehermentesítéskor a kötelező pihentetés (relaxáció) 15sec, utána le kell olvasni az alakváltozást (minden felterhelés után). Minden visszaterhelés után kivárunk 15 sec-ot.
- A visszaterhelés mindig egy lépcsőben történik azonos sebességgel, mint felterhelés, a végén 15sec kivárással
- A felterhelés sebessége (automatizált, programozott) 0,05MPa/5sec. egy teljesen automatizált műszer SMART applikációval
- a 3. felterhelést Dp=2*0,15 MPa-ban, azaz két terhelési lépcsővel végezzük az alakváltozás leolvasásával, majd a végén a tehermentesítés után a visszaterhelés után a maradó alakváltozást is leolvassunk a relaxáció előtt és után. (Érezhető a gyakorlott mérőszemélyzetnek, hogy ez már jóval rövidebb idő lesz, mint az első felterhelés volt)
- a 4. felterhelést (Dp=0,3 Mpa-ig) egy lépcsőben végezzük (a terhelési sebesség marad konstans), majd az alakváltozást leolvassuk 5sec kivárás után, majd a visszaterhelés után a maradó alakváltozást is kiolvassunk 15 sec után.
- minden eddigi felterhelésnél lényeges az 5-15sec szabály betartása, azaz minden lépcsőnél a kivárás a leolvasás előtt 5sec, és minden végterhelésnél a kivárás 15sec, azaz NEM várjuk ki a szubjektívnak minősülő „teljes konszolidációt” soha, mert azt majd külön mérjük.
- ezek után, az 5. felterhelés következik, aminek célja pont az eddig kihagyott, de itt már sokkal pontosabban kimérhető plasztikus alakváltozás meghatározása. Egy lépcsőben ismét felterhelünk p=0,3 MPa-ra és leolvassa az automata 5 sec múlva (S51) és utána azonban a terhelést tartva, kivárunk ötszörös 5*5= 25sec-ot, majd az alakváltozást 5 sec múlva leolvassuk (S52). A visszaterhelést egy lépcsőben végezzük el p=0 MPa-ra, ami után 15 sec-et kivárva a maradó alakváltozást is leolvassuk (S5m)
- Lehetőségként a szoftverben fennáll, hogy ha 25sec kevés lenne a plasztikus alakváltozás meghatározására, akkor tovább lehet a végterhelés elérése után (terhelés alatt) kivárni. Ekkor a plasztikus alakváltozás számítása ugyanolyan elven, az egy ciklus időre való átszámítással történhet. A konkrét értékét mindig 5sec-re kell korrigálni.
- A plasztikus alakváltozás jelölése az alapverzió szerint SPL = (S52 – S51)/5 (ahol PL=plastic)
- a tisztán rugalmas alakváltozás jelölése SFL=S4-SPL (ahol FL flexible)
- az egyes felterhelésekben a számított tömörödési alakváltozás a tömörségi fok megállapításához lesz szükséges:
\[ S_{iCr} = S_{i} – S_{FL} – S_{PL} \]
ahol a „Cr” index jelölés compaction rate-et jelöl.
A mérés ezzel befejeződött, következhet a jellemző paraméterek kiszámítása és a tájékoztató értékek megadása.
Megjegyezés: a leírt mérési mód paraméterek egy verziónak tekinthetők, azokat a mérőszoftver beállítás menüben lehet majd változtatni, melyet a verifikálás dönt el. Ugyanakkor megjegyezzük azt is, hogy a mérőszoftver egy verziója és a szenzorok kialakítása lehetővé tesz bármilyen más szabvány szerinti mérést is, mert a processzorvezérelt méréshez más hardverelem nem kell, a szoftver pedig állandó.
Információk, mért adatok a Smart Static-Plate-Test (SPLT) vizsgálatból
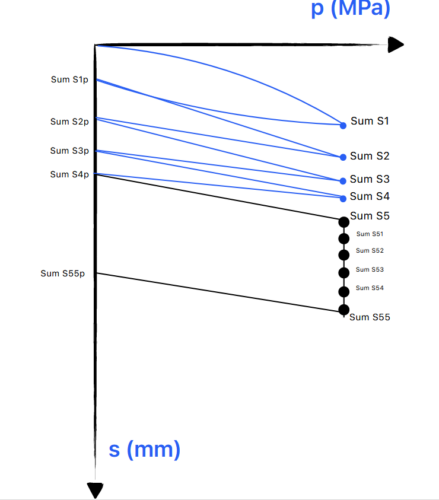
- első – második felterhelésnél a mért alakváltozások süllyedési adatait mérjük és tároljuk
- végterhelések Si (mm) azaz s1, s2,s3, s4, s5-nél mérjük az alakváltozásokat két tizedesre
- visszaterhelések utáni maradó alakváltozások Smi ahol i=1-5 azaz (s1m– s2m – s3m – s4m – s5m) melyet mérünk relaxáció előtt és után, de igazán nem fogjuk használni a számításokban
- rugalmas alakváltozás (SFL) meghatározása a 4. felterhelésből történik SFL=S4– SPL
- a mérés alatt a víztartalmat is kell mérni két alkalommal (szoftveresen)
- az SFL tisztán rugalmas alakváltozás ismeretében meghatározható az MrSt (Helyszíni Statikus Reziliens modulus) értéke, ehhez a mR értéke a Reziliens modulusnál elfogadott Poisson-tényezők listájából választandó
- plasztikus alakváltozás SPL az anyag (talaj) adott telítettség mellett, alacsony vagy nulla a levegőtartalom. A mért érték a felterhelt és leolvasott alakváltozás után 5 sec kivárás (S51), majd újabb 5x5sec=25sec (összesen) plasztikus alakváltozást kell kivárni, majd leolvasni. Azaz az összesen plasztikus alakváltozás ötödét értjük a plasztikus alakváltozás alatt.
- SPL (mm) = (S52 – S51)/5.
- az utolsó felterhelést kizárólag erre a célra alkalmazzuk, feltéve, hogy a tömörödési alakváltozás jelentős részének végbemenetele már nagy valószínűséggel megtörténhetett.
- A tömörödési alakváltozás Scr számítása már ebből adódik és mértéke a teljes alakváltozásból számítjuk (Scr=Si– SFl-SPL).
Új feltétel a Smart Static-Plate-Test vizsgálatnál, hogy a víztartalmat is mérni kell a mérés helyén (MwC% mass-water-content% vagy VwC% Volume-water-Content%) módszerrel.
Fentiekből adódóan tehát a Smart Static-Plate-Test vizsgálatnál egy adott ponton a tárcsa elmozdítása nélkül első felterhelést 6 lépcsőben hajtjuk végre, a másodikat három, azaz a vizsgálat teljes időigénye a szokásos első és második felterheléssel járó mérési időnek kb duplájára tehető. A szabályok betartásával azonban ennek árán igen sok és igen hasznos információkat nyerhetünk igen kis hibával mérve.
Tömörödési alakváltozás mérése Jelölése (Scri mm)
Ábrázolva a felterhelés során mért alakváltozásokat egy görbét kapunk, mely a terhelések hatására bekövetkezett rugalmas, maradó és plasztikus alakváltozások összege. Ebből a számított maradó alakváltozás a tömörödési és a plasztikus alakváltozás. A tömörödéshez tartozó alakváltozás kimérése tehát csak úgy lehetséges, hogy a teljes mért alakváltozásból le kell vonni a plasztikus, majd a rugalmas alakváltozásokat. Ezeket tehát meg kell ismerni a számításhoz.
A mérés során csak a terhelt ciklusvégek alakváltozásaiból dolgozunk, a tehermentesített maradó alakváltozást nem használjuk a számításokban, de leolvassuk (5 sec + 15 sec relaxáció kivárása után).
Kérdésként felmerülhet, hogy a jelenleg az E2 határértékek teljesülésének elbírálására alkalmazott MSZ2509/3 teherbírás mérés 1989-ben milyen feltételezések alapján került elfogadásra és alkalmazásra annak idején. A felület, amin a teherbírást mérjük tömörített, és minősítésre előkészített. Erre felterhelünk p=0,3 MPa-ig egy első E1 terhelést, majd visszaterhelünk. Majd újra felterhelünk még egy ciklust (azaz még egyszer rátömörítünk), amit a teherbírást minősítő E2 értéknek nevezzük.
Ez azt jelenti, hogy azt feltételezhették a mérés elfogadásakor, hogy az épített felület eltakarása után a szerkezet súlya, valamint a további rétegek építése, továbbá az építési forgalom terhelése valószínűleg a második terhelési ciklussal lehet egyenértékű. Ebben az akkori magyar műszaki gondolkodás ma is helytálló, akkoriban pedig élenjárónak tekinthető.
Egy másik feltételezés az lehetne, hogy az E1 értékek olyan nagy szórást mutattak, hogy arra nem lehetett minősítést alapozni. Ennek ellentmond a svájci SN670317b szabályozás, ahol az ME1 érték a minősítő érték (de hát az Svájc), továbbá E1-re minősít az osztrák szabvány is.
Kell-e viszonyítási sűrűség a statikus tömörségi fok méréséhez?
A tömöríthetőségi vizsgálatot négy féleképp lehet elvégezni a jelenlegi EN 13 286-1 EU szabályozás szerint, ez jellemzően a módosított Proctor vizsgálat hazánkban. Lehetséges azonban további három meghatározási módszer is, mint a vibrokalapácsos, vibroasztalos, vagy vibrohengeres vizsgálat. Sajnos nem ismerjük még ezek egymásba való átszámíthatóságát, hasonlóságát, vagy alkalmazásának egyenértékűségét, ezért jellemzően nagy óvatosság látható ezen a területen. Minden ország inkább a korábban megszokott módszereit alkalmazza. A magyar szabályozás [5] a következőt mondja:
 |
Zúzott alapoknál, mint például a folyamatos szemeloszlású zúzott alap FZKA (ÚME 4.2.1.9.pont) a zúzottkő alap tömöríthetőségét nem kell vizsgálni ugyanakkor a LA40 aprózódás megengedett. Az FZKA és a mechanikai stabilizáció termékek besorolásai a Dmax-tól függőek (pl. FZKA0/32, M0/32) és mindkettőre öt csoport van (Dmax 22, 32, 45, 63 és 90mm).
Fentiekből levonható lenne az a következtetés, hogy ha a tömöríthetőségi vizsgálat (egyike legalább) elvégezhető a mechanikai stabilizáción az adott Dmax-nál, akkor elvégezhető kellene legyen az FZKA-nál is. A probléma a Dmax szemcsék zavaró hatása. Egy-két szemet ugyan ki szoktak venni, de 20-30m%-ot nyilván nem lehet – ezzel csak becsapnánk magunkat.
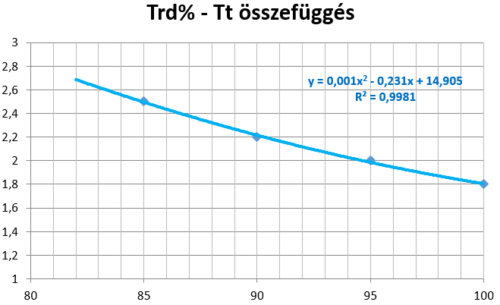
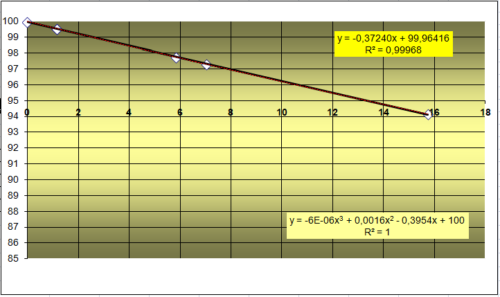
Nincs tehát megnyugtatóan megoldva annak a kérdése, hogy Proctor-görbét, illetve az abból számított nedvességkorrekciós együtthatót (Trw=ρdi/ρdmax) hogyan tudnánk biztonsággal meghatározni. Ez a dilemma okozza azt, hogy az FZKA zúzott alaprétegeknél nem a tömörségi fokkal, hanem a Tt (E2/E1) értékkel minősítjük a tömörséget. Ami ebben a segítség, az a most megadott Tt-Trd% összefüggés (lásd 1.ábra).
Első verifikációs statikus tömörség mérések tapasztalatai
Az UTLAB szövetség keretében 2008 tavaszán az épülő M6 autópályán készült egy összehasonlító vizsgálat a Közlekedéstudományi Intézet és a Magyar Közút lebonyolításában. A kiválasztás szempontja volt az akkreditáltságon kívül a nagy gyakorlat és nagy projektekben való részvételek voltak. A statisztikai értékelésben – ahol lehetett – a minimum, maximum értékeket kihagyták és „korrigált” paramétereket határozott meg Ézsiás [14]. Statikus teherbírás mérés MSZ25009-3:1989 módszerrel kilenc nagy tapasztalatú laboratórium mért 3-3 mérési helyen, meghatározva E1, E2 és Tt értékeket. A statisztikai számítást a Student-féle eloszlással megismételtük azért, hogy azt a későbbi egységes értékeléshez alkalmassá tegyük (3. táblázat). A 90%-os valószínűséggel meghatározott intervallum relatív érték.
| Mérési eredmény E2 | I.szakasz | II. szakasz | III. szakasz |
| labor száma db | 9 (7) | 9 (7) | 9 (7) |
| MIN (MPa) | 52,1 | 22,1 | 60,0 |
| MAX (MPa) | 78,5 | 63,8 | 82,7 |
| Korr. átlag (MPa) | 65,2 | 47,1 | 75,4 |
| Korr. szórás | 8,4 | 9,6 | 7,2 |
| Rel. szórás % | 13% | 20% | 10% |
| SZÁMÍTOTT (Új) ±Δ (Student=1,943, α=0,1 és ν=n-1) | ± 9,5% | ± 14,7% | ± 7,3% |
E szerint az E2 teherbírási modulus mérési megbízhatósága akár ±15% is lehet, a szerző által alkalmazott korrigálások (min-max elhagyása) ellenére. Megjegyzendő, hogy minősítéskor legálisan a min-max értékek nem hagyhatók el. Szerző megjegyzi továbbá, hogy a teljes mérési idő 1,5 perctől 14 percig terjedt, azaz eltérése igen jelentős volt az akkreditált laborok mérései ellenére.
Második verifikációs mérés 8-as elkerülő út Veszprém 2021
Az ÚTLAB szervezésében 2021-ben volt egy másik összemérés is, egy épülő híd-háttöltésen a 8-as út mellett. Ez volt az első lehetőség az 5 ciklusos statikus tömörség – teherbírás mérések kipróbálására, melyért ez úton is köszönetet mondok minden résztvevőnek és a szervezőnek.
A verifikációban 11 db akkreditált laboratórium vett részt, nagy gyakorlattal rendelkező laboratóriumi munkatársakkal. Az átadott „kotta” alapján elvégezték a kísérleti öt ciklusos mérést, elsőként a világon. A mérés célja az volt, hogy a statikus tömörségi fok meghatározhatóságát az új elmélettel ellenőrizzük, másodsorban pedig az, hogy az ötciklusos SPLT mérési módszerrel kapott teherbírási (E2) és a TrESPLT% helyszíni relatív statikus tömörségi fok értékek ismételhetőségét, megbízhatóságát kiderítsük.
| Mérési eredmény E2 | A szakasz | B szakasz | C szakasz | A+B+C |
| labor db | 10 | 11 | 11 | 32 |
| MIN (MPa) | 67,0 | 83,5 | 88,1 | 67,0 |
| MAX (MPa) | 109,0 | 131,3 | 128,6 | 131,3 |
| átlag / várható érték (MPa) | 93,0 | 105,2 | 107,1 | 102,1 |
| szórás | 12,3 | 11,8 | 12,6 | 13,4 |
| Rel. szórás % | 13,2% | 11,2% | 11,7% | 13,1% |
| Mérési megbízhatóság ±Δ% (Student=1,833, α=0,1 és ν=n-1) átlaghoz képest | ± 7,7% | ± 6,1% | ± 6,4% | ± 3,9% |
azaz az E2 teherbírás-mérés megbízhatósága kedvezőbb. Megjegyzendő, hogy itt a min-max értékeket nem hagytuk el, mint az előbbi táblázat tette. Fentiek szerint – bár a mérési megbízhatóság javult – az SPLT tárcsás teherbírás mérés további fejlesztése lesz szükséges és vélhetően az egyetlen megoldás az lesz, hogy a humán hibák teljes kiküszöbölését el kell érjük.
| Mérési eredmény | A szakasz | B szakasz | C szakasz | A+B+C |
| labor db | 10 | 11 | 11 | 32 |
| MIN (%) | 93,4 | 95,6 | 95,3 | 93,4 |
| MAX (%) | 98,5 | 97,8 | 98,2 | 98,5 |
| átlag / várható érték % | 96,0 | 97,1 | 96,8 | 96,6 |
| szórás | 1,5 | 0,7 | 0,8 | 1,1 |
| Rel. szórás % | 1,6% | 0,7% | 0,8% | 1,2% |
| Mérési megbízhatóság
±Δ% (Student=1,833, α=0,1 és ν=n-1) átlaghoz képest |
± 0,9% | ± 0,4% | ± 0,5% | ± 0,4% |
A fenti táblázatban – a statikus tömörségi fok mérésnél – az ismétlési mérések megbízhatósága kedvezően alacsony terjedelmet mutat. Ismétlési, azaz más műszerrel, más személyzettel, más laboratórium által végzett mérés, egy mérési metódussal. Javasolt a kísérlet folytatása néhány laboratórium bevonásával, a mérési szám jelentős növelésével, homogénnek tekintett szakaszon, a párhuzamos mérések megbízhatóságának meghatározására. Kedvező esetben előírható lehetne a párhuzamos mérés kötelező alkalmazása és átlag képzése a minősítéshez.
 |
A tömörítési munka eltérése esetén szükséges lehet további korrekció, mint a ”k„ a rétegvastagság eltérése miatti korrekció (LTP), valamint az optimális víztartalomtól való eltérés miatt alkalmazandó Trw nedvességkorrekció. Ezek a korrekciók a dinamikus tömörségmérés elméletéből már jól ismertek [17, 18], és itt is alkalmazhatók.
Statikus tömörségi fok számítása
Az a SPLT tárcsás méréssel a visszaterhelés után mért maradó Smi alakváltozás (mint jeleztük) nem alkalmas a statikus tömörségi fok meghatározására, mert a tömörödés miatti alakváltozás (S1cr) mellett tartalmazza a képlékeny (SPL) azaz a plasztikus alakváltozást is. Ezért a maradó alakváltozást a következő elmélkedésből teljesen kihagytuk.
Ugyanakkor azonban az első ciklus végterhelésére is számítható:
\[ S_{1CR} = S_{1i} – S_{PL} – S_{FL} \]
E mellett mindig teljesül, hogy S1cr≤ S1m azaz sem a maradó, sem a rugalmas alakváltozás nem számít bele a tömörödésbe. Az első terheléskor S1cr, majd S2cr a mért tömörödési alakváltozás az i=2 azaz második felterheléskor, S3cr a mért alakváltozás a harmadik felterheléskor, S4cr = a mért alakváltozás a negyedik terheléskor és S4cr az ötödik felterheléskor. Nyilvánvaló, hogy a tömörödési alakváltozás a ciklusok számának emelkedésével a nullához tart (Sicr ►0)
Számítható a Dm deformációs mutató (az MSZ15846 dinamikus tömörségi fok elméletéből átvéve), Dmi= Sicr ami tisztán tömörödési alakváltozás. A tárcsát az öt ciklus között nem mozdítjuk el és minden újabb felterhelés újabb tömörödést okoz, azaz egyre inkább növekvő tömörségi fokot kapunk. (TrESPLT1%, TrE SPLT2%, TrE SPLT3%)
Mindebből a helyszíni relatív Statikus PLT Tömörségi Fok terhelési ciklusonként:
\[ TrE\%_{PLTi}=100-1,25ΦD_{mi} \]
ahol F az MSZ15846 szerint értelmezett módosított Proctor-vizsgálatból számított alakváltozás- tömörségi fok összefüggés meredeksége (0,38±0,02), ahol Dmi definícióját lásd fentebb.
A statikus tömörségi fok természetesen függ a talaj nedvességtartalmától. Trw értéket a módosított Proctor görbéből számítjuk Trw=ρdi/ρdmax kifejezésből. Esetleges korrekció „k” továbbá lehetséges a nagyszámú összehasonlító vizsgálatok statisztikai feldolgozása alapján.
Fentiek alapján megállapítható, hogy
- a statikus tömörségi fok számítása során figyelembe vett alakváltozás más, mint a statikus teherbírási modulus számításakor figyelembe vett alakváltozás.
- emiatt a STATIKUS TÁRCSÁS TÖMÖRSÉG- és TEHERBÍRÁS mérés módszerét eleve úgy kell kialakítani és végrehajtani, hogy az alkalmas legyen mind a hagyományos statikus teherbírási modulus (E2), mind a statikus tömörségi fok meghatározására egyetlen méréssel
- kizárólag automata mérési mód és műszer elkészítése és alkalmazása lehet a cél
Az alakváltozás összetétele (rugalmas, plasztikus, tömörödési- alakváltozás) a különböző talaj-anyagoknál nagyon különböző lehet, annak ellenére, hogy a tárcsa elmozdítása nélkül, ugyanazon mérésből számítjuk mindkét jellemzőt.
A statikus tömörségi fok mérést öt felterheléssel kell elvégezni, melyből az utolsóval a plasztikus alakváltozást határozzuk meg, az utolsó előttivel pedig a rugalmas alakváltozást. Fontos, hogy a felterhelés (és visszaterhelés) sebességét is szabályozzuk automatikus, processzorvezérelt méréssel. A statikus tárcsás teherbírás és tömörségi fok mérést p=0,3 N/mm2 végterhelésig javasoljuk végezni, de alkalmas lehet p=0,50 MPa határig is, melynél vélhetően egy újabb szorzót kellene alkalmazzunk.
A mérési idő irreleváns, ha a mérés teljesen automatizált (de kb. 6-8 perc), mert emberi közreműködés nem szükséges – az elindítást kivéve. A berendezés részei a bordás-tárcsa és mérőkeret, mely könnyű – de igen erős, szénszálas kevlár anyagból készül. A műszer felállítása nem igényel szakszemélyzetet, így akár a kivitelező (QA) is elvégezheti.
A vezérlést és a mérési adatok tárolását és továbbítását okostelefonos applikációval is végezhetjük, bluetooth kapcsolattal. A felterhelés és visszaterhelés sebessége szabályozott és konstans. Lehetőség emiatt, hogy a szoftver nem csak a STATIKUS TÁRCSÁS TÖMÖRSÉG – és TEHERBÍRÁS mérést, hanem más szabványok szerint mérést is le tudja bonyolítani (DIN18134, ASTM D1196, CRD-C 655-95, AASHTO T222), ezzel a műszer piacképessége és vevőköre jelentősen növelhető.
A statikus teherbírás – tömörségi fok első mérések tapasztalatai
Teherbírási modulusok meghatározása az SPLT mérésből
E1 (MPa vagy kN/mm2): az épített réteg szerkezeti réteggel terhelt várható teherbírási modulusa, ha a terhelést legalább 0,3MPa-ig folytatjuk és utána tehermentesítünk. Alternatíva lehet a p=0,5 kN/mm2 terhelési határ nem csak pályaszerkezeti rétegekre, hanem akár talajokra, szemcsés anyagokra is. Az alakváltozás tartalmazza a plasztikus és a rugalmas, valamint a tömörödés miatti összes alakváltozást – mely az adott terhelési idő alatt megy végbe. Szubjektív hibáktól mentes automatizált mérés, ezért ismételhetősége várhatóan jó és nem függ a választott labortól sem.
E2 (MPa vagy kN/mm2): a tehermentesítés és relaxáció után a terhelést újabb ciklussal folytatjuk. Tartalmazza a plasztikus és a rugalmas, valamint a tömörödés miatti összes alakváltozást.
E3 MPa vagy kN/mm2: a harmadik és negyedik felterheléskor kimutatható a rugalmas alakváltozás a vélhetően végbement statikus tömörödés után, az épített és már kétszer felterhelt és tehermentesített rétegen, ahol valamennyi felterheléskor azt 0,3 (vagy 0,5) MPa-ig folytattuk.
E4 (MPa) egy menetben újra felterhelt mérés, a rugalmas alakváltozás biztos kimutatására. E3és E4 átlaga (vagy E4-E5 átlaga, esetleg E3-E4-E5 átlaga) vélhetően egy rugalmasságra vonatkozó jó jellemző lesz, mely jellemezheti a reziliens (tisztán rugalmas) modulust is.
A tisztán rugalmas modulus egy anyagjellemző és a Hook-féle törvényt követő Young-féle modulussal is várhatóan egyező lehet (s=E∙e).
Valamennyi fenti esetben betartjuk lépcsőnkként az 5sec leolvasás előtti kivárást és a 15sec-es relaxációs kivárási szabályt, valamint a konstans terhelési sebességet.
E5 (MPa) a kimutatott rugalmas alakváltozás és a már vélhetően végbement statikus tömörödés után, a már négyszer felterhelt és tehermentesített rétegen – a tárcsa elmozdítása nélkül. Az ötödik felterhelés után kivárandó idő azonban 5*5=25 sec, ami kizárólag a plasztikus alakváltozás meghatározására szolgál, ezért mért értékét majd öttel osztjuk, hogy egy 5 sec kivárással arányos legyen.
A teherbírás mérésben annyi a szerepe, hogy E4 és E5 értékek átlagolhatók és így a rugalmas alakváltozásból számítható a statikus reziliens modulus értéke, mely átlagolással még pontosabbá tehető.
A teherbírás számítása változatlan:
\[ E_{i} = \frac{c(1-μ^{2})pr}{S_{i}} \]
Természetesen a jelenleg ismertetett értékek programozhatók és változtathatók, ezeket ezért V1.0 verziónak kérjük tekinteni.
Mérés adatsora
A mérési eredmény egy lehetséges adatsora a TEXT-file, mely summázott formában tárolja a mért mm alakváltozás 100-szorosát és a hozzá tartozó nyomás értékét. A kivárások időpontja ciklusonként konstans, ezért azok a mérési-feldolgozási szoftver része, nem mérési eredmény.
A teherbírási modulusok számításakor a teljes Si alakváltozást (maradó-, rugalmas- és plasztikus alakváltozásokat együtt) kell figyelembe venni.
Egyéb feldolgozáshoz (pl. ágyazási együttható) – a későbbiekben – javasolt inkább a folyamatos mintavétel pl. Pi (bar∙100) és Si∙100) szekundumonként mérve és lerakva, mert annak fejlesztési lehetőségei és teljesen nyitottak.
Az STX (Start text után a mérés alapadatait, majd a mérés során mért summa adatokat rögzítjük. Ezt mutatjuk be egy V.0 verziójú mintán:
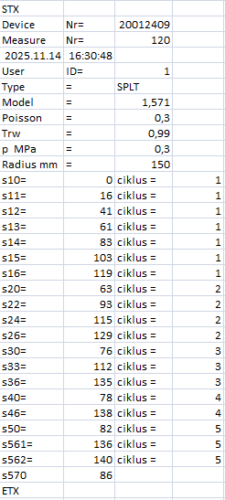 |
A statikus tömörségi fok számítása a SMART statikus tárcsás mérőeszközzel
A statikus tömörségi fok meghatározásakor a tömörödési alakváltozást vesszük csak figyelembe (lásd 2. képlet) Sicr = Si – SiFL – SiPL
Ehhez tudni kell az ötödik ciklusból meghatározott plasztikus alakváltozást és a negyedik ciklusból meghatározott rugalmas alakváltozást.
Az így számolt TREiPLT tömörségi fok is csak az adott nedvességtartalom mellett, adott anyagra és adott rétegvastagságra megadható statikus relatív helyszíni tömörségi fok % (TREiSt), melyet még korrigálni kell az optimális víztartalom függvényében a Trw nedvességkorrekciós tényező értékével:
\[ T_{iSPL}\% = T_{rw} T_{REiPLT} \]
ahol Trw = rdi/rdmax az anyag típusvizsgálatából (vagy alkalmassági) meghatározott Proctor görbéből számítva
a rdi a mért wt terepi (természetes) víztartalomhoz tartozó módosított Proctor vizsgálatban megállapított görbéből számított száraz testsűrűség hányadosa
Trw számítása:
\[ T_{rw}=\frac{\rho_{di}}{\rho_{dmax}}(\le\ 1,00) \]
Fentiek szerint a TriSPLT% STATIKUS TÁRCSÁS TÖMÖRSÉGI FOKOT minden egyes felterhelésből számítjuk, azaz részenként, miközben a terhelési ciklusok során láthatóan tömörödik is a mért réteg. Ez mutatja, hogy az adott terhelési ciklusban milyen a tömörségi fok, illetve a következőben továbbtömörödés történt-e.
A mért terepi tömörségi fok így a teherbírás SMART-SLPT vizsgálatból a korrigált maradó alakváltozásból számítható a következő módon:
Dm1 = S1mcr az 1. ciklusban elért tömörségi fokhoz
Dm2 = S2mcr a 2. ciklusban elért tömörségi fokhoz
Dm3 = S3mcr a 3. ciklusban elért tömörségi fokhoz
A HELYSZÍNI RELATÍV STATIKUS TÁRCSÁS TÖMÖRSÉGI FOK:
TrESPL\%= 100 – 1,25*F*Dmi
Ahol F az MSZ15846 szerint értelmezett EN 13286-2 szerinti módosított Proctor-vizsgálatból Gsz=const modellben számított alakváltozás – Proctor tömörségi fok lineáris összefüggésének meredeksége.
 |
A STATIKUS TÁRCSÁS TÖMÖRSÉGI FOK a nedvességtartalmat és a hatásmélységet figyelembe vevő alábbi képlettel számítható.
\[ T_{riSPL}\%=T_{rw} T_{REist} \]
ahol Trw nedvességkorrekciós együttható wopt-nál 1,00 és jobbra is, balra is – mindkét ágon kisebb. számítása:
\[ T_{rw} = \frac{ρ_{di}}{ρ_{dmax}} \]
SPLT statikus tömörség-teherbírás tárcsás mérő műszer kialakítási elve
A fő egységek eltérőek, a részegységek kialakítása kissé eltér az eddigi kézi felterheléstől és műszertől. A bordás-tárcsa szénszálas kevlárból lehet kialakítva, egy univerzális kitámasztó – leolvasó rendszerrel. A mérőléc szénszálas kevlárból, vagy alumínium teleszkópos rúdból lehet kialakítva, ami egy mozdulattal nyitható és elhelyezhető (lásd 4. ábra).
A tárcsa közepén van a hidraulika henger fogadógödre. Egy lítium akkus könnyű terhelő-tápegység (ON/OFF kapcsolóval) és hidraulika szivattyú csatlakozik a hidraulika hengerhez és egy vezeték a keretléchez. A terhelő-tápegység bluetooth-on kapcsolódik a SMART okostelefonon elhelyezett mérő- vezérlő – adattároló – adattovábbító applikációhoz, vagy ugyanabban a hordozótáskában van elhelyezve, mint a hidraulikaszivattyú.
 |
Az applikáció a mért adatokból azonnal képes jegyzőkönyvet előállítani a digitális adatokból és azt azonnal lehet továbbítani a minőségfelügyeletnek. Ez tartalmazhatja a határértékeket is és azt, hogy Megfelelt /Nem felelt meg a mérés. Ennek alapján az eltakarási engedély azonnal kiadható. Fentiek azt jelentik, hogy a mérés papírtakarékos, gyors, és már a mesterséges intelligencia alkalmazására készíti fel az építőipart.
Tárcsás teherbírás mérés kialakítása
A megoldás egy új, automatikus mérési módszer, ami a humán erőforrás hibáit a lehető legnagyobb mértékben kiküszöböli. A teherbírás mérést a XXI századba kell helyezni, melynek elemei:
- kevlár-szénszálas tárcsa alkalmazása, megfelelő merevítéssel kialakítva, bordázott csúszásmentes talppal,
- lézeres távmérő alkalmazása alakváltozás mérésére
- távolságmérő elhelyezése a tárcsában (felfelé mérve)
- teleszkópos referencialéc alkalmazása középen gravitációs, önbeálló referencialappal
- egyenletes nyomásváltozású hidraulika pumpa,
- kétutas hidraulika henger, a felterhelési sebesség és tehermentesítési sebesség megfelelő szabályozhatóságára
- humán beavatkozás teljes kizárása szoftveres beállításokkal, AI alkalmazása
- fentiek megvalósításával ismételhető, talajra jellemző teherbírás-mérési eredmények
A megvalósítás részletei
- mérőalagút a tárcsatoronyban, a hidraulika henger alatt
- igen gyors felállás a méréshez, egygombos mérés-indítás
- referencialéc teleszkópos, kihúzható, akasztólábas és középen önbeálló vízszintes leolvasó lemezzel
- akkreditálható mérési program, mely humán-hiba mentesen kialakítható
- mérőszoftver specifikáció és applikáció, vezeték nélküli adattovábbítással
- mérési jegyzőkönyv digitális adatokból, azonnali adattovábbítás a felügyelet részére
- mérési eredmény értékelése alkalmas legyen a térinformatikai feldolgozásra
- mérési hely GPS pozíciójának meghatározása
- teherbírási mérési módszer elméleti kidolgozása (specifikáció)
- teherbírási mérési módszer verifikációja (kontroll)
- statikus tömörségi fok és teherbírási modulus, ágyazási együttható és CBR% és víztartalom mérése
- statikus tömörségi fok és teherbírás mérési-, nedvességtartalom mérési módszer verifikációja
- ismételhetőség és megbízhatóság több anyagtípuson, több terhelési határral, eltérő szerkezeti rétegekre
- statikus tömörségi fok mérésének lehetősége a módosított Proctor-vizsgálat anyagjellemzőiből
- statikus mérés és módosított Proctor vizsgálat munkavégzése
- „QC” mellett a „QA” célú mérési feladatokra történő kiterjesztés
- elérhetőség KKV (SMA) vállalkozások részére is
Terhelő automatika kialakítása
- hidraulikus pumpa, adott (0,1bar/sec) sebességgel, adott kétutas hidraulika dugattyúhoz tartozó térfogatú hidraulikaolaj pumpálására (vagy sebességszabályozással ellátott visszaterheléssel, ekkor NEM kell kétutas hidraulika)
- kisméretű hidraulika szivattyú a szükséges fel/le terhelés és terhelési sebesség biztosítására
- kétutas hidraulika henger, mely alkalmas a felterhelés és visszaterhelés egyforma (választott) sebességének biztosítására
- nyomásmérő szenzor (pl. Tematec DMP331, vagy hasonló képességű)
- mérőszoftver által vezérelt processzoros mérés-vezérlés
- 12V vagy 24V Lítium-vasfoszfát akku tápellátással
A kialakítás változtatása még lehetséges, a megvalósíthatóságot akartuk bemutatni fenti kialakítással.
MÉRŐ AUTOMATIKA
- Távolságmérő tapintásmentes, lézeres, ezred milliméter pontosságú, gyors, pontos mérés ezred mm pontossággal
- Nedvességtartalom mérés a tárcsa aljába épített
- IP67 védettség van a terepi használat miatt
- BT-192 Bluetooth adattovábbításra (alternatív)
- GPS pozíció meghatározás (LAT-LON),
- Mobil wifi,
azonnali adattovábbítás, mérési jkv továbbítás informatikai feldolgozásra
 |
Mérés részletes bemutatása
Általános jellemzők: átszámítások, nyomás 1bar=0,986 atm=100kPa=0,01MPa
terhelési sebesség fel/le sebesség v=0,1bar/sec >> 10kPa/sec >> 0,01MPa/sec-ig.
terhelési lépcső – egy ciklusban lépcsőkkel történő terhelés, kivárással és leolvasással.
Terhelés és visszaterhelés öt ciklusban, egymás után történik. Az első ciklusban a felterhelésben 6 terhelési lépcső van, a másodikban három, a harmadikban kettő, a negyedik és ötödikben nincs lépcső (mely szükség esetén a kialakítás, és szoftver alapján változtatható), és végig egyenletes terhelés történik. Terhelés és visszaterhelés öt ciklusban történik, folyamatos nyomás- alakváltozás méréssel.
ELŐTERHELÉS – PreLoading 0,02MPa/30 sec kivárás, vissza és 5s kivárás
TERHELÉS – LOADING p=0,3MPa-ig
1.ciklus: lépcső 6, felterhelés v=0,1bar/sec, t= 5 sec, kivárás leolvasás előtt 5sec. Felterhelés 1.ciklus vége 3 bar (0,3 MPa). Visszaterhelés után a pihentetés 15sec, leolvasás visszaterheléskor és a pihentetés után 5sec-dal is.
2.ciklus lépcső 3 lépcső, felterhelés v=10kPa/sec, azaz v=0,1bar/sec, t= 10 sec, kivárás 5sec. Felterhelés 2.ciklus vége 3 bar (0,3 MPa). Adat p-s 60db, mérési idő 60 sec + vissza 60 sec, (szoftver beállításától függően)
pihentetés 15sec, leolvasás visszaterheléskor és a pihentetés után 5sec-dal is.
3.ciklus lépcső 2 db, felterhelés v=0,1bar/sec, t= 15 sec, kivárás 5sec. Felterhelés 3.ciklus vége 3 bar (0,3 MPa). Adat p-s 60db, mérési idő 30 sec + vissza 30 sec, (szoftver beállításától függő)
pihentetés 15sec, leolvasás visszaterheléskor és a pihentetés után 5sec-dal is.
4.ciklus lépcső 1db, felterhelés v=0,1bar/sec, t= 30 sec, kivárás 5sec. Felterhelés 3.ciklus vége 3 bar (0,3 MPa)
adat p-s 60db (60 sec) + vissza 60 sec, (szoftver beállításától függően)
pihentetés 15sec, leolvasás visszaterheléskor és a pihentetés után 5sec-dal is.
5.ciklus lépcső 1db, felterhelés v=0,1bar/sec, t= 30 sec, kivárás 5sec. Felterhelés 3.ciklus vége 3 bar (0,3 MPa). Adatpár p-s 30db + kivárás leolvasás előtt 5 sec, vissza 30 sec, (szoftver beállításától függően). Ez után új paraméter-mérés történik: terhelt állapotban kivárunk5x5=25 sec-ot, leolvasás, majd visszaterhelés 30 sec, pihentetés 15sec, leolvasás, leolvasás visszaterheléskor és a pihentetés után 5sec-dal is.
SPLT MÉRÉS VÉGE.
Az SPLT mérés összesen 8-10 perc körüli, automatikus, emberi beavatkozás nélküli. Végén protokoll küldés beállított mail címre jkv/pdf.
PRINTER – egy lehetőség igény esetén, p-s grafikonnal (x=p MPa, y=s mm) hőpapíros, SEIKO DPU-H245 vagy hasonló, bármilyen típus megfelel. Beépített a litium-akku, a hidraulika motor mellett, a vezérlő elektronika és adattároló (pld kivehető SSD) mellé helyezve.
Lehetséges párhuzamos – humánmentes – mérések
2 tárcsamérettel előre húzva, kitámasztva újabb vizsgálat, ami párhuzamosnak számíthat. Átlag, és protokoll küldés beállított mail címre jkv/pdf
Lehetséges ismételhetőségi – humánmentes – mérések
Másik műszerrel, másik pl. független labor egy időben mérhet a kivitelezői laborral, két tárcsa egymás mellett
Alternatíva lehetséges a leolvasásokban is. Másik megoldás lehet ugyanis az a mérési adatrögzítési megoldás, ahol minden sec-ben történik egy alakváltozási és egy terhelési érték leolvasás. Ez az adatpár p-s például 6 perc alatt 6∙60=360db adat ciklusonként majd egy visszaterhelés +360db (szoftver beállításától függően). Előnye a módszerbnek, hogy a 1,25mm-hez tartozó terhelés is (ezzel az ágyazási együttható is) meghatározható egyetlen méréssel. Nyilván ez a megoldás összehangolandó a hidraulika (pneumatika) hengermozgásának sebességével (térfogatával) is.
Nedvesség-tartalom mérés
A víztartalom mérés a statikus tárcsás tömörség mérési módszernél is nélkülözhetetlen. A laboratóriumi módszer mellett az alkalmazható a pontos és gyors mérési módszer a dielektromos állandó mérésének elvén történő nedvességmérési módszer, mely lehetséges oly módon, hogy a kevlár anyagú tárcsa talpán elhelyezett antennát alkalmazunk, A dielektromos-állandó elvén működő nedvességtartalom mérési eljárással nagy mérési tartomány (1-35m%) mellett, egy viszonylag szűk 1m% pontossági követelmény is teljesíthető.
A víz dielektromos állandója olyan nagymértékben különbözik minden más anyagétól, hogy emiatt a víztartalom közvetett mérése lehetségessé válik ilyen módszerrel. A kapacitív mérőcellás műszerek jellemző méréshatára 1-16% közötti és sokszor keveredik, hogy ez térfogatos, vagy tömegszázalékos eredmény-e egyáltalán. Pontos mérésre kalibrálva ezek a műszerek ezért nem kaphatók, gyári beállításuk ellenőrző mérése pedig igen komoly eltéréseket mutat. Felhasználói hangolásuk, finom kalibrálhatóságuk általában nem megoldott.
Arra a véleményre jutottunk, hogy először a fogalmak terén kell tiszta helyzetet teremteni, átláthatóvá és érthetővé tenni a mérés logikáját, mértékegységét (VwC% és MwC%). Jó példa erre a betontechnológia, ahol a tömegarányos száraz keverék-tervezés mellett a víztartalmat már liter/m3-ben tervezzük meg és a v/c tényezőnél döntő ennek ismerte. Ezt a VwC%*10 értékkel, mint liter/m3 tudjuk jellemezni, ami igen nagy dolog a stabilizációknál is, és a keverőtelepi cementes keverékeknél is.
Előkisérleteink szerint lehetséges a kevlár tárcsa alsó felén elhelyezett fém hurokkal a dielektromos állandót mérni (lásd 1. kép) és ebből a VwC% (volume water contant v%) és a hézag nélküli anyagsűrűség ismeretében MwC% (mass water contant m%) értékét meghatározni.Ez a mért anyag módosított Proctor vizsgálatának ismeretében lehetővé teszi a Trw nedvességkorrekciós görbe meghatározását és ezzel a munkavégzési koefficiens értékével korrigált CWC munkavégzési korrekcióval a nedvességkorrekciós együtthatóval számított Statikus Tömörségi fokot. A lehetséges víztartalom mérés kialakítás a tárcsa alján is elképzelhető, melynek verifikációját mutatja a 6.ábra.
A nedvességtartalom meghatározása a nedvességkorrekciós együtthatóhoz szükséges. Ugyanakkor ki fogunk térni a 3 cikkünkben arra is, hogy a szükséges módosított Proctor vizsgálat hogyan egyszerűsíthető, mi módon számítható a Proctor- görbe pontosan.
 |
Balesetveszély sikeres csökkentése
A mérés fejlesztésében figyelemmel kell lenni a korábbi teherbírás mérés veszélyeinek minimalizálására is. Az automata mérés ezt is képes biztosítani. Veszélyes volt a mérőeszköz felállítása, és maga a mérés elvégzése is. Előfordult korábban a terhelés során kivágódó közgyűrű, támasz-magasító, vagy az ellensúly biztosító gép lebillenése. Ezeket a veszélyeket, a szükséges munkavédelmet az összes mérési szabvány elegánsan a mérést végzők hatáskörébe utalja, mint a mérőszervezetnél szabályozandó balesetvédelmi kérdést.
A lehetséges balesetek kivédésre is kitérő fejlesztést tartottunk szükségesnek, mely eleve kizárja a sérüléseket.
Összefoglalás
Célunk egyrészt a tárcsás teherbírás mérés problémáinak elemzése volt, mely alkalmas lehet a megoldás tesztelésére. Megadtuk a javasolt új automata műszer és mérési mód egy lehetséges változatát és alkalmazásának vizsgálatát – mint lehetséges módszert – egy új statikus tömörségi fok meghatározására.
Áttekintettük a korábban alkalmazott, tömörséget jellemezni kívánó megoldásokat, mint a tömörségi tényező és a MK megismert T1-T2% elmélete. Megállapítható, hogy a Tt nem alkalmas a tömörség jellemzésére, sem az elméleti megfontolások, sem a szakirodalom alapján, ugyanakkor megoldás szükséges arra, hogy ilyen esetekben is lehessen tömörséget előírni, mérni és minősíteni. Más megoldást kell tehát találni a statikus tárcsás mérésből a tömörségi fok meghatározására.
A MK módszerét részleteiben áttekintettük és más utat javasoltunk a tömörödési alakváltozás értelmezésére. Ennek ellenére a kísérlet kiemelendő és dicséretre méltó, mert felkeltette a figyelmet. Elsőnek próbálta meg a statikus mérési módszert tömörség újszerű jellemzésére alkalmazni. Ki gondolt eddig arra, hogy tárcsás mérésből tömörségi fokot mérjen? Senki a világon – csak egy Magyar Közutas. Nagy köszönet illeti Őt érte.
A mért alakváltozás a teherbírás mérésekben is a rugalmas és a maradó alakváltozásból tevődik össze, de a teherbírás mérésben együtt vesszük figyelembe. A maradó alakváltozás további két részre bontható, a plasztikus és a tömörödési alakváltozásra, mely utóbbi a levegő eltávozásával jár a V= s + v + l térfogati rendszerből. Ezért a Tömörségi fokot csak a tömörödési alakváltozás jellemezi.
Az általunk javasolt statikus tárcsás tömörség- és teherbírás mérési módszer – egyedülálló, új és egy szokatlan törvényt ajánl. Az első két felterhelés E1 és E2 ugyan hasonlít a megszokotthoz, de a felterhelés sebességét és a kivárások hosszát pontosan szabályozza. A mérés automatizált, azaz a humán hibák egyáltalán nem érvényesülhetnek a mérésben. Az első és második felterheléseket kiegészítettük egy harmadik, negyedik, végül egy ötödik felterheléssel, a tanulmányban részletesen ismertetett módon és céllal. A humán hibák nagyságának igazoló kimérésére összehasonlító mérések előnyösen alkalmazhatók, mely egyben az automatizált mérés előnyeit is igazolja a mérőszemélyzetnek.
Az új eljárás a valós tömörségi eredményt a helyszínen kis jelentős időtöbblettel, de jelentősen kevesebb fizikai munkával határozza meg. A negyedik –ötödik felterhelést egy lépcsőben végezzük. Minden felterhelésnél lényeges az 5-15sec szabály betartása, azaz minden lépcsőnél a kivárás a leolvasás előtt 5sec, és minden végterhelésnél a kivárás 15sec azaz NEM várjuk ki a szubjektívnak minősülő „teljes konszolidációt” soha, mert azt külön megmérjük.
Az ötödik felterhelés célja pont az eddig kihagyott, de itt már sokkal pontosabban kimérhető plasztikus alakváltozás meghatározása. Egy lépcsőben ismét felterhelünk p=0,3 MPa-ra leolvassuk 5 sec múlva (S51) és utána a terhelést tartva, kivárunk pl ötszörös 5*5= 25sec-ot, majd az alakváltozást 5 sec múlva leolvassuk (S52). A visszaterhelést egy lépcsőben végezzük el p=0 MPa-ra, ami után 15 sec-et kivárva a maradó alakváltozást is leolvassuk.
Ezek alapján a számítások elvégezhetők, melyet a tanulmány részletesen és lépésenként bemutat. Számítható ily módon a teherbírási modulus, ágyazási tényező, CBR% hagyományosan, valamint sok új jellemző és sok egyéb átszámítás. Ezek között legfontosabb a statikus tömörségi fok meghatározása, mely felterhelésenként meghatározható.
Az összehasonlító és verifikációs mérések eredményeit bemutatva azt tapasztaltuk, hogy a teherbírási modulusok ezzel a módszerrel pontosabban határozhatók meg, és a statikus tömörségi fok is alkalmasnak tűnik a további fejlesztések folytatására.
Összefoglalva, jelen publikációban célunk a statikus tárcsás tömörség- és teherbírás mérés problémáinak megoldására javasolt új műszer és egy új mérési mód bemutatása volt, mint lehetséges megoldás a teherbírási modulusok, valamint a statikus tömörségi fok meghatározására. A teherbírási modulus számításához mindig a teljes alakváltozást kell figyelembe venni, míg a tömörségi foknál csak a tömörödési alakváltozást.
Fontos az eredmények ismételhetősége szempontjából a felterhelési és kivárási idő egységesítése, az alakváltozási sebesség. Ennek megvalósítása csak a humán faktor kizárásával lehetséges. Kizárólag az automatizált mérésben látjuk a megoldást, ami teljesen kiküszöböli a szubjektív hibákat.
Ez nagy lépés lenne a párhuzamos teherbírás mérések szabványosítására is, mely most az MSZ 2509-3-ban nincs előírva. Az automatizált mérés lehetővé tenné, hogy a mérési eredményben kizárólag a talaj adottságok domináljanak és ne a mérőszemélyzet szokása. A felterhelés rögzített sebessége mellett a fix kivárás tűnik számunkra megvalósítandónak a valóban jellemző teherbírási értékek mérésének biztosításához. Ez a prototípus tesztelésekor pontosítható. A megvalósításra javasolt új statikus tömörség mérési módszer és műszer prototípus mind a teherbírási modulusok, mind a statikus tárcsás mérésből számított statikus tárcsás tömörségi fok jelenleg egyedülálló mérési módszere igen nagy segítség lenne az építőipari szakmának az egész világon, a minőségbiztosításban és a minősítésben egyaránt. Keressük ehhez Magyar partnereinket, és szponzorokat.
Az emberi hibáktól mentes automatizált mérés kiemelkedő lehet a QC/QA méréseknél. Jelenleg a minősítő teherbírás mérés a személyzettől és szokásoktól oly mértékben függ, hogy az automatizált mérés hatalmas változást és ily módon minőségi ugrást jelent az építőiparnak.
A tapasztalatok alapján a hazai MSZ2509-3 statikus teherbírás mérést is vélhetően aktualizálni lehet. Ebben segítség a prototípus kialakításának felvázolt módja, de nyilván szükségesek lesznek a nagyszámú verifikációs mérések független személyzettel, melyből a végső kialakítás és következtetés levonható. A bemutatott elmélet, a kísérleti mérések bíztatóak és indokolttá teszik a fejlesztés folytatását, kibővítését.
A következő cikkben elemezni fogjuk a tömörségi fok meghatározásához szükséges tömöríthetőségi vizsgálatotok lehetőségeit, egyszerűsítéseit, összefüggéseit, számítástechnikai alkalmazását, eddigi elemzéseket. Remélhetőleg ezek hozzájárulnak majd ahhoz, hogy egyszerűbben elvégezhetők, gyorsak és pontosak legyenek. Indokolt lehet továbbá áttekinteni a jelenlegi teherbírási előírásainkat is a megállapítások tükrében, lehet-e, kell-e változtatni valamit, milyen megoldások alkalmazhatók az eddigi problémák új megoldására, megközelítésére.
Irodalomjegyzék
[1]: Kézdi, Á. 1975: Talajmechanika II. TK Budapest
[2]: e-UT 06.03.53: Kötőanyag nélküli és hidraulikus kötőanyagú burkolatok
[3]: BS 1377- 9 [BS EN ISO 22476-3] Methods for test for soils for civil engineering purposes In-situ tests, 4.1. Determination of the vertical deformation and strength characteristics of soil by the plate loading test
[4]: MSZ 2509-3:1989 Útpályaszerkezetek teherbíró képességének vizsgálata. Tárcsás vizsgálat
[5]: MSZ EN 13286 – 2 Unbound and hydraulically bound mixtures. Part 2: Test methods for the determination of the laboratory reference density and water content. Proctor compaction.
[6]: MSZ EN 13286 – 3 Unbound and hydraulically bound mixtures. Part 3: Test methods for laboratory reference density and water content. Vibrocompression with controlled parameters.
[7]: EN 13286 – 4 Unbound and hydraulically bound mixtures. Part 4: Test methods for laboratory reference density and water content. Vibrating hammer.
[8]: Tamás, J. MK Miskolc: E kettő (E2): ember és a tévedés (kézirat / mail)
[9]: J. Hothan, H. Beyer 1993: Der Platendruckversuch im Spigel seiner Ergebnisse. Straβe und Autobahn 12 p725 – 727
[10]: Tilmann, D. 1981: Grubbs – Type Estimators for Reproducibility Variances in an Interlaboratory Test Study. Journal of Quality Technology, Volume 23, p 324 – 335]
[11]: Liptay, A. 2009: A tárcsás teherbíró képesség vizsgálatának pontossága. A mérési bizonytalanság meghatározásának problémái, ÚTLAB.
[12]: Schubert, I. & Subert A. 2023: Tárcsás teherbírás-mérés megújítása, kiegészítése, 1. rész: Tárcsás teherbírás mérés módszereinek áttekintése és kérdései, Útügyi Lapok, https://doi.org/10.36246/UL.2023.1.03
[13]: Subert I. 2005: A dinamikus tömörség- és teherbírásmérés újabb paraméterei és a modulusok átszámíthatósági kérdései, Közúti és mélyépítési szemle 55. évf. 1. sz.
[14]: Ézsiás, L. 2009: Földművizsgálati módszerek megbízhatóságának elemzése, Közlekedésépítési szemle, 59.évf. 2.szám, p.15-23.
[15]: MSZ EN 13286 – 2 Unbound and hydraulically bound mixtures. Part 2: Test methods for the determination of the laboratory reference density and water content. Proctor compaction.
[16]: Measuring Method for Dynamic Compactness & Bearing Capacity with SP-LFWD CWA 15846, WS33
[17]: Subert et al. 2017: Test and Method is Proposed for Measuring The Dynamic Compaction-rate and Dynamic Modulus in Earthworks/ „Test et méthode sont proposés pour mesurer le taux de compression dynamique et le module dynamique dans les travaux de terrassement” Proceedings of the 19th International Conference on Soil Mechanics and Geotechnical Engineering, Seoul 2017. p:657-660
[18]: Subert, I. 2006: Method for measuring Compactness-rate with New Dynamic LFWD. XIII. Danube-European Conference on Geotechnical Engineering Ljubljana, Slovenia, 2006
[19]: P02 00715 Eljárás szemcsés anyagrétegek tömörségének helyszíni mérésére
[20]: P20 00170 Javított tulajdonságú terhelőtárcsa ejtősúlyos mérőkészülékekhez
[21]: P22 00258 Előtéttárcsa terhelőtárcsás ejtősúlyos mérőkészülékekhez
[22]: P23 00011 Készülék és eljárás talajok és szemcsés anyagok fizikai jellemzőinek, különösen statikus tömörségének meghatározásához
[23]: FGSV 516:2003 Merkblatt für die Verdichtung das Untergrundes mit Unterbaues im Straßenbau.
[24]: CWA 15846 Measuring Method for Dynamic Compactness & Bearing Capacity with SP-LFWD, WS33
[25]: Subert, I. 2006: Dynamical compactibility measurements on Hungarian highways and reconstruction in cities, Geotechnical Conference in Ráckeve, Hungary (17-18. of October 2006.)
[26]: Subert, I. 2005: Dinamikus tömörségmérés aktuális kérdései. A dinamikus tömörség mérés újabb tapasztalatai, Geotechnika Konferencia, Ráckeve. (2005. október 18-20.)
[27]: Subert, I. 2004: Új, környezetkímélő, gazdaságos mérőeszközök a közlekedésépítésben, Geotechnika Konferencia, Ráckeve. (2004. okt. 26-27.)
[28]: Subert, I. 2005: A dinamikus tömörség- és teherbírásmérés újabb paraméterei és a modulusok átszámíthatósági kérdései, Közúti és mélyépítési szemle 55. évf. 1. sz.
Erre a szövegre így hivatkozhat:
Schubert István és Subert András: Tárcsás teherbírás-mérés megújítása, kiegészítése, 2. rész Statikus tárcsás méréssel meghatározott tömörségi fok, 2023, DOI: 10.36246/UL.2023.2.06
