https://doi.org/10.36246/UL.2023.1.03
2023; 11. évfolyam, 17. szám
Bevezetés
A világ egyik legrégebbi és legismertebb terepi mérési módszere a „Load-Plate Test” statikus tárcsás teherbírás vizsgálat, avagy tárcsás teherbírás mérés. Az USA-ban a terhelőtárcsa vastagsága 1.0 inch, azaz 25,4mm és átmérőjük 152-762mm közötti (6-30 in. 6-os lépcsővel). Európában jellemzően a 12 inch-es (≈30cm) tárcsaméret alkalmazása terjedt el. A nemzetközi és hazai szabványok tanulmányozásakor felismertük, hogy a terhelés sebessége, kivárások szabályai döntőek. A szabványokban párhuzamos vizsgálatra nincs előírás, a mérésre nincs ismételhetőség. A mérési eredmények jelentősen eltérőek lehetnek.
Magyarországon a statikus tárcsás vizsgálatot az MSZ 2509-3:1989 [2] szabályozza. A terhelés két ciklusos, talajoknál 0,3 N/mm2, míg pályaszerkezeti rétegnél 0,5 N/mm2 (MPa) kell legyen a felterhelési ciklus vége.
A tárcsás vizsgálatot végző személyzettől függően a mérések közötti eltérés igen nagy lehet a teherbírási modulusban. A felterhelések közötti kivárás (≤0,02mm/perc alakváltozás befejeződött-e vagy sem) megítélése szubjektív. A mérőeszköz jellemzően tárcsából és terhelő hidraulikából, valamint a terhelés ellensúlyához csatlakozó kitámasztó-szerkezetből áll. A tárcsa süllyedését 0,01mm pontos alakváltozás mérővel biztosítják. A tárcsa alakváltozását elhanyagoljuk és merevnek feltételezzük.
Probléma a mérés végrehajtásakor, hogy azt földközelben, kellemetlen testhelyzetben, a terhelő ellensúly (gép) alatt, kell elvégezni. Ez fárasztó, nyomasztó és veszélyes is. A vizsgálat ugyanakkor igen elterjedt, ismert és elfogadott, azaz mértékadónak tekintett sok helyen a világban, így hazánkban is. A teherbírás a kivitelezett szerkezet minősítő méréseinek egyike, magas és mélyépítésben egyaránt. A másik fontos minősítési paraméter a tömörségi fok.
Teherbírási szabványok áttekintése és kivonatos ismertetésük
MSZ 2509-3:1989 Útpályaszerkezetek teherbíró képességének vizsgálata
Az első felterhelésnél a mérést Δp=0,05 N/mm2 lépcsőkkel, a másodikat gyorsabban, Δp=0,1 N/mm2 lépcsőkkel terheljük 6 illetve 3 lépcsőben. A felterhelés lépcsőiben rögzíteni kell a mért alakváltozást 0,01mm pontossággal. A tárcsáról az alakváltozást 3 pontról, vagy a tárcsa középpontjáról kell átvenni. A „kivárás” a mérőóra leolvasása előtt szabályozott. A szabvány 4.2. pontja szerint az egyes terhelési lépcsők akkor tekinthetők befejezettnek, ha a mérőórák által jelzett elmozdulás 0,02 mm/perc-nél már nem nagyobb sebességű (≤0,02mm/perc). Ez a mérést természetesen nagymértékben lelassítja – ha betartják. A mérőórán leolvasva egy osztás/30sec ez minimális kivárás pontonként. Ez a felállás utáni 6 mérési pont, majd visszaterhelés két lépcsőben, majd felterhelés újabb felterhelés 3 lépcsővel, mindösszesen 6+2+3=11 pontot, azaz mindösszesen minimum 5,5 perc a kivárási idő – a terhelésekhez szükséges idő nélkül – összesen.
A keletkező behajlási teknő miatt a mérőóra tartó keret rögzítési pontja a terepen nem lehet közelebb 1,2 m-nél a terhelt tárcsához. A terhelő gépjármű kereke vagy gép letámasztása (pl. hengerpalást) sem lehet közelebb a tárcsa szélétől, mint 0,7 méter, ami a mért felületet terhelné.
A visszaterhelés után a maradó alakváltozás leolvasását, számítását csak az F3. függelék – mérési jkv minta tartalmazza és csak az első felterhelés után. Teherbírási modulust a terhelés p=0 és a végterhelés határa között (p=0,3MPa – talajok, vagy 0,5MPa- alsó pályaszerkezeti réteg) kell meghatározni, lineáris közelítéssel ábrázolva, a végleolvasást alkalmazva. A számítás az órákról leolvasott alakváltozási érték alapján történik.
A készülék / mérőeszköz követelményei: terhelő gépkocsi, trailer, munkagép min 2,4m legyen a szabad keréktávolsággal a 300mm-es tárcsa szélétől mérve. Három mérőórát kell alkalmazni (120°-ban elhelyezve), vagy egyet a tárcsa közepét mérve. A hidraulikus terhelő berendezés kalibrált mérőórával kell mérjen. A 300mm átmérőjű terhelőtárcsa minimum 20mm vastag kell legyen. A mérőóra leolvasás 0,01mm pontosságú és min 10mm mérési határú. Az órák feltámasztása a mérő-állvány lába 2,4m-re lehet a tárcsa szélétől, vagy Benkelman-tartót kell alkalmazni, a tárcsa közepére helyezve a tapintócsúcsot.
Mérési eljárás a következő: homokterítés, majd tárcsa elhelyezése, terhelőberendezés és mérőórák rögzítése szükséges. Előterhelés 0,02 N/mm2, majd, ha s≤0,02mm/min, akkor kell megszüntetni az előterhelést, nullázni az órákat és elkezdeni a mérést. A terhelési lépcsők az első felterheléskor 0,05 MPa lépcsőben 6db 0,3 MPa-ig. A leolvasás előtti kivárás szükséges addig, amíg az alakváltozás 0,02mm/min nem lesz lépcsőnként. p=0,5 Mpa a terhelési határ, ha a réteg nem talaj, hanem pályaszerkezeti réteg. A visszaterhelés két lépcsőben történik, majd újabb felterhelést kell alkalmazni dupla, 0,1MPa terhelési lépcsőben, de ennek visszaterhelése már nem szabályozott.
Az ágyazási együttható maghatározásához az 1,25mm-hez tartozó terhelést is le kell olvasni mérés során majd ebből kell számolni a “C” ágyazási együtthatót (N/mm3). A szabvány a teherbírási modulus számítására a Boussinesq-féle képletet alkalmazza azzal, hogy a Poisson (haránt-kontrakciós tényező) szemcsés anyagnál 0,3, míg agyagnál 0,5 kell legyen. A Boussinesq-féle tárcsaszorzó értékét π/2-re kell választani [1]. A szabvány az F3 mellékletben megadott „egyszerűsített képletben” viszont c=2 Boussinesq tárcsaszorzó és m=0,5 Poisson tényező mellett a c∙(1-µ2)=1,5 közelítő érték felvételét megengedhetőnek, alkalmazhatónak tünteti fel. A mérés eredménye az E1 és E2 valamint a “C” ágyazási együttható (N/mm3) értéke.
Ismételhetőségi és precizitási előírás nincs. A mérés pontosságára a szabvány 4.4.4. pontjában egy eredményre az egy tizedes pontosságot adja meg és sem a párhuzamos, sem az ismétlési vizsgálatokra, azok megengedett eltérésére, az ismételhetőségre nem ad iránymutatást.
A szabvány a terhelési sebességet nem szabályozza. A mérési hőmérséklet mérésére és a mért réteg víztartalmának mérésére nincs előírás. Azt kell mondjuk, hogy a megismert mérési szabványok között elhelyezve kiemelkedően praktikus, a megengedett határok között egyszerűnek nevezhető, jól kidolgozott mérési szabványt alkottak elődjeink (dr. Gáspár László és dr. Boromisza Tibor) 1989-ben.
DIN 18134 „Baugrund – Versuche und Versuchsgeräte – Plattendruckversuch
(DIN 18134 „Soil – Testing procedures and testing equipment – Plate load test, English translation of DIN 18134:2012-04 translation by DIN-Sprachendienst)
A tárcsaméret 300/ 600/ 762 mm lehet. Az ellensúly min 10 kN-nal nagyobb legyen, mint a méréshez szükséges maximális terhelés igénye. A tárcsa vastagsága d=300mm-nél minimum 25mm legyen, és középen a kiképzett tapintó üregben legyen a tárcsa közepének süllyedése mérhető. Terhelő berendezés 0,01 MN/m2 felbontású a d=300mm tárcsánál. Mérési hőmérséklet 0-40°C között megengedett. Víztartalom mérésre előírás nincs, de a felület takarása (árnyékolása) ajánlott.
Alakváltozásmérő követelményei: kialakítási követelmény van a mérésre 0,3m mélyen is, az alakváltozás tartomány 10mm, mérési pontosság ≤0,04mm, felbontás min 0,01mm. Távolság a tárcsaközép és a terhelő gépjármű /gép kereke között >0,75m legyen.
Előterhelés: 30sec 0,01 MN/m2 terheléssel. Mérés: első ciklus (Strain modulusból számított Evi), első felterhelés min 6, közel egyenletes lépcsőben, visszaterhelés három lépcsőben (50-25-2%). Pihentetés 120sec (útszerkezetnél 30sec) kell legyen. A második ciklus terhelése első lépcsőig (preultimate-stage-ig) történik.
Az alakváltozást kiszámolják a mérőkar áttétele alapján, majd számolják az Ev modulust az első és a második terhelési ciklusra. A számítás másodfokú regressziós analízisből megállapított egyenlet alapján történik, melyet a 0,3∙σ és 0,7∙σ közötti alakváltozás – terhelés adatok alapján számítják. (A pontosnak vélt számítás mellett a Poisson tényezőt és Boussinesq-tárcsaszorzót indifferensnek tekinti, szorzatukat 1,5-nek kell feltételezni).
Új mérés kell ez után az ágyazási tényezőhöz, a „Subgrade-reaction” Ks értékre, s = 1,25 mm-ig, melyet már a D = 762mm-es tárcsával kell mérni. Ehhez meg kell határozni felterhelési görbe inflexiós pontját harmadfokú polinommal, majd meghatározni az iránytangens alapján adódó metszéket (sp0 értéket). majd ehhez adja az s*=1,25mm értéket és határozza meg az e ponthoz tartozó p’ terhelés σ0 értékét. Ebből a ks= σ0 /s* (MN/m3).
A visszaterhelési görbe ez esetben ugyan indifferens, de a mérését előírják.
Megjegyzés: a σ0 értéke a mintapéldában 0,186 MPa, ugyanaz, mint az MSZ2509-3-ban. Függelék „A” szabályozza az erőmérő rendszer és az alakváltozás mérő rendszer kalibrációs követelményeit, melyet 10-35°C között kell elvégezni, nyolc terhelési lépcsőben 0,5 MN/m2-ig. Megengedett terhelési hiba 2% lehet. Kalibráció évente szükséges az „A” függelék szerint.
Megjegyzés: visszaterhelési zéró-kontrol a kalibrációból hiányzik.
ASTM D1194-94 Standard Test Method for Bearing Capacity of Soil for Static Load and Spread Footings
Szabványos vizsgálati módszer talajok és szórt alapok teherbírására statikus terheléssel.
A készülékre vonatkozó előírás: a hidraulika legyen alkalmas 50 tonna (440kN) terhelő erő közvetítésére, ±2% terhelési tűréssel. Terhelő tárcsa vastagsága 25,4mm (1 inch), átmérője 12-30 in között lehet (6 in. lépcsőkkel). A süllyedés mérési pontossága legalább 0,25 mm (0,1 in) kell legyen. A mérési módot és helyét a „supervising engineer” határozza meg és vezeti le (NOTE 1).
A szabványos mérési eljárás szabályozza a mérési terület kiválasztását, a teszt helyét, a megtisztítandó mérési hely mélységét, a terület szükséges méretét (zavartalan talajfelület szükséges). Az ellensúlyok támasztógerendára helyezett platformra kerülnek 1 tona/ft2 elhelyezésben. A terhelési ciklusok között legalább 15 perc pihentetési időt kell hagyni. A mérés végrehajtásához – ha megfelelő terhelhetőség biztosítható – a tárcsa átmérő 10%-ának megfelelő alakváltozás eléréséig kell folytatni.
Egy másik módszerrel (NOTE 5) minden terhelési lépcső után a leolvasásokat 30s-1-2-4-8-15min időpontokban kell elvégezni. A 6. pontban „Precision and Bias” cím alatt óvatosságra int a szabvány a mérési megbízhatóság és ismételhetőség tekintetében (lásd mint ASTM D1195) és kéri a módszert felhasználókat arra, hogy tájékoztassák az erre vonatkozó tapasztalatokról a „subcomittee”-t.
A szabványban megadottak alapján általunk becsült egy méréshez szükséges idő körülbelül három órát tesz ki.
Bias and Precision –a következő megjegyzés áll a földmű-, az alapozás-, illetve a szemcsés útalapok teherbírás minősítésére használatos mérésre:
6.1. The precision and bias of this test method for determining the bearing capacity of soil in place by means of a field loading test has not been determined. No available methods provide absolute values for the bearing capacity of soil in place against which this method can be compared. The variability of the soil and the resulting disturbance of the soil under the loading plate do not allow for the repetitive duplication of test results required to obtain a meaningful statistical evaluation. The subcommittee is seeking pertinent data from users of this method which may be used to develop meaningful statements of precision and bias.
„6.1. Ennek a vizsgálati módszernek a pontosságát és megbízhatóságát a talaj teherbíró képességének terepi terhelési vizsgálattal történő meghatározására vonatkozóan nem határozták meg. Egyetlen rendelkezésre álló módszer sem biztosít olyan abszolút értékeket a talaj teherbíró képességére vonatkozóan, amelyekkel ez a módszer összehasonlítható lenne. A talaj változékonysága és az ebből eredő zavarok a terhelőtárcsa alatt mért eredményekben nem teszi lehetővé az ismételt vizsgálati eredmény megkettőzését, ami az érdemi statisztikai értékeléshez szükséges. Az albizottság e módszer felhasználóitól olyan releváns adatokat keres, amely felhasználható a pontosságra és megbízhatóságára vonatkozó jelentős megállapítások kidolgozására.”
ASTM D1195/D1195M-21 Standard Test Method for Repetitive Static Plate Test of Soils and Flexible pavement Components for Use in Evaluation and Design of Airport and Highway Pavements
Szabványos vizsgálati módszer a talajok és hajlékony pályaszerkezeti rétegek ismétlődő statikus tárcsás vizsgálatának értékeléséhez és repülőtéri és autópálya-burkolatok tervezéséhez.
3.1.4. “rebound deflection” visszaalakulási alakváltozás, amikor a terhelés megszűnik és 3.1.5. “residual deflection” maradó alakváltozás, különbség a felterhelés és terhelés megszüntetés okozta maradó alakváltozásban egy vagy több terhelési lépcsőnél. Feszültség – strain modulus tekintetében a terhelés 0,3∙σ és 0,7∙σ közötti szakaszát kell értékelni.
Készülék / mérőeszköz követelmények: terhelő gépkocsi, trailer, munkagép min 2,4m szabad keréktávolsággal, hidraulikus terhelő berendezés, kalibrált mérőórával. Terhelőtárcsa 1 in. 25,4mm vastag, Átmérő 152-762 mm közötti (6-30 in. 6 in. lépcsővel). A mérőórák előírása 0,02mm pontosság, a 600-762mm-es tárcsáknál 0,01mm. Mérőgerenda az órák tartására 5,5m és 2,4m távolságra legyen a legnagyobb tárcsa szélétől.
A tárcsákat sorrendben egymásra kell helyezni (pyramid arrangement) a méréskor a kellő teherelosztás miatt, ahol az alsó tárcsa az alkalmazott tárcsaátmérő. A 300mm átmérőjű tárcsa vastagsága 25,4 mm, a 600 vagy 762 tárcsa vastagsága 20mm (de akkor az merevítő bordával ellátott) kell legyen. A mérési hőmérséklet 0-40°C, a mérőóra karja a -0,3m mérést is lehetővé kell tegye. Mérőóra két óra, vagy három (120°-ban elhelyezve).
Mérési eljárás: homokterítés, majd tárcsa elhelyezés, terhelőberendezés és mérőórák rögzítése. Az alkalmazott 0,05Mpa előterhelés hatására az alakváltozás érje el legalább 1,0 mm-t, majd, tehermentesítés szükséges, amikor az órákat nullázni kell. Terhelés sebességét úgy kell megválasztani, hogy az alakváltozás kb. 1,0mm és utána a kivárás 0,03mm/perc (max 3 percig) állandó legyen. A visszaterhelés után a kivárási idő 3 perc. Hat felterhelési lépcsőt kell alkalmazni ezzel az eljárással. Ez után emelni kell a terhelést 5,1mm-ig ugyanezzel az eljárással, majd újra 10,2mm-ig ugyanezzel az eljárással, azaz három felterhelést kell alkalmazni. A teljes visszaterhelés után a visszaalakulásra (relaxáció) mindig 3 percet kell biztosítani. A terhelési és alakváltozási adatokat fel kell jegyezni. A hőmérsékletet félóránként kell mérni. A víztartalom mérése nincs szabályozva.
A mérési szabványt 2021-ben frissítették. Az útépítési célú mérésekre p=0,5MPa végterhelést és két felterhelési ciklust írtak elő, 0,01MPa előterheléssel, majd 6 lépcsős felterheléssel – lépcsőnként egységes 60s kivárással. Visszaterhelés az előterhelésig két lépcsőben 60-60s kivárással történik, majd a második felterhelés – egyezően az elsővel – az utolsó előtti terhelésig történik 60s kivárással a leolvasás előtt. Mind a d=300-as, mind a d=762mm-es átmérőjű mérés lépcsőit és kivárási időket táblázat megadásával szabályozták. A 0,3∙σ és 0,7∙σ között mindkét terhelési ciklusra másodfokú polinommal regressziós görbét számol, melyből az átlagos süllyedést az átlagos terheléshez a regressziós másodfokú képlet alapján újraszámítja, majd ebből számítja az Ev1 és Ev2 értékét.
A második ciklus egy terhelési lépcsővel kevesebb, mint az első, de a strain modulus számításakor az első felterhelési határt (p=0,5 MPa) kell figyelembe venni. E szabvány engedi meg először a digitális (egyéb) mérőórák alkalmazását. Függeléke tartalmazza a terhelő berendezés kalibrációját 300/600 és 762mm-es tárcsákra, nyolc terhelési lépcsővel, p=0,5MPa-ig ±2% tűréssel.
Kalibrációnál az alkalmazott alakváltozás mérésének megfelelőségét legalább öt mérési sorozattal kell igazolni a referencia eszközhöz viszonyítva. A Benkelman-tartóhoz hasonló leolvasó kart szintén kalibrálják, méreteit ellenőrizve és tanúsítva.
Ismételhetőség és precizitás – a következő megjegyzés áll a földmű-, az alapozás-, illetve a szemcsés útalapok teherbírásának minősítésére használt mérésre:
14.1. The Precision and Bias of this test method for making repetitive static plate tests on subgrade soils and flexible pavements components has not been determined. Soils and flexible pavements at the same location may exhibit significantly different load-deflection relationships. No method presently exist to evaluate the precision of a group of repetitive plate load tests on soils and flexible pavements components because of the variability of these materials. The subcommitee is seeking pertinent data from users of this test method that may be used to develop meaningful statements of precision and bias.
„14.1. Ennek a vizsgálati módszernek a pontosságát és megbízhatóságát az altalajokon és rugalmas pályaszerkezeti rétegeken végzett ismételt statikus teljes tesztek elvégzéséhez nem határozták meg. Az azonos helyen lévő talajok és rugalmas pályaszerkezetek jelentősen eltérő terhelés-behajlás viszonyokat mutathatnak. Jelenleg nem létezik módszer a talajokon és a rugalmas pályaszerkezetek- elemeken végzett ismétlődő terhelési mérések pontosságának értékelésére ezen anyagok változatossága miatt. Az albizottság e vizsgálati módszer felhasználóitól kér olyan releváns adatokat, amelyek felhasználhatók a pontosságra és megbízhatóságra vonatkozó teljes értékű megállapítások kidolgozására.”
ASTM D1196/D1196M-12 Nonrepetative Static Load Tests of Soils and Flexible Pavement Components, for Use in Evaluation and Design of Airport and Highway Pavements
A mérés altalajokra és nem kötött, vagy hidraulikus kötőanyagú alaprétegek vizsgálatára, az ágyazási tényező és a nyírószilárdság meghatározására (3.1.p) készült. Igen sokban hasonlít az előzőekben ismertetett ASTM D1195 előírásaihoz.
2.1.2. “rebound deflection” visszaalakulási alakváltozás, amikor a terhelés megszűnik, 2.1.3. “residual deflection” maradó alakváltozás, különbség a felterhelés és terhelés megszüntetés okozta maradó alakváltozásban. Egy vagy több terhelési feszültség – strain modulus számításához a terhelés 0,3∙σ és 0,7∙σ közötti szakaszát kell értékelni.
Készülék / mérőeszköz követelmények ugyan azok, mint az ASTM D1195 előírásban. A hidraulikus terhelő berendezés kalibrált mérőórával, hőmérséklet mérését is előírja (5.6.p). A terhelőtárcsa 1 inch azaz 25,4 mm vastag és 152-762mm átmérő közöttiek (6-30 in. 6 in. lépcsővel). Mérőóra kettő, vagy több, 0,01 mm pontossággal. 600-762 mm-es tárcsáknál, max. 25mm behajlás mérésére. Mérőgerenda feltámasztása 5,5m az órák tartására és 2,4m távolság legyen a legnagyobb tárcsa szélétől.
A tárcsákat sorrendben egymásra kell helyezni (pyramid arrangement) a méréskor a kellő teherelosztás miatt, az alsó tárcsa az alkalmazott tárcsaátmérő. valamennyi tárcsa vastagsága 25,4 mm.
Mérési eljárás: homokterítés, majd tárcsa elhelyezés, terhelőberendezés és mérőórák rögzítése. A mérési terület környékét letakarással védi a száradástól, naptól.
A mérést előterheléssel kell kezdeni, ami 0,25-0,51mm alakváltozást okoz, majd kivárás szükséges. Ha az alakváltozás megáll, az órákat lenullázza. A mérést 6 lépcsőben terheli fel az első ciklusban úgy, hogy a kivárás lépcsőnként 0,03 mm/min alakváltozás-mentes kell legyen. A mérést addig kell folyatni amíg a terhelési kapacitása a hidraulikának ki nem merül, vagy a kiválasztott behajlást el nem érik. Visszaterhelés utáni kivárás 0,03 mm/3min. A terhelési és alakváltozási adatokat rögzíti. A tárcsa mellett kell mérni a hőmérsékletet fél óránként.
A számítások és terhelés-alakváltozás görbe ábrázolása előtt korrekciót végez, ami a zéró óraállításhoz tartozó behajlást és figyelembe veszi (megadja) a terhelés teljes terheléshez viszonyított arányait, a visszaalakulási és maradó alakváltozás értékét. Víztartalom mérése nincs szabályozva.
Ismételhetőségre és precizitásra – annak hiányára vonatkozó figyelemfelhívás a 8.pontban ugyanaz, mint azt az ASTM D1195-nél jeleztük.
BS 1377- 9 (BS EN ISO 22476-3) Methods for test for soils for civil engineering purposes In-situ tests, 4.1. Determination of the vertical deformation and strength characteristics of soil by the plate loading test
A Brit szabvány öt módszert tartalmaz a helyszíni terepi sűrűség meghatározására (tömörség meghatározásához), három módszert a behatolási ellenállás (pl PCT) meghatározására, négy módszert a függőleges alakváltozási és szilárdsági jellemzők meghatározására (CBR és PLT), valamint két módszert az in situ korróziós jellemzők meghatározására (electrical resistivity, electro-chemical potential of soil).
A teherbírás-mérési eljárás a következő:
Ki kell választani a vizsgálati helyet és a mérési mélységet azon a ponton, ahová az alapot építik. Ha a vizsgálatot próbagödörben végzik, szélessége legalább 4-5-szöröse legyen a lemez átmérőjének. Óvatosan leszedik és eltávolítják az összes laza anyagot úgy, hogy a terület a tárcsa alatt vízszintes és lehetőleg zavartalan maradjon. A tárcsát vékony réteg – 10-15 mm vastagságú (!!) – tiszta, száraz homokra helyezik, hogy egy kiegyenlítést hozzon létre a felületen. Ez után egy kis előterhelést kell alkalmazni, aminek 5 kPa-nál kisebbnek kell lennie. Ez után meghatározott, kis lépésekben végrehajtott terhelési lépcsőkkel – hidraulikus emelőt az ellensúlynak támasztva – mérnek lépcsőzetesen alakváltozást az adott terhelési ciklushoz, amíg el nem érik a maximális vizsgálati terhelést. A mérés az alakváltozás tárcsaátmérő 15%-káig, benyomódásáig ajánlott. A visszaterhelést több lépcsőben kell végrehajtani. A terhelés minden lépcsőnél leolvasásra kerül. A mérőóra leolvasási pontossága ±0,05mm. Hőmérő 0,5°C pontosságú legyen. Minimum 3 mérőórát kell elhelyezni 120°-ban a tárcsán, hogy az egész tárcsa elmozdulás mérése pontos legyen.
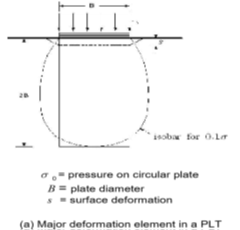
A szabvány szerint végzett mérések tapasztalatit összegző cikkek egyikéből [23] mutatunk egy ábrát, ami a valós terepi körülmények között végzett helyszíni tesztek terhelés süllyedés görbéinek jellemző és jól ismert mintáit mutatja be (1. ábra). Ezeket a későbbiekben elemezni fogjuk, mint a plasztikus, rugalmas és tömörödési alakváltozás együttes hatását, melynek arányai a vizsgált anyag típusától és állagától, víztartalmától függőek. A terhelés okozta a feszültségi zónát (p≥ 0,1σ esetén) szerzők a tárcsaátmérő kétszeresére becsülik (2.ábra).
 |
 |
Teherbírás-mérő eszközök bemutatása, következtetések
Jellemző kialakítások
A gyártott tárcsás mérőeszköz típusokra jellemző, hogy az általunk is említett valamennyi szabványos mérésre alkalmasnak jelölik a gyártók. Fontosnak tartottuk ezek értékelését, mert egy-egy jellemző megoldás leleményes és a mérést gyorsabbá teszi, vagy egyszerűen csak követendő példának tartjuk.
 |
Jellemző a prizmatikus tárcsaelhelyezés oly módon, hogy a tárcsafülek nem zavaróak. A hidraulika pumpa kézi, egyutas, terhelésmentesítése szelepes. A mérőórákhoz a javasolt tartót (zártszelvényt) alkalmazza, mérőórák száma három.
 |
d=300-as tárcsa, két alakváltozás mérő órával, hidraulika pumpa kézi, nyomásmérő óra többskálás, hidraulika egyutas, terhelésmentesítése szelepes. Felül látható ellenmenetes támasz-kiegyenlítő leleményes megoldás, a gyors távolságkiegyenlítésre alkalmas.
 |
Három alakváltozás mérő órával, hidraulika pumpa kézi, nyomásmérő óra többskálás, hidraulika egyutas, terhelésmentesítése szelepes. Felül látható rudas kitámasztás több méretben alkalmas a támasz-kiegyenlítésre.
 |
d=300-as tárcsa, három alakváltozás mérő órával, mely a tárcsára rögzített mágneses talpakra tapint. A hidraulika pumpa kézi, nyomásmérő óra egyskálás, hidraulika egyutas, terhelésmentesítése szelepes. A speciális 60°-os háromszög keretet távolabb elhelyezett lábak tartják, talajba szúrható tüskéken.
 |
Behajlásmentes mérőrúd, állíthatóan rögzülő mérőóra tartókkal, hidraulika pumpa kézi, nyomásmérő digitális kijelzéssel, bőröndben elhelyezve. Hidraulika toldás és közgyűrűk a tartozékok.
Mérési munkakörülmények
Az altalaj vizsgálata a terhelő ellensúly nélkül lehetetlen, ezért a földközeli munka és a berendezés elhelyezése négykézlábas, nehéz feladat. A mérés elején az előterheléskor újra be kell mászni a gép alá, az órákat nullázni. Ezek erősen próbára teszik a mérő személyzetet, nem beszélve a szűk helyről és a veszélyekről. A munkagépek alja jellemzően sáros, olajos, nem ideális környezetnek nevezhető.
 |
Néhány képen ezt mutatjuk be azért, hogy érthető legyen, miért is szeretnénk ezeket a mérési feltételeket kiváltani, a méréssel járó kínokat lehetőleg csökkenteni.
Észrevételek
A mérési szabványok próbálnak szigorú előírásokat alkalmazni annak érdekében, hogy a mérés megbízhatóságát és mérési pontosságát, valamint megfelelő ismételhetőségét biztosítsák, ez azonban nem mutatkozik sikeresnek. A mérések egyértelműen túlszabályozottak és szinte betarthatatlanok. Az ASTM D1195/D1195M-21 szabvány 14.1 pontjában jelzett mérési bizonytalanság okot ad az aggodalomra, egyben kötelez a mérnöki megoldásra, útkeresésre.
Néhány gondolatot ezért fel kell vessünk – a megoldáshoz vezető út keresésekor ezeket fontosnak tartjuk leszögezni. Ezek a
- a Boussinesq képletben szereplő (1-µ2)∙c szorzat „egyszerűsítése” a XXI században?
- a mérési eredményben mit jelent, milyen súlyú a Poisson tényező elhanyagolása?
- egy mérőóra, vagy három legyen?
- kell-e a tárcsára merevítő borda, vagy sem?
- a tárcsás teherbírást hogyan vonatkoztatjuk az adott alapozásra?
Boussinesq képletben szereplő (1-µ2)∙c szorzat egyszerűsítése
Szinte valamennyi mérési szabvány (ASTM, DIN és BS) alkalmazza a Boussinesq képletben szereplő (1-µ2)∙c szorzat egyszerűsítését, mellékletében még az MSZ2509-3 is, a minta-számításban. Ez azt jelenti, hogy az anyagra (talajra) jellemző „m” Poisson tényezőt figyelmen kívül hagyják. A „c” Boussinesq tárcsaszorzó merev tárcsa esetén π/2, míg hajlékony tárcsa esetén 2. Megjegyzendő, hogy Kézdi professzor erről úgy vélekedik, hogy a tárcsa inkább merev, mint hajlékony [1] Kézdi Talajmechanika II. TK.1963. Harmadik változat Ullidtz [19], illetve vélhetően ennek alkalmazásaként dr D. White is az Iowa State Universityről [20], aki a tárcsaszorzót a dinamikus LFWD-nél 8/3-ra választja szemcsés anyagoknál és 4/3-ra kohéziós talajoknál (µ=0,4 Poisson tényező mellett), ami nem π/2, sem c=2, mint azt eredetileg Boussinesq javasolta, hanem a parabola (inverz parabola) súlyponti távolsága.
Egy mérőóra, vagy három legyen?
A német szakirodalom tanulmánya szerint [25] már korábban felmerült a gyanú, hogy egy elmozdulás-mérő órával mért eredmény nem azonos a háromórás teherbírási modulus eredménnyel.
A vitát Németországban kísérleti mérésekkel tisztázták. 1993-ban Hothan és Beyer a Straβe und Autobahn folyóirat 12. számában [21] ismerteti a két mérési módszerrel mért összehasonlító vizsgálatok eredményét – mely szerint nem azonosak a mérési eredmények.
Annak érdekében, hogy a két mérés módszer összehasonlítását ne zavarja a mérés helye (altalaj) és mert közismerten nem ismételhető, azaz eltérő teherbíró képesség – egy tárcsás műszerrel mértek azonos helyen, azonos terhelési fokozatokban négy órával. Egy elmozdulás mérővel középen és három elmozdulás mérővel a szélen mérték folyamatosan a tárcsa süllyedését. Az E1 és E2 alakváltozási modulust mindegyik mérési helyen mindkét mérési eljárással egy időben mért süllyedésekből számították ki. Az eredmények kb 10%-os eltérést mutattak, csak az óra-elhelyezés miatt.
Hothan és Beyer vizsgálata csak a két eljárás által meghatározott különbségre terjedt ki és megállapították, hogy a két módszer nem ad azonos eredményt. A különbségek szignifikánsak voltak, de nagyságuk függött a mért süllyedés értékétől, a nyomóerőtől és a talaj típusától.
Az eredményekből egyértelműen megállapították, hogy egy elmozdulás-mérő órával mért süllyedések nagyobbak, mint a 3 órával mért süllyedések átlaga, vélhetően a tárcsa meghajlása miatt.
Ez igazolja a ASTM szabványokban előírt prizmatikus mérési tárcsa-kialakítás indokoltságát, vagy azokat a különleges tárcsakialakításokat, melyek bordával merevítettek. Következtetésként levonható ajánlás, hogy a tárcsaközépen végzett mérést kell megvalósítani, ha az lehetséges.
Tilmann Deutler és Hans Haas [22] 1996-ban a fenti mérési értékek felhasználásával tovább folytatta az eredmények értékelését és meghatározták mindkét módszer szerinti tárcsás teherbírás mérés relatív szórásának mérésével a jellemző és meglehetősen gyenge – mérési pontosságot is, jelezte összefoglaló ÚTLAB tanulmányában Liptay [25] 2009-ben.
Kell-e a tárcsára merevítő borda, vagy sem?
Ez a kérdés egyértelműen a d≥300mm-nél nagyobb átmérőjű tárcsáknál merült fel korábban. Amióta azonban kiderült, hogy a középen mért egy órás, illetve a három órás mérések között ekkora a különbség, azóta tudjuk, hogy indokolt lehet még a d=300mm-es tárcsa bordás merevítése is. Ennek hátránya csupán annyi, hogy a fém tárcsák amúgy is magas súlyát duplájára növeli.
Az ASTM-ben megszokott módon a merevítő bordás tárcsák nem helyezhetők egymásra, azaz a piramikus hatás nem érhető el.
A tárcsás teherbírást hogyan vonatkoztatjuk az adott alapozásra?
A terhelést azonosnak tekintve [23], a 0,1σ feszültség zóna kialakulása a terhelt sáv szélességétől függ, a hatásmélység különböző irodalmak szerint 1,5-2,0-szerese az terhelési átmérőnek. A létrejövő süllyedés a tárcsás mérésben mért süllyedésből számítható. Ezért a tárcsás mérés egy fontos mérés ahhoz, hogy az alapozás megfelelőségét el lehessen bírálni.
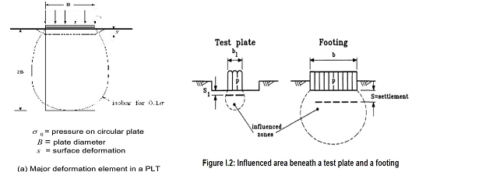
Therzaghi and Peck (1967) kohéziós talajokra [24] javasolt képlete (1) ahol f (footing), p (plate)
\[ s_f =\ \frac{B_f}{B_p} \]
\[ s_f=\left[\frac{B_f\left(B_p+0,3\right)}{B_p\left(B_f+0,3\right)}\right]^2 \]
 |
Mit jelent, milyen súlyú a Poisson tényező elhanyagolása?
Ha a Poisson tényező 0,3 (szemcsés anyag) és a „c” Boussinesq tárcsaszorzót merev tárcsának választjuk, akkor ez 1,43 azaz a „szabványosan 1,5-tel” számolt teherbírási modulus 95%-ka.
Ha a Poisson tényező 0,4 (nálunk átmeneti talaj pl. iszapos homok) és a „c” Boussinesq tárcsaszorzót merev tárcsának választjuk, akkor ez 1,32 (azaz 1,32/1,5=0,86), azaz a „szabványosan” számolt modulus 86%-ka.
Ha a Poisson tényezőt 0,5 (folyadékként viselkedő plasztikus anyag például plasztikus agyag) és a „c” Boussinesq tárcsaszorzót merev tárcsának választjuk, akkor ez 1,12 (azaz 1,12/1,5=0,79), azaz a „szabványosan” számolt modulus 79%-ka. Ullidtz – White álltal javasolt szorzó a szemcsés anyagnál számolt modulus 149%, míg kohéziós talajoknál 99%-ra adódik. Megjegyzendő, hogy mindez még mindig nem magyarázza azt, hogy egy méteren belül miért nem tudunk két hasonló mérési eredményt produkálni – egy homogénnek tekinthető rétegen.
Az Ei (i=1-2) teherbírási modulust a Boussinesq-féle képletből kell számtani, a tárcsaszorzó és a Poisson-tényező ismeretében. A magyar előírásban is szerepel a „közelítő képletet” az „egyszerűbb” számításra – a Függelékben a jegyzőkönyv mintánál. (Ha ugyanis c=2 és µ=0,5 akkor a képlet akár fejben is számolható mert a c∙(1-µ2)=1,5. Ugyanakkor ez nyilván a mérési pontosság kárára nem mehet. Ráadásul a XXI században már illő pontosan számolni. Főleg, ha a valós paraméterekkel nem is egyező ez az „egyszerűsítés”. A c=2 Boussinesq szerint a hajlékony tárcsa szorzója, a µ=0,5 pedig az agyag Poisson-tényezője. Mi ebben az egyszerűsítés? A merev tárcsa Boussinesq szorzója az MSZ 2509-3 szerint is π/2. A szabvány a Poisson-tényezőre 0,3 (szemcsés), vagy 0,5 értéket (kötött anyag) ad meg. Az átmeneti talajoknál (főleg iszapos talajoknál siSa) hazánkban is el kezdett terjedni a 0,4 érték Poisson tényező alkalmazása is, melyet semmiképp nem lehet ellenezni.
Az, hogy a „c” Boussinesq-féle tárcsa szorzóra és a Poisson tényezőre mit választunk (mi az anyag és mi a tárcsaszorzó), alapvetően megváltoztatja a mért teherbírás értékét, azaz nem elhanyagolható, nem egyszerűsíthető. Jól mutatja ezt az 1.sz táblázat összefoglalója (ha az alakváltozás 1,00 mm, akkor ezek az értékek a számított E2 MPa teherbírás értékei). Azonos alakváltozás ellenére, a számítási mód megválasztása tehát döntő lehet!
| Cµ=konstans értékek, ha c=2 hajlékony tárcsa | µ=0,3 | µ=0,4 | µ=0,5 |
| p=0,3 MPa | 81,9 | 75,6 | 67,5 |
| p=0,5 MPa | 136,5 | 126 | 112,5 |
| Ei=Cµ/s | |||
| Cµ=konstans értékek, ha c=π/2 merev tárcsa | µ=0,3 | µ=0,4 | µ=0,5 |
| p=0,3 MPa | 64,3 | 59,4 | 53,0 |
| p=0,5 MPa | 107,2 | 99,0 | 88,4 |
Az „egyszerűsített” képletben Cµ értéke 1,5∙p∙r=67,5 (p=0,3MPa esetén), mely nem tekinthető elfogadható helyettesítésnek ma már. Ez persze nagyban függ az adott mérési szabványtól is, melyek a leolvasási pontokat is, az E2 számításának módját is rögzítik. Sajnos az említett MSZ2509-3 az F.3.-ban megadott jegyzőkönyv mintában is az egyszerűsített képlet szerepel (mint a gyakorlat számára általában megfelelő egyszerűsített képlettel) de azzal is számol! Pedig a magyar szabvány 4.4.2. pontjában megadott képlet egyértelmű:
\[ E_2 =\ \frac{\pi}{2}\bullet\frac{\left(1-\mu^2\right)p\bullet r}{s_2} \]
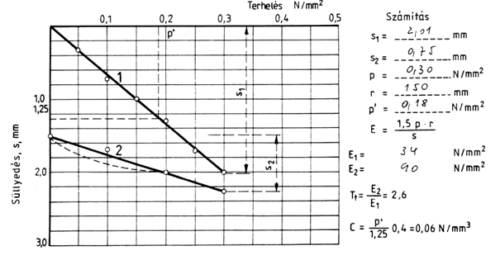
A teherbírás mérésre jellemző terhelés – minta alakváltozási görbe a következő a F3 szerint (lásd 10. ábra).
 |
Különböző nemzetközi szabványok más-más megfontolásokat alkalmaznak, hogy a terhelési-alakváltozási görbének mely pontjait tekintik alkalmasnak arra, hogy abból az első, vagy második felterheléshez tartozó teherbírási modulust számítsák, mennyi ideig tartson egy terhelési ponton való kivárás, ezen belül hány leolvasás történjen és még sok más szempont mind-mind eltérő módon szabályozott. Az „egyszerűsítés” (c=2 és µ=0,5) a legtöbb külföldi szabályozásban megjelenik.
 |
Információ a magyar teherbírás mérésből jellemzően csak a terheléshez tartozó alakváltozás, a két felterhelési lépcsőben. A végtelen, homogén féltérre jellemző mérési paramétereket – így a teherbírást is – feltételekkel illik kezelni. A mért teherbírás – a Δp terhelési lépcsőkkel – ellensúlyt igénylő mérés. A közvetlenül, vagy közvetve mért paraméter kettő vagy egy tizedes pontossággal kerül általában megadásra. Párhuzamos mérést a teherbírási modulus mérésekor mi sem alkalmazunk.
A mért alakváltozás – általában 0,01mm pontosságú mérőórával, vagy digitális mérővel történik. Egy műszert találtunk ami részben „automatizált”, de az alakváltozás időbeni kivárása itt sincs kellően szabályozva, az pedig jelentősen befolyásolhatja az eredményt.
Hatásmélység
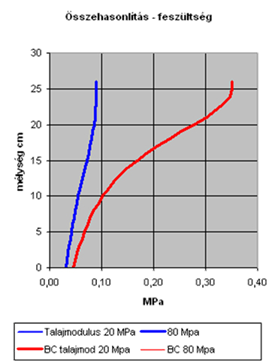
A hatásmélység Boussinesq-féle feszültségeloszlásból számítható is [1], és általában a p=20%, vagy az alakváltozás 10% elérésekor húzzuk meg (különböző szakirodalmak eltérhetnek). Számításaink szerint p=0,3MPa terhelésnél és d=300mm tárcsaátmérőnél ez 265 mm-re jött ki E2=80MPa-nál, azaz kb 30cm-nek vehető, de a hatásmélység mindig számítható (11 ábra). Ebből az következik, hogy a méréssel jellemezhető réteg hatékony vastagsága nem pont 1,5-2D. A dinamikus mérőeszköznél például a 0,1MPa tárcsa alatti terhelésű D300-as tárcsa és a 0,3MPa tárcsa alatti terhelésű D163mm átmérőjű tárcsa hatásmélysége közel egyenlő ugyan de változó, azaz nem csak az átmérő, hanem a tárcsa alatti terhelés is fontos (11. ábra).
 |
Más források is 1,5-2,0D hatásmélységet jeleznek. Elemzésünk Kézdi professzor [1] szerinti számításból azt mutatta, hogy nem mindegy a tárcsa alatti terhelés sem, és nem csak a tárcsa átmérőt kell figyelembe venni.
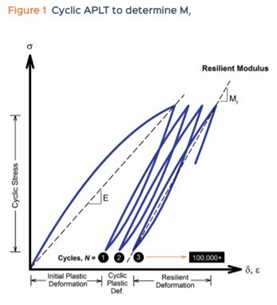
APLT Automata Plate Load Test (Anix GmbH) módszer elmélete
Az Automata Plate Load Test (Anix GmbH) elméletében a különlegesség az, hogy három felterhelést végez és a harmadik ciklus alakváltozásából meghatározza a Mr reziliens modulust (12.ábra), azt feltételezve, hogy már tisztán rugalmas az alakváltozás a harmadik ciklusban. Plasztikus alakváltozást azonban ez az elmélet sem mér, a rugalmasnak tekintett alakváltozást is kétségekkel fogadjuk. Véleményünk szerint minden elméletnek figyelembe kellene venni, azaz mérni a plasztikus alakváltozást, mert a nélkül nem lehet a tisztán rugalmas alakváltozást meghatározni.
 |
EUROCOD-7
Geotechnikai tervezés itt idézett pontja alatt a következő – általános – számítási lehetőséget biztosítja, melyet ezért illik ismertetni, de újdonságot már nem tartalmaz:

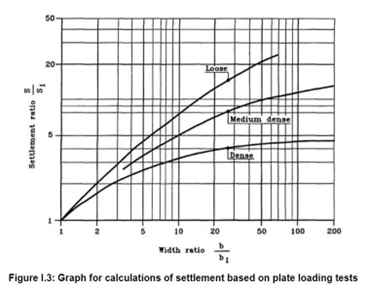
Fontos felismerni, hogy a statikus mérési adatok a mérés hatásmélységének ismeretében, hogyan adaptálhatók az alapozásra, laza, közepes sűrűségű és tömör altalaj esetén.
Itt a hatásmélységet a 13.sz. ábra a tárcsa átmérő 1,5-szörösében adja meg, a bevont „talajgömb” nyomási határát pedig a feszültség 20%-ánál javasolja megszabni. A tömörségre vonatkozóan laza, közepesen tömör, illetve tömör fogalmakat használ. Nyilvánvaló, hogy a terhelés hatására a mért süllyedések ettől erősen függőek. Az ábra azért is érdekes, mert a mért talajzóna homogén, míg az alapozás alatti talajzóna már nem biztos, hogy az.
 |
Tárcsás összehasonlító mérésből levonható következtetések, hiba-analízis
2008-ban végrehajtott hazai statikus és dinamikus méréseket elemez cikkében Ézsiás [26]. A földművek megfelelőségének igazolása két fő paraméter, a tömörségi fok és a teherbírási modulus meghatározásával történik. Az UTLAB szövetség keretében 2008 tavaszán az éppen épülő M6 autópályán készült egy összehasonlító vizsgálatsorozat a Közlekedéstudományi Intézet és a Magyar Közút Kht lebonyolításában. A cél egyrészt a kontroll (MK) és kivitelezői laborok közötti összehasonlítás, másrészt az átszámíthatóságok (statikus – dinamikus, illetve tömörségi fok) ellenőrzése volt. Az izotópos és dinamikus tömörségméréseket 4x4m-en kijelölt területen, míg a statikus és dinamikus tárcsás méréseket 12-14m szakaszokon végeztek a jelentkező akkreditált laboratóriumok. A területek homogén szakaszoknak tűntek. A mérést elvégezve, a terhelő gépkocsi 1-2 métert haladt előre, majd az újabb laboratórium mért. A kiválasztás szempontja volt az akkreditáltságon kívül a nagy gyakorlat és nagy projektekben való részvételek voltak.
A statisztikai értékelésben – ahol lehetett – a minimum, maximum értékeket kihagyta és ilymódon „korrigált” paramétereket határozott meg szerző. Statikus teherbírás mérést MSZ 2509-3:1989 módszerrel 9 labor mérte 3-3 mérési ponton, meghatározva E1, E2 és Tt értékeket.
A statisztikai számítást a Student-féle eloszlással megismételtük, hogy az egységes értékeléshez alkalmassá tegyük a statisztikát. A meghatározott E1 és a Tt értékeket terjedelmi okokból itt nem értékeljük. A cikk alábbi 2. táblázatában közölteket feldolgozva a korrigált eredményekkel való számítás mellett szerző az E2 értékekre a következő mérési megbízhatóságot állapítja meg.
MSZ2509-3 Teherbírás E2 mérések ismételhetőségi megbízhatósága (2008)
| Mérési eredmény E2 | I. szakasz | II.szakasz | III.szakasz |
| Labor száma db | 9 (7) | 9 (7) | 9 (7) |
| MIN (MPa) | 52,1 | 22,1 | 60,0 |
| MAX (MPa) | 78,5 | 63,8 | 82,7 |
| Korr. átlag (MPa) | 65,2 | 47,1 | 75,4 |
| Korr. szórás | 8,4 | 9,6 | 7,2 |
| Rel. szórás % | 13% | 20% | 10% |
| SZÁMÍTOTT (Új) ±D (Student=1,943, α=0,1 és n=n-1) | ± 9,5% | ± 14,7% | ± 7,3% |
A fentiek szerint az E2 teherbírás-mérés megbízhatósága akár ±15% is lehet (átlagosan kb ±11% volt) a korrigálások (min-max elhagyása) ellenére.
Megjegyzendő, hogy minősítéskor legálisan a min-max értékek természetesen nem hagyhatók el. Szerző megjegyzi továbbá, hogy a teljes mérési idő két felterheléssel 1,5 perctől 14 percig terjedt – azaz a mérési idő eltérése laboronként igen jelentős volt (ugyanakkor az eredményekből ez egyértelműen NEM tűnt ki).
Tárcsás vizsgálat hibáinak feltárása a mérés megújításához
Részletes hiba-analízis
Nem kerülhető el ezek után a részletes hiba analízis, mert a mérési eredmények nagy problémákat jeleznek a reprezentativitásban, a mérés ismételhetőségében. Első ezek kiküszöbölése kellene legyen, mielőtt a statikus tárcsás mérés továbbfejlesztésére, vagy a statikus tömörség mérésre bármilyen kísérletet tennénk. A hibák okát meg kell próbáljuk kideríteni. Sajnálatos, hogy ezzel kapcsolatosan alig találtunk szakirodalmat, kivéve [23], melynek címe is sokat mondó: Plate Load Test – Getting it Right. Ez pont a mérőórák (terhelés, alakváltozás) leolvasásait jelöli meg elsődleges hibaként.
A cikk elején áttekintett szabványos tárcsás mérési módszerekből, valamint az ismert magyar gyakorlatból megpróbáltunk egy hibalehetőségi mátrixot felállítani, mérlegelve, azt hogy mely pontok lehetnek lényegesek az ismételhetőségi probléma elkerülésében. Melyek azok a paraméterek, amik a talaj-jellemzőktől függetlenül rontják a mérés pontosságát, hatással vannak a mérési eljárásra, eredményére. Átnéztük, elemeztük hát a műszert, az eljárási módszert és az emberi faktort is.
A műszer elemeinek, elhelyezésének hibalehetőségei:
- acéltárcsát a terhelőgép alatt kuporogva kell emelgetni, vízszintesen elhelyezni
- ASTM előírások tárcsa-prizma kialakítása még megterhelőbb
- ASTM és DIN tárcsák vastagsága többnyire 25,4mm, a magyar előírás csak ≥20mm
- tapintó mérőórát elhelyezése után, majd az előterhelést követve nullázni is kell, azaz be kell újra mászni hozzá
A mérési módszerek, eljárások rendjéről általánosságban elmondható, hogy mindegyik nagyon túlszabályozott. Olyan előírásokat kérnek, ami igen nehezen tanulható meg és igazán nehéz betartani. Túl sok a követelmény. Terhelési lépcsők a ciklustól függően változnak, figyelni kell az időt, a kivárásnál az alakváltozást adott sec alatt, aztán leolvasni három órát egyszerre, az adatokat feljegyezve, és még a terhelést is tartani… Szóval kevés keze nőtt ehhez a laboránsnak.
Megállapíthatjuk: a mérés tele van a humán hibák lehetőségeivel
- kézi pumpálás – egyenetlen a nyomás, a terhelés lüktető
- megálláskor – ha esik a nyomás megengedjük a rányomást, hosszabbítva a terhelési lépcső idejét és az e miatti alakváltozást
- a szabvány nem ad lehetőséget a Benkelman-karos leolvasásoknál a billenőkar „kopogtatására”, azaz a kivárási idő ezzel nem rövidíthető
- visszaterhelés, a nyomáscsökkentés szeleppel történik, annak sebessége ezért változó
- Egyáltalán nincs szó arról, hogy a felterhelés is, meg a vissza-terhelés is adott egyenletes sebességgel kellene történjen. Terhelési sebességről nincs szó a szabványokban
- a mérés azonnal a teljes alakváltozást akarja méri minden mérési szabványban a konszolidációval együtt, holott azt mérhetné külön is (pl későbbi ciklusban, nagyobb pontossággal)
- minden szabvány eltérő, egyben azonban egyeznek – nem egy egyszerű mérés a Plate Load Test, ezért mindig a legrutinosabb laborosokra bízzák
Mérési eredmények számítása
- a magyar szabvány helyesen alkalmazza a Poisson-tényezőt és a c=π/2 merev tárcsaszorzót
- ugyanakkor a közelítő képletben már az 1,5-ös helyettesítést megengedi az F3 mellékletben, a mintapéldában (1-µ2)∙c képletrészre
- a képletek alkalmazásának az eredmény gyenge ismételhetőségére nincs hatása, azt a mérésben kell keresni
- a magyar szabvány két felterhelést ír elő, de a második felterhelés utáni, maradó alakváltozás leolvasását már nem írja elő (pedig adódik, csak le kéne olvasni). Kár érte, elveszett adat.
Mérőórák száma és elhelyezésük
Irodalmi adatokból láttuk, hogy nem mindegy a mérőórák elhelyezése. Más eredményt ad a tárcsaközépre helyezett órával történt mérés, mint a 120° elhelyezett három órás mérés. [21]. Az eltérés 10% körüli, azaz más hibákkal is terhelt kell legyen a mérés, ha mérhetünk kétszer akkora teherbírást is egy méteren belül (lásd MIN-MAX). Ez a hiba pedig a humán faktor.
Összefoglalás
Vizsgálataink célja a tárcsás teherbírás szabályozási kérdéseinek, a mérés problémáinak mélyebb megismerése, elemzése, problémák felderítése volt a lehetséges megoldások felméréséhez, a mérés módosításának kidolgozásához, továbbfejlesztéséhez.
A legfontosabb azonban annak vizsgálata, hogy hogyan lehetséges a statikus tárcsás mérés módosításával ismételhető teherbírási eredményeket elérni, továbbá egy új módszerrel netán a statikus tömörségi fokot is meghatározni. Ehhez át kellett tekinteni az eddigi szabályozásokat, alkalmazásokat, elképzeléseket, a tömöríthetőségi vizsgálatokat, alkalmazott jellemzőket és hiba-analízist végezni, melyeket bemutattunk.
Áttekintettük a tárcsás mérési szabványokat, miben hasonlóak és miben térnek el. A világ egyik legismertebb terepi mérési módszere a „Plate Load Test” statikus tárcsás teherbírás vizsgálat, avagy tárcsás teherbírás mérés. Hasonlóságuk ellenére a szabványok igen sok eltérést rejtenek, és a megvalósíthatóságban a humán faktor bizonyult a legnagyobb hibalehetőségnek!
Ugyanazt a mérést is mindenki egy kicsit másképp végzi el, sőt ugyanazt az eredményt ugyanaz a mérőszemélyzet sem tudja soha megismételni – legjobb szándéka mellett sem. A mérési munkakörülmények rendkívül rosszak, fárasztóak. A nehéz tárcsák elhelyezése, a felállás a méréshez kimerítő feladat.
Ki kell jelenteni emiatt, hogy a mérés automatizálása az egyetlen hatékony megoldás. Az amerikai, brit és német szabványok szerint is lehetetlen a párhuzamos vizsgálat bevezetése, a mérés ismételhetősége gyenge. Ez mellbevágó, mert a teherbírás mérés fontos minősítő vizsgálat. Igazi mérnöki feladat az, hogy a megbízhatóságát fokozzuk és az ismételhetőséget biztosítsuk.
Áttekintettük a mérési eszközök kialakításait, milyen előnyöket és hátrányokat mutatnak, miben térnek el. A mérések előkészítése, a műszer felállításának feladata nehéz és sok időt vesz igénybe a terepen, egyszerűsítése ezért indokolt lenne. Később ezeknek a tapasztalatoknak nagy szerepe lehet az automata műszer kialakításában.
Észrevételeztük a Boussinesq képletben szereplő (1-µ2)∙c szorzat „egyszerűsítését”, a Poisson tényező elhanyagolását, egy mérőóra, vagy három kérdését, a merevítő bordák szükségességét, a hatásmélységet. Ézsiás 2008 évi feldolgozása szerint az E2 teherbírás-mérés megbízhatósága akár ±15% is lehet, a korrigálások (min-max értékek elhagyása) ellenére!!! A min-max értékek nagyon nagy eltéréseket mutattak.
Elvégeztük végül a magyar tárcsás vizsgálat hibáinak feltárását a mérés megújításához. A részletes hiba-analízis a mérési eredményekben nagy problémákat jelzett a reprezentativitásban, a mérés ismételhetőségében. Első feladat ezek kiküszöbölése kellene legyen. A műszer, a mérés elemeinek, elhelyezésének hibalehetőségeit vizsgálva megállapítottuk, hogy a mérési módszerek, eljárások rendje mindegyik túlszabályozott. Olyan előírásokat adnak, ami igen nehezen tanulható és igazán nehéz betartani. Túl sok a követelmény.
Megállapíthattuk, hogy a mérés tele van a humán hibák lehetőségeivel. A terhelési sebességről nincs szó a szabványokban. Keverednek az alakváltozások, nem különböztethető meg a rugalmas, a maradó – ezen belül pedig a plasztikus és a tömörödés miatti alakváltozás. A mérési eredmények számítása hibás, mert (1-µ2)∙c nem 1,5. A mérőórák száma és elhelyezésük fontos, nem ugyanazt az alakváltozást adják – azaz a tárcsa behajlása kimutathatóan más középen, mint a széleken mérve.
Véleményünk szerint minden teherbírás mérési elméletnek figyelembe kellene venni a plasztikus és a tömörödési alakváltozást, mert a nélkül nem lehet a tisztán rugalmas alakváltozást meghatározni. A teljes alakváltozás rugalmas és maradó alakváltozásból áll, de a maradó alakváltozás két részre osztódik, a plasztikus és tömörödési alakváltozásra.
Összefoglalva tehát megállapíthattuk, hogy a humán személyzet okozta hibák elkerülhetetlenek, a legjobb szándék mellett sem küszöbölhetők ki – ez okozza a teherbírás mérés alapvető problémáit. Felmerül ezért megoldásként az automatikus mérés kidolgozása, a humán beavatkozás nélküli automata mérőműszer szükségessége, mint egyetlen járható út a párhuzamos mérések biztosítására, a programozhatóságra, a megfelelő ismételhetőség lehetőségének megteremtésére – akár a mesterséges intelligencia, az AI- előkészítéseként értelmezve.
Jelen tanulmányunkban leírt szabványos módszerek mindegyikével megismételhetetlen a teherbírási modulus mért eredménye. Ennek oka elsősorban az, hogy a terhelési sebesség nem konstans, hogy a kivárási idő változó, hogy a lépcsőnkénti kivárások alatti alakváltozás egyenként sem ismételhető. Hat (három) lépcső alkalmazása során ezek az alakváltozások nem ismételhető módon szuperponálódnak. Kijelenthető, hogy nem a személyzet képzettsége vagy gyakorlata dönt az ismételhetetlenség mellett, hanem egyszerűen önmagában a humán faktor. Ha jót akar, akkor is rányom a hidraulika pumpára, ha azt látja, hogy a hidraulika nyomása esésnek indul. Ezek kiküszöbölése csak XXI. századi mérési módszerekkel, processzoros vezérléssel lehet megvalósítható.
A probléma lényege tehát az, hogy már az első felterheléskor is a mért alakváltozásban nem határolható be sem a plasztikus alakváltozási rész, sem a rugalmas alakváltozás valamint a levegő eltávozása miatti statikus tömörödési alakváltozás – de még ezek aránya is változó. Ezek a felterhelési ciklusokban is arányaiban változnak, azaz nem azonosíthatók az első, vagy második felterhelésből sem. Mindez anyagfüggő és víztartalom függő is.
Hiba-analízisünk kimutatta azt is, hogy ha ezeknek a megállapításoknak a helytállóságát elfogadjuk, akkor a terhelési ciklusokban a lépcsőnkénti kivárási időt vagy meg kell szüntetni, vagy szigorúan egységesíteni szükséges. Az adott terhelési lépcsőn az álladó nyomás (megállított felterhelés) mellett mért alakváltozás változik, a mérőórán látott kúszás pedig tény. A visszaterheléskor történő leolvasásokat semmire sem használják, feleslegesek. Csak a relaxáció miatt alkalmazzák. Ugyanakkor ebből nem deríthető még ki az, hogy ennek milyen arányú a plasztikus-, rugalmas-, illetve tömörödési alakváltozása. A teherbírási modulusban a teljes alakváltozást vesszük figyelembe, de nincs annak akadálya, hogy még több terhelési ciklussal tisztázzuk az alakváltozások anyagra, talajra, víztartalomra jellemző paramétereit, összetevőit.
Fentiek alapján megállapíthatjuk, hogy a jelenlegi teherbírás mérés sajnos valóban nem kellően ismételhető és valóban nem elegendő megbízhatóságú. Ugyanakkor a teherbírás E2 (MPa) minősítő mérés, az ezzel járó joghatással, ezért a hibák minél nagyobb mértékű kiküszöbölésére kell törekedjünk – ráadásul sürgősséggel.
Szakirodalmi Jegyzék
[1]: Kézdi, Á. 1975: Talajmechanika II. TK Budapest.
[2]: MSZ 2509-3:1989: Útpályaszerkezetek teherbíró képességének vizsgálata. Tárcsás vizsgálat.
[3]: DIN 18134 „Baugrund – Versuche und Versuchsgeräte – Plattendruckversuch.
[4]: DIN 18134 „Soil – Testing procedures and testing equipment – Plate load test, Engish translation of DIN 18134:2012-04 translation by DIN-Sprachendienst.
[5]: ASTM D1194-94 Standard Test Method for Bearing Capacity of Soil for Static Load and Spread Footings.
[6]: ASTM D1195/D1195M-21. Standard Test Method for Repetititive Static Plate Test of Soils and Flexible pavement Components for Use in Eveluation and Design of Airport and Highway Pevements.
[7]: ASTM D1196/D1196M-12. Nonrepetative Static Load Tests of Soils and Flexible Pavement Components, for Use in Evaluation and Design of Airport and Highway Pavements.
[8]: ASTM D 1196 – 93: Reapproved 1997. Standard Test Method for Non-Repetitive Static Plate Load Tests of Soils and Flexible Pavement Components, for Use in Evaluation and Design of Airport and Highway Pavements, ASTM, US.
[9]: AASHTO T 222-81. 2021: Standard Method of Test for Nonrepetitive Static Plate Load Test of Soils and Flexible Pavement Components for Use in Evaluation and Design of Airport and Highway Pavements.
[10]: AASHTO (1981). AASHTO T 222 – 94, Standard Method of Test for Non-Repetitive Static Plate Load. Test of Soils and Flexible Pavement Components, for Use in Evaluation and Design of Airport and Highway Pavements, American Association of State Highways and Transport Officials.
[11]: EN1977-1 Eurocode 7 – Geotechnikai tervezés – 1.rész: Általános szabályok.
[12]: EN1977-2 Eurocode 7 – Geotechnical design – Part 2: Ground investigation and testing plate load tests, field vane tests and penne ability tests)
[13]: BS 1377- 9 (BS EN ISO 22476-3) Methods for test for soils for civil engineering purposes In-situ tests, 4.1. Determination of the vertical deformation and strength characteristics of soil by the plate loading test.
[14]: ÖNORM B 4417 – Geotechnik – Untersuchung von Böden – Statischer Lastplattenversuch / ÖNORM B 4417 – Geotechnika – Talajok vizsgálata – Statikus terhelőlemez vizsgálat.
[15]: TSC 06.720: 2003: Meritve in preiskave – Deformacijski moduli vgrajenih materialov, Republika Slovenija.
[16]: NF P94-117-1: 2000-04, Portance des plates formes – Module sous chargement statique à la plaque, Norme française (France).
[17]: Standard UNE 103808:2006 15.2.2006 – Load test of plate soils
[18]: CRD-C655-95 Standard Test Method for Determining the Modulus of Soil Reaction
[19]: Ullidtz, P. 1987: Pavement Analysis. Elsevier. Developments in civil Engineering, 19
[20]: White D.J. 2013: Stiffness-Based_QC-QA Testing Tech Brief. Central Iowa Pavement Test Sections.
[21]: Hothan, J., Beyer, H. 1993: Der Platendruckversuch im Spigel seiner Ergebnisse. Straβe und Autobahn 1993./12 p725 – 727.
[22]: Deutler T. 1991: Grubbs-Type Estimators for Reproducibility Variances in an Interlaboratory Test Study. Journal of Quality Technology, Volume 23, p 324 – 335)
[23]: Anyang, M. Y., Atarigiya, B. D., Ofori-Addo, R. & Allotey, N. K. 2018: Plate Load Test: Getting it Right. GHIE th50 Engineering GHANA’s Sustainable Development.
[24]: Terzaghi, K, Peck, R. B., Mesri, G. 1967: Soil Mechanics in Engineering Practice, 2nd Ed., John Wiley & Sons, Inc.
[25]: Liptay, A. 2009: A tárcsás teherbíró képesség vizsgálatának pontossága. A mérési bizonytalanság meghatározásának problémái /ÚTLAB 2009.
[26]: Ézsiás, L. 2009: Földművizsgálati módszerek megbízhatóságának elemzése, Közlekedésépítési szemle, 59.évf. 2.szám, p.15-23.
[27]: Gáspár, L., Károly, R., Boromisza, T. 2008: Útpályaszerkezetek teherbírása hazai és külföldi eredmények és problémák. Közúti és Mélyépítési Szemle (6) p.:1-8
[28]: Boromisza, T. 1997: Útpályaszerkezetek teherbírásmérése és az értékelés jelenlegi hazai gyakorlata. Közúti Közl. és Mélyépítési Szemle, 1997/3 p.:142-144.
[29]: Boromisza, T. 1968: A talaj rugalmasságának vizsgálata útpályaszerkezeteknél Mélyépítéstudományi Szemle, (6).
[30]: Gáspár, L., Boromisza, T. 1963: Útpályaszerkezetek mértezése új hazai eljárással a behajlásmérés és egyenértékszámok alapján. Mélyépítéstudományi Szemle (10).
Erre a szövegre így hivatkozhat:
Schubert István és Subert András: Tárcsás teherbírás-mérés megújítása, kiegészítése, 1. rész: Tárcsás teherbírás mérés módszereinek áttekintése és kérdései, 2023, DOI: 10.36246/UL.2023.1.03
