https://doi.org/10.36246/UL.2024.2.03
2024; 12. évfolyam, 20. szám
Bevezetés, földmű és pályaszerkezet
Mi a földmű?
Mindenekelőtt tisztázzuk, hogy jelen cikkben mit értünk földműnek, illetve pályaszerkezetnek.
Hazai szakmai terminológiánktól eltérve, itt földműnek a tömörített talaj felső szintje alatti, alsó határral nem rendelkező anyagot értjük, ezt láthatjuk az 1. ábrán. Fölötte kizárólag valamilyen, szabályozásokban meghatározott követelményeknek megfelelő anyagokból – építési termékből – készült rétegek vannak, ezek összességét – jelen írás keretén belül – nevezzük pályaszerkezetnek.
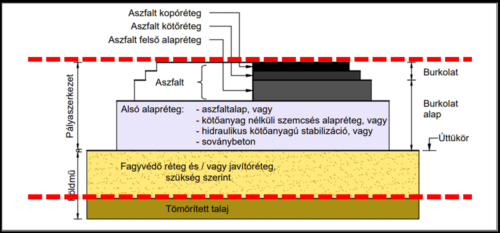 |
Ez a megközelítés a meglévő pályaszerkezetek esetében különösen hasznos, mert azok döntő részénél az ábrán látható elegáns felépítés nem található meg. Az FWD technológiát érthető módon alapvetően ezen a halmazon használják és ez az egyszerűsítés nagymértékben megkönnyíti a kiértékelést, mint a későbbiekben látni fogjuk.
A későbbiekben a pályaszerkezeten belüli rétegek vizsgálatánál ezt a leegyszerűsítést feloldjuk.
Földműtulajdonságra visszavezethető pályaszerkezet hibák
A földműnek nagyszámú tulajdonsága van, az FWD technológia oldaláról nézve ezekből két tulajdonságot említünk meg:
- merevség
A merevség a terhelés hatására bekövetkező rugalmas (nem maradó) alakváltozás mértékét mutatja meg. Alapvetően az épített és a természetes földmű merevségének nagysága biztosítja a pályaszerkezet megépíthetőségét és kellő alátámasztását.
A merevséget az FWD által létrehozott behajlásokból képesek vagyunk meghatározni.
 |
Az országos közúthálózaton végrehajtott rendszeres állapotfelvételek adataiból készült az előző ábrán látható kiértékelés.
Az eredményekhez két megjegyzés:
- A hibamennyiség elsőre meglehetősen nagynak tűnik. Kis fejszámolással, az éritett területre vetítve kiderül, hogy tizedszázalékokról van szó. A kérdésnek abban van jelentősége, hogy a szakmai és az úthasználói közvélemény nagyon érzékeny ezekre a hibákra és ennek alapján ítéli út – és földműállapotainkat rossznak és ezek a darabszámok az úthasználó számára meglehetősen jól észlelhetők.
- A másik kérdés a hibahelyek keresztirányú elhelyezkedése. Tapasztalataink szerint a hibák túlnyomó része a burkolatszél közelében található. Erre visszatérünk a későbbiekben.
- maradó alakváltozás
A szilárdságtan szigorúan értelmezve nem ismeri a maradó alakváltozásokat, a valóságban ugyanakkor ez a jelenség létezik.
Az FWD technológiával képesek vagyunk a földmű felszínén jelentkező feszültségeket számítani és – gyakorlatunk számára kellő pontossággal – olyan határértékeket megadni, amelyek korlátozzák a tervezett élettartam alatt a maradó alakváltozásokat.
 |
Tanulmányozva a 3. ábrát, láthatjuk, hogy az alapvetően aszfaltproblémának vélt keréknyomok jelentős része földmű (és/vagy szemcsés alapréteg) maradó alakváltozás (egy keresztmetszetben különböző aszfalttulajdonságú réteg aligha létezik).
A pályaszerkezet használhatósága a földműmerevség függvényében
Használhatósági kapcsolatok
A közútkezelés gyakorlatában alapvető információ a pályaszerkezet aktuális használhatósága, amit számos kritériummal lehet értelmezni.
Ezen kritériumok döntő része értelmezhető kapcsolatban van a pályaszerkezetet alátámasztó földmű merevségével.
A szakmai közvélekedés ezt jellemzően kézenfekvő ismeretként tartja számon, a szerző tapasztalata szerint ez korántsem igaz.
Néhány ilyen kapcsolat trendet a következő ábrákon tanulmányozhatunk, megjegyzendő, hogy a földműmerevségen túl valamennyi kritérium és/vagy a kapcsolat levezethető az FWD által szolgáltatott eredményekből.
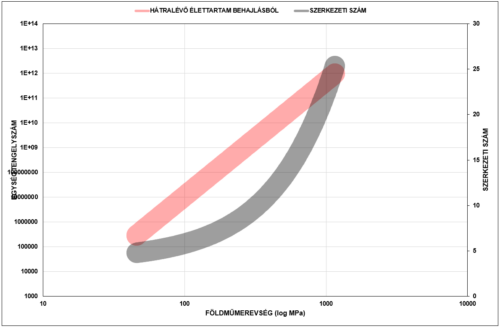
A hátralévő élettartam [1], a földműmerevség a [2], a szerkezeti szám a [3] alatti hivatkozásoknak megfelelő, megjegyzendő, hogy a szerkezeti szám a HUMU [4] által lényegében már ismert fogalom.
A kapcsolatok ábrázolása (a vastag, homályosabb vonal) az áttételek és a sztochasztika által adott bizonytalanságot akarja jelképezni.
 |
 |
Mindenesetre az ábrák a kapcsolat létét és hozzávetőleges alakját igazolják.
A szerző a fentiekkel a földmű/pálya rendszer szigorú összetartozását, a címben is kiemelt elválaszthatatlanságot kívánja hangsúlyozni, ezzel pedig az FWD által nyújtott együttes vizsgálat/értékelés lehetőségét.
Egy szellemes (Hothan – Scaefer) kiértékelési módszer
A módszer [2] grafikus kiértékelési formáját mutatom be a következő ábrán. A vízszintes tengelyen az 1200 mm – es szenzor behajlásérékéből számítható földműmerevség található (az eddigi bemutatott földműmerevségek ezzel azonos módon lettek számítva). A függőleges tengelyen a „pályaszerkezet merevség indikátor” (CBF, a központi és a 200 mm – es szenzor behajláskülönbségének a központi behajlással elosztott értéke) szerepel. Ez egyébként a 200 mm – es szenzornál értelmezhető görbülettel fordítottan arányos.
A diagramon fel van tüntetve a földmű merevség „határértéke” (az adott esetben 40 MPa) és a pályaszerkezet merevség határértéke, ami az aktuális CBF érték 0,4 hatványra emelve és egy konstanssal szorozva.
A koncepció tehát egy eljárásban vizsgálja a földműmerevség/pályaszerkezet merevség kapcsolatot, megfelelő „beállítható” határértékkel.
Vizsgáljuk meg a módszert (amelynek minden inputja az FWD mérésből származik) először egy nagyforgalmú autópályaszakaszon, amelyen a vizuális felmérések a haladósávot lényegében tönkrementnek mutatták. (a szakasz a továbbiakban még több szempontból fog szerepelni).
 |
A megjegyzések a következők:
- a módszer jól felismerhetően, határozottan megkülönbözteti a rossz állapotú haladósávot az előzősávtól, tehát kellően érzékeny
- a vizuális megjelenítés világos értékelést tesz lehetővé
- az eljárás nagyon alkalmas speciális, egyedi értékelések végrehajtására, a CBF érték nagyon könnyen alkalmazható az analitikus méretezésben is, illetve a határérték eseti körülményekhez is igazítható, ezt a későbbiekben még látni fogjuk.
Egy kisforgalmú útszakaszon végrehajtott idősoros elemzést vizsgálhatunk a következő ábrán.
 |
A következő megjegyzések tehetők:
- az ábrán 12 évnyi időterjedelem „története” látható az egyes mérési pont adatokkal és az időszaki átlagokkal
- a számítástechnika segítségével könnyűszerrel lehet az egyes adatokhoz számított valószínűségeket felvenni, amivel a szakasz állapota választott megbízhatósággal értékelhető
Természetesen itt is megvan a lehetőség, hogy más kritérium kerüljön alkalmazásra, ezáltal a pályaszerkezet gazdálkodás megalapozottabbá válhat.
Földmű részletesebben
Kis kitérő
Ez az írás az FWD technológiáról szól, de, ha azt helyesen akarjuk használni, szükség van némi talajmechanikai- meteorológiai -ismeretre.
A következő ábrán egy összefoglaló látható a földművet potenciálisan alkotó talajfajták tulajdonságairól.
 |
A táblázat a földmű osztályozása és a használat során lényeges viselkedések kapcsolatát mutatja.
A földművel kapcsolatban – nem kis mértékben a tapasztalható klimatikus változások függvényében – a következő megállapítások tehetők:
- A földmű az út leghosszabb élettartamú része. Amíg a felső rétegek a fenntartás – felújítás eseményekkel évtizedes távlatokban érdemben változnak, a földművek kiterjedt tömegei akár évszázadokon keresztül is működnek, alapvetően általunk csak korlátozottan ismert törvényszerűségek szerint.
- a meglévő utak földműállapotairól csak kivételes esetekben vannak megbízható információink, ezért is hasznosak a föld és talajvízzel kapcsolatos adatbázisok [5]
- a változékonyabbá váló klímánk mi földrajzi szélességünkön biztosan minimálisra csökkennek a fagykárok kockázatai (a szükséges tartósan alacsony hőmérsékletű időtartamok évtizedek óta nem fordulnak elő)
- az olvadási (elnedvesedési) kár valószínűleg megszűnik (évtizedek óta nincs jelentős mennyiségű, viszonylag hosszú ideig megmaradó hó)
- a viszonylag hosszú ideig tartó csapadékos periódusok (téli) esélye erősen csökken, a párolgási intenzitások várhatóan nőnek, az aktuális földmű víztartalmak várhatóan csökkennek
- a talajvízszintek tartós csökkenése várható
- a fagyveszélyes/fagyérzékeny talajfajták nagy része ugyanakkor hajlamos a térfogatváltozásra és ennek klimatikus ágensei gyors elnedvesedés – kiszáradás (főleg az aszályos periódusok veszélyesek) viszont gyakoribbak lesznek, várhatóan szaporodni fognak az ezzel kapcsolatos pályaszerkezet károk [6].
- a földműtulajdonságok a meteorológiai hatások függvényében ciklikusan rövidebb időtávon belül is változnak, ezek prognosztizálására fejlett eljárások jelentek meg a legutóbbi évtizedekben, ezek magyar nyelvű ismertetését találhatjuk [7] – [8] Az eljárás alapvetően az új pályaszerkezetek esetében hasznos.
Merevségi jellemzők, meghatározásuk
Hazai előírásaink [9] a földmű merevségét leginkább az annak tekintett réteg felületén végrehajtott, vagy az anyag laboratóriumi vizsgálat eredményével veszik azonosnak.
A valóságban ezek az eredmények leginkább a tervezési eljárásokban játszanak orientáló jellegű szerepet, a valós földműmerevségek valós körülmények között egészen más képet mutatnak.
A működő építmények esetében a földműmerevség (vessünk egy pillantást az 1. ábrára) meghatározása hagyományos, csak a felületen történő méréssel nem lehetséges. Az FWD technológia viszont erre kiválóan alkalmas.
Földműmerevség FWD készülékkel
Mindenekelőtt a legfontosabb kérdés az, hogy melyik FWD érzékelőn mért behajlást vesszük alapul a „földműmerevség” meghatározásához?
A [10] alatt számos eljárás tanulmányozható, látható, hogy a különböző műhelyek elég sokféle lehetőséget vizsgáltak.
Az 1. ábrát megnézve látható, hogy az a mélység, amitől a „földműt” értelmezzük az a konkrét felépítés függvénye.
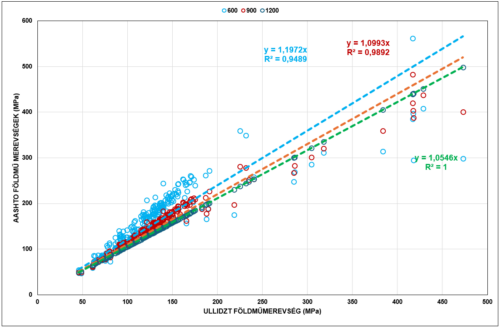 |
A 9. ábrán tanulmányozható az Ullidtz [11] által javasolt (az 1200 mm–es szenzor adataiból számítható) földműmerevség kapcsolata az AASHTO ajánlott képleteiből következő merevségértékekkel, jól látszik, hogy ebben az esetben a legszorosabb a kapcsolat, ezért is ezt az értéket használtuk, illetve használjuk.
CBR érték
A talán legrégibb, de biztosan a legelterjedtebb földmű merevségi mutató a CBR [12] amely a hazai méretezési szabályzatnak is alapja.
A mutató az USA, Kanada, Ausztrália, Dél–Afrika, Új-Zéland mellett Kínában is nagymértékben használatos.
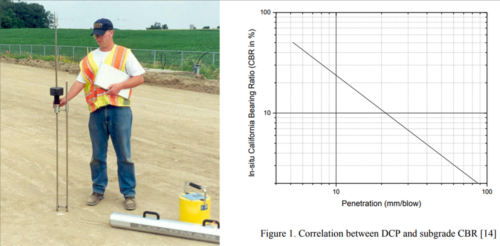
Alapvetően laborkörülmények között vált ismertté, van helyszíni meghatározási lehetősége. újabban a dinamikus kúpos verőszondával (DCP) nagyon könnyen lehet a helyszínen is meghatározni.
Külön azért érdemes kicsit foglalkozni vele, mert hatalmas mennyiségű tapasztalat és elég gyakorlatias szakirodalom áll rendelkezésre, továbbá az angolszász méretezési eljárásokban alapvető jelentősége van.
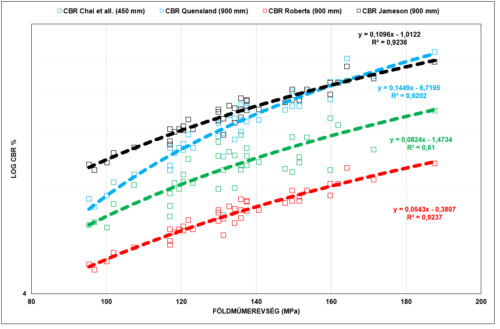
A 10. ábrán a [13] alatt ismertetett eljárás és annak összehasonlításban szereplő további módszerek eredményeit foglaltuk össze.
Valamennyi módszernél a CBR értéket a DCP kúpos verőszondával állapították meg a 9. ábra szerinti összefüggés alapján.
A földműmerevség értéket pedig FWD mérésekből határozták meg.
Jól látható, hogy az erősebb összefüggések a 900 mm – es szenzornál adódtak.
Külön felhívjuk a figyelmet, hogy a DCP szonda nagyon egyszerűen kezelhető (akár fúrólyukból is) léteznek kisgéppel üzemeltethető változatai, amelyekkel mintavétel is lehetséges, ezzel kérdéses esetekben az FWD mérésekhez nagyon értékes kiegészítések nyerhetők.
A szerző véleménye szerint célszerű lehetne a rendszeres behajlásmérések analógiájára ezzel a készülékkel aktuális földműmerevség vizsgálat és talajazonosító vizsgálat, amelyeket egy pályaszerkezet esetében (homogén szakaszon) csak egyszer kellene elvégezni, ezáltal az országos hálózaton adattárba rögzíthető értékek keletkeznének, amelyek még a felújítási döntés megalapozásához is használhatók lennének.
 |
 |
Valós földműmerevség
Vizsgáljunk meg egy – viszonylag reprezentatívnak tekinthető – halmazt a földműmerevségek változása szempontjából.
 |
Ismeretes, hogy a hazai úthálózaton az állapotfelvételi rendszerességen túl léteznek ún. etalonszakaszok [14], amelyeknek tulajdonságait tudományos alapossággal vizsgálják.
Ezen halmazból lett kiválasztva 16 főút és 12 mellékút (szakaszonként 41 mérési pont, átlagosan 10 mérési időpont).
 |
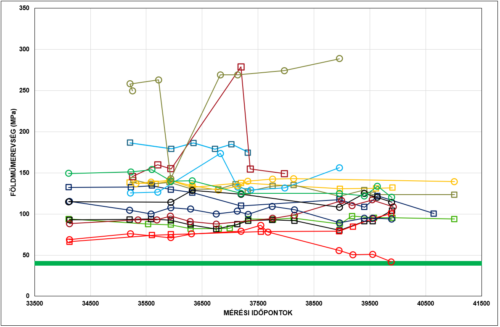
Megvizsgálva először a főutak eredményeit a következő megállapítások tehetők:
- Egyetlen mérési időpontot egy szakaszon leszámítva a földműmerevségek lényegesen nagyobbak, mint a feltüntetett, a tervezésnél használt minimumkritérium
- Meglepően szűk sávban – kis szórással – helyezkednek el az eredmények a különböző utakon
- Hosszú időtávon az eredmények meglehetősen egyenletesek
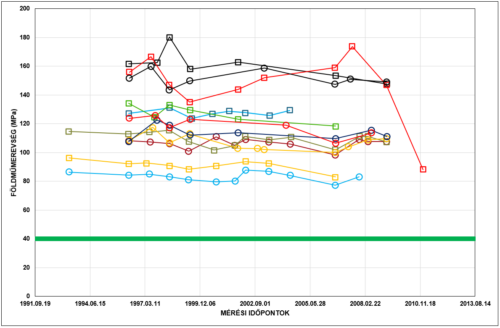
A főutak esetében tett megállapítások a mellékutak esetében is fenntarthatók.
Ezek a megállapítások nagymértékben eltérnek a szakmai közvélekedéstől (ami nem feltétlenül támaszkodik megbízható információkra) ezért a következő pontban megvizsgáljuk a kérdést.
Földmű (és pályaszerkezet) merevség keresztirányban
Az előző pontban bemutatott földműmerevségértékek szokatlan voltának több oka is van, amelyek jórészt összefüggenek a terhelésnek a tengelytől (burkolatszéltől) való távolságával.
Szilárdságtani modell kérdése
Az analitikus pályaszerkezet méretezésnél a használt számító programok döntő része vízszintes értelemben kétirányban végtelen modellt tételez.
 |
Pályaszerkezeteink ugyanakkor keresztirányban ettől érdemben eltérően viselkednek.
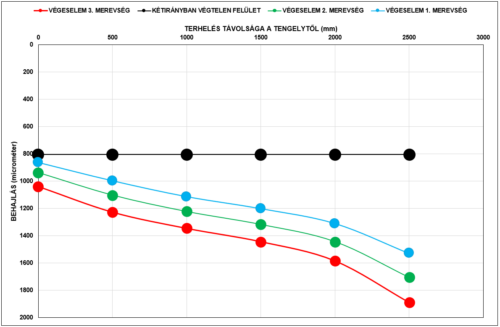
A 14. ábrán egy 6 m széles pályaszerkezet terhelés alatti behajlásai láthatók egy egyszerűbb véges elemes programmal számítva.
Jól látható, hogy a behajlások jelentősen eltérnek a kétszer végtelen modelltől és erősen függenek a pályaszerkezet merevségétől is.
Az FWD készülék a mérés során természetesen a valós viselkedéshez hasonló eredményt ad, de jól látható, hogy a mérés keresztirányú elhelyezkedése nagymértékben befolyásolja az eredményt.
Keresztirányú merevségek FWD mérésekből
Érvényes előírásunk [15] az FWD behajlásmérés keresztirányú elhelyezkedésére a következőt mondja: „Általános előírásként szolgálhat, hogy a mérést a burkolat szélétől kb. 0,8 – 1,2 méterre eső vonalban kell elvégezni.”
A hazánkban járatos FWD készülékek utánfutón helyezkednek el, ezek szélessége kb. 1700 mm., ez reálisan a burkolatszéltől 1000 mm mérési távolságot tesz lehetővé.
Tapasztalataink azt mutatják, hogy a gyakorlatban – kellően erélyes utasítás hiányában – a mérést a sáv közepén végzi a személyzet.
Vizsgáljuk meg egy, keresztirányban a tengelytől 300 – 300 mm távolságban lévő szenzorral rendelkező eszközzel végrehajtott mérés adataival a keresztirányú merevségek változását.
Három, rendre makadám, hajlékony, félmerev csoportba sorolható, 6,0 m burkolatszélességű, homogén szakaszon a D300 behajlások (átlag) értékeit, illetve ezek extrapolált értékeit tanulmányozhatjuk a 15. ábrán.
 |
Ezekből az értékekből – közelítő eljárással – lehetséges számítani a Hothan – Schaefer értékeléshez szükséges paramétereket, ezt láthatjuk a 16. ábrán.
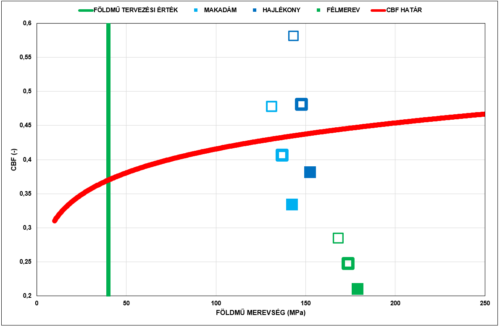 |
A következőket lehet megállapítani:
- a földműmerevségek lényegében függetlenek a burkolatszél távolságtól
- a CBF érték (pályaszerkezet – merevség indikátor) a burkolatközéptől a szél felé egyértelműen csökkenő merevséget mutat (kitöltött jelölőtől a vékonyszegélyű jelölőig)
Azaz a mérés tengelyének távolsága az úttengelytől lényeges kérdés, amit érdemi módon szabályozni kell, természetesen a mérés céljának függvényében.
Keresztirányú nedvességtartalom
Egy nagyforgalmú főúton – a felújítás után néhány évvel – a szelvény szerinti bal oldalon jelentős mennyiségű repedés keletkezett, érzékelhető deformációkkal, kátyúkkal. Az elvégzett FWD mérések alapján a következő Hothan – Schaefer kiértékelés történt.
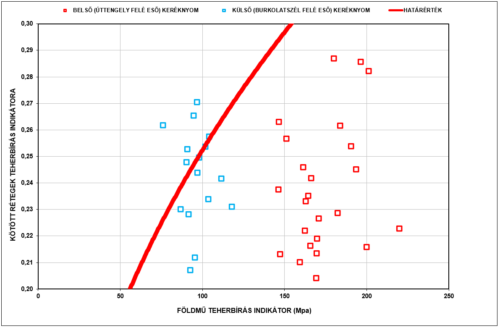 |
Jól felismerhető, hogy az azonos nagyságrendű kötött réteg indikátorok mellett a földműmerevség értékek szignifikánsan különböznek a burkolatszéltől való távolság függvényében, a külső kötött indikátorok a határértéken túl esve magyarázzák a hibákat.
A keresztirányban – burkolatbontás után – végrehajtott CBR vizsgálatok eredményét tanulmányozva a 18. ábrán egy nagyon érdekes eloszlást látunk keresztirányban.
Megállapítható, hogy a keresztszelvényben a földmű víztartalma és ezzel együtt a merevsége eltérő.
 |
Ilyen jelenségeket már viszonylag régen megfigyeltek és feljegyeztek, a jelenlegi szakmai konszenzust, a jelenség magyarázatát, továbbá a földmű víztartalomváltozások következményeinek modellezési lehetőségeit a [16] és [17] szakirodalmak tartalmazzák.
A számunkra fontos megállapítások a következők:
„A kutatók kimutatták, hogy a burkolatok alatti nedvességtartalom az építés után néhány évvel elér egy egyensúlyi állapotot. A nedvességtartalom szezonálisan még mindig ingadozhat az egyensúlyi nedvességtartalom körül. Ez az ingadozás két esetben lehet jelentős: a hideg régiókban a téli fagy és a tavaszi olvadás időszakában, valamint amikor a talajvízszint a talajfelszíntől körülbelül három lábnyira van. Ha ez a két eset valószínűtlen, mint a legtöbb esetben a száraz és félszáraz régiókban, az egyensúlyi nedvességtartalomra gyakorolt szezonális hatások jelentéktelennek tekinthetők, ha a vizsgált pont 3-6 lábra van a burkolat szélétől.”
A [18] alatt AAA. Molenaar a fenti idézethez a 19. ábrán látható képi magyarázatot fűzi.
Összefoglalva megállapítható, hogy a földmű időjárásfüggő merevségváltozása egy viszonylag jól meghatározható sávban jelentős, ami a tapasztalt viszonylag magas és kis szórású földműmerevségekre kielégítő magyarázatot ad, főleg, ha mint már említettük, tudjuk, hogy a mérések a forgalmi sáv közepén történtek.
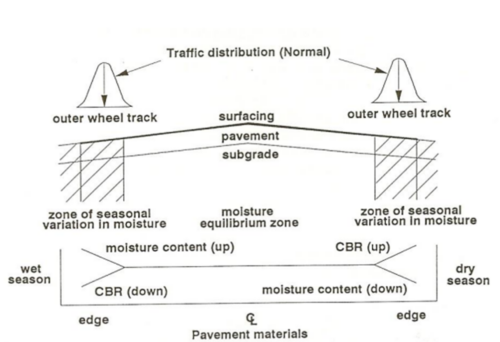 |
Ezek után csak egy kérdés marad, melyik az a meteorológiához is kapcsolható helyzet, ami a szélső sávban erősen változó, adott esetben kritikusan rossz víztartalom/földműmerevség konstellációt hozza létre.
 |
Megvizsgálva a 20. ábrát és némi tapasztalatok alapján elég határozottan állítható, hogy ez egy keresztmetszet tervezési és/vagy üzemeltetési probléma.
Föld, vagy szemcsés anyagú padkáink egyrészt vízáteresztők, másrészt hajlamosak a „felhízásra”, ezáltal a burkolatra hulló csapadék nem jut el a vízelvezető rendszerbe, hanem a földműbe beszivárogva annak merevségét csökkenti.
Itt térünk vissza az 1.2 pont alatti tapasztalt burkolathibákhoz, amelyek léte nyilvánvalóan összefüggésben van az itt ismertetett jelenséggel.
Összefoglalva a következő megállapítások tehetők:
- a pályaszerkezet jelentős része alatt a víztartalom – és ebből következően a földműmerevség – viszonylag állandónak tekinthető
- a kritikus (burkolatszéltől számítva 0,9 – 1,2 m széles sávban a nedvességtartalom változik és ebből következően a földműmerevség is
- ebben a sávban a használatos FWD készülékek nem, vagy csak korlátozottan tudnak reprezentatív módon pályaszerkezet és földműmerevséget vizsgálni
- ha ez utóbbi feltétlenül szükséges a burkolatszélnél az FWD eszközökről szóló cikkben bemutatott kézi berendezéssel, esetleg DCP szondával megállapítható a földműmerevség
- erősen megfontolandó, hogy a padka vizet át nem eresztő kivitelben készüljön el (lényegében szélesítést célszerű készíteni), mert a fenntartási gyakorlat az elnedvesedést nem tudja megakadályozni.
Földmű összenyomódás
A földmű maradó alakváltozásainak kérdése az esetek túlnyomó részében az új pályaszerkezet méretezés esetén fordul elő. A 3. ábrával kapcsolatban már említve volt, hogy a tapasztalható deformációk jelentős része nem aszfaltra vezethetők vissza és a szerző személyes tapasztalatai alapján is nagyobbnak ítéli a problémát.
Az új méretezések (ritkás) valós számításai (leggyakrabban típus – pályaszerkezeteket alkalmazunk) is általában kielégítő eredményeket mutatnak itt gyakorlatilag kizárólag mindhárom irányban végtelen szerkezetet számítunk.
A valós szerkezeti modell (lásd a 14. ábrát) ugyanakkor jóval nagyobb, a földmű felszínén értelmezhető fajlagos összenyomódást ad eredményül, így a [19] alatti munka is.
Ez a kutatás keresztirányban korlátozott méretű pályaszerkezeteket számolt véges elemes módszerrel.
Az így meghatározott, a BDI teknőparaméter függvényében számítható összenyomódások láthatók különböző pályaszerkezeteken a 21. ábrán.
Vegyük észre, hogy az új állapotú félmerev (autópálya) pályaszerkezet az egyetlen, ami a hazai érvényes összenyomódási határértéket (nem teljesen) kielégíti.
Vegyük azt is figyelembe, hogy a földműmerevségek értékei minden esetben döntően meghaladják a tervezési határértéket, azaz alapvetően kielégítő földműveken van ez az összenyomódási hiátus.
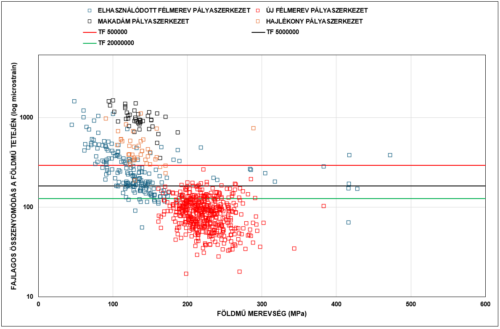 |
A kérdést itt tovább nem taglalva felhívjuk a figyelmet ezen tönkremeneteli potenciál vizsgálatának lehetőségére.
Pályaszerkezet és az FWD technológia
A pályaszerkezeteket különböző célokkal vizsgáljuk az FWD készülékkel, ezek közül a legfontosabbak a következők:
- pályaszerkezet használati tulajdonságainak meghatározása
- pályaszerkezet felújítást megelőző vizsgálatok
- minőségellenőrzési célok
Mindegyik, itt felsorolt cél megfelelő eléréséhez feltétlenül szükséges a vizsgálatok pontos meghatározása (mikor, hol, milyen gyakorisággal stb.) ami valamilyen szabályozott feltételrendszer meglétét teszi szükségessé.
Használati mérőszámok
A közutas szakma sok évtizede használ és keres egyre újabb használati mérőszámot, ami a pályaszerkezetre jellemző. A „teherbíróképességet” jellemző mérőszámokról a [20] alatt olvashatunk.
Az FWD készülék alkalmas számos a szakirodalomban felsorolt mérőszám (jellemző) mérésére.
A lehetséges használati mérőszámok közül a pályaszerkezet teherbíróképességének jellemzésére alkalmas mérőszámok közül néhány kerül bemutatásra.
Használati mérőszámok problémái
3.1.1.1. A hátralévő élettartam, mint mérőszám
Hazai gyakorlatunk a központi behajlásból számítható hátralévő élettartamot használja mérőszámként.
Vizsgáljuk meg egy nagyforgalmú meglévő autópályaszakasz számítható értékeit.
 |
Az ábrán a 6. ábrán már megismert szakaszt láthatjuk, ugyanakkor az (elvileg) levonható következtetések egészen mások, a kép egy nagyrészt még jelentős hátralévő élettartamot mutató szakaszt ábrázol.
A levonható következtetések az alábbiak:
- a szakaszon kiváló földműteherbírás tapasztalható, a központi behajlás pedig nagymértékben érzékeny erre, alacsony értéket mutat
- a Hothan/Schäfer értékelés pályaszerkezet indikátora alapvetően érzékenyebb és ennek megfelelően valósabb képet mutat, mint a behajlásból a hatványfüggvénnyel erősen túlzó élettartamot adó behajlás
- felismerhető, hogy a kapcsolat az élettartam és a földműmerevség között meglehetősen erős
Összefoglalva megállapítható, hogy alkalmazott mérőszámunk nem képes a valóságot kellően leírni, ezért célszerű lenne újat kidolgozni.
3.1.1.2. A mérési eredmények korrigálása és a homogenitás kritériuma
A [14] alatt említett, az etalonszakaszokra vonatkozó kutatás eredményei közül [21] szerint a leromlási mérőszámokról beszélve megállapítja, hogy „kivételnek a pályaszerkezet teherbírás bizonyult, amelynek idősora határozott „romló” trendet nem mutatott, hanem gyakran – beavatkozások hiányában is – „megmagyarázhatatlanul”, az egyik évről a másikra a mért értékek javultak”.
A megállapításban foglaltak valós problémák és mivel a használati mérőszámok funkciója a kellően megbízható jellemzés és előrejelzés a továbbiakban erről lesz szó.
- a pályaszerkezetek leromlásáról
A leromlási folyamatot vizsgáljuk meg először, a következő ábra segítségével.
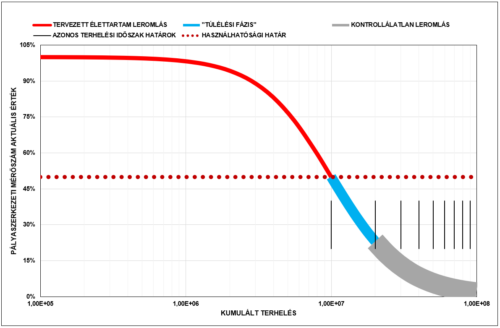 |
Az ábrán látható görbe egy fáradási függvény, amely a valóságot valamilyen matematikai eszközzel modellezi.
A valóságban a folyamatot befolyásoló tényezők (terhelés, anyagtulajdonságok, meteorológia stb.) mind csak sztochasztikusan írhatók le, ráadásul az első repedés után az érvényes szilárdságtani modell is „elveszti” determinisztikusságát, azaz a leromlás végbemenetele nagymértékben véletlenszerű eseményektől függ.
Ebből viszont következik, hogy az észlelés lehetősége is az előzőkben felsoroltak függvénye.
A valós pályaszerkezetek esetében a leromlási görbét a szerző (tapasztalatai alapján) három részre bontotta.
Az „új” állapot egy érdemi hosszúságú „változatlanságot” mutató periódus után az élettartam végéig (pl. a kötött rétegek merevségének 50% – ra való csökkenése) viszonylag jól regisztrálható változási lépcsőkkel rendelkezik, azaz érdemben megfigyelhető.
Hazai gyakorlatunkban a tervezett „élettartam” tízszeres túllépése sajnos a realitás, az első túllépési időszakot lehet „túlélési” fázisnak nevezni, amikor a véletlenszerű folyamatok az elméleti leromlással még korrelálnak, azaz a leromlás megfigyelése már rosszabb esélyekkel, de lehetséges.
Az ezután következő időszakban az események már jellemzően nincsenek kapcsolatban az elméleti leromlással, a folyamatok kontrollálatlanok.
Ez a rövid eszmefuttatás azért készült, hogy rávilágítson a megfigyelendő folyamat nagymértékű bonyolultságára és ezért a megfigyelés szabályozottságának szükségére.
Ennek a kérdésnek részletes taglalása szétfeszíti ezen írás kereteit, ezért a továbbiakban csak néhány szempont megemlítésére szorítkozunk.
- a mérés célja
Természetesen lehetséges hálózati szinten kialakítani a mérőszám változás megfigyelésének rendszerét, de ez óriási előkészítő munkát jelent.
A szerző arra lát esélyt, hogy egyes esetek kerüljenek részletes vizsgálatra, pl. egy új pályaszerkezet típus bevezetése esetén
- a mérés frekvenciája
Lényegében mindig célszerű lenne a „T0” állapot felvétele, azaz az új (felújított) állapot rögzítése. Ez egyben lehetőséget ad a teljes létesítmény homogén szakaszainak első meghatározására.
Ennek ismeretében a homogén szakaszokon meghatározható a szükséges behajlásmérések száma és a tervezett ismétlések időpontjai is (első közelítésben javasolható az évenkénti ismétlés, a későbbiekben az eredmények ismeretében ez a frekvencia csökkenthető).
- a mérés helyei
Mindenekelőtt tisztázni kell, hogy a kiválasztott mérőszámot a szakasz azonos pontjain akarjuk (kíséreljük meg) az ismételt mérésekkel meghatározni, vagy az ismérv eloszlásának változását vizsgáljuk. Mindkét eljárás lehetséges, de a mérésre vonatkozó szabályozás erősen különbözhet.
Gyakorlatunk megpróbálja az azonos ponton való mérést, de ehhez a keresztirányú mérésvonal pontos és szigorú) előírásán túl a szakasz kezdőpontjának stacionálása szükséges ezekkel jó esélyekkel megközelíthetjük az „azonos mérési pont” elvét.
- terhelés
Szigorúan meg kell határozni a terhelő erőt, ez legyen 50 kN. Az etalonszakaszok esetében előfordultak lényegesen nagyobb terhelő erők is, ráadásul egy szakaszon belül is változó módon.
Anyagaink merevsége feszültségfüggő, ez a kapcsolat jelentősen eltér a lineáristól, az átszámítások durva hibákat okozhatnak
- hőmérsékleti korrekció
A [21] alatt a kérdés elég részletesen van taglalva, egyértelmű, hogy szükség lenne hazánkban egy kellően megbízható eljárásra, illetve egy megtervezett, hosszú távú méréssorozat lehetőséget ad „helyi” korrekciós összefüggés alkalmazására és utólagos korrekciók végrehajtására.
- földmű merevség korrekció
A jól megválasztott mérőszám – a pályaszerkezetre értelmezve – elvileg független a földműmerevségtől, ugyanakkor a leromlásban a földműmerevség változása „részt vesz”.
Egyrészt a hosszabb távú megfigyelés megadja a „helyi” korrekciós összefüggés kialakítását, másrészt terhelt/terheletlen (pl. keréknyom/keréknyomok között) kétszeres mérés megadja a korrigálás „kiejtésének” lehetőségét.
 |
Befejezésül, az etalonszakaszok egyikén végrehajtott szerkezeti szám elemzés két változatát tanulmányozhatjuk, a „hagyományos” és a célirányosan korrigált és homogenizált változattal.
Felismerhető, hogy (főleg a kumulatív összeg módszer használatával) a leromlás meglehetősen kielégítő szorossággal kimutatható.
A szerkezeti szám
A szerkezeti szám (structural number) az AASHTO kísérletsorozat „terméke” és számos ország használja (többnyire erősen módosított formában) hálózatán, alapösszefüggése a következő:
\[ SN=\sum_{i=1}^{n}{a_ih_i} \]
ahol
\( S_N \) szerkezeti szám
\( a_i \) réteg együttható
\( h_i \) rétegvastagság
Az FWD technológia szempontjából érdekesebb a szerkezeti szám behajlási adatokból való meghatározásának lehetősége
A [22] és [23] hivatkozások tanulmányozása sok érdekes információ megszerzését segítheti elő, egyben megkíméli a szerzőt az alapismeretek részletezésétől.
3.1.2.1. Különböző szerkezeti számok
A [22] számos eljárást ismertet az SN meghatározására, három, kizárólag a behajlási adatokból megállapítható módszerre láthatunk példát a következő ábrán.
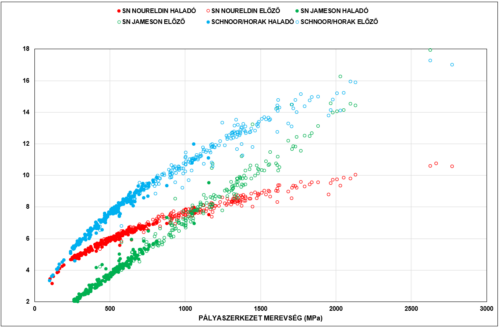 |
Jól felismerhető, hogy a különböző eljárások eredményei eltérnek, ennek számos oka van, amelyet itt nem részletezünk, de felhívja a figyelmet arra, hogy célszerű egy hálózaton egyféle eljárás alkalmazása.
A továbbiakban a Jameson eljárás eredményeit használjuk.
Megjegyzendő még, hogy a módszer fejlődése során megjelent a földmű hatását is figyelembe vevő (a behajlási adatokból szintén számítható) módosított szerkezeti szám (MSN), de ebben az írásban a pályaszerkezet kérdéseit vizsgáljuk.
3.1.2.2. Új és régi szakaszok kiértékelése
A szerkezeti szám nagyságának tervezési meghatározására a [3] tanulmányozása ad információt, megjegyzendő, hogy az ott ismertetett eljárás számos, a tervezendő/felújítandó szakasz jelentőségének függvényében meghatározható „többlet” SN érték hozzáadását is lehetővé, szükségessé teszi, amelyek a potenciális korai hibák elkerülésére ad lehetőséget.
Kifejezetten állapotértékelési célra léteznek a forgalom és a földműteherbíróképesség függvényében megadott táblázati értékek, amelyek alapján a szerző kidolgozott egy hatványfüggvényes képletet és a példák esetében ezt használta.
Tönkremeneteli határnak a meglévő pályaszerkezetek esetében az aktuális időpontban nagy (jellemzően 20 év) időszakra szükséges SN érték 60 % – át szerepeltetjük az ábrákon, ez elvileg levezethető az USA különböző államaiban alkalmazott gyakorlatból.
Vizsgáljunk meg egy új állapotú pályaszerkezetet a következő ábrán.
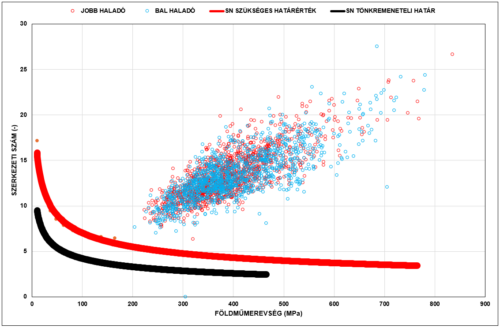 |
A következő megállapítások tehetők:
- a szerkezeti szám (Jameson képlete szerint) függetlennek tekinthető a földműmerevségtől, ez a mérőszám szempontjából fontos tulajdonság
- az új állapot minden esetben meghaladja a szükséges szerkezeti szám értéket
- az ábrázolás (ami a Hothan/Schäfer eljáráson alapszik) jól mutatja, hogy érdemi földműmerevség változások esetén is a feltételek kielégülnek
Nyilvánvaló, hogy egy útszakasz leromlásának megfigyeléséhez alapvető a T0 állapot felvétele, szerző hosszú pályafutása során többször megkísérelte ennek szabályzatban rögzítendő előírását, de ez nem volt elérhető.
Vizsgáljuk meg most a már többször szereplő nagyforgalmú autópályaszakasz állapotát.
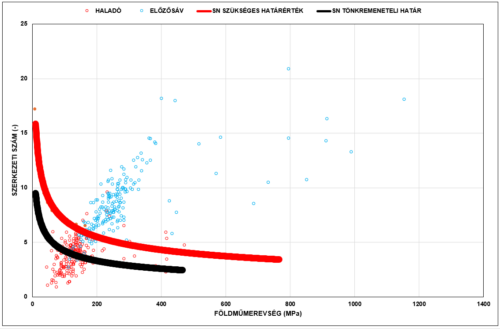 |
A megállapítások a következők:
- a szakasz, amelyen a központi behajlásból számított hátralévő élettartam megfelelőnek tűnt – lásd 22. ábra – a haladósáv tekintetében nem kielégítő, az esetek vagy felében pedig tönkrement állapotot mutatnak
- feltűnő, hogy az SN értékek elég jól korrelálnak a földműmerevséggel, aminek oka az, hogy a földműmerevség nagysága a tönkremenetelt befolyásolja, tehát a kapcsolat a leromlás során alakult ki
A két példán keresztül megállapítható, hogy a szerkezeti szám kellően érzékeny mutató és körültekintő alkalmazási eljárás esetén alkalmazása hasznos lehet.
3.1.2.3. Leromlási idősorok
A 3.1.1.2 pontban leírtak már jelezték, hogy a leromlási idősorok esetében a megfelelően informatív eredményhez sok feltételt kell teljesíteni.
A 2.3 pontban bemutatott etalonszakasz halmazon a szerző megkisérelte a szerkezeti szám leromlási folyamat megragadását.
Az eredményeket összefoglaló módon a következő ábrán lehet megvizsgálni.
A következő megállapítások tehetők:
- a leromlást csak szigorú homogenitási feltételnek megfelelő rész – szakaszon lehetett kimutatni, a teljes halmaz mintegy 15 % – ban, megjegyzendő, hogy a változás mértéke már igen csekély volt
- a leggyakoribb szituáció a tervezett élettartamot jelentősen túlélő helyzet, amikor már a szerkezet fizikailag nem képes „tovább romlani”, (a burkolat olyan állapotban van, amikor a repedezés átterjedt az összes kötött burkolatrétegre és amikor a repedéseken keresztül már nincs teherátadás) ugyanakkor a nagyon jó földműállapotok miatt még egységes.
- a szerkezeti szám megfelelő érzékenységét mutatja, hogy az egyik szakaszon az idősor vége felé hirtelen jelentősen megnőttek a számított SN értékek. A KTI publikációinak tanulmányozása után megállapítható volt, hogy a szakaszon közben egy megerősítés történt.
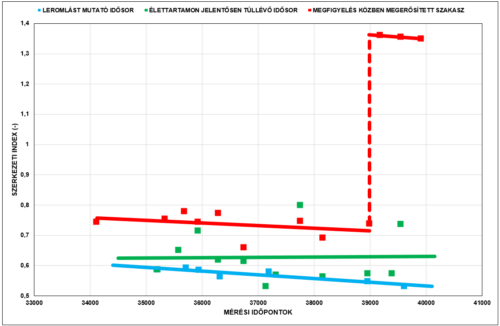 |
Összefoglalva megállapítható, hogy kellő gondosság mellett lehetséges a leromlás időbeli figyelemmel kisérése.
Egyenértékű rétegvastagság
Az egyenértékű rétegvastagság elmélet hosszú útra tekinthet vissza, egy jó összefoglaló található [24] alatt.
A hazai szakirodalomban [25] alatt található a kérdéssel foglalkozó írás.
Az egyenértékű rétegvastagság közútkezelői alkalmazásával Molenaar [26] részletesen és nagyon gyakorlatias módon foglalkozott, ezen belül a hátralévő élettartam prognosztizálására egy meglepően egyszerű, de nagyon hasznos eljárást ismertet.
Használata azon alapul, hogy mérni kell egy terhelt sávon (pl. keréknyomban) és egy terheletlen sávon (pl. keréknyomok között) a behajlási teknőt. A terheletlen sávon történő méréssel egy etalon lehetőségét kapjuk, ezáltal a fáradás jelensége megragadható.
Megjegyzendő, hogy a hazai mérési gyakorlat ezt a differencia lehetőséget a többsávos utak esetében adja meg (a nem haladó sáv forgalom által okozott terhelése jellemzően minimális).
 |
Vizsgáljuk meg a 29. ábrán egy magyar másodrendű főút négysávos szakaszán történt mérések alapján készült leromlási görbét.
A feldolgozás eredményeként a terhelt/nem terhelt mérésből származó egyenértékű rétegvastagságok szerepelnek a kumulált nehézforgalom függvényében, a piros regressziós vonal ezekből származik.
- a forgalom „0” értéke az első mérés időpontja
- az „elvi tönkremeneteli határ” értékét az eredeti (100%) érték 30 % – ban lehet felvenni (ekkor elvileg valamennyi pályaszerkezeti réteg „szemcsés anyaggá” töredezik)
- az „elvi 0 állapotot” a terhelt/nem terhelt hányados 1 értékénél lehet felvenni
- az első mérésig lefutott forgalom értéke ebből becsülhető
Jól látható, hogy a feldolgozás információtartalma lényegesen nagyobb, mint a központi behajláson alapuló módszeré.
Az eljárás hátránya az, hogy kétszer kell mérni (eredetileg a keréknyomban és a keréknyomok között) ugyanakkor ez a földmű és hőmérsékleti korrekciókból eredő hibákat kiejti, mert a nem nagy távolságban való mérésnél mind a földműállapot, mind a hőmérséklet azonosnak vehető.
Kétszer két sávos utak esetében ugyanakkor – mivel a sávonkénti mérés elvileg megtörténik – hatékonyan alkalmazható, mert a belső sávok forgalma jellemzően lényegesen kisebb.
Pályaszerkezet felújítást megelőző vizsgálatok
Az FWD technológia alapvetően a meglévő szerkezetek tulajdonságainak megállapítására szolgál, így kézenfekvő, hogy a felújításokat megelőző tervező/elemző munkában FWD lehetőségeket használjanak ki.
Érvényes hazai szabályozásunk [9] a témában meglehetősen szűkszavú, a [27] alatt tanulmányozható (hamvába holt) tervezet elég részletes előírásokat tartalmaz a potenciális FWD eredmények használatára.
Meg kell említeni elsősorban a behajlásmérési pontok számát, a korrekciós módszereket és a szabályozástervezetben szereplő teknőparaméterek kiszámítási módját, továbbá a homogén szakaszképzés módját (kumulatív összeg módszer).
Megjegyzendő még, hogy a laboratóriumi anyagvizsgálatok helyének kiválasztásánál a behajlási adatok figyelembevételét írja elő a tervezet.
Az FWD technológia a felújítások esetében a behajlásmérés alapján a felújítás tervezése szempontjából nagyon fontos eredményeket képes szolgáltatni.
Elsőként megemlítjük a meglévő pályaszerkezeti rétegek merevségének vissza – számolását az adatokból, ezzel a rétegekről szóló cikkben foglalkozunk.
A pályaszerkezeti rétegek vastagsága nagyon fontos adat lehet és ennek megbízható meghatározása roncsolásmentesen elsősorban a földradar használatával lehetséges.
Jelen cikk megírásának megkezdését megelőzően [28] alatt nagyon érdekes írás jelent meg (folytatása és hivatkozásai [29] – [31] alatt tanulmányozhatók) amely bemutatja, hogy lehetséges FWD behajlásadatokból a teljes pályaszerkezet vastagság és az aszfaltvastagság meghatározása.
Ezek az eredmények földradar vizsgálatokkal is alá lettek támasztva (lásd az idézett szakirodalmakat) és a felújítás tervezésénél a bizonytalan, vagy nem létező adattári adatok helyett nagyon hasznosak.
A hivatkozott hazai publikációban szerepelnek azok a képletek, amelyekkel a vastagságadatok meghatározhatók.
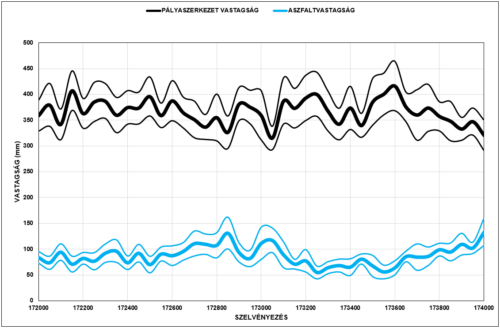 |
Megállapítható, hogy az így nyerhető vastagsági adatok jól használhatók – elsősorban a szerkezeti kialakítás (pl. szélesítés) – geometriai kialakításánál. Az aszfaltvastagság értékek hasznosak pl. a hőmérsékleti korrekciók számításánál és mint az aszfaltrétegekre vonatkozó cikkben is láthatjuk, a meglévő aszfalt merevségének vissza – számolásánál.
A felújítás során szükségessé válhat az elhasználódott aszfaltréteg részleges eltávolítása, továbbá a helyszíni újrahasznosítást előirányzó technológiák esetén szintén felmerül a kérdés, a beavatkozás után milyen felületi modulussal rendelkezik a (megmaradt) pálya.
Az említett szabályozástervezetben a problémát az Odemark eljárás átalakításával a szerző megoldotta.
Egy szakaszon bemutatjuk az eredeti és a megváltozott felületi modulusok értékeit, ezeket a következő ábrán tanulmányozhatjuk.
 |
Az ebben a pontban említett két lehetőség a felújítást tervező mérnök számára a gazdaságos és szerkezetileg a meglévő pályaszerkezettel kompatibilismegoldás kialakítását teszi lehetővé.
Minőség ellenőrzés
A minőség-ellenőrzés hazai gyakorlatában a vállalkozó saját mérései túl a megrendelő jellemzően bizonyos építési állapotokhoz köt méréseket. Ezek jellemzően egy réteg építése előtt, illetve után történnek és eredményeik elvileg döntést (eltakarás, továbbépítés) eredményeznek. Vegyük észre, hogy az eredmények nagy hányada a mérés időpontjában tekinthető reprezentatívnak, az idő múlása és a továbbépítés döntően megváltoztatja az értékeket (száradás, fellazulás, szilárdulás, leterheléshatás).
Mérési módszereink korlátai ráadásul nem teszik lehetővé, hogy a teljes szerkezet kész állapotának tulajdonságait vizsgáljuk.
Az FWD technológia, lényegénél fogva képes a teljes szerkezetre információkat adni.
Megrendelői szemmel pedig meglehetősen kézenfekvő, hogy a T0 állapotot rögzítsük, aminek előnyeit a korábbiakban már sokszor megemlítettük.
Vizsgáljuk meg egy új állapotú gyorsforgalmi út egy sávjának néhány tulajdonságát az átadást röviddel megelőző időpontban történt mérés segítségével.
Megjegyzendő, hogy a mérés nem volt a megrendelő által előírva és a vállalkozó különösebben nem örült, ami esetleg érthető, de ennek szabályozási előírása a szerző szerint fontos útgazdálkodási érdek lenne.
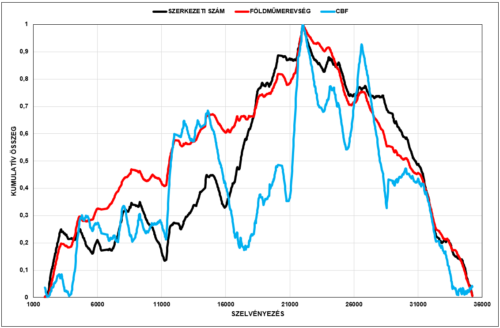 |
A 32. ábrán a forgalmi sávon mért behajlásokból számított szerkezeti szám, földműmerevség és pályaszerkezet merevség indikátor (CBF) értékek homogenitását vizsgálhatjuk.
Kellően tapasztalt elemzőnek feltűnik a görbék meglehetősen nagy irányváltásai, különösen a CBF értéké.
Megjegyzendő, hogy a forgalmi sáv szerkezeti szám értékei a 26. ábrán szerepelnek, láthatóan kellő értékkel.
Egy 2006 – ban, a Gazdasági Minisztérium megbízásából készült tanulmány [30] egy 184 elemből álló „típus” pályaszerkezet gyűjteményt állított elő, amelyben a kész pályaszerkezettel szemben a szerkezetek számításával együtt megállapított két teknőparaméter (SCI, illetve BCI) értékeit írta elő, kellő tűréssel együtt.
Ez a két érték a teljes szerkezeten belül a kötőanyagos felső rétegek, illetve az alap és javító rétegek állapotát mutatja.
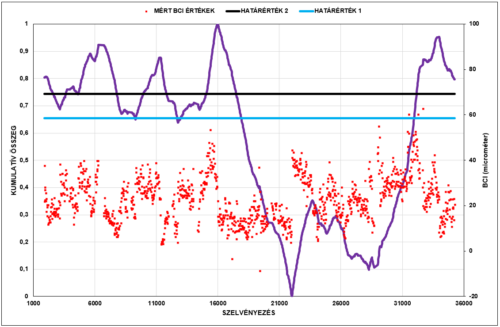
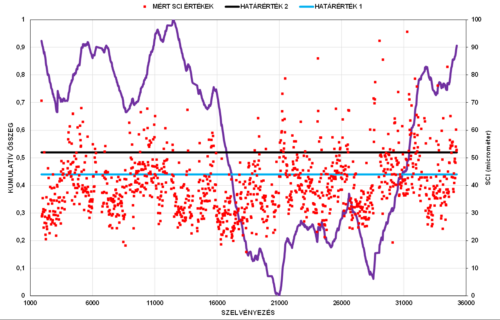
A forgalmi sávon a mért behajlásokból a két értéket a következő ábrákon vizsgálhatjuk.
A BCI értékek viszonya a határértékekhez – 33. ábra – és a homogenitása kielégítőnek látszik. Itt ne felejtsük el, hogy elméletileg egy idősor első tagját szemléljük.
Az SCI értékek esetében ugyanakkor a határértéken jelentős számban túllépő eseteket is találunk.
Ha a CBF érték „ugrálós” homogén szakaszaira emlékezünk, ez az SCI értékek hasonlóan nagy „változékonyságában” jelentkezik.
Nyilván lehet vitatni az értékek előírásában a mértéket, a tűréshatárokat, de a kép egy egyébként szerkezeti számként jó eredményeket mutató pályaszerkezetben meglévő potenciális hibákat mutatja.
 |
 |
Már csak ezért is érdemes volna a teljes szerkezetre, illetve annak fontos részeire vonatkozó minőségellenőrzésban a technológiának szerepet adni.
Az FWD technológiának az építéskivitelezés során minőségellenőrzési célú felhasználásáról a pályaszerkezeti rétegekről szóló írásban még visszatérünk.
Hivatkozások
[1]: e-UT 09.02.34 Dinamikus teherbírásmérés [KUAB]. Mérési eredmények feldolgozása
[2]: Hothan, J. & Schäfer, F. 2004. Analyse und Weiterentwicklung der Bewertung von Tragfähigkeitsmessungen. German. In: Straße und Autobahn 55.7. ISSN: 0039-2162, pp. 376- 382.
[3]: AASHTO Guide for Design of Pavement Structures 1993, Published by the American Association of State Highway and Transportation Officials, Washington DC
[4]: HUMU. 1971. Hajlékony útpályaszerkezetek méretezési utasítása. Techn. jel. 159215/1971. Budapest: Közlekedés- és Postaügyi Minisztérium, Közúti Főosztály, 31. old
[5]: https://map.mbfsz.gov.hu/
[6]: Szepesházi, R. és mtsai. 2003. Erősen térfogatváltozó talajokra épített Békés megyei utak geotechnikai vizsgálata, kézirat.
[7]: Pap, M., Mahler, A. & Tóth. Cs. 2017. Klimatikus viszonyok hatása a reziliens modulusra I.: Környezeti hatások és talajjellemzők meghatározása Útügyi Lapok 5. évfolyam 10. szám
[8]: Pap, M., Mahler, A. & Tóth, Cs. 2017. Klimatikus viszonyok hatása a reziliens modulusra II.: Reziliens modulus meghatározása Útügyi Lapok 5. évfolyam 10. szám
[9]: ÚT 2-1.202 [e-UT 06.03.13] Aszfaltburkolatú útpályaszerkezetek méretezése és megerősítése
[11]: Per. U. 1998. Modelling Flexible Pavement Response and Performance.
[12]: MSZ 2509/2 1989 CBR vizsgálat
[13]: Gary, W. Chai, Shanty Argadiba, G. Stephenson, I. Condric, E. Y. Oh, & Sittam P. Manoharan. 2013. Prediction of Subgrade CBR using FWD for Thin Bituminous Pavements, International journal of pavement research and technology, https://doi.org/10.6135/ijprt.org.tw/2013.6(4).280
[14]: Útgazdálkodási célú etalonszakasz-megfigyelés kiértékelése Kézirat Közlekedéstudományi Intézet Nonprofit Kft. Budapest – 2009. december
[15]: ÚT 2-2.121 [e-UT 09.02.33] Dinamikus behajlásmérés méretezéshez [KUAB]
[16]: Aitchison, G. D. & Richards, B. G. 1965. A broad scale study of moisture conditions in pavement subgrades throughout Australia – The selection of design values for soil suction equilibria and soil suction changes in pavement subgrades.” Moisture Equilibria and Moisture Changes in Soils beneath Covered Areas, A Symposium in Print, Australia Butterworths, 226-232
[17]: Y. Perera, C. Zapata. 2004. Long – Term Moisture Conditions under Highway Pavements Conference Paper in Geotechnikal Special Publication
[18]: A.A.A. Molenaar. 2007. Lecture Notes CT 4860, Structural Pavement Design, Design of Flexible Pavements, Delft
[19]: H. M. Park. 2001. Use of Falling Weight Deflectometer multi-load level data for pavement strength estimation North Carolina State University 2001
[20]: Boromisza, T., Gáspár, L. & Károly, R. 2008. Útpályaszerkezetek teherbírása, hazai és külföldi eredmények és problémák. Közúti és mélyépítési szemle 58. évfolyam 5-6. szám
[21]: Tóth, Cs. & Gáspár, L. 2018. A pályaszerkezet-teherbírást jellemző behajlás mérések feldolgozása során alkalmazott korrekciók megbízhatósága: Útügyi Lapok, 6. évfolyam, 11. szám
[22]: Abd El-Raof, Hossam S., Ragaa T. Abd El-Hakim, Sherif M. El-Badawy, & Hafez A. Afify. 2018. Structural Number Prediction for Flexible Pavements Using the Long Term Pavement Performance Data. International Journal of Pavement Engineering 21 (7): 841–55. https://doi.org/10.1080/10298436.2018.1511786
[23]: Emad Kassem Ahmed Muftah Abu Sufian Natalie Mikels, 2023. Simplified Analysis Methods of TSD and FWD Data for Effective Asphalt Pavement Preservation Program. Prepared for Idaho Transportation Department ITD Research Program, Contracting Services Highways Construction and Operations, University of Idaho.
[24]: A. C. Pronk. 1994. Equivalent Layer Theories. State of the arts report. DIENST WEG- EN WATERBOUWKUNDE [DWW] VAN DER BURGHWEG 1 DELFT, Netherlands 2628 CS.
[25]: Z. Soós & Cs. Tóth. 2016. Simple Overlay Design Method for Thick Asphalt Pavements Based on the Method of Equivalent Thicknesses Periodica Polytechnica Civil Engineering. https://doi.org/10.3311/PPci.9721
[26]: A.A.A Molenaar. 1983. Structural performance and design of flexible road constructions and asphalt concrete overlays. PHD dissertation University of Technology Delft
[27]: ÚT 2-1.202:2010, tervezet, „Aszfaltburkolatú útpályaszerkezetek megerősítésének méretezése” Elérhető online: http://www.mernökkapu.hu/fileok/2/
[28]: Primusz, P. & Tóth, Cs. 2023. Virtuális inerciapont módszeren alapuló útpályaszerkezet diagnosztikai eljárás elméleti alapjainak kidolgozása. Útügyi Lapok, 11. évfolyam, 18. szám. https://doi.org/10.36246/UL.2023.2.04
[29]: Noureldin, A. Samy. 1992 New Scenario for Backcakulation of Layer Moduli of Flexible Pavements, In Strength and Deformation Characteristics of Pavement Structures, 1384:23–28. Transportation Research Record. Transportation Research Board.
[30]: TLI Kft vezette munkabizottság. 2006. Nagy terhelésű utak pályaszerkezeteinek gazdaságos meghatározása, Kézirat.
Erre a szövegre így hivatkozhat:
Karoliny Márton: Pályaszerkezetek tulajdonságainak meghatározása FWD készülék segítségével. Második rész: Az elválaszthatatlan földmű és pályaszerkezet, DOI: 10.36246/UL.2024.2.03
