https://doi.org/10.36246/UL.2024.2.06
2024; 12. évfolyam, 20. szám
Pdf: Magyar német típus-pályaszerkezetek várható süllyedésének összehasonlítása
Bevezetés
Az útpályaszerkezetek méretezési alapelveit az [1] Útügyi Műszaki Előírás részletezi. E útügyi műszaki előírásban megadott, alapréteg-fajtánként és forgalmi terhelési osztályonként csoportosított típus-pályaszerkezeteknél a szükséges aszfaltréteg-összvastagságokat a többrétegű útpályaszerkezetek mechanikai modellje szerint, a hajlítási húzó és nyomó igénybevételeket figyelembe vevő fáradási kritériumok alapján méretezték. A tervezési élettartam végén hálós típusú fáradási repedések jelentkezhetnek. Az aszfaltburkolatok nyomvályúképződését a fáradási kritérium alapján való méretezés nem kezeli, ez ellen a várható forgalom nagyságának, igénybevételeknek és helyi klímának és a tervezési forgalomnak megfelelően megválasztott összetételű aszfalteveréket kell alkalmazni az ÚT 2-3.301 szerint. Ezek alapján megállapítható, hogy az e-UT06.03.13 azt feltételezi, hogy a nyomvályúképződés nem altalaj eredetű, ezt a megfelelő összetételű aszfaltkeverék megválasztásával kell megakadályozni.
Bizonyos műszaki előírások azt feltételezik, hogy ha a földmű tetején korlátozzuk a feszültséget [2]–[4] vagy az alakváltozást [5] akkor a földmű többlet alakváltozása az útpályaszerkezet élettartamának szempontjából várhatóan nem jelent kritikus igénybevételt. Mivel feszültségi- vagy alakváltozási kritériumban az alap- vagy javítóréteg nem játszik szerepet, ezért ezek a megközelítési módszerek azt feltételezik, hogy a nyomvályúképződés kizárólag altalaj eredetű.
Doktori disszertációjában Little helyszíni mérések alapján [6] megállapítja, hogy az állandó süllyedések nem csak altalaj eredetűek lehetnek, az aszfaltburkolat vastagságának függvényében a kötőanyag nélküli szemcsés alapréteg is jelentősen hozzájárulhat a süllyedésekhez. Helyszíni mérések alapján meghatározták [7], hogy a nyomvályú 68%-ban nem aszfalt eredetű. A szakirodalomban [8] alapján látható, hogy nincs általánosan elfogadott, széles körben elismert és dokumentált eljárás az útpálya alatti talajokban (alapréteg, javítóréteg és altalaj) fellépő süllyedések és így a nyomvályú mélységének meghatározására. Egyes módszerek [9] csak a szemcsés alapréteg deformációjára koncentrálnak, míg más esetben [10] az anyagállandók, ill. a paraméterek kalibrációja nincs dokumentálva, így eltérő peremfeltételek esetén nem tudjuk a modelleket használni. Kutatásukban [11] korszerű 3D végeselemes vizsgálatot végeztek a nyomvályú mélység meghatározására, ugyanakkor kizárólag az aszfaltra alkalmaztak a kúszást megengedő anyagmodellt, így az aszfalt alatti talajokban nem keletkezett utólagos tömörödés. Szintén korszerű végeselemes vizsgálatot végzett [12], [13] a talajokban kialakuló halmozódó maradó alakváltozásra. Az anyagállandókat ciklikus triaxiális vizsgálattal laboratóriumban határozták meg. Ugyanakkor mind két kutatásban a laboratóriumi vizsgálat csupán 1.000 ciklusig zajlott, amely számottevően kevesebb, mint az útpályaszerkezeteket érő tengelyterhelések száma.
A maradó alakváltozások vizsgálatakor olyan módszereket célszerű alkalmazni, amelyek képesek az ismétlődő forgalmi terhelésből minden talajréteg halmozódó maradó alakváltozását meghatározni, továbbá figyelembe vehetőek a különböző peremfeltételek. Az egyik legátfogóbb és legfejlettebb ilyen talajmodell a High-Cycle Accumulation (HCA) modell, melyet [14]-ben mutattak be és hitelességét számos laboratóriumi vizsgálattal akár 2 milliós ciklusszámig verifikálták [15]–[18]. Ezen okokból kutatásunkban a HCA modellt alkalmaztuk a nyomvályú mélységek meghatározására.
Kutatásunkban meghatároztuk egy-egy a német [19] és a magyar [1] útügyi műszaki előírások alapján méretezett típus pályaszerkezet talaj eredetű várható süllyedéseit. Választásunk két olyan típus-pályaszerkezetre esett, amelyek a tervezési forgalom szempontjából gyakorlatilag azonos igénybevételnek vannak kitéve. Kutatásunk másik részében a javító- és védőréteg vastagságával és anyagi minőségével foglalkoztunk. Mivel a hazai útépítési gyakorlatban a védőréteg vastagságok igen vékonynak tekinthetőek nemzetközi összehasonlításban, vizsgáltuk, hogy ezen rétegek vastagságának növelésével milyen mértékben tudjuk a várható nyomvályú mélységeket csökkenteni. A hazai útépítési gyakorlatban javító- és védőrétegnek gyakran kerül lekerekített szemcséjű folyami homokos kavics beépítésre a magasabb minőséget képviselő zúzottkő helyett. Bár a homokos kavics teherbírása rendszerint magasabb, mint a természetes altaljé, nedvességre és fagyra nem érzékeny, mégis kisebb a teherbírási, mint egy hasonló szemeloszlású zúzottkő. Tovább egyes tanulmányok szerint [20], [21] a lekerekített szemcsealak érzékenyebb az ismétlődő terhelésből kialakuló halmozódó maradó alakváltozásra, mint a tört szemcséjű zúzottkő. Kutatásunkban ennek a kérdéskörnek is utána jártunk.
Az alkalmazott számítási eljárás
A HCA modell
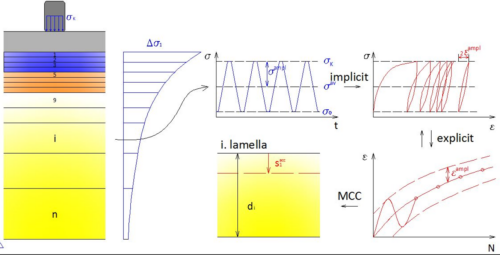
Nagy ismétlésszámú ciklikus terhelés esetén az alakváltozásokat direkt kiszámító implicit módszerek nem célravezetőek, mivel minden egyes terhelési ciklussal halmozzuk és továbbvisszük az anyagmodell és a számítási (integrálási) hibákat, emiatt legfeljebb N< 50 ciklus esetén használható megbízhatóan [22]. Emiatt az explicit megoldási módszerek kerülnek előtérbe, melyek empirikus alapon adják meg a ciklusszám – maradó alakváltozás \( (N-\varepsilon^{acc}) \) összefüggést. Az egyik legjobban dokumentált, számos laborvizsgálattal igazolt ilyen típusú anyagmodell az ismétlődő terhelésből származó maradó alakváltozások meghatározására a High-Cycle Accumulation (HCA) modell, melyet [14] publikáltak és Wichtman doktori disszertációjának [15] számos modellkísérletével verifikáltak. A modellt [20] habilitációja részletesen bemutatja, itt csak az érthetőség kedvéért a legfontosabb számítási lépcsőket ismertetjük.
A HCA-modell alapgondolata, hogy kombinálja az implicit, növekményen \( (\dot{\sigma}-\dot{\varepsilon}) \) alapuló fejlett anyagmodelleket és az explicit, ciklusszám – maradó alakváltozás modelljét \( (N-\varepsilon^{acc}) \). Első lépésben egy hagyományos fejlett anyagmodell segítségével meghatározzuk az állapotjellemzőket, mint a hézagtényező, az átlagos normálfeszültség, a feszültségállapot és a ciklikus alakváltozási amplitúdó \( (εampl) \). Ezek után az alakváltozási amplitúdó, mint bemenő adat segítségével meghatározzuk az explicit modellel a maradó alakváltozás növekményét (1). Drénezett esetben, amennyiben az átlagos feszültség nem változik, illetve, ha nem lép föl statikus értelemben vett képlékeny alakváltozás, a (1) egyenlet direkt a képlékeny alakváltozásnövekményt adja meg.
\[ {\dot{\varepsilon}}^{acc}=f_{ampl\ }{\dot{f}}_N\ f_e\ f_p\ f_Y\ f_\pi \]
A képlékeny alakváltozás növekményből a ΔN cikluscsomag hatására kialakuló maradó alakváltozást állandó \( ε^{ampl} \) mellett a (2) egyenlet adja. Mivel hosszú távon a talajszerkezetben és állapotjellemzőiben változások állnak be, ezért időnként az explicit számítást megszakítjuk és az úgynevezett kontroll ciklusokban megismételjük az implicit analízist, hogy \( ε^{ampl} \) aktuális értékével folytassunk további explicit számítást újabb ΔN cikluscsomagra.
\[ \Delta\varepsilon^{acc}={\dot{\varepsilon}}^{acc}\bullet\Delta N \]
A HCA modell a halmozódó alakváltozást mint vektormennyiséget adja meg, így az alakváltozás skalár nagyságán kívül szükségünk van még egy folyási törvényre, amely megadja az alakváltozás irányát (m), vagyis, hogy az alakváltozás milyen deviátoros εq és térfogatos εv részekből tevődik össze. Ezekből tudjuk majd származtatni a süllyedésszámításhoz szükséges függőleges alakváltozási komponenseket.
\[ \varepsilon^{acc} = \varepsilon^{acc}m \]
Saját kutatásunkban az altalajra a Modified Cam Clay (MCC) anyagmodell folyási törvényét alkalmaztuk [17] kutatási eredménye szerint. Zúzottkő alaprétegen végzett vizsgálatok [23] kimutatták, hogy a homoktól eltérően a tömörítés hatására az anyag anizotrop módon viselkedik, így nem érvényes a MCC folyási törvénye. A zúzottkő alapréteg és a javítóréteg esetén az ott bemutatott anizotrop folyási törvényt alkalmaztuk.
A halmozódó alakváltozásnövekmény vektor skalár részét leíró (1) egyenlet 5 empirikus tag fi szorzataként adódik. Az egyes fi tagok a főbb befolyásoló tényezőket írják le sorrendben a (rugalmas) alakváltozási amplitúdó \( f_{ampl} \), a ciklusok száma, ill. a talaj emlékezete \( {\dot{f}}_N \), a hézagtényező \( f_e \), az átlagos normálfeszültség \( f_p \) és a feszültségállapot \( f_Y \). A fent említett 5 fi függvényt a 7 darab \( C_i \) anyagállandóval írhatjuk le. Ezen felül szükségünk van még a folyási törvény és \( f_Y \) leírásához a kritikus súrlódási szögre \( \varphi_{cc} \), amely nem feltétlenük egyezik a monoton CU-triaxból számítható \( \varphi_c \) kritikus súrlódási szöggel. A ciklikus folyási törvény kritikus súrlódási szögének \( \varphi_{cc} \) meghatározására [17]-ban lévő ajánlásokat alkalmaztuk.
A HCA paramétereket a [16], [18] cikkekben bemutatott egyszerűsített kalibrálási eljárás szerint határoztuk meg, amely tiszta, szubgranuláris szemcséjű kvarc homok-kavics talajokra vonatkozik, továbbá a korrelációkra érvényesek az következő korlátok: 1,5 < CU < 8,0 illetve, 0,1 mm < d50 < 3,5 mm, Nmax = 2 106. A zúzottkő alapréteg és javítóréteg HCA paramétereit [23] szerint választottuk meg.
A lamellás számítási eljárás
Kutatásunkban a [24]–[26] modellek analógiáján egy egyszerűsített lamellás modell segítségével vizsgáltuk a pályaszerkezet süllyedéseit. A számítási modellt [27] részletezi, így itt csak a legfontosabb számítási lépéseket mutatjuk be. Az egyszerűsített számítási modell a konvencionális süllyedésszámításhoz használt lamellás módszerek analógiáján a talajt diszkretizálja, lamellákra bontja. Ezek után meghatározzuk a tengely- ill. kerékteherből származó feszültségeloszlást és megállapítjuk az egyes lamellákra jutó többlet függőleges feszültséget \( Δσ_{1,i} \), majd ebből az átlagos normálfeszültség, tömörség és alakváltozás függő nemlineáris merevség segítségével kiszámítjuk a lamellák középvonalában (a lamella felső és alsó paramétereinek átlagaként) az alakváltozásokat \( ε_i^{ampl} \). Ezt követően az \( ε_i^{ampl} \) mint bemenő paraméter segítségével meghatározzuk a halmozódó alakváltozásokat az egyes lamellákban \( ε_i^{acc} \), majd a lamellák vastagságával és ciklikus folyási törvény segítségével kiszámítjuk a süllyedéseket lamellánkként \( s_{1,i}^{acc}=m_1*\varepsilon_i^{acc}d_i \). A teljes süllyedés az egyes lamellák süllyedéseinek összegéből adódik \( Σs_{1,i}^{acc} \). A lamellás módszer számítási elvét az 1. ábra szemlélteti. Amint azt [27] bemutatja, a számítási módszer kellően pontos és megbízható eredményt szolgáltat mind a rugalmas alakváltozások, mind a maradó alakváltozásokra vonatkozóan. Az élettartam végén várható maradó süllyedésekben az altalaj és a terhelés osztály függvényében legfeljebb 2-7%-os különbséget mutattak ki az egyszerűsített módszer és a végeselemes számítási módszer között.
 |
Vizsgált pályaszerkezet és anyagmodellek
A vizsgált pályaszerkezet
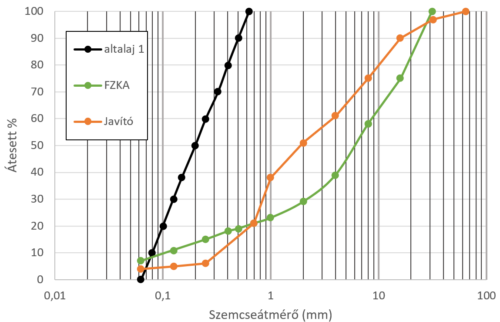
Kutatásunkban az 1. táblázatban látható a magyar e-UT06.03.13 „D” terhelési osztályának és a német RstO „III” terhelési osztályának előírt rétegrendje szerinti talaj eredetű, az ismétlődő egységtengely áthaladásából származó halmozódó maradó alakváltozását határoztuk meg. Az útszerkezetet 4 rétegű (homok altalaj, javítóréteg, FZKA és aszfaltburkolat) rendszerként modelleztük. A vizsgált altalaj egy szubgranuláris szemcséjű kvarc homoktalaj, melyek szemeloszlási diagrammja a 3.2 ábra látható. Vizsgálatainkban az altalajt Trρ=93%-os beépítési tömörségűnek feltételeztük. Az altalajra kerül a teherbírást biztosítandó 20 cm vastag teherbírásjavító réteg. A javítóréteg anyaga a [28] diplomamunkájában részletesen ismertetett 50-50%-os keverési arányú 0/11 tiszatarjáni kavicsos homok és 0/22 gyöngyössolymosi zúzottkő, szemeloszlási görbéje a 2 ábrán látható. A javítórétegre kerül az 1. táblázat szerinti vastagságú FZKA és aszfaltburkolat. A zúzottkő alapréteg HCA-paramétereire szakirodalmi adat csak a kolumbiai előírásoknak megfelelő zúzottkő alaprétegre érhető el, így ezt az anyagot választottuk vizsgálatainkban.
| Forgalmi tervezési osztály | |
| e-UT06.03.13 „D” osztály | RstO „III” osztály |
| Tervezési forgalom, TF, millió egységtengely | |
| 1-3 | 0,8-3 |
 |
 |
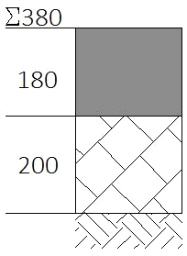
Az egyes műszaki előírások a teherbírási követelmények és az előírt rétegvastagságok tekintetében kis mértékben eltérnek egymástól. Az altalaj teherbírása pl. az osztrák, a német és a francia műszaki előírásban rendre \( E_{2min} \) = 35, 45 ill. 50 MPa, a zúzottkő tetején 120-150 MPa-os előírás érvényes. E tekintetben jelentős különbséget nem lehet felfedezni az e-UT06.03.13 és a nemzetközi műszaki előírások között. Amennyiben azonban az előírt rétegvastagságokat összehasonlítjuk a magyar műszaki előírással, látható, hogy a magyar utakra előírt vastagságok kisebbek. Különösen érvényes ez, ha a német [19] műszaki előírás nemzetközi viszonylatban is vastag pályaszerkezetével vetjük össze.
Mindkét vizsgált műszaki előírás a 10 tonnás egységtengely áthaladásokat veszi figyelembe a tervezési forgalom meghatározásakor, a „D” osztály esetén 1-3 millió áthaladást, míg a német „III” kategória esetén 0,8-3 millió áthaladást kell a pályaszerkezetnek az élettartam alatt elviselnie, így a terhelés részről nincsen eltérés. A földműtükrön a magyar esetben \( E_{2,m} \) > 40 MPa biztosítandó, míg a németeknél \( E_{2,min} \) > 45 MPa, ami szintén nem jelentős eltérést mutat. Amennyiben ez az érték az altalajon tartósan nem biztosítható, úgy javítóréteg beépítése szükséges. A lényeges különbség ez után látszik, hiszen a magyar műszaki előírás csupán 20 cm vastag FZKA alapréteget ír elő, míg a németeknél hasonló szemeloszlású anyag mellett legalább 53 cm vastag alaprétegre van szükség. További különbség, hogy a német előírás 4 cm-rel vastagabb aszfaltburkolatot ír elő a magyarral szemben, (18 cm vs. 22 cm). A pályaszerkezet így összességében a német esetben 37 cm-rel vastagabb azonos terhelési körülmények mellett.
A vastagabb rétegrend segít az abroncsból származó felszíni terhek jobb elosztásában. Ennek következményeként kisebb többlet függőleges feszültségek jutnak az egyes talajrétegekre, különösen a maradó alakváltozás szempontjából legérzékenyebb altalajra. Az eltérő rétegrendek következtében a kialakuló rugalmas alakváltozások a magyar esetben 60%-kal nagyobbak a zúzottkő tetején, és közel háromszoros mind a javítórétegben, mind az altalajon.
A vizsgált talajok és paramétereik
Az aszfaltburkolatot egyrétegű homogén anyagnak tekintettük, amelyet a terhelési osztálytól függő vastagságával, rugalmassági modulusával és Poisson tényezőjével jellemezhetünk. Az aszfalt merevségét az egyenértékű hőmérsékletnek megfelelően állandónak választottuk \( (E_a \) =4.000 MPa, \( υ_a \)=0,35 [29].
Az FZKA és javítóréteg Poisson tényezőjét szakirodalmi adatok [29] alapján vettük fel. Az altalaj esetén a Poisson tényező értéke sem az egyes lamellákban, sem a terheléskor nem állandó, értékét rugalmasságtani összefüggések és az anyag nyírási és összenyomódási modulusának ismeretében számíthatjuk.
A javítóréteg esetén feltételeztük, hogy azt Trρ=95%-os tömörségi fok mellett építik be. A javítóréteg sajátmodulusa a végeselemes visszaszámítás alapján [30] ca. 150 MPa, így a földmű tetején \( E_2,m \) ~ 60 MPa-os teherbírás várható. Az FZKA-nál Trρ=96%-os beépítési tömörségi fokot feltételeztünk. A FZKA sajátmodulusa végeselemes visszaszámítás alapján ca. 230 MPa [30], így az alapréteg tetején a várható teherbírás E2,b~ 120 MPa, amely megfelel a nemzetközi általános útépítési gyakorlatnak. A vizsgált talajok szemeloszlási diagramját a 2. ábrán az ehhez tartozó kezdeti főbb jellemzőket a 2. táblázat adja meg.
 |
| Talaj | d50
(mm) |
Cu
(-) |
emin
(-) |
emax
(-) |
ρdmax (g/cm3) | e0
(-) |
υ
(-) |
| altalaj 1 (L26) | 0,2 | 3,0 | 0,540 | 0,920 | 1,75 | 0,627 | 0,33-0,36 |
| javítóréteg | 2,0 | 11,9 | 0,364 | 0,513 | 2,06 | 0,340 | 0,40 |
| FZKA | 6,3 | 100,0 | 0,230 | 0,440 | 2,30 | 0,188 | 0,40 |
Az altalaj HCA-paramétereit a [16], [18]-ban ismertetett, a d50 és CU-tól függő összefüggések segítségével határoztuk meg. A zúzottkő esetén [23] vizsgálatai szolgáltatták az eredményeket. Az alkalmazott HCA paramétereket a 3. táblázat közli.
| Talaj | Campl | Ce | Cp | CY | CN1 | CN2 | CN3 | fcc |
| altalaj 1 (L26) | 1,70 | 0,513 | 0,47 | 2,26 | 5,49 10-3 | 1,30 10-2 | 2,38 10-5 | 32,76° |
| FZKA | 1,10 | 0,070 | -0,22 | 1,80 | 5,20 10-4 | 0,03 | 1,30 10-5 | 44° |
| Javítóréteg | 1,10 | 0,204 | -0,22 | 1,80 | 5,20 10-4 | 0,03 | 1,30 10-5 | 42° |
Alkalmazott anyagmodell az implicit számításnál
A HCA-modell érzékeny az \( ε^{ampl} \) bemenő adatra, ezért fontos, hogy ezt lehetőleg minél pontosabban, körültekintően számítsuk ki. Disszertációjában [26] megjegyzi, hogy alapvetően bármilyen anyagmodellel meghatározható az \( ε^{ampl} \) , törekedni kell azonban a (rugalmas) alakváltozások minél pontosabb leírására, ezért az alkalmazott anyagmodell vegye figyelembe a merevség tömörségtől, átlagos normálfeszültségtől és a kis alakváltozásoktól függő nemlinearitását.
Kutatásunkban az implicit számításoknál az altalajt nemlineárisan rugalmas, az átlagos normálfeszültség, a hézagtényező és a kis alakváltozásoktól függő merevséggel vettük figyelembe. Az altalaj maximális nyírómerevségét \( G_max \) és összenyomódási modulusát a [31], [32]-ban ismertetett a d50-től és CU-tól függő korrelációk segítségével határoztuk meg. A leromlási görbe a [33]-ban ismertetett, a CU-tól függő összefüggések segítségével állapítottuk meg. Mivel a merevség (G, E, M, υ) az átlagos normálfeszültségtől és az alakváltozástól is függ, ezért ezt minden lamellára, minden cikluscsomagban és minden egyes ciklus növekményi teherfelvitelekor meg kell határozni, hiszen folyamatosan változik. Ezen kívül minden egyes terhelési lépcső felvitelekor iterálással kell megállapítani a tényleges alakváltozás növekményt és az ehhez tartozó tényleges merevséget.
A hidraulikus kötőanyag nélküli szemcsés alaprétegek esetén a mérnöki gyakorlatban sokkal inkább a reziliens modulus MR használata terjedt el. A legegyszerűbb összefüggés MR meghatározására [34] egy nemlineárisan rugalmas anyagmodell:
\[ M_R=k_1\theta^{k_2} \]
A 4. táblázat a k1 és k2 tényezők tipikus tartományait mutatja be.
| Réteg | k1 (psi) | k1 (MPa) | k2 (-) |
| szemcsés alapréteg | 3000 – 8000 | 20,6 – 55,2 | 0,5 – 0,7 |
| szemcsés javítóréteg | 2500 – 7000 | 17,2 – 48,3 | 0,4 – 0,6 |
Az FZKA ill. javítóréteg esetén a merevséget a (4) képlet szerint számítjuk ki. Laborvizsgálatok híján a konkrét k-értéket mérnöki érzékkel a drénezettségi viszonyok és anyagjellemzők alapján kell meghatározni. A zúzottkő alaprétegnél a „k” paramétereket a 4. táblázatban megadott sávok átlagaként ( \(k1 \) =5.500 psi, \( k2 \) =0,6), míg a javítórétegnél kicsivel az átlag fölött (\( k_1 \) =5.000 psi, \( k_2 \) =0,55) vettük figyelembe. Utóbbi esetben a növelést az indokolja, hogy az alkalmazott anyag szemeloszlása és típusa (50%-os zúzottkő arány) mérnöki érzékkel inkább magasabb minőségűnek tekinthető, mint az átlagos javítóréteg anyaga.
Várható süllyedések számítási eredményeinek bemutatása
A számított süllyedés-ciklusszám görbéket a 3. ábra mutatja. Amint az a rétegvastagságok alapján is várható volt, a süllyedések jelentősen kisebbek a német előírások alapján épített utak esetén. Megállapítottuk, hogy a keréktengelyben számított süllyedések azonos tulajdonságú altalaj és azonos intenzitású és ismétlésszámú forgalmi terhelésből a magyar e-UT06.03.13 „D” forgalmi terhelési osztályának előírt rétegrendjével 1,96-szor nagyobbak, mint a német RStO „III” kategóriájának rétegrendje. A vastagabb rétegrend segít a forgalmi terhelésből származó feszültségek kedvezőbb elosztásában, így a halmozódó alakváltozásra különösen érzékeny altalajban számottevően kisebb reziliens alakváltozások alakulnak ki. Mivel a megfigyelések alapján a reziliens ciklikus alakváltozás arányos a kialakuló képlékeny halmozódó alakváltozással, így a képlékeny alakváltozások is számottevően kisebbek lesznek. Várható továbbá, hogy a vastagabb zúzottkő alapréteg és leginkább a vastagabb aszfaltburkolat következtében a süllyedéskülönbségek és így a nyomvályú mélysége nem csak abszolút értelemben, hanem arányában is kisebb lesz, hiszen a vastagabb burkolati rétegek jobban szétosztják a feszültségeket, így a kerék nyomvonalán kívül eső részekre relatív nagyobb feszültség jut, így a süllyedéskülönbségek, valamint a pályaszerkezeti süllyedéskülönbségek mérséklődnek.
Fontos megállapítás továbbá, hogy sok anyagmodellel ellentétben saját vizsgálataink szerint a maradó alakváltozások az élettartam alatt folyamatosan halmozódnak és nem csengenek le teljesen, bár a halmozódás intenzitása egyre kisebb. A magyar rétegrend esetén a pályaszerkezet élettartamának végére közel 23 mm süllyedés alakul ki a zúzottkő tetején, amely már közlekedésbiztonsági kérdéseket is felvet. A német előírások vastagabb rétegrendje következtében azonos terhelés esetén is csupán 12 mm-re adódott a keréktengelyben számolt süllyedés a zúzottkő tetején.
A számított süllyedések elméleti értékek, amelyek valóságban való megjelenését számos tényező befolyásolja, tompítja. A maradó alakváltozások mértéke nagyban függ az áthaladó teher nagyságától, amit részben kompenzál az egységtengelyre való átszámítás, de a valódi forgalom és annak összetétele sok esetben nem ismert. Szintén a számított maximális süllyedés és a süllyedéskülönbségek kialakulását csökkenti a gépjárművek forgalmi sávokban való eltérő nyomvonalon haladása. Az aszfalt különböző hőmérséklet mellett eltérő merevséggel rendelkezik, ami miatt eltérő feszültségeket ad át az altalajra. A számítások során alkalmazott referencia hőmérséklet a nyári és az őszi/tavaszi időszak közötti feszültséget eredményez, így az év háromnegyed részében kisebb feszültségek, azaz kisebb alakváltozások is fognak bekövetkezni [36]. A létrejövő halmozódó alakváltozások megjelenését ezért nem egy markáns nyomvályúként célszerű elképzelni, hanem az a süllyedési horpa és előbb említett hatások miatt a számítottnál kisebb süllyedéskülönbségekként jelennek majd meg a burkolat tetején. Az is elképzelhető, hogy ezek a süllyedéskülönbségek repedésekké fajulnak, így azok helyett repedések jelennek meg a burkolat tetején.
 |
Javítóréteg anyaga és minősége
Az eredmények alapján a süllyedések döntő hányada az altalajban, annak is leginkább a felső zónájában alakul ki. Megvizsgáltuk, hogy az altalaj legfelső zónájának javítórétegre való talajcseréjével, hogy csökkenthetők a süllyedések. A vizsgálatban az „E” terhelési osztályra és a „talaj 1” altalajra kiszámítottuk a várható süllyedéseket úgy, hogy a javítóréteg vastagságát 0,2-0,4-0,6-0,8-1,05 m között változtattuk. A javítóréteg legfelső 20 cm-e mindig, mint töltés értendő, az ennél nagyobb vastagság pedig mint talajcsere. A számított süllyedés-N görbéket a 4. ábra mutatja. Az ábra alapján megállapítottuk, hogy a javítóréteg vastagságának növelésével hatékonyan tudjuk csökkenteni a maradó süllyedéseket, a 85 cm többlet javítóréteggel a végső süllyedéseket közel a felére (55%-ra) tudjuk csökkenteni, de már 40 cm többlet javítóréteg is elegendő a süllyedések 30%-os redukálásához.
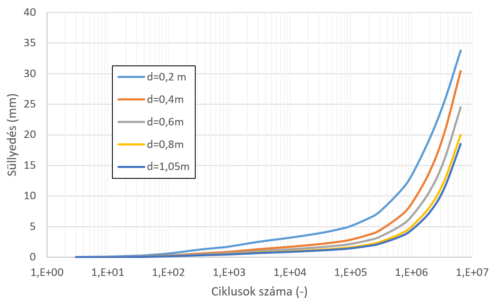 |
A 4. ábra alapján látható továbbá, hogy a d=0,8 m és a d=1,05 m-es görbék szinte egybeesnek, csupán a terhelés utolsó szakaszában válnak kis mértékben szét. Ez azt jelenti, hogy a javítóréteg vastagságának növelésével egy határ süllyedéshez tartunk, és a javítóréteg vastagságának további növelése már nem hatékony. E hatást szemlélteti az 5. ábra, amely kiválasztott ismétlésszámok esetére mutatja be a számított süllyedéseket a javítóréteg vastagságának függvényében. Az 5. ábrán látható, hogy az élettartam végén számított süllyedéseket a javítóréteg vastagságának növelésével kezdetben közel azonos hatékonysággal tudjuk csökkenteni, hiszen a számított függvény meredeksége kezdetben közel azonos, majd d=0,8 m után a görbe ellaposodik. Gazdaságossági megfontolások alapján megállapítható, hogy a süllyedések hatékony csökkentéséhez célszerű d=0,8 m-t választani, amely az FZKA d=0,2 m-es vastagságával együtt egy 1,0 m vastag durvaszemcsés szerkezeti réteget jelent az aszfaltréteg alatt.
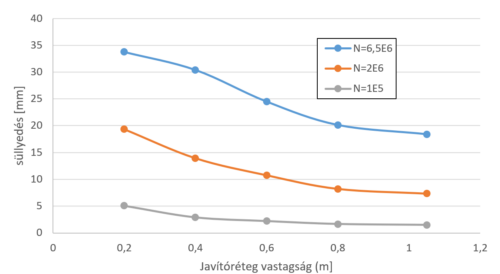 |
A 6. ábra az egyes rétegekben számított süllyedések százalékos arányát szemlélteti a teljes süllyedéshez képest. Ezek alapján megállapítottuk, hogy az altalaj süllyedésekhez való hozzájárulási aránya továbbra is mértékadó, a d=0,2 m-nél számított ca. 94%-ról a javítóréteg növelésével d=1,05m-nél kb. 75%-ig csökkenthető. Ennek oka, hogy az „E” terhelési osztályban a mélyebb talajrétegekben is számottevő süllyedések alakulnak ki, amelyek többszörösen felülmúlják a javítóréteg süllyedéseit.
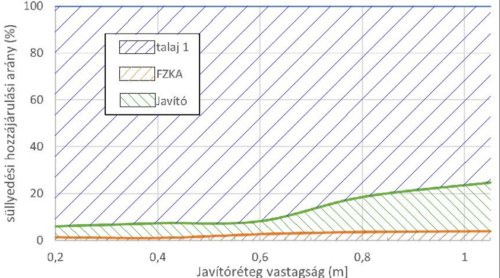 |
Az útépítési gyakorlatban a javítóréteget bizonyos esetekben nem zúzottkőből, hanem szokványos folyami homokos kavicsból építik. A HCA-paraméterek azonban erősen függenek a szemcsék alaki tulajdonságaitól [20], [21], és az egyes paraméterek döntően eltérnek annak függvényében, hogy törtszemcsés vagy természetesen lekopott, szubgranuláris anyagról van e szó. Ennek érdekében paramétervizsgálatot végeztünk a zúzottkő anyagára vonatkozón, és kiszámítottuk a különböző ágyazati vastagságok mellett a süllyedéseket törtszemcsés, természetes szubgranuláris szemcséjű és ezek 50%-50%-os keverési arányú anyagokra. A természetes szubgranuláris szemeloszlású anyag HCA-paramétereit a [16], [18] által közölt korrelációk és a talaj szemeloszlási paraméterei (CU és d50) alapján határoztuk meg. A Ce paramétert változatlannak feltételeztük, mivel ez a lehető legtömörebb állapotot leíró hézagtényezőt jelöli. Fontos megjegyezni, hogy a Wichtmann-féle egyszerűsített paramétermeghatározás csak CU £ 8 esetére lett kalibrálva, és mivel a javítóréteg CU=11,9-es egyenlőtlenségi mutatója ezen kívül esik, ezért a kapott eredményeket csak fokozott óvatossággal lehet értelmezni. Az 50%-50%-os keverési arányú anyag HCA-paramétereit a törtszemcsés és lekerekített szemcséjű anyag átlagaként számítottuk. Az alkalmazott HCA-paramétereket az 5. táblázat közli. Ezen kívül feltételeztük, hogy a pillanatnyi viselkedést, merevségi tulajdonságokat és így az alakváltozási amplitúdót a javítóréteg anyaga nem befolyásolja. Ez csak közelítésként fogadható el, hiszen a gyakorlatból ismert tény, hogy a zúzottkőből készült ágyazatok teherbírása 15-40%-kal nagyobb, mint az azonos vastagságú homokos kavics ágyazat [35].
| Talaj | Campl | Ce | Cp | CY | CN1 | CN2 | CN3 | fcc |
| tört anyag | 1,10 | 0,204 | -0,22 | 1,80 | 5,20 10-4 | 0,03 | 1,30 10-5 | 42° |
| lekerekített anyag | 1,70 | 0,204 | 0,21 | 2,98 | 1,32 10-2 | 1,01 10-2 | 3,53 10-5 | 42° |
| 50%-50% kevert anyag | 1,40 | 0,204 | 0,00 | 2,39 | 6,48 10-3 | 2,00 10-2 | 2,41 10-5 | 42° |
A fent bemutatott anyagokra számított süllyedéseket a javítóréteg vastagságának függvényében a 7. ábra szemlélteti. A lekerekített és kevert szemcséjű anyag süllyedéseit is hatékonyan tudjuk csökkenteni a javítóréteg vastagságának növelésével, a lefutás azonos a zúzott anyagra tett megállapításokkal, a d=0,8 m fölötti vastagság növelés már nem tekinthető gazdaságosnak. Az eredmények alapján megállapítottuk, hogy a javítóréteg anyaga döntő jelentőségű, a törtszemcsés és lekerekített szemcséjű anyagok süllyedése között kétszeres a különbség, de a kevert anyag is 60%-kal nagyobb süllyedéseket szenved, mint tisztán törtszemcséjű. Érdemes megfigyelni, hogy a lekerekített anyagú javítóréteg még d=1,05 m esetén is nagyobb süllyedéseket szenved, mint a d=0,2 m vastag törtszemcséjű javítóréteg. Bár az eredményeket a fent részletezett okokból kisebb fenntartással kell kezelni, egyértelműen látszik, hogy a szemcsealak, amelyet a gyakorlatban oly sokszor figyelmen kívül hagynak és kizárólag a szemeloszlási görbére koncentrálnak kritikus jelentőséggel bír. Ennek megfelelően megállapítottuk, hogy süllyedések és nyomvályú mélységének hatékony csökkentéséhez a jó minőségű, tört anyagú zúzottkőből készült ágyazat elengedhetetlen.
 |
Összefoglaló
A hajlékony pályaszerkezetek méretezése leggyakrabban az útügyi műszaki előírások szerinti típus pályaszerkezetek segítségével történik, ugyanakkor az analitikus módszerek is egyre nagyobb teret nyertek az utóbbi időben, melyek segítségével gazdaságosabb pályaszerkezet érhető el. A méretezési eljárások ugyanakkor leginkább az aszfalt fáradási kritériumait vizsgálják, a nyomvályú mélységének meghatározása a nemzetközi gyakorlatban is háttérbe szorul. A legtöbb nemzeti műszaki előírás megelégszik azzal, hogy ha a kivitelezéskor betartják az előírt minőségi és építési követelményeket, illetve, ha a földmű tetején bizonyos feszültségi vagy alakváltozási korlátokat betartunk, akkor a földmű függőleges összenyomódása az útpályaszerkezet élettartamának szempontjából várhatóan nem jelent kritikus igénybevételt. Az évtizedes geotechnikai megfigyelések szerint ugyanakkor, ha a talajokat hosszan tartó ismétlődő terhelés éri, akkor még megfelelő betömörítés és alacsony terhelési intenzitás mellett is kialakulnak halmozódó maradó alakváltozások. Ezekből a relatív alacsony intenzitású tengelyterhekből a gyakran milliós, tízmilliós áthaladás következtében az évtizedes használat alatt mégis jelentős maradó alakváltozások alakulnak ki az aszfalt alatti talajokban.
Kutatásunkban összehasonlítottuk a magyar e-UT06.03.13 Útügyi Műszaki Előírás szerinti típus pályaszerkezetek teherbírás követelményeit a nemzetközi empirikus alapokon nyugvó méretezési eljárásokkal. Összehasonlítottuk a magyar e-UT06.03.13 „D” forgalmi terhelési osztály rétegrendjét az azonos forgalmi terhelésű német RstO „III” kategóriájú rétegrendjével és megállapítottuk, hogy a német előírás sokkal szigorúbb mind a zúzottkő alaprétegre, mind az aszfalt vastagságára vonatkozóan. Számításaink szerint a keréktengelyben számított süllyedések azonos tulajdonságú altalaj és azonos intenzitású, 2 millió ismétlésszámú forgalmi terhelésből a magyar e-UT06.03.13 „D” forgalmi terhelési osztályának előírt rétegrendjével 1,96-szor nagyobbak, mint a német RStO „III” kategóriájának rétegrendje által számított süllyedések.
A javító- és védőréteg vastagságára vonatkozó vizsgálatainkkal kimutattuk, hogy a várható süllyedések hatékonyan csökkenthetőek a javítóréteg vastagságának növelésével. Gazdaságossági szempontból a d=0,8 m-es javítóréteg vastagság fölött már nem érhető el érdemi redukció a süllyedésekben. A javítóréteg anyagára és a szemcsealak minőségére vonatkozó számításainkkal megállapítottuk, hogy a süllyedéseket a javítóréteg anyaga döntően befolyásolja és a törtszemcsés és lekerekített szemcséjű anyag süllyedése között közel kétszeres a különbség. Az eredmények tükrében célszerű a süllyedések és nyomvályú mélységének hatékony csökkentéséhez nem csak a javítóréteg vastagsága, de a jó minőségű, tört anyagú zúzottkőből készült ágyazat is elengedhetetlen.
Megállapítható továbbá, hogy a német előírások védőréteg vastagságára, különös tekintettel a tört szemcsék alkalmazására megfelelőnek tűnik. Számításainkkal továbbá összhangban van és nagyon jó új gyakorlatnak tűnik a hazai autópálya és gyorsforgalmi utakra vonatkozó 1 m vastag védőréteg, mivel így a teherbírási geotechnikai kockázatok minimálisra csökkenthetők. A tanulmányaink alapján célszerű lenne pontosítani a hazai UME előírásokat a védőréteg vastagságra vonatkozóan.
Hivatkozások
[1]: e-UT06.03.13, Aszfaltburkolatú útpályaszerkezetek méretezése és megerősítése e-UT06.03.13 (ÚT 2-1.202), Útügyi Műszaki Előírás. Magyar Útügyi Társaság, 2017.
[2]: W. D. Powell, J. F. Potter, H. C. Mayhew, and M. E. Nunn, 1984. THE STRUCTURAL DESIGN OF BITUMINOUS ROADS, TRRL Lab. Rep., no. 1115, Art. no. LR 1132 Monograph, Accessed: Jul. 05, 2022. [Online]. Available: https://trid.trb.org/view/211702
[3]: RDO -Asphalt 09, Richtlinien für die rechnerische Dimensionierung des Oberbaus von Verkehrsflächen mit Asphaltdeckschicht. 2009.
[4]: Shell, SHELL SPDM-PC User manual. Shell pavement design method for use in a personal computer, Version 1994, Release 2.0. 1994.
[5]: Austroads, Guide to Pavement Technology Part 2: Pavement Structural Design. 2019.
[6]: P. H. Little, 1993. The Design of Unsurfaced Roads Using Geosynthetics, Ph.D. dissertation, Nottingham, 1993.
[7]: J. Morris, 1973. The prediction of permanent deformation in asphalt concrete pavements, USA Transp. Group, 1973.
[8]: A. K. Singh & J. P. Sahoo, 2021. Rutting prediction models for flexible pavement structures: A review of historical and recent developments, J. Traffic Transp. Eng. Engl. Ed., vol. 8, no. 3, pp. 315–338, https://doi.org/10.1016/j.jtte.2021.04.003
[9]: S. Werkmeister, 2003. Permanent Deformation Behaviour of Unbound Granular Materials in Pavement Constructions, Ph.D. értekezés, TU Dresden, Drezda.
[10]: J. Uzan, 2004. Permanent Deformation in Flexible Pavements,” J. Transp. Eng., vol. 130, no. 1, pp. 6–13, https://doi.org/10.1061/(ASCE)0733-947X(2004)130:1(6)
[11]: G. Leonardi & F. Suraci, 2022. A 3D-FE Model for the Rutting Prediction in Geogrid Reinforced Flexible Pavements, Sustainability, vol. 14, no. 6, p. 3695, https://doi.org/10.3390/su14063695
[12]: H. Qi et al. 2022. Study on Deformation Characteristics of Low-Highway Subgrade under Traffic Load, Appl. Sci., vol. 12, no. 7, p. 3406, https://doi.org/10.3390/app12073406
[13]: P. Zhou et al. 2022. Study on Deformation Characteristics of Extended Highway in Operation Period,” Adv. Civ. Eng., vol. 2022, pp. 1–13, https://doi.org/10.1155/2022/5496999
[14]: A. Niemunis, T. Wichtmann, & Th. Triantafyllidis, 2005. A high-cycle accumulation model for sand, Comput. Geotech., vol. 32, no. 4, pp. 245–263, https://doi.org/10.1016/j.compgeo.2005.03.002
[15]: T. Wichtmann, 2005. Explicit Accumulation Model for Non-cohesive Soils under Cyclic Loading. in Schriftenreihe des Institutes für Bodenmechanik der Ruhr-Universität Bochum, no. 38. Bochum.
[16]: T. Wichtmann, A. Niemunis, & T. Triantafyllidis, 2015. Improved simplified calibration procedure for a high-cycle accumulation model, Soil Dyn. Earthq. Eng., vol. 70, pp. 118–132, https://doi.org/10.1016/j.soildyn.2014.12.011
[17]: T. Wichtmann, A. Niemunis, & T. Triantafyllidis, 2014. Flow rule in a high-cycle accumulation model backed by cyclic test data of 22 sands, Acta Geotech., vol. 9, no. 4, pp. 695–709, https://doi.org/10.1007/s11440-014-0302-7
[18]: T. Wichtmann & T. Triantafyllidis, 2015. Inspection of a high-cycle accumulation model for large numbers of cycles (N=2 million), Soil Dyn. Earthq. Eng., vol. 75, pp. 199–210, https://doi.org/10.1016/j.soildyn.2015.04.008
[19]: RStO, “Richtlinie für die Standardisierung des Oberbaues von Verkehrsflächen.” Forschungsgesellschaft für Straßen- und Verkehrswesen, 2001.
[20]: T. Wichtmann, 2016. Soil behaviour under cyclic loading – experimental observations, constitutive description and applications, habilitáció.
[21]: T. Wichtmann, Th. Triantafyllidis, & L. Späth, 2019. On the influence of grain shape on the cumulative deformations in sand under drained high-cyclic loading, Soils Found., vol. 59, no. 1, pp. 208–227, https://doi.org/10.1016/j.sandf.2018.11.001
[22]: A. Niemunis, 2003. Extended hypoplastic models for soils, habilitáció, INSTITUTES FÜR GRUNDBAU UND BODENMECHANIK DER RUHR-UNIVERSITÄT BOCHUM, Bochum. Accessed: May 09, 2022. [Online]. Available: http://www.deutsche-digitale-bibliothek.de/item/7BOJPX4FLIFBAV7JBDELM6EVGSSB5GEY
[23]: T. Wichtmann, H. Rondón, A. Niemunis, T. Triantafyllidis, & A. Lizcano, 2010. Prediction of Permanent Deformations in Pavements Using a High-Cycle Accumulation Model, J. Geotech. Geoenvironmental Eng., vol. 136, https://doi.org/10.1061/(ASCE)GT.1943-5606.0000275
[24]: A. Häcker, 2013. Erweiterung eines Lamellenmodells für zyklisch belastete Flachgründungen, diplomamunka, Karlsruher Institute für Technologie, Institute für Bodenmechanik und Felsmechanik, Karlsruhe.
[25]: T. Wöhrle, 2012. Überprüfung und Entwicklung einfaher Ingenieurmodelle für Offshore-Windenerigealagen auf Bass eines Akkumulationsmodells, diplomamunka, Karlsruher Institute für Technologie, Institute für Bodenmechanik und Felsmechanik, Karlsruhe.
[26]: H. Zachert, 2015. Zur Gebrauchstauglichkeit von Gründungen für Offshore-Windenergieanlagen. in Veröffentlichungen des Institutes für Bodenmechanik und Felsmechanik am Karlsruher Institut für Technologie (KIT), no. 180. Karlsruhe: Karlsruher Institut für Technologie (KIT).
[27]: M. J. Vamos & J. Szendefy, 2023. Calculation Method for Traffic Load-Induced Permanent Deformation in Soils under Flexible Pavements, Geotechnics, vol. 3, no. 3, pp. 955–974, https://doi.org/10.3390/geotechnics3030051
[28]: A. Káli, 2020. Ipari padlók ágyazatként és útépítési védőrétegként használt durvaszemcsés talaj sajátmodulusának numerikus modellezése, B.Sc. diplomamunka, BME, Budapest.
[29]: Útügyi Lapok, “Kutatási jelentés: Tervezési útmutató: Aszfaltburkolatú útpályaszerkezetek méretezésének alternatív módszere,” 2016.
[30]: M. J. Vámos & J. Szendefy, 2023. Overconsolidated Stress and Strain Condition of Pavement Layers as a Result of Preloading during Construction Period. Polytech. Civ. Eng., https://doi.org/10.3311/PPci.22258
[31]: T. Wichtmann & T. Triantafyllidis, 2010. On the influence of the grain size distribution curve on P-wave velocity, constrained elastic modulus Mmax and Poisson’s ratio of quartz sands,” Soil Dyn. Earthq. Eng., vol. 30, no. 8, pp. 757–766, https://doi.org/10.1016/j.soildyn.2010.03.006
[32]: T. Wichtmann & T. Triantafyllidis, 2009. Influence of the Grain-Size Distribution Curve of Quartz Sand on the Small Strain Shear Modulus Gmax, J. Geotech. Geoenvironmental Eng. ASCE, vol. 135, no. 10, pp. 1404–1418.
[33]: T. Wichtmann & T. Triantafyllidis, 2013. Effect of Uniformity Coefficient on G/Gmax and Damping Ratio of Uniform to Well-Graded Quartz Sands, J. Geotech. Geoenvironmental Eng., vol. 139, no. 1, pp. 59–72, https://doi.org/10.1061/(ASCE)GT.1943-5606.0000735
[34]: AASHTO, AASHTO Guide for Design of Pavement Structures. American Association of State Highway and Transportation Officials, 1993.
[35]: J. Szendefy, 2019. Földművek teherbírásának meghatározási lehetőségei és teherbírásjavító módszerek ismertetése, presented at the MAÚT 25 éves, Budapest.
[36]: M. J. Vámos & J. Szendefy, 2023. Tempeature Effects on Traffic Load-Induced Accumulating Strains in Flexible Pavement Structures, Int. Journal of Pavement Research and Technology https://doi.org/10.1007/s42947-024-00466-4
Erre a szövegre így hivatkozhat:
Vámos Máté János, Szendefy János: Magyar német típus-pályaszerkezetek várható süllyedésének összehasonlítása, 2024, DOI: 10.36246/UL.2024.2.06
