https://doi.org/10.36246/UL.2022.1.03
2022; 10. évfolyam, 16. szám
Bevezetés
Hagyományosan a talajnedvesség-meghatározási módszerek a gyakorlatban időigényesek és roncsolással járnak. Még manapság is hiányosság tapasztalható a kis, (<0,01 m2) valamint a nagy léptékű (>100m2) mérések közötti, tehát közepes léptékű (0,01-100 m2) sekély felszín alatti talajtulajdonságok feltárásárának lehetőségei terén [1]. Itt fontos tisztázni a talajnedvesség-tartalom fogalmát.
A talajnedvesség-tartalom, mint több tudományterület kulcsparamétere (angolban: SWC = soil water content) konkrétan a térfogati talajvíztartalomra utal, ami a víztérfogatának, a teljes talajtérfogathoz viszonyított arányát jelenti egy egységre vonatkoztatva [1], [2], [3].
A tajnedvességtartalom meghatározására szolgáló technikák közül kiemelendők a geofizikai eljárások, amelyek minimálisan vagy teljesen roncsolásmentesek, és hatalmas területi lefedettséget képesek megvalósítani a talaj tulajdonságainak meghatározásához. Nagy vonalakban két fő kategória különböztethető meg, nevezetesen a talaj elektromos vezetőképességét [4], [5] mérők, valamint azok a módszerek, melyek során az elektromágneses hullámoknak a talajba történő kibocsájtása, majd detektálása történik. Ilyen, az utóbbi kategóriába sorolható altípus a földradar vagy talajradar (angolban: GPR = ground penetrating radar).
A GPR rendszerek előnye, hogy a hagyományos módszerekkel (pl. termogravimetrikus eljárás, időtartománybeli reflexiómérés) szemben az úthálózatok állapota rövidebb idő alatt felmérhető, és roncsolásmentes eszközként lehetővé teszi a pályaszerkezetek állapotának, a földmű minőségének, ill. nedvesség okozta pályaszerkezeti károknak a kiértékelését, így az eljárás előnyös a burkolaton megfigyelhető úthibák megelőzésében. Mindez elősegíti a döntéstámogatást és a fenntartási munkák hatékonyabb kezelését.
Lényeges az alsóbbrendű mezőgazdasági utak, valamint az agro-erdészeti rendszereket kiszolgáló utak, illetve az erdők feltáróhálózata esetén a környezeti jellemzőinek alaposabb vizsgálata, mivel az időjárásnak való kitettség a vékonyabb pályaszerkezet miatt ezeknél az úthálózatoknál erőteljesebben érezteti hatását
Jelen cikk célja áttekintést adni a GPR alapú talajnedvesség-tartalom meghatározásának lehetőségeiről földművek esetében és részletesen bemutatni a szakirodalmat.
Alapelvek és GPR konfigurációk a talajnedvesség-tartalom mérések esetén
A földradar, terepi gyakorlatban nagy hatékonysággal alkalmazható eszköz, mivel nagyobb talajtérfogat mérésére alkalmazható (cm3-m3), amely előnyőssé teszi a Bevezetésben már említett szabványos pontmérési technikákkal szemben (pl.: TDR (time-domain reflectometry) és a kapacitás szonda) [6], [7], [8], [9], [10], [11]. A GPR emellett olyan roncsolásmentes geofizikai eljárás, amely nagy felbontási lehetőséget, jelentős behatolási mélységet biztosít a közepes léptékű talajnedvesség méréseknél [2], valamint jobb időhatékonyággal alkalmazható más roncsolással járó és roncsolásmentes eljárásokkal összehasonlítva [1].
A vizsgálandó közegben lévő anyagok tulajdonságainak észlelésére a GPR nagyfrekvenciás elektromágneses (EM) hullámokat használ (általában 10 és 1200 MHz közötti középfrekvenciákon) [12]. A GPR adó egysége általában EM hullámimpulzusokat továbbít a vizsgálandó közegbe, és a vevő egysége a visszavert jeleket fogadja az idő függvényében. Ezt a kialakítást bisztatikusnak nevezik [13].
A GPR két kulcsparamétere annak felbontása, és behatolási mélysége. A felbontást a GPR által kibocsájtott impulzus időtartama határozza meg, amit pedig a GPR rendszer frekvenciájának sávszélessége. A GPR felbontása, a központi frekvenciájával párhuzamosan növekszik [14]. A feltárható mélység a vizsgálandó talaj elektromos konduktivitásától, valamint a GPR központi frekvenciájától függ. Alacsony vezetőképességű közeg (pl. száraz homok, kavics) esetén az alacsony frekvenciás (50 vagy 100 MHz antennájú) GPR rendszerek néhány 10 méteres, míg a magas frekvenciás típusok (450 vagy 900 MHz) pár méteres behatolási mélységet képesek elérni. Kőzetlisztes homok és agyag esetén a behatolási mélység jelentősen csökken. A GPR tehát kifejezetten érzékeny a talajtextúrára, valamint az elektromos vezetőképességre, ezáltal a sikeres alkalmazhatóságának területe redukálódik [13].
Az EM-hullámterjedés miatt a visszavert jelek hasznos információkat tartalmaznak a vizsgált közegről a dielektromos állandó változás, és ehhez kapcsolódóan a kétirányú futási idő (two-way travel time), amplitúdó, hullámforma és fázis tekintetében. A talajközeg esetén a visszavert jelek tulajdonságait főként a talaj dielektromos állandó értéke befolyásolja, amely pedig erősen talajnedvesség függő.
A dielektromos állandó egy „valós” és egy képzetes részből tevődik össze, amelyet komplex dielektromos állandónak nevezünk.
\[ ε^{*}= ε_{r}-jε^{”} \]
ahol
\( ε^{”} \): a dielektromos állandó ’képzetes’ része, amely az energiaeloszláshoz kapcsolódik.
A GPR mérések esetén a sávszélesség értéke alapvetően 10 MHz és 1 GHz közé esik, amely tartományban értéke tipikusan kicsi \( ε_{r} \)-hez képest, így a vizsgált közeg dielektromos állandója a következőképpen határozható meg:
\[ ε_{r}= \frac{ε}{ε_{0}} \]
ahol
\( ε_{r} \): egy anyag dielektromos állandója
\( ε_{0} \): vákuum dielektromos állandója
A dielektromos állandó valós része ( \( ε_{r} \) ) egy anyag elektromos térerősség-tárolási kapacitását adja meg a vákuumhoz viszonyítva.
A dielektromos állandó értékében nagy különbségek vannak, így a cseppfolyós halmazállapotú víz értéke 78-88 között változik a hőmérséklet függvényében (az édesvíz pl. ~80), az egyéb talaj alkotó, mint a levegő értéke ~1, vagy szilárd fázisok, kb. 3-10 közöttiek [13], [3], [15]. A három talajalkotó fázis közti jelentős dielektromos állandóban való különbség elsősorban a vízmolekulák magas polarizálhatóságának köszönhető [1].
Ez, a talajban levő dielektromos állandóban való jelentős értékkülönbség a fő oka a GPR-ek talajnedvesség-tartalom mérőeszközeként való használatának [2].
Az 1. táblázat áttekintést ad a különböző anyagok dielektromos állandóiról.
| Anyag | Dielektromos állandó |
| Levegő | 1 |
| Desztillált víz | 80 |
| Édesvíz | 81 |
| Durva törmelék, feltöltés | 6-12 |
| Beton | 7 |
| Aszfalt | 3-4 |
| Pályaszerkezet | 8 |
| Homok földmű | 4-6 |
| Kavics földmű | 4-7 |
| Bitumennel stabilizált alapréteg | 6-7 |
| Cementstabilizált réteg | 8-10 |
| Nedves talaj | 30 |
| Fagyott talaj | 6 |
| Száraz, homokos talaj | 3 |
| Nedves, homokos talaj | 19-25 |
| Száraz, iszapos talaj | 2,5 |
| Nedves, iszapos talaj | 19 |
| Száraz, agyagos talaj | 2 |
| Nedves, agyagos talaj | 15-25 |
| Agyag | 5-40 |
| Kőzetliszt | 10 |
| Köves talaj | 7 |
Tekintettel arra, hogy a GPR-ek által kibocsájtott hullámok minden irányba terjednek, ezért egy anomália (pl. vízzel töltött csővezeték a talajban) esetén az arról visszaverődő hullámok előbb érik el a vevőegységet, minthogy a GPR közvetlenül fölötte legyen. A radarképen ezen visszavert hullámok hiperbolaként jelennek meg, mert a példában közvetlenül az említett anomália felett végzett mérés során visszaverődő hullám esetén a legrövidebb az út (idő), és ehhez képest minden más hullám által megtett út hosszabb. A hiperbola domborúságát a talajban levő átlagos hullámsebesség határozza meg (vagyis azt határozza meg, mennyivel hosszabb idő szükséges a hullámoknak az extra távolság megtételéhez [13].
GPR antenna rendszerek és mérés technikák
A gyakorlatban jelenleg 3 talajnedvesség-mérésre alkalmazható GPR antenna rendszert alkalmaznak: földkapcsolt (ground-coupled), levegőkapcsolt (air-coupled) és a fúrólyuk típus (borehole GPR) [2].
A földkapcsolt GPR esetén (ahol a talajjal az antenna teljes kontaktban van, ezáltal nagy behatolási mélységet eredményezve) 3 méréstechnika típust különböztethetünk meg:
- Rögzített távolság (Fix-offset (FO)): rögzített antenna-távolságot tart fenn az adó és a vevőegység között, amelyeket egyszerre mozgat a mérési vonalon.
- Szélesszögű visszaverődés és refrakció (wide-angle reflection and refraction (WARR)): egységközönként növeli a távolságot az adó és a vevő között, de az adót rögzített pozícióba tartva.
- Közös-középpont (CMP): egységközönként növeli az adó, és a vevő közötti távolságot (mindkettőt mozgatva), de egy közös középpontot fenntartva.
A WARR és CMP módszereket közös néven „multi-offset” (MO) módszernek (többszörös távolság módszer) nevezik [9].
Ellentétben a talajkapcsolt GPR-rel, a levegőkapcsolt GPR esetén az adatgyűjtés egy meghatározott felszín feletti magasságra beállított antenna segítségével történik [2].
 |
Fúrólyuk GPR: két fúrólyuk között kivitelezett mérés, vagy a felszínről a fúrólyukba [19].
A fúrólyuk GPR-ok esetén a következő három mérési technika (1b. ábra) terjedt el: zéró távolság profil (zero-offset profile (ZOP)), több távolságot alkalmazó profil (multi-offset profile (MOP)) és vertikális radarprofil (vertical radar profile VRP).
- ZOP: a mérés során, a felszín alatti szelvényadatok gyűjtéséhez az adó és a vevő egységet külön-külön fúrásban egyidejűleg mozgatják azonos mélységen egységes lépésközzel [2].
- A MOP módszer esetén a vevő egység mozgatása történik a fúrólyukban, miközben az adót a másik fúrólyuk bizonyos mélységében rögzítik egy részmérésben. Majd a következő részmérésben egységnyi lépésközzel haladva az adót is mozgatják, így az egy következő fixpontba kerül [2].
- A VRP méréshez csak egy furat szükséges és fúrólyukba ereszkedő vevőről történik az adatgyűjtés, míg az adó egység a talajfelszínen rögzített [1].
A ZOP és MOP méréseket „fúrások közötti” (interhole) vagy keresztfúrásos (cross-borehole) módszereknek is nevezik, mert az adatgyűjtés két fúrólyuk között történik [2].
A módszerek felosztásának további lehetősége aszerint történik, hogy a talajnedvesség-tartalom meghatározására egy antennatávolságból történik (egytávolságos módszer (single-offset method) (FO és ZOP módszerek)), vagy több mérésből, különböző antennatávolságokkal (Több távolság alapú módszerek (multi-offset method) (CMP és WARR módszerek)) [1]. Mindkét esetben a mérés mélységét ismernünk kell.
GPR alapú talajnedvesség-mérés módszerek
Számos, a nedvességérzékelést célzó GPR-alapú módszert fejlesztettek ki különböző alkalmazási területekre [20], [21] és anyagokra, mint például betonszerkezetekre [22], természetes talajokra [23], [24], valamint hengerelt aszfaltkeverékekre [25].
Az elmúlt évtizedekben a földradar (GPR) egy elterjedt mérőeszköze volt a telítetlen zónák hidrológiájának és a vízerőforrások vizsgálatának [1]. A számos felhasználási terület közül kiemelendő a talajnedvesség-tartalom mérés [6], [13], [26].
A GPR-alapú SWC mérési módszerek területén Xinbo és mtsai 2019 [2] rendszerbe foglaltan mutatják be a közelmúltban elért kutatási eredményeket a visszavert hullám (reflected wave), a talajhullám (ground wave), a felszíni visszaverődés (ground wave), a fúrólyuk GPR (borehole GPR), teljes hullámforma inverzió (full waveform inversion), átlagos burkológörbe amplitúdó (average envelope amplitude) és frekvencia eltolás (frequency shift) módszerek esetén. Xinbo és mtsai 2019 [2] ezen módszereket a vonatkozó alapelvek, előnyök, korlátok és alkalmazási lehetőségek tekintetében részletezik.
Módszerek osztályozása
A GPR alapú talajnedvesség-mérési módszerek végén felsoroltakat a 2. táblázat rendszerezi.
| Módszer osztályozása | Méréstechnika | Radar rendszer konfiguráció | Alkalmazott jeltulajdonság | SWC becslés referencia mélység tartománya | Referencia antenna frekvenciák | |
| Dielektromos állandón alapuló módszerek | Talajhullám módszer | CMP, WARR;
FO, MO kombináció |
Talajkapcsolt GPR | Idő | ≤30 cm | – 225/450/900
225/450 1500 200 (MO) – 225; 450; 450/900; 100/450 (FO)
|
| Visszavert hullám módszer | MO;
FO |
Talajkapcsolt GPR | Idő | A visszaverő-dő felület mélysége | 450; 400/200; 400; 250; 450; 900; 225/450/900; 225/450/900/1200; 1000; 100; 250; 200/400 | |
| Fúrólyuk GPR módszer | VPR;
ZOP; MOP |
Fúrólyuk GPR | Idő | Az adó és a vevő közötti maximális távolság, fúrólyuk mélység | 100;250;100; 200 (VPR; ZOP)
100;200 (MOP) |
|
| Felszínivisszaverődés módszer | Levegőkap-csolt GPR | Amplitúdó | ≤2 cm | 500; 1000 | ||
| Teljes hullámforma inverzió | –
WARR, CMO; MOP, VPR |
SFWC föld feletti monosztatikus GPR;
Földkapcsolt GPR; Fúrólyuk GPR |
A rögzített jel minden tulajdonsága | ~2 cm (SFWC)
– – |
1000-2000 (SFWC)
– 70/200; 100 – 100/150; 160; 250; 200; 250; 200 |
|
| Átlagos burkológörbe amplitúdón alapuló módszer | FO | Talajkapcsolt GPR | Amplitúdó és hullámforma | ≤30 cm (a a talajban levő radarjel hullámhosszával azonos nagyságrend) | 250; 250/500; 250; 1000; 200 | |
| Frekvencia tartomány analízis | Frekvencia eltolás módszer | FO | Talajkapcsolt GPR | Energia és fázis stb. | 10 cm | 600 |
A felvázolt 7 módszer közül egyedül a frekvencia eltolás módszer esetén, a GPR adatokból direkt módon a frekvenciából történik adatkinyerés.
Az összes többi eljárás (lásd 2. táblázat) a dielektromos állandón alapuló módszerek közé sorolható, mert ezek a talaj dielektromos állandóját igyekeznek első körben meghatározni, majd abból helyszíni kalibrációval, vagy empirikus összefüggés segítségével a talajnedvességre következtetni úgynevezett petrofizikai (kőzetfizikai) összefüggés segítségével. A petrofizikai összefüggéseknek 3 csoportja ismeretes:
- Empirikus összefüggések, pl.: [27], [28], [29], [30], [31], [32]
- Térfogati keverés formulák, pl.: [33], [34], [35], [36], [37].
- Effektív közeg megközelítések, pl.: [38], [39], [40], [41], [42], [43], [44], [45], [46], [47].
Kőzetfizikai összefüggések
Empirikus összefüggések
A terepi és laboratóriumi méréseken alapuló, empirikusan levezetett összefüggések kevésbé összetettek, mint a fizikai modellek, ezért könnyebben alkalmazhatók számos talajszerkezetre és víztartalom-feltételre, mivel a talaj szerkezeti tulajdonságairól (pl. térfogatsűrűség, porozitás, pórusszerkezet stb.) csak korlátozott információt igényelnek [3].
Az empirikus típus legelterjedtebb példája a Topp egyenlet [27], [48], [49], [3].
\[ θ_{soil}=-5,3*10^{-2}+2,92*10^{-2}ε_{r}-5,5*10^{-4}ε^{2}_{r}+4,3*10^{-6}ε^{3}_{r} \]
ahol: \( θ_{soil} \) térfogati talajnedvesség
Gerhards és mtsai. 2008 [11] arra a következtetésre jutottak, hogy ez az összefüggés megfelelően alkalmazható a levegőszárazságtól, a víztelítettségig terjedő nedvességviszonyok között, 0,013 m3 m-3 előrejelzési hibával.
A Topp egyenlet tehát empirikus módon lett a különböző fizikai talajféleségekre (különböző textúrával rendelkező ásványi talajokra) meghatározva. Pontossága Jacobsen és Schjønning 1994 [50] validációja alapján: 0,022 m3 m-3
A Topp egyenlet elsősorban homokos talajok esetén alkalmazható [27] [51].
Nadler és mtsai 1991 [28] a különböző víztartalmú rétegek egymásra helyezésének (pl. száraz a nedvesen, nedves a szárazon) hatásait vizsgálta iszapos vályogban TDR szondák segítségével. Az eredményeik a következő empirikus összefüggésre vezettek:
\[ θ=-7,25*10^{-2}+3,67*10^{-2}ε_{r}-12,3*10^{-4}ε^{2}_{r}+15*10^{-6}ε^{-3}_{r} \]
Nadler és mtsai 1991 [28] eredményeinek fő következtetése, hogy módszerükkel pontos víztartalom meghatározás végezhető TDR szondatípustól és talajrétegzettségtől függetlenül, kivéve, ha nagyon száraz talaj kerül nagyon nedves fölé [3].
Curtis 2001 [32] a dielektromos tulajdonságait mérte számos száraz térfogatsűrűséggel rendelkező talajminta esetén, 100 MHz-es frekvencián működő koaxiális átviteli-reflexiós berendezéssel, és a következő harmadrendű polinomot javasolták:
\[ θ=-2,86+2,435ε_{r}-3,421*10^{-2}ε^{2}_{r}+2,37*10^{-4}ε^{-3}_{r} \]
Curtis 2001 [32] rámutatott, hogy a talaj víztartalmának mérési pontossága a jel frekvenciájától függ, és a térfogati víztartalmat 10%-kal alulbecsüli az általuk javasolt egyenlet (5) a nagyfrekvenciás (pl. 500–1000 MHz) méréseknél, amennyiben a dielektromos állandó értéke is nagy egyúttal (pl. \( ε_{r} \) ≥ 30).
Más kutatók a talaj szerkezetének, sűrűségének és szervesanyag-tartalmának hatásait igyekeztek közvetlenül beépíteni a dielektromos állandó mérésébe az empirikus összefüggések kialakítása során. Erre jó példa a [30] által kifejlesztett szabványos harmadrendű polinom.
\[ θ=-7,01*10^{-2}+3,47*10^{-2}ε_{r}-11,6*10^{-4}ε^{2}_{r}+18*10^{-6}ε^{-3}_{r} \]
Az összefüggést használva, a TDR mérések alapján talajmintákból 0,012 m3 m−3 előrejelzési hibával számolhatunk. [30] egy továbbfejlesztett harmadrendű polinomot javasolt, amely magában foglalja a száraz térfogatsűrűség (g∙cm-3), az agyagtartalom (% w/w) és a szerves anyag (OM, % w/w) hatását:
\[ θ=-3,41*10^{-2}+3,45*10^{-2}ε_{r}-11,4*10^{-4}ε^{2}_{r}+17,1*10^{-6}ε^{-3}_{r}-3,70*10^{-2}ρ_{b}+7,36*10^{-4}(agyag)+47,7*10^{-4}(OM) \]
A Jacobsen és Schjønning 1993 [30] által fejlesztett összefüggéseket a durvaszemcséstől egészen a homokos agyag és vályog talajtextúrákig tesztelték. A száraz térfogatsűrűség, agyagtartalom és a szerves anyagtartalom hatásának figyelembevétele a becslési hibát 0,0097 m3 m-3-ra csökkentette.
Térfogati keverés formulák
A talajnedvesség-tartalom és a dielektromos állandó közötti kimondottan elméleti alapú megközelítések, minden talajösszetevőnek a térfogati frakcióit és a dielektromos állandóját veszik alapul a kapcsolat felállítására. Ilyen típusú modell CRIM (Complex Refractive Index Model) modell, amelyben a talaj-levegő-víz rendszer dielektromos állandója [33], [43], [44], [35], [36], [37], [52] a következő képlettel fejezhető ki:
\[ ε_{b} = [θε^{α}_{w}+(1-n)ε^{α}_{s}+(n-θ)ε^{α}_{a}]^{\frac{1}{α}} \]
ahol n: talaj porozitás (m3 m-3), \( ε_{w} \) , \( ε_{s} \) , \( ε_{a} \) : víz, talaj részecskék és a levegő dielektromos állandója, α: az elektromos mező orientációját meghatározó faktorszám, amely a vizsgálandó közeg geometriáját figyelembe veszi.
α értékei a következők lehetnek: α = 1, ha az elektromos mező párhuzamos a talajrétegekkel. α = -1, amennyiben az elektromos mező merőleges a talajrétegekre, és α = 0,5, ha izotropikus a közeg. Ezen utóbbi azt jelenti, hogy a fáziskeverékeken keresztülhatoló hullám futási ideje egyenlő a fázisalkotókon áthaladó hullámok térfogatsúlyozottan figyelembe vett futási idejének összegével [1].
(8) egyenlet átrendezésével a talajnedvesség-tartalom kifejezhető a következő szerint:
\[ θ = \frac{ε^{α}_{b}-(1-n)ε^{α}_{s}}{ε^{α}_{w}-ε^{α}_{a}-ε^{α}_{a}} \]
\( ε_{a} \) = 1, és α = 0,5, akkor az egyenlet a következő szerint redukálódik.
\[ θ = \frac{1}{\sqrt{ε_{w}}-1}\sqrt{ε_{b}}-\frac{(1-n)\sqrt{ε_{s}}-n}{\sqrt{ε_{w}}-1} \]
A (10) egyenlet fizikai értelmezése egy szimpla talajnedvesség-dielektromos állandó összefüggés révén [53] szerint:
\[ θ = a\sqrt{ε_{b}}-b \]
ahol a, b: kalibrációs paraméterek.
Dobson és mtsai 1985 és Roth és mtsai 1992 [35], [29], valamint Patriarca és mtsai 2014 [54] kutatásaik a térfogati keverés módszerekre megállapították, hogy agyagos talajban nedves kondíciók esetén megbízhatatlanok lehetnek tekintettel az agyag duzzadóképességére. Ez konkrétan az elektromos tulajdonságok alulbecsléséhez vezet a modell esetén.
Jacobsen és Schjønning 1994 [50] ásványi talajokon végzett független validációs kutatása alapján a (11) összefüggés pontossága: 0,0188 m3 m-3.
Effektív közeg megközelítések
Ezen módszerek figyelembe veszik egy kompozit anyag minden komponensének texturális és szerkezeti hozzájárulását ezen kompozit anyag dielektromos állandójához. Az effektív közegmegközelítés módszerek mikroléptékű geometriai modelleken alapulnak, amelyek a heterogén rendszerre vonatkozó texturális és szerkezeti információkat használnak fel a dielektromos tulajdonságok meghatározására. Az ilyen módszereken alapuló kutatások rámutattak, hogy egy közeg dielektromos tulajdonságainak a porozitás és a víztartalom függvényében való modellezésével nem érhető el megfelelő pontosság a nedvességbecslésben [3]. Az irodalomban található különféle effektív közegközelítés módszerek közül az [55] által javasolt EMA megközelítés egy hozzávetőleges víztartalom-permittivitás összefüggést ad, amelyet az effektív közegközelítés alkalmazásával kapunk véletlenszerű fáziskeverékben. Ez utóbbi modellezése a Multi-Indicator modellen keresztül történik változó sugarú gömbelemekkel. A számítás menetét a következő egyenletet adja:
\[ θ = \frac{(ε_{w}+2ε_{r})[(ε_{a}+2ε_{r})(ε_{r}-ε_{s})+3ε_{r}ϕ(ε_{s}-ε_{a})]}{2ε_{r}(2ε_{r}+ε_{s})(ε_{w}-ε_{a})} \]
ahol ϕ : talaj porozitás,\( ε_{a} \) , \( ε_{w} \) , \( ε_{s} \) : az anyagtérfogat dielektromos állandója, : levegő, vízkomponens, és talajmátrix dielektromos állandó értéke.
A frakciók relatív térfogata: \( n_{s}=1-ϕ \) (szilárd térfogat frakció), \( n_{w}=0 \) (térfogati víztartalom), \( n_{a}=ϕ-θ \) (levegőtérfogat frakció). A levegő és a víz dielektromos állandó értékei fixáltak, és amennyiben az összes porozitás adott, a (12) egyenlet már csak a szilárd fázis dielektromos állandójának függvénye.
Visszavert hullám módszer
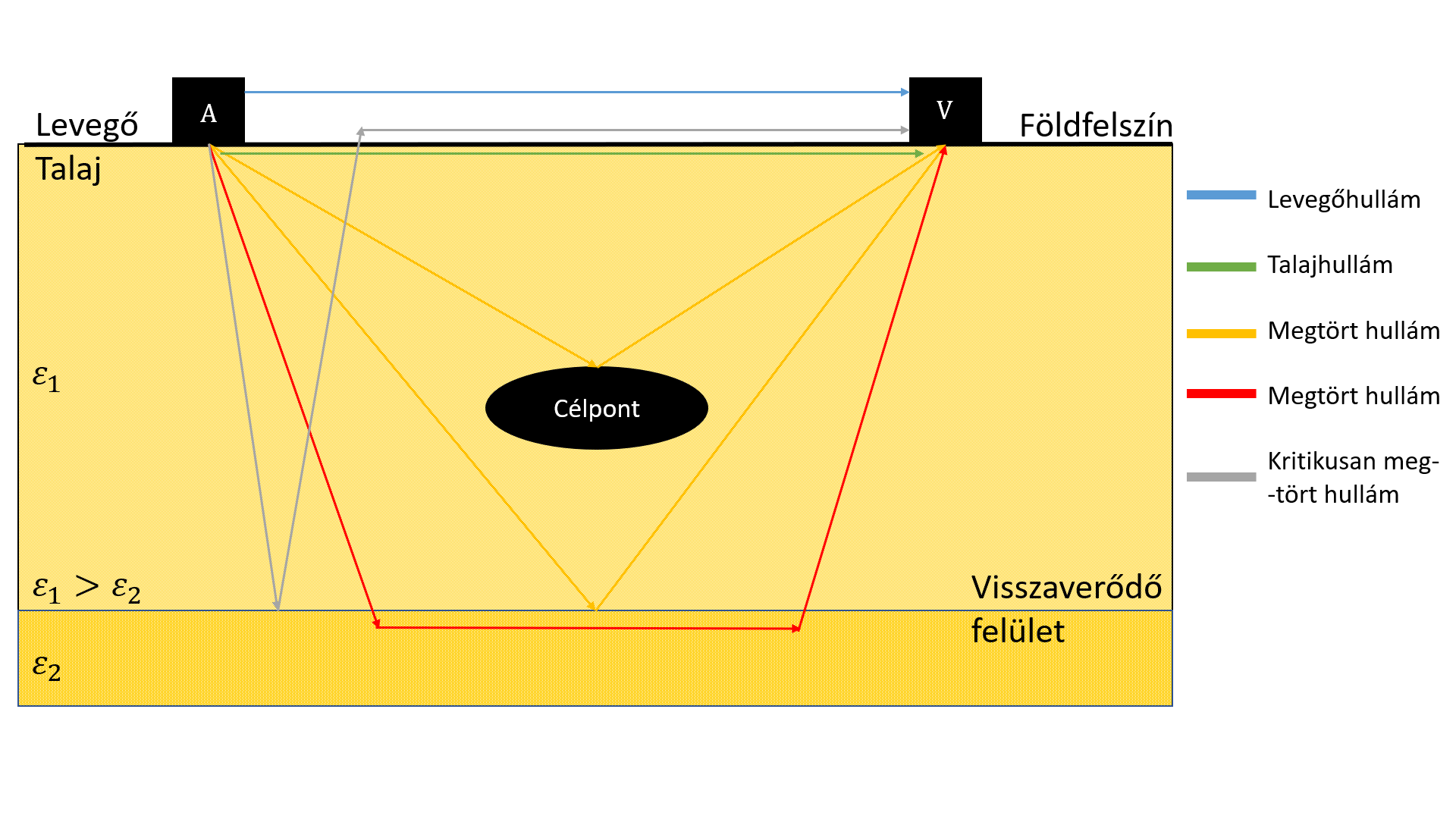
A visszavert hullám módszer esetén, a visszavert hullámadatok rögzítésére elsősorban földkapcsolt GPR-t alkalmaznak. A 2. ábrán vázolt módon, a GPR által kibocsájtott EM hullámok, miután visszaverődésen, átvitelen és hullámtörésen mentek keresztül a levegőben és két talajrétegen, akkor különböző módokon érik el a vevőt, így azok levegő, talaj, visszavert és megtört hullámként funkcionálnak. [13] szerint a visszavert hullámsebesség a talaj elektromos értelemben vett áteresztőképességétől (dielektromos állandójától) függ, amennyiben nemmágneses, alacsony vezetőképességű talajról beszélünk:
\[ v_{soil}=\frac{c}{\sqrt{ε_{soil}}} \]
ahol \( v_{soil} \): a visszavert hullám talajban való átlagos terjedési sebessége, \( ε_{soil} \): talaj dielektromos állandója, c: elektromágneses hullám vákuumban való terjedési sebessége 2·108 ms-1
Megjegyezzük, hogy a képlet speciális eset, amennyiben tehát ott a relatív mágneses permeabilitás = 1.
A módszer során a visszaverő felület (talajnedvesség) mélységét ismerni kell, melyet a GPR mérésén túl külön kell kivitelezni [56], [57]. Ismert mélység esetén tehát a vevőegységbe érkező hullámok idejéből (amely tehát ez esetben a talajnedvességről verődik vissza) könnyedén kiszámítható a vadózus zóna átlagos talajnedvesség-tartalma a következő összefüggés segítségével:
\[ v_{soil}=\frac{2d}{t_{rw}} \]
ahol: \( t_{rw} \) a visszavert hullám kétirányú futásideje, d: talajvízszint mélység [13]
Amikor az antennatávolság jelentős, akkor a (14) egyenlet a következőképpen módosul egytávolságos módszerek esetén [1]:
\[ v_{soil} = \frac{2\sqrt{d^{2}+(0,5a)^{2}}}{t_{rw}} \]
ahol a: antennatávolság [13]
A talajnedvesség tehát (14) és (15) egyenlet segítségével határozható meg, ha meghatározása a GPR jel felhasználásával történt. Az így kiszámított SWC a talajfelszín és a visszaverő felület közti talajnedvességet reprezentálja (tehát annak a talajszelvénynek, amin átmegy a hullám).
A módszer fő lépései:
- Visszaverődés adatok gyűjtése GPR segítségével
- Az átlagos terjedési sebesség meghatározása a visszaverő felület felett.
- Az átlagos terjedési sebesség konvertálása a talaj dielektromos állandójává, majd az SWC meghatározása.
 |
Miután visszaverő felület kiválasztásra került, az átlagos terjedési sebesség meghatározása pl. FO (fixed offset) segítségével történhet. Konkrét menete, hogy a visszaverő felület mélységet elosztják a visszaverődő hullám egyutas futási idejével (one-way travel time) [7], [50], [58], [8] majd az adatokat, a radarképen megjelenő visszaverődési hiperbolákhoz illesztik [13].
A fenti módszer mellett, az MO méréstechnika alkalmazásával az átlagos terjedési sebességet, a normál futási sebesség elemzése (normal move-out velocity analysis) révén is kiszámíthatjuk, de az intervallumsebesség-profilok is meghatározhatók Dix-egyenlettel [59], [3].
\[ v_{int,n}=\sqrt{\frac{t_{rw,n}v^{2}_{soil,n}-t_{rw,n-1}v^{2}_{soil,n-1}}{t_{rw,n}-t_{rw,n-1}}} \]
ahol \( v_{soil,n} \) átlagos terjedési sebesség a felszíntől a legalsó rétegig (n), \( v_{soil, n-1} \), átlagos terjedési sebesség a felszíntől az alsó rétegig (n-1), \( t_{rw} \) kétutas futási idő (n) réteg aljáig, \( t_{rw-1} \) kétutas futási idő (n-1) réteg aljáig, n =1 a talaj felső rétege.
A két mérési eljárás (FO és MO) tekintetében az FO (fixed offset) mérés előnye az egyszerű kivitelezhetőség és a kényelmes adatfeldolgozás, és így alkalmas a nagy területen, és helyben (in situ) történő SWC feltérképezésre [8]. Az FO mérés alkalmazása azonban előre ismert mélységű visszaverő felületet követel. Az MO-méréssel részletes SWC feltárás kivitelezhető a vertikális talajprofilban, és lehetővé teszi a talajfelszín és a visszaverő felület közötti átlagos terjedési sebesség mérését, még akkor is, ha a vizsgálandó (visszaverő) felület mélysége ismeretlen. Az adatgyűjtési folyamat hátránya viszont az FO-hoz képest annak jelentős időigénye.
Összefoglalva, a visszavert hullám módszerrel egyszerűen, viszonylag nagy talajmélységben lehetséges az SWC feltérképezése. A módszer nagy hátránya, hogy a számított SWC-k eloszlása a visszaverő felület helyzetétől függ. Így egy adott talajréteg talajnedvesség-tartalma nem határozható meg direkt módon.
Talajhullám módszer
A talajhullám módszer és az előzőekben bemutatott visszaverthullám-módszerek alapja hasonló. Mindkét eljárás talajkapcsolt GPR-t használ az adatgyűjtéshez (2. ábra).
A talajhullám módszer azonban korlátozott mélységű felszínközeli talajon képes áthaladni a visszaverthullám-módszerhez képest (2. ábra), ezáltal az SWC becslést csak korlátozott mélységben teszi lehetővé. [7] kutatásai alapján a talaj felső 20 centiméterében tárható fel a talajnedvesség-tartalom, függően a felszíni körülményektől és műszer beállításoktól. A behatolási mélység (h) azonban nem szigorúan meghatározott, három különböző képlettel számítható [60], [56], [61].
\[ h=0,5*\frac{c}{f*ε^{\frac{1}{2}}_{soil}} \]
\[ h=0,5 * \sqrt{c*\frac{s}{f*ε^{0,5}_{soil}}} \]
\[ h=0,145 * \sqrt{\frac{c}{f*ε^{0,5}_{soil}}} \]
ahol f: GPR középfrekvencia, s: antenna távolság
[62] kutatásai alapján a talajhullám módszerrel csupán 20 cm-es mélységben volt mérhető az SWC (450, 900 MHz középfrekvenciák mellett).
A talajhullám-módszer esetén FO és MO méréstechnika egyaránt alkalmazható a talajhullám terjedési sebességének meghatározásra, amit később dielektromos állandóvá konvertálnak, majd az SWC-t határozzák meg.
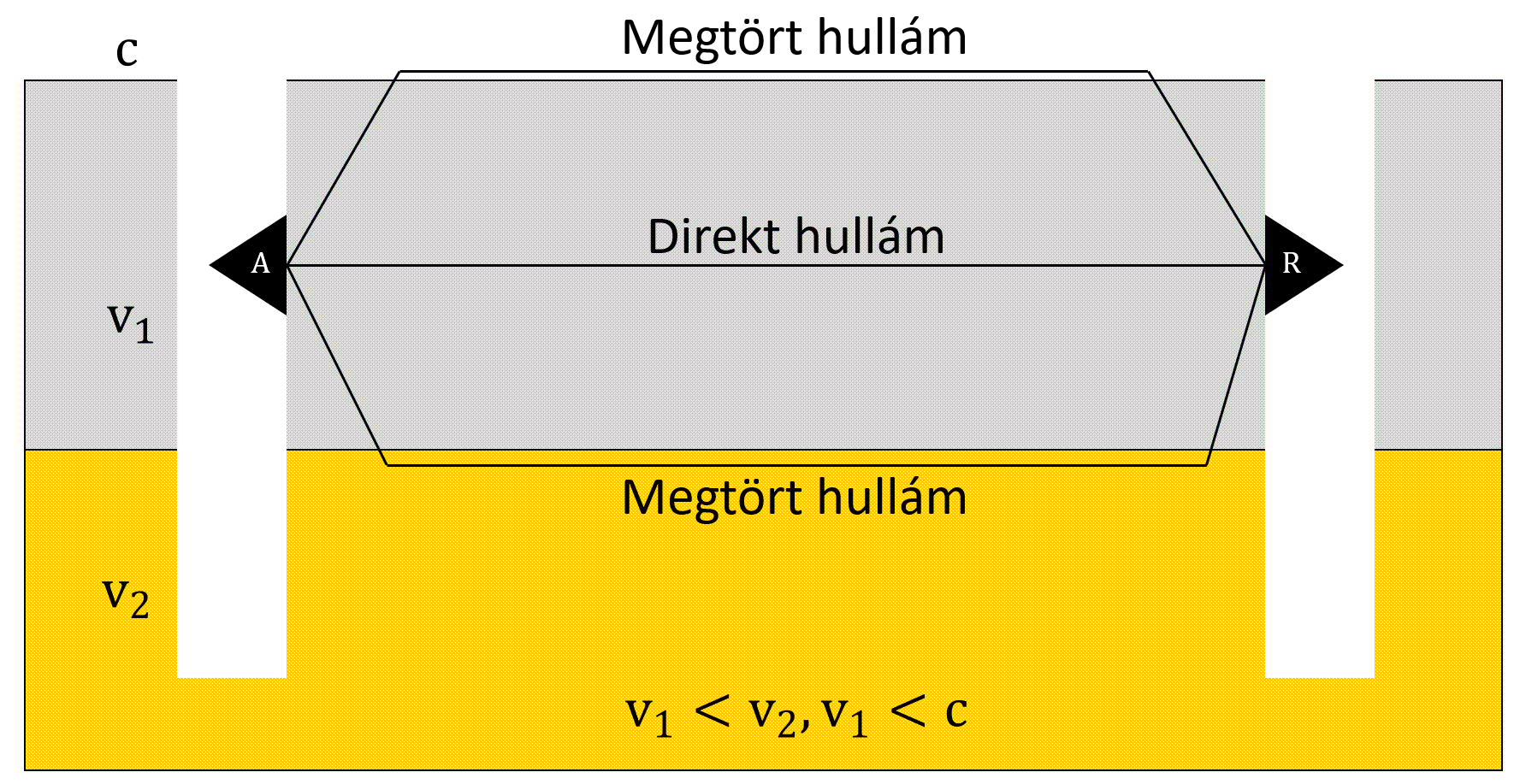
MO méréstechnika esetén az antenna távolság és a talajhullám behatolási ideje között lineáris korreláció van, ezért a terjedési sebesség a talajhullám jel meredekségéből könnyen meghatározható (3. ábra, fekete vonal) [63], [13]. Az MO méréstípus ugyanakkor időigényes, így a nagyterületen való SWC térképezés ezzel nem praktikus. Az FO méréstípus esetén, amennyiben megfelelő az antenna távolság, akkor a talajhullám a levegőhullámtól elkülöníthető. Ezért a talajhullám sebessége ( \( v_{soil,g} \) ) minden FO mérésnél meghatározható, az antenna távolság (s), valamint a talajhullám (tGW) és a levegőhullám érkezési idejének (tAW) és felhasználásával [61] alapján:
\[ v_{soil,g} = \frac{cs}{c(t_{GW}-t_{AW})+s} \]
ahol: \( v_{soil,g} \) talajhullám sebessége, \( t_{GW} \) : talajhullám érkezési ideje,\( t_{AW} \) : levegőhullám érkezési ideje, s: antenna távolság.
 |
A talajhullám-módszer hatékony felhasználásához [60], [61] a két mérési technika kombinált alkalmazását javasolta az SWC eredményes meghatározásához, amely a következő 3 lépést jelenti:
- Különböző antenna-távolságára becsült talajhullám futási idejével meghatározása többtávolság (MO) alapú módszerrel.
- MO-mérés (WARR vagy CMP) segítségével megfelelő antennatávolság kialakítása a földi és légi hullámok elkülönítésére, és
- az FO mérés adaptálása a fent említett antennatávolság alkalmazásával, a nagy területen történő adatgyűjtéshez, a talajhullám futási idejének változása, valamint a talaj dielektromos állandójában történő változás közötti kapcsolat felállítása [1] (majd SWC eloszlás térkép létrehozása). Ezt a megközelítést számos más tanulmány is igazolta [63], [64], [62], [65], [10].
A módszer előnye, hogy csak magát a talajhullámot kell értelmezni a GPR adatai alapján, de a visszaverődő felület előzetes ismerete nem szükséges.
A módszer hátrányai: csekély behatolási mélység; talajhullámok gyorsan csillapodnak, és érzékenyek a zajhullámokra, ami a mért adatok értelmezést nehezíti. A talajkondíciók (talajtípusok) és a radarbeállítások tovább korlátozhatják a rendszert gyakorlati szempontból. [10] kedvezőtlen eredményeket kapott a módszer agyagban gazdag talaj esetén való alkalmazásánál, míg [66] pedig az útpályaszerkezetek esetén történő nedvességtartalom kiértékelésénél kapott megbízhatatlan eredményeket.
Fúrólyuk GPR módszer
A fúrólyuk GPR mérés kivitelezése egy vagy két fúrólyuk segítségével történik, amelyekben az adó és vevőantennák elhelyezkednek. Hagyományosan a vevő által több pozícióból befogott direkt hullámok futási idejét használják a fúrólyukak közötti terjedési sebesség-eloszlás meghatározásához. A fúrólyukak közötti távolságok ismertek. Ezeket a sebességeket dielektromos állandóvá és talajnedvességé konvertálják a (13) és (3) egyenletek szerint.
A fúrólyuk GPR-ek esetén alkalmazott méréstechnikák (ZOP, MOP, VRP mérés), melyek bemutatását a GPR antenna rendszer és mérés technikák c. fejezetben megtettük, lehetőséget adnak, hogy az SWC eloszlást tudjunk a fúrólyukak körül és között meghatározni. ZOP esetén a direkt hullámok futási idejét, valamint a két fúrólyuk közötti ismert távolságot felhasználva számolják az átlagos terjedési sebesség profilt, amit pedig az 1D-s SWC profil meghatározásához használnak két fúrólyuk között [67]. A MOP méréstechnika esetén először a direkt hullámok futási idejét felhasználva a terjedési sebesség profil 2D-s tomográfiai képét hozzák létre [67], [68], amiből az SWC eloszlás térképet készítik el két fúrólyuk között. A VRP méréstechnika esetén az antenna helyzete és a direkt hullám érkezési ideje használatos az intervallum-sebesség meghatározására a mélységgel, így a fúrólyuk körüli SWC könnyen számítható.
A fúrólyuk GPR méréstechnika magasabb felbontást és nagyobb feltárási mélységet (pár 10 méteres) biztosít, mint a föld- vagy levegőkapcsolt megoldások. Emellett akár az SWC horizontális eloszlását is meg lehet vele határozni, amennyiben a fúrólyuk maga is horizontális kivitelezésű [65], [69]. A fúrólyukas GPR esetén jelentős probléma a direkt hullám futási idejének pontos meghatározása. [13] rámutatott, hogy a módszer a környező talajra nézve destruktív, és a mérés maga a két fúrólyuk közé (ZOP, MOP), vagy köré (VRP) korlátozódik. A 2D és 3D SWC tomográfia alkalmatlan az erősen dinamikus hidrológiai körülmények között, mivel néhány esemény az időigényes adatgyűjtési folyamat alatt következik be.
 |
Felületi visszaverődésen alapuló módszer
Levegőkapcsolt GPR segítségével mono, vagy bisztatikus konfigurációt valósít meg. A GPR antennák a felszín felett vannak bizonyos magasságban, valamely járműre rögzítve [13]. A módszer először a levegő és a földfelszín között a reflexiós koefficienst határozza meg [23], majd ezután a talaj dielektromos állandóját és végül az SWC-t.
A levegő, felszín érintkezési felületre a következő egyenlettel lehet kifejezni a reflexiós koefficienst:
\[ R=\frac{\sqrt{ε_{air}}-\sqrt{ε_{soil}}}{\sqrt{ε_{air}}+\sqrt{ε_{soil}}}=\frac{1-\sqrt{ε_{soil}}}{1+\sqrt{ε_{soil}}} \]
\( ε_{soil} \) a (21) egyenletből fakadóan R ismeretében közvetlenül meghatározható. R pedig a (22) egyenlettel számítható, a talajfelszín visszaverődés amplitudójának (A) és egy tökéletes vezető lapról való visszaverődés amplitudójának (APEC) (nagyobb, mint a radarantenna észlelési hatóköre, amelyet GPR-rel mértek azonos magasságban) felhasználásával, az alábbiak szerint:
\[ R=-\frac{A}{A_{PEC }} \]
Ezért a dielektromos állandó a következő módon fejezhető ki [70], [71] [23].
\[ ε_{soil}=(\frac{1+\frac{A}{A_{PEC}}}{1-\frac{A}{A_{A_{PEC}}}})^{2} \]
Ezt követően az SWC meghatározása Topp egyenlettel történik (lásd 3. egyenlet) a (23) egyenletben meghatározott \( ε_{soil} \) felhasználásával.
A reflexiós koefficiens érzékenyebb a talajnedvesség-változásra alacsonyabb nedvességtartalom esetén [13].
A „radarlábnyom”, vagyis az említett radarantenna észlelési hatóköre az első ú.n. Fresnel zóna átmérőjével (FZD) becsülhető:
\[ FZD= (\frac{λ^{2}}{4}+2hλ)^{0,5}\]
ahol λ: hullámhossz (c/f a levegő esetén) a GPR antenna középfrekvenciáján, h: az antenna föld feletti magassága [13].
A (24) összefüggés alapján, 1 GHz-es, a felszín felett 1 méteres magasságban működő antenna esetén 0,79 x 0,79 kalibrációs „radarlábnyomot” javasol, míg ugyanebben a magasságban, egy 225 MHz-es antenna esetén 1,76×1,76-ost.
Serbin és Or 2003, Ardekani 2013 [26], [72] kutatásai alapján ezzel a módszerrel csupán kb. 1-2 cm a behatolási mélység, amelyben SWC értéke meghatározható, azonban [13] 20 cm-es feltárást közöl.
A mérés pontossága alapvetően a befogott jel amplitúdóján múlik. A mért amplitúdókban fellépő csupán 1%-os hiba, már jelentős hibát ±0,02 m3 m-3 jelent 0,30 m3 m-3 talajnedvesség-tartalom esetén [70]. Az amplitúdón túl a felszín érdessége az antenna frekvencia és magasság, valamint a talajnedvesség mélységgel való változása is meghatározó, ugyanakkor ezekkel a tényezőkkel a (23) egyenlet nem számol [70], [13], [26], [23].
A felületi visszaverődésen alapuló módszert összefoglalva elmondható, hogy gyors az adatgyűjtési lehetőség, relatíve egyszerű a módszerkivitelezés és teljes a roncsolásmentesség, hiszen mérés alatt nem érintkezik az eszköz a felülettel [73], [18]. A módszer hátránya a limitált mélység, és a felszínérdességre és vegetációra való érzékenység. Megjegyzendő továbbá, hogy alacsony talajnedvesség-értékek esetén ez a technika kifejezetten érzékeny a talajnedvesség-változásra.
Összefoglalás
A cikk során áttekintettük a GPR-ek, mint roncsolásmentes rendszerek működésének alapelveit, valamint helyét és szerepét a talajnedvesség-meghatározásban. Kiemeltük, hogy a rugalmas pályaszerkezet sérüléseinek – melyek sok esetben a felszínről közvetlenül nem észlelhetők – és korai tönkremenetelének elsődleges forrása a hézagokon és csatlakozási pontokon beszivárgó feles vízmennyiség. A GPR rendszerek előnye, hogy a hagyományos módszerekkel szemben az úthálózatok rövidebb idő alatt ellenőrizhetőek, és roncsolásmentes műszerként lehetővé teszik a pályaszerkezetek állapotának, a földmű minőségének, ill. nedvesség okozta pályaszerkezeti károknak a kiértékelését, így az eljárás a pályaszerkezet felső felületén alapvetően láthatatlan súlyos károk megelőzésében jelenthet megoldást. Mindez a döntéstámogatást és a fenntartási alapok leghatékonyabb kezelését teszi lehetővé.
A cikkeben a 7 konkrét módszer közül négyet mutattunk be részletesebben. Hardver tekintetében talajkapcsolt GPR-t használnak a következő módszerek: visszaverthullám-módszer, talajhullám- módszer, frekvencia eltolás és az átlagos burkológörbe amplitúdója. A vizsgálat során az eszköz érintkezik a talajjal, így csak a felszín alatt jelent roncsolásmentességet. A talaj felületének érdessége, a vegetáció, és adott esetben akadályok az antenna áthelyezésekor azok a tényezők, amik az adatminőséget befolyásolják. Ezen módszereknél az elektromágneses hullám direktben áthalad a teljes talajprofilon, és nem konkrétan egy kiválasztott talajrétegre irányul, ezért, ha az SWC-t intervallumokra, rétegekre akarjuk meghatározni, az további plusz feladat. Talajnedvesség meghatározásához, jelentősebb mélységigény esetén, az ezt biztosító antennafrekvencia kiválasztása is szükséges [13].
A talajvisszaverődés módszer levegőkapcsolt GPR antennát használ, amely teljes roncsolásmentességet biztosít, azonban néhány centiméterre szűkül a feltárási mélység, és a növényborítottságra is érzékeny ez a megoldás. Az FWI módszer szintén levegőkapcsolt GPR-t használ, a pontosság növelésére alkalmazható, valamint a felszínivisszaverődés módszer okozta kalibrációs szükséglet elkerülésére [2].
A használt jelattribútumokhoz a visszavert hullám, a talajhullám és a fúrólyuk GPR módszerek a jel kétirányú futási idejét használják az átlagos hullámterjedési-sebesség kiszámításához; a felületi reflexiós módszer a levegő és a talaj felszíne közötti határfelületről való visszaverődés amplitúdóit veszi igénybe a visszaverődési együttható kiszámításához.
A műszaki keretekhez a visszaverthullám, a talajhullám és a fúrólyuk módszerekhez először a rendelkezésre álló radarhullámok átlagos sebességének meghatározása szükséges, amelyet a dielektromos állandó, majd az SWC számításához használnak. A felületi reflexiós módszerrel a reflexiós együttható és a talaj dielektromos állandója között határoznak meg összefüggést, az FWI és AEA módszerekkel pedig a radarjelekből közvetlenül is meghatározható a talaj dielektromos állandója. Nyilvánvaló, hogy a hat módszer (dielektromos állandó alapú módszerek) megköveteli az összefüggést a talaj dielektromos állandójának SWC-vé alakításához, de a pontos összefüggést terepen kell kalibrálni [3], így ez a hat módszer nem biztosít gyors és pontos SWC feltérképezési lehetőséget. Összehasonlításképpen, a frekvenciaeltolásos módszer az SWC-t egyszerűen FFT (fast Fourier transformation) használatával kapja meg a radarjelekhez, és kiküszöböli a talaj dielektromos állandójából az SWC-re való átalakítás hibáit [3].
A hét módszer fejlesztéseit és alkalmazási lehetőségeit figyelembe véve a visszaverthullám, a talajhullám és a fúrólyuk módszereket fejlesztették ki korábban, és alkalmazták azokat széles körben, de jelenleg számos korlátjuk ismeretes, mint például a talajhullám gyors csillapodása és a GPR adatok nehézkes értelmezhetősége, erős függés a visszaverő felületektől, valamint helyhez kötött mérés. A felületi reflexiós és FWI-módszereket eddig elsősorban ellenőrzött körülmények között kivitelezett kutatások esetén alkalmazták, és ezek elméletei további finomításra szorulnak. A legfrissebb fejlesztések, vagyis az AEA és frekvenciaeltolás-módszerek pedig a működési eljárásuk mielőbbi pontos letisztázását igénylik az agyagban gazdag talajok vizsgálatához.
Köszönetnyilvánítás
Jelen publikáció a TKP2021-NKTA-43 azonosítószámú projekt keretében az Innovációs és Technológiai Minisztérium (jogutód: Kulturális és Innovációs Minisztérium) Nemzeti Kutatási Fejlesztési és Innovációs Alapból nyújtott támogatásával, a TKP2021-NKTA pályázati program finanszírozásában valósult meg.
Irodalomjegyzék
[1]: Tosti, F. & E. Slob. 2015: Determination, by Using GPR, of the Volumetric Water Content in Structures, Substructures, Foundations and Soil, Cham: Springer International Publishing. https://doi.org/10.1007/978-3-319-04813-0_7
[2]: Xinbo, L., Jin, C., Xihong, C., Qixin, L., Xin, C. & Xuehong, C. 2019: Measurement of soil water content using ground-penetrating radar: a review of current methods, International Journal of Digital Earth, 12:1, 95-118, https://doi.org/10.1080/17538947.2017.1412520
[3]: Steelman, C.M. & Endres, A. L. 2011: Comparison of Petrophysical Relationships for Soil Moisture Estimation using GPR Ground Waves, Vadose Zone J. 10, pp. 270-285, https://doi.org/10.2136/vzj2010.0040
[4]: Samouëlian, A., Cousin, I., Tabbagh, A. & Guy, B.R. 2005: Electrical resistivity survey in soil science: A review, Soil and Tillage Research. 83. 173-193, https://doi.org/10.1016/j.still.2004.10.004
[5]: Sheets, K. R. & Hendrickx, J. M. H. 1995: Noninvasive soil water content measurement using electromagnetic induction. Water Resources Research 31, issn: 0043-1397, https://doi.org/10.1029/95WR01949.
[6]: Hubbard, S., Grote, K. & Rubin, Y. 2002: Mapping the volumetric soil water content of a California vineyard using high-frequency GPR ground wave data. Leading Edge 25:552–559. https://doi.org/10.1190/1.1490641.
[7]: Grote, K., Hubbard, S. & Rubin, Y. 2002: GPR Monitoring of Volumetric Water Content in Soils Applied to Highway Construction and Maintenance. The Leading Edge 21 (5): 482–504. https://doi.org/10.1190/1.1481259.
[8]: Lunt, I. A., Hubbard, S. S. & Y. Rubin. 2005: Soil Moisture Content Estimation Using Ground-penetrating Radar Reflection Data. Journal of Hydrology 307 (1): 254–269. https://doi.org/10.1016/j.jhydrol.2004.10.014.
[9]: Galagedara, L. W., Parkin, G. W., Redman, P. von Bertoldi, & Endres A. L. 2005: Field Studies of the GPR Ground Wave Method for Estimating Soil Water Content During Irrigation and Drainage. Journal of Hydrology 301 (2005): 182–197. https://doi.org/10.1016/j.jhydrol.2004.06.031 .
[10]: Weihermüller, L., Huisman, J. A., Lambot, S., Herbst, M. & Vereecken, H. 2007: Mapping the Spatial Variation of Soil Water Content at the Field Scale with Different Ground Penetrating Radar Techniques. Journal of Hydrology 340: 205–216. https://doi.org/10.1016/j.jhydrol.2007.04.013.
[11]: Gerhards, H., Wollschläger, U., Yu, Q., Schiwek, P., Pan, X. & Roth, K. 2008: Continuous and simultaneous measurement of reflector depth and average soil-water content with multi channel ground-penetrating radar. Geophysics 73: J15–J23. https://doi.org/10.1190/1.2943669
[12]: Daniels, D. J. 2004: Ground Penetrating Radar: 2nd Edition. London: Institution of Electrical Engineers.
[13]: Huisman, J. A., Hubbard, S. S., Redman, J. D. & Annan, A. P. 2003a: Measuring Soil Water Content with Ground Penetrating Radar. Vadose Zone Journal 2 (4): 476–491. https://doi.org/10.2136/vzj2003.4760.
[14]: Davis, J.L. & Annan, A.P. 2002: Ground penetrating radar to measure soil water content. p. 446–463. In J.H.
[15]: Cassidy, Nigel. 2009: Electrical and Magnetic Properties of Rocks, Soils and Fluids. In book: Ground Penetrating Radar Theory and Applications, Chapter 3, 41-72.
[16]: Berthelot, C., Podborochynski, D., Saarenketo, T., Marjerison B., & Prang, C. 2010: Ground-Penetrating Radar Evaluation of Moisture and Frost across Typical Saskatchewan Road Soils, Advances in Civil Engineering, vol. 2010, Article ID 416190, 9 pages, https://doi.org/10.1155/2010/416190
[17]: Reynolds, J. M. 2011: An Introduction to Applied and Environmental Geophysics, 2nd Edition, ISBN: 978-0-471-48535-3 April 2011, Chapter 13, pp 551.
[18]: Leng, Z. & Al-Qadi, I. L. 2014: An Innovative Method for Measuring Pavement Dielectric Constant Using the Extended CMP Method with Two Air-coupled GPR Systems. NDT & E International 66: 90–98. https://doi.org/10.1016/j.ndteint.2014.05.002.
[19]: Slob, E., Sato, M. & Olhoeft, G. 2010: Surface and Borehole Ground-penetrating-radar Developments. Geophysics 75 (5): 75A103–75A120. https://doi.org/10.1190/1.3480619.
[20]: Nakashima, Y., Hui, Z., Sato, M. 2001: Estimation of groundwater level by GPR in an area with multiple ambiguous reflections, Journal of Applied Geophysics, 2001, Pages 241-249, ISSN 0926-9851, https://doi.org/10.1016/S0926-9851(01)00068-4
[21]: Mínguez, M. R. 2012: Aplicación del geo-radar 3D multifrecuencia como herramienta de alto
rendimiento para la detección de zonas de acumulación de humedad en obras lineales. Rutas
Técnica, vol. 150, 6 pp.
[22]: Hugenschmidt, J., Loser, R. 2008: Detection of chlorides and moisture in concrete structures with ground penetrating radar. Mater. Struct. 41, 785–792, https://doi.org/10.1617/s11527-007-9282-5.
[23]: Lambot, S., L. Weihermuller, J. A. Huisman, H. Vereecken, M. Vanclooster, & E. C. Slob. 2006: Analysis of Airlaunched Ground-penetrating Radar Techniques to Measure the Soil Surface Water Content. Water Resources Research 42, W1140311, https://doi.org/10.1029/2006WR005097.
[24]: Benedetto, A. & Pensa, S. 2007: Indirect diagnosis of pavement structural damages using surface GPR reflection techniques. Journal of Applied Geophysics. 62. 107-123, https://doi.org/10.1016/j.jappgeo.2006.09.001.
[25]: Sybilski, D., Wojciech, B., Jacek, S. & Krysinski, L. 2012: Reasons of Premature Cracking Pavement Deterioration – A Case Study. 4. 1029-1038, https://doi.org/10.1007/978-94-007-4566-7_98
[26]: Serbin, G. & Or, D. 2003: Near-Surface Soil Water Content Measurements Using Horn Antenna Radar. Vadose Zone Journal 2 (4): 500–510. https://doi.org/10.2136/vzj2003.5000.
[27]: Topp, G. C., Davis, J. L. & Annan, A. P. 1980: Electromagnetic Determination of Soil Water Content: Measurements in Coaxial Transmission Lines. Water Resources Research 16 (3): 574–582. https://doi.org/10.1029/WR016i003p00574.
[28]: Nadler, A., Dasberg, S. & Lapid, I. 1991: Time domain reflectometry measurements of water content and electrical conductivity of layered soil columns. Soil Sci. Soc. Am. J. 55:938–943. https://doi.org/10.2136/sssaj1991.03615995005500040007x
[29]: Roth, C.H., Malicki, M.A. & Plagge, R. 1992: Empirical evaluation of the relationship between soil dielectric constant and volumetric water content as the basis for calibrating soil moisture measurements by TDR. J. Soil Sci. 43:1–13. Hydraulic Properties.” Advances in Water Resources 54 (2013): 38–56, https://doi.org/10.1111/j.1365-2389.1992.tb00115.x.
[30]: Jacobsen, O.H., & Schjønning, P. 1993: A laboratory calibration of time domain reflectometry for soil water measurements including effects of bulk density and texture. J. Hydrol. 151:147–157. https://doi.org/10.1016/0022-1694(93)90233-Y
[31]: Malicki, M.A., Plagge, R. & Roth, C.H. 1996: Improving the calibration of dielectric TDR soil moisture determination taking into account the solid soil. Eur. J. Soil Sci. 47:357–366. https://doi.org/10.1111/j.1365-2389.1996.tb01409.x.
[32]: Curtis, J.O. 2001: Moisture effects on the dielectric properties of soils. IEEE Trans. Geosci. Remote Sens. 39:125–128.
[33]: Birchak, J.R., Gardner, C.G., Hipp, J.E., & Victor, J.M. 1974: High dielectric constant microwave probes for sensing soil moisture. Proc. IEEE 62, 93–98.
[34]: Wharton, R.P., Rau, R.N. & Best, D.L. 1980: Electromagnetic propagation logging: Advances in technique and interpretation. Pap. 9267. In SPE Annu. Tech. Conf., Dallas, TX. 21–24 Sept. 1980. Soc. Pet. Eng., Richardson, TX. https://doi.org/10.2118/9267-MS
[35]: Dobson, M.C., Ulaby, F.T., Hallikainen, M.T. & El-Rayes, M.A. 1985: Microwave dielectric behaviour of wet soil. Part II. Dielectric mixing models. IEEE Trans. Geosci. Remote Sens. 23:35–46.
[36]: Roth, K., R. Schulin, Flu¨hler, H. & Attinger, W. 1990: Calibration of time domain reflectometry for water contentmeasurement using a composite dielectric approach. Water Resour. Res. 26:2267–2273.
[37]: Heimovaara, T.J., Bouten, W. & Verstraten, J.M. 1994: Frequency domain analysis of time-domain reflectometry waveforms: 2. A four component complex dielectric mixing model for soils. Water Resour. Res. 30, 201–209, https://doi.org/10.1029/93WR02949.
[38]: Sen, P.N., Scala, C. & Cohen, M.H. 1981: A self-similar model for sedimentary rocks with application to the dielectric constant of fused glass beads. Geophysics 46:781–795. https://doi.org/10.1190/1.1441215
[39]: Sen, P.N. 1984: Grain shape effects on dielectric and electrical properties of rocks. Geophysics 49, 586–587. https://doi.org/10.1190/1.1441695
[40]: Kenyon, W.E. 1984: Texture effects on megahertz dielectric properties of calcite rock samples. J. Appl. Phys. 55:3153–3159. https://doi.org/10.1063/1.333315
[41]: Tyč, S., Schwartz, L.M., Sen, P.N. & Wong, P. 1988: Geometrical models for the high-frequency dielectric properties of brine saturated sandstones. J. Appl. Phys. 64:2575–2582. https://doi.org/10.1063/1.341645
[42]: Endres, A.L. & Redman, J.D. 1996: Modelling the electrical properties of porous rocks and soil containing immiscible contaminants. J. Environ. Eng. Geophys. 1, 105–112. https://doi.org/10.3997/2214-4609-pdb.209.1993_004
[43]: Friedman, S.P. 1998: A saturation degree-dependent composite spheres model for describing the effective dielectric constant of unsaturated porous media”. Wat. Resour. Res. 34:2949–2961. https://doi.org/10.1029/98WR01923
[44]: Jones, S.B., & Friedman, S.P. 2000: Particle shape effect on the effective permittivity of anisotropic or isotropic media consisting of aligned or randomly oriented ellipsoidal particles. WaterResour. 36:2821–2833 Munich, Germany. https://doi.org/10.1029/2000WR900198.
[45]: Cosenza, P., Camerlynck, C. & Tabbagh, A. 2003: Differential effective medium schemes for investigating the relationship between high-frequency relative dielectric permitivity and water content of soil. Water Resour. Res. 39(9):1230. https://doi.org/10.1029/2002WR001774.
[46]: Endres, A.L., & Bertrand, E.A. 2006: A pore-size scale model for the dielectric properties of water-saturated clean rocks and soils. Geophysics 71: F185–F193. https://doi.org/10.1190/1.2360192
[47]: Chen, Y., Or, D. 2006: Geometrical factors and interfacial processes affecting complex dielectric permittivity of partially saturated porous media. Water Resour. Res. 42, W06423.
[48]: Topp, G.C., Yanuka, M., Zebchuk, W.D. & Zegelin, S.J. 1988: Determination of electrical conductivity using time domain reflectometry: Soil and water experiments in coaxial lines. Water Resour. Res. 24:945–952.
[49]: Chan, C. Y. & Knight, R. J. 1999: Determining water content and saturation from dielectric measurements in layered materials, Water resources research, Volume35, Issue1, Pages 85-93, https://doi.org/10.1029/1998WR900039
[50]: Jacobsen, O.H. & Schjønning, P. 1994: Comparison of TDR calibration functions for soil water determination. p. 9–23. In Proc. Time Domain Reflectometry, Applications in Soil Science, Research Centre Foulum, Denmark. 16 Sept. 1994. SP-Report 25-33. Danish Inst. of Plant and Soil Sci., Tjele, Denmark.
[51]: Stoffregen, H., Zenker, T. & Wessolek, G. 2002: Accuracy of Soil Water Content Measurements Using Ground Penetrating Radar: Comparison of Ground Penetrating Radar and Lysimeter Data. Journal of Hydrology 267: 201–206. https://doi.org/10.1016/j.jhydrol.2012.02.041.
[52]: Gorriti, A.G., Slob, E.C. 2005: Comparison of the different reconstruction techniques of permittivity from S-parameters. IEEE Trans. Geosci. Remote 43, 2051–2057. https://doi.org/10.1109/TGRS.2005.854312.
[53]: Herkelrath, W.N., Hamburg, S.P. & Murphy, F. 1991: Automatic, real-time monitoring of soil moisture in a remote field area with time domain reflectometry. Water Resour. Res. 27:857–864. https://doi.org/10.1029/91WR00311
[54]: Patriarca, C., Tosti, F., Velds, C., Benedetto, A., Lambot, S. & Slob, E.C. 2013: Frequency dependent electric properties of homogeneous multi-phase lossy media in the ground-penetrating radar frequency range. J. Appl. Geophys. 1(97), 81–88. https://doi.org/10.1016/j.jappgeo.2013.05.003
[55]: Fiori, A., Benedetto, A. & Romanelli, M. 2005: Application of the effective medium approximation for determining water contents through GPR in coarse-grained soil materials. Geophys. Res. Lett. 32, L09404
[56]: van Overmeeren, R. A., Sariowan, S. V. & Gehrels, J. C. 1997: Ground Penetrating Radar for Determining Volumetric Soil Water Content; Results of Comparative Measurements at Two Test Sites. Journal of Hydrology 197 (1997): 316–338. https://doi.org/10.1016/S0022-1694(96)03244-1.
[57]: Klenk, P., Jaumann S. & K. Roth. 2015: Quantitative High-resolution Observations of Soil Water Dynamics in A Complicated Architecture Using Time-lapse Ground-penetrating Radar. Hydrology and Earth System Sciences 19 (3): 1125–1139. https://doi.org/10.5194/hess-19-1125-2015, 2015.
[58]: Loeffler, O. & Bano, M. 2004: Ground Penetrating Radar Measurements in a Controlled Vadose Zone. Vadose Zone Journal 3 (4): 1082–1092. https://doi.org/10.2136/vzj2004.1082.
[59]: Garambois, S., Senechal, P. & Perroud, H. 2002: On the Use of Combined Geophysical Methods to Assess Water Content and Water Conductivity of Near-Surface Formations. Journal of Hydrology 259 (2002): 32–48. https://doi.org/10.1016/S0022-1694(01)00588-1.
[60]: Du, S. 1996: Determination of Water Content in the Subsurface with the Ground Wave of Ground Penetrating Radar. PhD diss., Ludwig-Maximilians-Universität.
[61]: Sperl, C. 1999: Determination of Spatial and Temporal Variation of the Soil Water Content in an Agro-ecosystem with Ground Penetrating Radar. PhD diss., Thechnische University München.
[62]: Grote, K., Hubbard, S. S. & Rubin, Y. 2003: Field-scale estimation of volumetric water content using GPR ground wave techniques. Wat Resour. Res. 39(11). https://doi.org/10.1029/2003WR002045.
[63]: Huisman, J. A., Snepvangers, J. J. C. Bouten, W. & Heuvelink, G. B. M. 2002: Mapping Spatial Variation in Surface Soil Water Content: Comparison of Ground-penetrating Radar and Time Domain Reflectometry. Journal of Hydrology 269 (3): 194–207, https://10.1016/S0022-1694(02)00239-1
[64]: Huisman, J. A., Snepvangers, J. J. C, Bouten, W. & Heuvelink, G. B. M. 2003: Monitoring Temporal Development of Spatial Soil Water Content Variation. Vadose Zone Journal 2 (4): 519–529. https://doi:10.2136/vzj2003.5190
[65]: Galagedara, L. W., Redman, J. D. & Endres, A. L. 2002: Temporal and Spatial Variation of Soil Water Content Measured by Borehole GPR Under Irrigation and Drainage. Paper presented at the 9th international conference on ground penetrating radar, Santa Barbara, April 29–May 2. https://doi.org/10.1117/12.462253.
[66]: Laurens, S., Balayssac, J.-P., Rhazi, J., Klysz, G., & Arliguie, G. 2005: Non-destructive evaluation of concrete moisture by GPR: experimental study and direct modeling. Mater. Struct. 38(283), 827–832. https://doi.org/10.1007/BF02481655.
[67]: Binley, A., Winship, P., Middleton, R., Pokar, M. & West, J. 2001: High-resolution Characterization of Vadose Zone Dynamics Using Cross-borehole Radar. Water Resources Research 37 (11): 2639–2652. https://doi.org/10.1029/2000WR000089.
[68]: Alumbaugh, D., Chang, P. Y., Paprocki, L., Brainard, J. R., Glass, R. J. & Rautman, C. A. 2002: Estimating Moisture Contents in the Vadose Zone Using Cross-borehole Ground Penetrating Radar: A Study of Accuracy and Repeatability. Water Resources Research 38 (130912): 45-1–45-12, https://doi.org/10.1029/2001wr000754.
[69]: Galagedara, L. W., Parkin, G. W., Redman, J. D. & Endres, A. L. 2003: Assessment of Soil Moisture Content Measured by Borehole GPR and TDR Under Transient Irrigation and Drainage. Journal of Environmental & Engineering Geophysics 8 (2): 77–86. https://doi.org/10.4133/JEEG8.2.77.
[70]: Redman, J.D., Davis, J.L. Galagedara, L.W. & Parkin, G.W. 2002: Field studies of GPR air launched surface reflectivity measurements of soil water content. Proc. of the Ninth Conf. on Ground Penetrating Radar. Proc. SPIE 4758:156–161. https://doi.org/10.1117/12.462256.
[71]: Maser, K. R., & Scullion, T. 1992: Automated Pavement Subsurface Profiling Using Radar: Case Studies of Four Experimental Field Sites. Transportation Research Record 1344: 148–54.
[72]: Serbin, G., & Or, D. 2004: Ground-penetrating Radar Measurement of Soil Water Content Dynamics Using a Suspended Horn Antenna. IEEE Transactions on Geoscience & Remote Sensing 42 (9): 1695–1705, https://doi.org/10.1109/TGRS.2004.835790
[73]: Ardekani, M. R. M. 2013: Off- and On-ground GPR Techniques for Field-scale Soil Moisture Mapping. Geoderma 200–201 (2013): 55–66, https://doi.org/10.1016/j.geoderma.2013.02.010.
Erre a szövegre így hivatkozhat:
Herceg András: Földradar (GPR) alapú talajnedvességtartalom-mérési lehetőségek földművek esetén – szakirodalmi áttekintés, 2022, DOI: 10.36246/UL.2022.1.03
