https://doi.org/10.36246/UL.2023.1.06
2023; 11. évfolyam, 17. szám
Bevezetés
Magyarországon az útpályaszerkezet megerősítésnek méretezése MSZ [1] szabvány szerinti billenőkaros behajlásmérő eszközzel mért behajláson alapul. A mérés időpontja szerint a mért behajlást – homogén útszakaszonként – az évszaki szorzó [2] (é) segítségével talajcsoportonként a mértékadó hónapra átszámítjuk.
Az évszaki szorzók talajcsoportonkénti értékének meghatározása országos un. etalon szakaszokon március –november hónapokban végzett folyamatos mérések segítségével történt [3].
A mérési eredmények nagyon nagy szórást mutattak, sőt az április és május hónapra „elvárt” legnagyobb behajlás egyes esetekben, főleg kötött talajok esetén augusztus hónapra esett. Agyag altalaj egy adott megyében 27 db etalon szakaszon a behajlásból számított havi szorzók minimum, maximum értékei egy adott évben mérve:
| Hónap | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Minimum | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,15 | 1,20 |
| Maximum | 2,38 | 1,67 | 2,46 | 1,90 | 2,84 | 1,99 | 1,76 | 2,46 | 2,74 |
Egy homogén szakaszra vonatkozóan a havi szorzó meghatározása úgy történt, hogy a legnagyobb behajlást eredményező hónapban mért behajlás értékét osztották az adott havi behajlás értékével. Az 1,00 értéket akkor kapjuk, ha abban a hónapban volt a mért legnagyobb behajlás.
Az 1. táblázat jól szemlélteti az évszaki szorzó alkalmazásában rejlő rendkívül nagy bizonytalanságot, még abban a kivételes esetben is, amikor minden hónapban mérünk behajlást.
Egy konkrét útszakaszon nem ismerjük a valós évszaki szorzót. Kötött talaj esetén a helyes évszaki szorzó értéke 1,00 – 2,84 között valószínű. Átmeneti talajoknál is hasonló eredményekre jutunk.
Azt gondolhatnánk, hogy homoktalajok esetén az eredmények lényegesen kedvezőbbek, de a 2. táblázatban a mérési eredmények ezt nem igazolják.
| Hónap | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Minimum | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 |
| Maximum | 2,06 | 2,29 | 2,63 | 2,28 | 2,37 | 2,01 | 1,92 | 1,78 |
A jelenleg használt évszaki szorzók talajcsoportonként országos átlagot reprezentálnak, de a pályaszerkezet méretezéskor adott útszakaszon kell ezeket használni, ahol az országos átlag használata teljesen megbízhatatlan, rendkívül pontatlan. A pontatlanság következtében a pályaszerkezet méretezése vezethet túlméretezéshez, vagy alul méretezéshez. Mindkét eset jelentős nemzetgazdasági veszteséget okoz. A túlméretezésből eredő veszteség nem kompenzálja az alulméretezésből származó veszteséget, hanem növeli, ebből következően az évszaki szorzó pontosítása jelentős nemzetgazdasági érdek.
A probléma már a 1980-as évek végén is közismert volt [3], de az évszaki szorzók megbízható meghatározására a mai napig nem került sor annak ellenére, hogy az ejtősúlyos teherbírásmérő készülék által mért behajlási teknők adatai már több mint két évtizede rendelkezésre állnak.
A tanulmány célja adott homogén útszakaszra vonatkozó, a teherbírásmérés időpontjára jellemző évszaki szorzók megbízható számítása a mért behajlási teknők segítségével.
Dinamikus behajlásmérés eredményének átszámítása statikus behajlásra a jelenlegi gyakorlat szerint
Hazánkban kétféle típusú készülék mér behajlási teknőt, az FDW típusú ejtősúlyos berendezések – a KUAB-ok és Dynatest készülékek és a gördülőkerekes Curviometer. A Magyar Közút üzemeltetésben lévő KUAB-ok 1200 mm-es behajlási teknőt mérnek ~20-25 ms teherfelhordási idővel, hasonló a Dynatest teherfelhordási ideje is. A Colas tulajdonában lévő eszköz teherfelhordási ideje ettől eltérő.
A Curviométer mérési sebessége ~18 km/h.
Az ugyancsak használatos Lacroix jelenleg csak legnagyobb behajlást mér – a behajlási teknő mérésére alkalmassá lehetne tenni -, mérési sebessége 3-4 km/h.
A továbbiakban elsősorban a 20-25 ms teherfelhordási idejű készülékekkel foglalkozom, mivel ez felel meg az e-UT 09.02.31:1998 „Dinamikus teherbírásmérés” UME előírásnak, és az ilyen készülékkel mért dinamikus teherbírás mérés eredménye számítható át az e-UT 09.02.34 UME szerint statikus behajlás értékre.
Az átszámítás a KUAB és az MSZ 2509/4-1989 szerinti billenőkaros mérés összeméréséből származik, 1998.-ban az összefüggés a következő volt:
\[ S_{stat}=1,37\ S_{din}-0,19 \]
\[ S_{din}=\ d_oc_{F\ }c_T \]
\[ c_F=50\ 000/F \]
\[ c_T=1,3-0,015\ T_B \]
ahol
\( d_o \) – a terhelő tárcsa tengelyében mért dinamikus behajlás (mm)
\( F \) – terhelő erő (N)
\( c_F \) – kerékterhelési korrekciós tényező
\( c_T \) – hőmérsékleti korrekcios tényező
\( T_B \) – a burkolat felületének hőmérséklete (oC)
\( S_{stat} \) – számított statikus behajlás (mm)
Az összehasonlító mérés regressziója R2=0,925 volt.
- évtől az (1) összefüggést megváltoztatták, mivel kis behajlások esetén az (1) negatív eredményt adott, ami irreális. Az új összefüggés:
\[ S_{stat}=1,2\ S_{din}-0,08 \]
Az (1) és (5) lineáris összefüggés elméletig csak és kizárólag, akkor lehet helyes, ha a vizsgált pályaszerkezeti rétegek rugalmassági modulusa szinte teljesen azonos arányban változik a teherfelhordás sebességének függvényében.
Az állítás igazsága bizonyítható Love [4] és Burmister [5] egyenleteinek felhasználásával készült programokkal, pl. BISAR, ALIZE stb.
Ha minden réteg rugalmassági modulusának változása azonos a teherfelhordás sebességének függvényében, akkor az összehasonlító vizsgálat során az (1) és (5) összefüggésben nem szerepelhetne konstans érték. A konstansok azért szerepelnek az (1) és (5) képletekben, mivel az összemérések során így kapták a jobb korrelációt, de ennek nincs elméleti alapja.
Bár tudjuk, hogy a pályaszerkezeti rétegek rugalmassági modulusának változása a teherfelhordási idő függvényében nem teljesen azonos, de a gyakorlatban előforduló hőmérséklet és teherfelhordási idő tartományban közel azonos. USA Virginia államában több eltérő típusú pályaszerkezetben 2000. május – 2000. július között mérték [6] a pályaszerkezeti rétegekben keletkező feszültségeket.
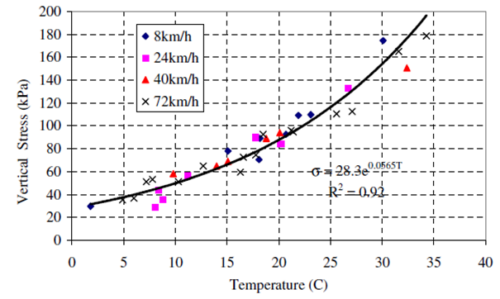 |
A nyomás mérése közvetlenül az aszfaltréteg alatt történt.
A mérési eredményekből az következik (1. ábra), hogy a pályaszerkezeti rétegekben kialakult feszültségek sokkal inkább függetlenek a terhelés sebességétől, a teherfelhordás idejétől, mintha azzal a feltételezéssel élnénk, hogy ettől függenek.
Amennyiben feltételezzük, hogy a kialakult feszültségek függetlenek a terhelési időtől, akkor szükségképpen azt is feltételezzük, hogy a terhelési idők aránya azonosan hat a pályaszerkezeti rétegek rugalmassági modulusainak változási arányára, vagyis ha pl. az aszfaltréteg rugalmassági modulusa a terhelési idő növelése miatt „k” értékkel csökken, akkor minden egyes további pályaszerkezeti réteg pl. altalaj rugalmassági modulusa is közel azonos „k” értékkel csökken, miközben a terhelés hatására a pályaszerkezetben keletkező feszültségek változatlanok maradnak.
Ellenkező esetben, ha a hidraulikus kötésű útalapok vagy mechanikai stabilizációk, ill. az altalajok rugalmassági modulusainak változása az aszfalt rugalmassági modulusának változásának arányától/hányadosától jelentősen eltérne, akkor a számított 2 sokkal rosszabb lenne, sőt alig lenne regresszió.
Természetesen változatlan feszültség és arányosan csökkenő rugalmassági modulus mellett a fajlagos megnyúlások fordítottan arányosan növekednek, így a teljes összenyomódás, a behajlási teknő is fordítottan arányosan növekszik.
Az évszaki szorzó megbízható számításához először a billenőkaros és a dinamikus mérés közötti „ ” érték meghatározása szükséges, ahol \( E_{stat}=kE_{din} \) minden pályaszerkezeti rétegre.
Dinamikus behajlásmérés eredményének átszámítása statikus behajlásra a pálya-szerkezeti rétegek rugalmassági modulusainak ismeretében
A dinamikus teherbírásmérés KUAB, Dynatest készülékek által mért behajlási teknőkből a kereskedelmi forgalomban elérhető visszaszámoló programok segítségével, ALIZE, EVERCALC stb. lehetséges a pályaszerkezeti rétegek rugalmassági modulusainak számítása.
A programok használata során általában következő feltételekkel élünk:
- minden réteg homogén, izotrop,
- a rétegek lineárisan rugalmasan viselkednek az igénybevételi tartományban,
- a rétegek vízszintesen legalább 2,5 méterig terjednek,
- a rétegenkénti „ ” Poisson-szám nem változik,
- a rétegek vastagsága állandó,
- az alsó réteg egy végtelen féltér, vagy egy adott mélységig terjed, amely alatt a végtelen féltér már összenyomhatatlan.
A programok többsége csak kör alakú rugalmas terhelő tárcsát tud kezelni, amely tárcsa alatt egyenletes a feszültségeloszlás, mivel Love [4] ezekre a feltételre oldotta meg a differenciálegyenletet.
Love egyenleteinek felhasználásával oldotta meg Burmister [5] a többrétegű rendszereket.
Mint minden modell így a pályaszerkezetben keletkező feszültségeket és alakváltozásokat számoló programok is csak megközelítik a valóságot. A modell és valóság általában a feltételek hiányos teljesülése miatt tér el egymástól. Az a-f feltételek közül mindegyikről állíthatjuk, hogy csak korlátozottan teljesül. Ez különösen igaz akkor, amikor nem egy ponton mérünk, hanem egy homogén szakaszt vizsgálunk.
Homogén szakasz esetén elvárjuk, hogy a mért behajlások szórása/átlaga, relatív szórása 0,5 alatt maradjon.
Külön ki kell emelni a b. feltételt, mely szerint a pályaszerkezeti rétegek rugalmasan viselkednek, ami gyakorlatilag azt jelenti, hogy tehermentesítés után nincs mérhető tartós alakváltozás, deformáció.
A billenőkaros behajlásmérés esetén ezt nem kell külön igazolni, hiszen a mérés sajátsága, hogy rugalmas visszaalakulást mér. A rugalmas visszaalakulás értéke független attól, hogy esetleg méréskor a terhelő gépkocsi gumiabroncsának a lenyomata megjelenik a burkolat felületén, ami egyértelmű jele a tartós alakváltozásnak, deformációnak.
Dinamikus mérések esetén a teljes összenyomódást mérjük, amelyben benne van az aszfaltrétegek lineáris viszkoelasztikus tulajdonsága miatti tartós alakváltozás is. A dinamikus mérések pontossága \( \pm0,002\ mm \). A mért behajlási teknőt érdemben az ennél nagyobb tartós alakváltozás befolyásolná. A dinamikus mérés jellemzi az egységtengely áthaladást, ha tehát egy egységtengely áthaladás 0,002 mm tartós alakváltozást okozna, akkor már az „A” forgalmi terhelésnek megfelelő 10 000 egységtengely áthaladás esetén 20 mm lenne a nyomvályú.
A tapasztalat egyértelműen az, hogy a pályaszerkezetben keletkező tartós alakváltozás nem befolyásolja a mért behajlási teknőt, a tartós alakváltozás a mérési pontosságnál lényegesen kisebb. Így a pályaszerkezet lineárisan rugalmas viselkedésének feltételezése nem hiba, ha a mérést 4-72 km/h sebességgel, vagy ennek megfelelő terhelési idővel végezzük 30 oC-ot nem meghaladó aszfalt-pályaszerkezeti hőmérsékleten. A hőmérsékletet nem a burkolat felületére, hanem rétegenként a rétegvastagságok közepére vonatkoztatva értelmezzük.
A lineárisan rugalmas viselkedés feltételezése közelítés, néhány program lineáris viszkoelasztikus viselkedést is figyelembe tud venni, ez különösen az aszfaltrétegek esetén lehet fontos, ahol a viselkedés viszkoelasztikus. A lineárisan rugalmas és a lineáris viszkoelasztikus modell közötti fő eltérés, hogy utóbbi esetén állandó feszültség mellett a fajlagos alakváltozás az idő függvényében változó. Azonban mindkét esetben igaz, hogy a feszültség arányos a fajlagos alakváltozással.
Abban az esetben, ha a deformációt, tartós alakváltozást is figyelembe akarjuk venni, akkor nemlineáris viszkoelasztikus modellekkel célszerű számolni, különösen nyári melegben, ha a teherfelhordás sebessége, a terhelés frekvenciája alacsony, pl. csomópontokban álló járművek ill. forgalmi torlódás miatti sebességcsökkenés esetén.
A helyszíni teherbírásmérést minden esetben 50 000 N terhelésre számítjuk, akár dinamikus, akár statikus billenőkaros vagy gördülőkerekes mérésről van szó. A dinamikus FDW méréseknél az 50 000 N terhelésen kívül más egyéb számottevő terhelés nem éri a mérőpontot.
Más a helyzet a gördülőkerekes és billenőkaros méréseknél. A mérések sajátságának megfelelően (2. ábra) a terhelést adó tehergépkocsi hátsó tengelyén lévő mindkét ikerabroncsáról jut terhelés a mérőpontokra.
Billenőkaros mérés esetén az ikerabroncsok terhelését figyelembe kell venni a mérőcsúcsnál, 1500 mm, és 2500 mm-re a billenőkaros mérőkészülék lábainál. A szakirodalomban a billenőkaros mérésekre BB mérésként szoktak hivatkozni, pedig jelentős az eltérés az országonként használt készülékek kialakításában, így a mért legnagyobb behajlás értéke is különbözik a készülék típusától függően.
 |
A hazai szabványos készüléknél még figyelembe kell venni, hogy a készülék 1200 mm-nél billen, fordul el. A tényleges mérés a mérőcsúcs és az 1200 mm-re lévő fordulópont között történik (3. ábra.), így kapjuk a behajlási értéket.
Az eltérő mérési módszerek esetén kapott behajlási teknőket (3. ábra) félig merev pályaszerkezeten mutatom be, ahol a 3. táblázat szerinti pályaszerkezeti rétegek kedvezőtlenül nem dolgoznak együtt.
 |
Az UME szerint mért dinamikus behajlási teknőből visszaszámított rétegenkénti rugalmassági modulusok és a statikus rugalmassági modulusok közötti arány saját méréseink és számításaink szerint 1,71.
| Rugalmassági modulus (Mpa) | ||||
| Vastagság (mm) | Réteg típusa | Dinamikus | Statikus | |
| 145 | aszfalt | 2100 | 1228 | |
| 150 | Ckt-4 | 1200 | 702 | |
| 200 | Cth-2 | 650 | 380 | |
| altalaj | 174 | 102 | ||
A 3. ábrán az ikerkerekek által okozott behajlási teknőt a 3. táblázat szerinti statikus rugalmassági modulusokkal számoltam, figyelembe véve a szomszédos ikerkerék terhelését is. Az ikerkerék „kamion” nyerges vontató és a nehéz tehergépkocsi által okozott behajlási teknők azért térnek el egymástól, mivel az ikerabroncsok alatt kialakult keréklenyomatok, a terhelési felületek és a feszültségeloszlások is különbözőek.
Az ikerabroncs által okozott behajlási teknő számításánál azt is figyelembe kell venni, hogy a feszültségeloszlás a gumiabroncs alatt nem egyenletes [6].
Nyerges vontató esetén a kerék szélessége 315 mm, míg tgk. esetén 200 mm, az abroncsnyomás 0,8 MPa, míg tgk. esetén 0,6 MPa. A szélesebb abroncs azonos terhelésnél kisebb behajlást eredményez, viszont nagyobb függőleges feszültségeket okoz, ami növeli a deformációt, a nyomvályú kialakulásának sebességét.
A billenőkaros behajlásmérő minden esetben a terhelés hatására létrejött behajlási teknőben mér, így a mért behajlás függ a behajlási teknő alakjától, ami pedig függ a pályaszerkezet felépítésétől.
A kérdés, hogy az eltérő behajlási teknők milyen mértékben befolyásolják a mért billenőkaros behajlást.
A k =1,71 arányt 2022. évi mérésekből határoztam meg. A 22. j. főúton a KUAB készülékkel mértünk 25 ms terherfelhordási idővel és max. 1200 mm méretű behajlási teknővel (4. ábra), a 451. j. főúton Dynatest készülékkel mértünk, ahol a behajlási teknő 1800 mm (5. ábra). A mért szakaszokon félig merev, hajlékony pályaszerkezetek fordultak elő, nagyon vegyes pályaszerkezettel.
A dinamikus behajlásból hőmérsékleti korrekció nélkül számítottuk az (5) szerinti szabványos behajlást, amit összehasonlítottunk a „k” tényezővel számolt statikus rugalmassági modulusok segítségével számolt \( S_{BB} \) billenőkaros behajlással, ahol a nyerges vontató ikerkerék terhelését vettük alapul.
 |
 |
Az altalaj teherbírását az 1200 mm, 1500 mm, és 1800 mm távolságban lévő mért érték segítségével pontosítottuk. Az altalaj teherbírási értékét, akkor fogadtuk el, ha a mért és számított behajlás értéke a mérési pontosságon belülre esik \( \pm0,002\ mm \).
Az 1200 mm behajlási teknő esetén ez nem lehetséges, ekkor a 900 mm és az 1200 mm az alapja az altalaj teherbírásának, de ebben az esetben az RMS%<1,5 % a feltétel.
A „k” tényezőt budapesti munkáknál is ellenőriztük, ami megerősítette az 1,71 értékű „k” tényező helyességét.
A statikus rugalmassági modulusok és az ikerkerék terhelése alapján (2. ábra) számíthatjuk a statikus behajlási teknőt és a legnagyobb behajláshoz tartozó \( S_{BB} \) behajlást (3. ábra).
Az útszakaszra jellemző altalaj talajcsoportjának ismeretében az e-UT 06.03.13:2005 5.1 táblázata alapján felvett talaj teherbírási modulussal ismételten számítjuk a billenőkaros behajlás mértékadó értékét. A két behajlás értékének hányadosa (6. ábra) adja az évszaki szorzót.
 |
\[ c_{é}=\frac{S_{BBM}}{S_{BB}} \]
A 3. táblázatban szereplő szakaszon az \( S_{BB}=0,382\ mm \), \( S_{BBm}=0,722\ mm, cé=1,89 \)
A 451. j. főúton a számított évszaki szorzók 1,39- 2,3 között változtak, a legkisebb évszaki szorzót ott kaptuk, ahol az út mellett közvetlenül vizes terület van. Itt a mért dinamikus talajteherbírás csupán 59 MPa, ami statikusan 35 MPa-t jelent, ezen a szakaszon a rendkívüli szárazság ellenére az altalaj a mértékadó teherbírás közelében volt.
A számított évszaki szorzók értékei jelentősen meghaladják az e-UT 06.03.13:2005 7.1 táblázatában megadott maximumot, de az 1. táblázat 1987. évben ténylegesen mért etalon szakaszok értékein belül maradnak annak ellenére, hogy a 2022. év rendkívül aszályos volt.
Az altalaj pillanatnyi víztartalma nemcsak a korábban lehullott csapadék mennyiségétől függ, hanem számtalan tényező mellett a talajvíz szintje és az altalaj talajcsoportja is befolyásolja. Természetesen a vízgyűjtőre lehullott csapadék, a folyók távolsága hat a talajvíz szintjére, az összefüggések azonban sokkal bonyolultabbak, összetettebbek, mintsem csupán a lehullott csapadék alapján az altalaj víztartalma, teherbírása megbízhatóan becsülhető lenne.
A leírt módszerrel az altalaj méréskori teherbírása számítható, így az évszaki szorzó az eddigi módszereknél lényegesen megbízhatóbban határozható meg.
Billenőkaros behajlásmérés bizonytalanságai
A hatályos méretezési utasításunk a billenőkaros behajlásmérésen alapul, de a mérés a korszerű és pontos dinamikus mérésekhez képest rendkívül bizonytalan, megbízhatatlan, ezért időszerű lenne ennek a mérési módnak elhagyása a méretezési módszerünkből.
A billenőkaros teherbírásmérést statikus mérésnek hívjuk, de ez egyáltalán nincs így. A „statikus” és dinamikus mérések közötti eltérést a mérés természetén, körülményén kívül – amit már előzőleg tisztáztunk és pontosítottunk – döntően a terhelési idő különbsége okozza.
Dinamikus méréseknél a felterhelési idő, jelen esetben 25 ms viszonylag pontos érték, evvel szemben a billenőkaros behajlásmérésnél a mérést végző személyzettől függ a mérés időtartama.
Nem elhanyagolható, hogy a terhelő gépjármű leállított motorral vagy járó motorral terhel. Általában utóbbi a mérési körülmény, e miatt a teljes pályaszerkezet „rezeg”.
Szintén nem elhanyagolható, hogy a terhelő jármű mióta terheli a mérőhelyet, és a tehermentesítés után mikor olvassuk le a mérőórákat.
Az is befolyásolja a mérés eredményét, hogy a szembejövő sávon mekkora a teherforgalom, ez utóbbi nem csak azért fontos, mert dinamikus többletterhelést okoz, hanem azért is, mert feszültségmentesíti a pályaszerkezetet a mérő oldalon, ennek következtében megnöveli a mért behajlást.
Minden típusú mérésnél a felterhelési idő függvényében a tehermentesítés után a teljes pályaszerkezetben és magában a földműben is visszamarad feszültség. A jelenség nem anyagállandó, abban az értelemben, mint a rugalmassági modulus, de függ tőle.
A jelenség eltér minden ismert anyagmodelltől, mert nem fejezhető ki az idő folytonos függvényeként.
A legjobban úgy tudjuk szemléltetni, mint a hüvelybe helyezett acél rugót, amely szorosan érintkezik a hüvely oldalával, ami érdes és finom homokkal szennyezett. Ha a rugót terheljük összenyomódik, a tehermentesítés után azonban a szennyeződés miatt „akadni” fog, nem nyeri vissza azonnal az eredeti alakját. Ha a hüvely falát rezgetjük, akkor a rugó idővel az eredeti alakját visszanyeri, vagyis feszültségmentessé válik a rugó. A feszültségmentesülés folyamata nem jellemezhető, modellezhető az idő folytonos függvénnyel.
Statikus mérésnél, főleg új pályaszerkezetek esetén a tömörödés valós jelenség, de a forgalom hatásának kitett pályaszerkezetek esetén már nem valószínű, dinamikus méréseknél pedig kizárható, hogy a teherbírásmérés közbeni tömörödés a mérhető tartományba esne.
Billenőkaros behajlásmérés esetén a pályaszerkezetben jelentős feszültség marad vissza, ebből következően a rugalmas visszaalakulás alapján mért behajlást a maradó feszültség befolyásolja. 1985. évben saját méréseink [3] alapján vizsgáltuk a feszültségmentesítés hiánya miatt a mért behajlásban elkövetett hibát, amely a pályaszerkezet függvényében 0,1-0,5 mm körül volt.
A billenőkaros behajlásmérésen kívül nincs más olyan helyszíni teherbírásmérés, ahol rugalmas visszaalakulást mérnénk. A gördülőkerekes mérések és az FWD mérések esetén mindig a teljes behajlást mérjük, vagyis nem számít, hogy mekkora a maradó feszültségből származó – a mérési időn kívüli – rugalmas visszaalakulás mértéke. Az FWD méréseknél, ahol a mérőkészülék tömege elhanyagolható, evvel nem kell számolni. A gördülőkerekes méréseknél az első kerekek terhelése már nem elhanyagolható. Az első kerék terheléséből visszamarad feszültség, ami hat a hátsó kerekek által okozott teljes behajlásra, annak értékét csökkenti a maradó feszültségtől függően. Ezt a hatást szemléltettem a 7. ábrán, ahol az eredeti Curviométeres mérés és az elméleti feszültségmentesítés utáni behajlási teknőt ábrázoltam. A következmény a behajlási teknő párhuzamos eltolódása.
 |
FDW mérésnél is előfordulhat, hogy nagy nehézforgalom esetén ráterhelnek a mérőpontra, amely ponton a pályaszerkezet a mérés megkezdésekor még nem tehermentesült. A nehéz teherforgalom sebessége viszont elég magas, így a hatás is kicsi (8. ábra).
FDW méréseknél legalább két mérésre van szükség, ezért az első mérés miatt a pályaszerkezetben már lesz maradó feszültség, ennek következtében terhelésenként a mért behajlás ~1%-al csökken, három felterhelés esetén ~2%, ami minden mérőpontra kivétel nélkül igaz. A behajlási teknő eltolódása nem párhuzamos, hanem mérőpontonként %-os érték, hasonlóan a billenőkaros behajlásméréshez, ahol a pályaszerkezetben maradó feszültség egy horizontálisan nem mozgó pontból származik.
Curviométeres méréskor a pályaszerkezetben maradó feszültség miatt egy állandó hiba keletkezik, amit a mért behajlási teknők alakja szerinti rugalmassági modulusok visszaszámításnál minden esetben észlelünk, ha ábrázoljuk a visszaszámítás eredményeit számítás közben.
A visszaszámításnál jelentkező hiba állandó, ezért viszonylag egyszerűen korrigálható eltolással.
Billenőkaros behajlásmérésnél a maradó feszültségből származó összenyomódás nem elhanyagolható és nem korrigálható, mivel nem mérünk behajlási teknőt. A 7. ábrán egy szélsőséges esetet tüntettem fel, ahol a dinamikus teherbírásmérésből számított (Billenőkaros UME szerint) kapott behajlást hasonlítottam egy elméletileg „tökéletesen” feszültségmentesített behajlási teknőben mért billenőkaros behajláshoz.
A billenőkaros mérésre hatással van a mérőórák leolvasásának gyorsasága, valamint a leolvasás idejében elhaladt nehéz teherforgalom mértéke, amely hatékony feszültségmentesítést eredményez
A különböző terhelési idejű készülékek mérési tapasztalata alapján a következő becslést adom a mérést követően a pályaszerkezetben maradó összenyomódás, behajlás és a terhelés sebessége közötti összefüggés jelleggörbéjére (8. ábra).
 |
Végül rátérhetünk az 1998. évi (1) és a 2006. évi (5) átszámítások lehetséges okainak magyarázatára, ahol feltételezzük, hogy mindkét esetben a kutatók, akik a méréseket végezték lelkiismeretes munkát végeztek, vagyis mindkét esetben a mérések jók voltak. Az eltérés az MSZ szerinti mérés ismételhetőségének alacsony megbízhatóságával magyarázható.
Lehetséges fő eltérések a két vizsgálat során, amit a mérési szabvány [1] nem szabályoz:
- az ikerkerekek abroncsainak mérete és abroncsnyomása
- a terhelési idő, a mérési időtartama
- a tehermentesítés után a leolvasási idő
- a nehézjármű forgalom a leolvasási idő alatt
- a pályaszerkezet felépítése, vastagsága
Évszaki szorzó számítása közvetlenül a dinamikus mérésekből
Az évszaki szorzók meghatározása a (6) szerint a dinamikus mérésekből statikusra átszámított rugalmassági modulusokkal történt. Az évszaki szorzók azonban közvetlenül a dinamikus mérésekből is számíthatók.
A homogén útszakaszon a dinamikus mérésből a körtárcsa tengelyében mérve kapjuk a behajláshoz tartozó \( S_{din} \) behajlást (9. ábra).
Az útszakaszra jellemző altalaj talajcsoportjának ismeretében az e-UT 06.03.13:2005 5.1 táblázata alapján felvett \( E_{2talaj} \) talaj teherbírási modulust az 1,71 „k” értékkel felszorozzuk, így megkapjuk a mértékadó \( E_{2talajdin} \) talajteherbírást, amellyel számítjuk a dinamikus tárcsás mérés legnagyobb behajlás mértékadó értékét. A két behajlás értékének hányadosa (9. ábra) adja a dinamikus évszaki szorzót. A dinamikus és a statikus évszaki szorzó közel azonos, de a billenőkaros behajlás alapján meghatározott évszaki szorzó a mérés sajátságai miatt ettől eltér, kevesebb.
\[ c_{édin}=\frac{S_{mdin}}{S_{din}} \]
A 3. táblázatban szereplő szakaszon az \( S_{din}=0,342\ mm, S_{mdin}=0,716\ mm, cédin=2,09 \)
 |
Behajlási teknő mérésére alkalmas készülék a gördülőkerekes Curviométer is, amely készüléket szintén használjuk hazánkban. A Curviométer által előállított behajlási teknőkből is vissza lehet számolni a pályaszerkezeti rétegek rugalmassági modulusát, ezért az évszaki szorzók is számíthatók.
A Curviométer és a dinamikus ejtősúlyos készülékek eltérő terhelési idővel rendelkeznek, ezért szükséges a készülékek közötti átszámítás módszer elméleti és összemérés alapján megalapozott igazolása.
Azt már tudjuk, hogy a 8-72 km/h sebességű terhelő tehergépkocsik 0-35 oC hőmérsékleti tartományon belül a vizsgálatban szereplő pályaszerkezetekre vonatkozóan a rugalmassági modulusokat közel azonos mértékben, arányban változtatják [7].
A BME Építőanyagok Tanszékén dr. Zsigovits Istvánnal az INSTRON készülékén 0,02; 0,05; 0,1; 0,2; 0,5; 1,0 mm/perc terhelési sebesség mellett vizsgáltunk aszfalt keverék mintákat 25 oC-on.
A mérési eredmények feldolgozása után a kapott összefüggések:
exponenciális
\[ E_r=c{\ f}^{0,15} \]
logaritmikus
\[ E_r=a-bln(T) \]
ahol:
\( E_r \)- rugalmassági modulus (MPa)
\( f \)- mérési frekvencia (Hz)
\( T \)- felterhelési idő (sec)
\( a,b,c \)- constansok (MPa)
A 0,1 – 10 Hz tartományon belül a (8), vagy (9)-nek teljesülnie kell minden egyéb mérésre, így a helyszíni teherbírásmérésekre is, azt azonban figyelembe kell venni, hogy az összefüggést a hőmérséklet is befolyásolja [8].
A következő mérési módokra határoztam meg a mérési frekvenciákat
| Mérés típusa | Sebesség (km/h) | Terhelési idő (sec) | Frekvencia (Hz) |
| Billenőkaros | – | ~60 | ~0,008 |
| Lacroix | 3 | 4,8 | 0,104 |
| Curviometer | 18 | 0,8 | 0,625 |
| Dynatest&KUAB | – | 0,025 | 20,00 |
Billenőkaros terhelés esetén a ~60 s becslés, míg a Lacroix és a Curviométer esetén 4 méter távolság megtételéhez szükséges időből számoltam. A Dynatest és a Magyar Közút által használt KUAB esetén az alkalmazott frekvencia mérési paraméter.
A 2021. évi összemérés során a Curviométer és a Dynatest méréssel a kapott arány „k” tényező 1,65; míg az exponenciális (8) összefüggéssel kapott érték 1,68.
| Típus | Curviometer | FDW&KUAB |
| Lacroix* | 0,76 | 0,45 |
| Curviometer | 1,00 | 0,60 |
| FWD&KUAB | 1,68 | 1,00 |
*: nincs összemérés
A dinamikus tárcsás mérésekből nemcsak az (5) szerint számított behajlást tudjuk összehasonlítani a mérésekből számított billenőkaros behajlással (5. ábra), hanem összehasonlíthatjuk a dinamikus teherbírásmérés mért értékével is. Így megkapjuk az (5) UME előírást jól közelítő, elméletileg megalapozottabb – a konstans tagot nem tartalmazó -(10) összefüggést (10. ábra).
 |
\[ S_{stat}=1,105\ S_{din} \]
A mért billenőkaros behajlás és a dinamikus behajlások közötti arány (10) 1,105.
A Curviometer és a Dynatest méréseknél a dinamikus rugalmassági modulusok aránya 1,65, míg a Dynatest és a billenőkaros behajlás rugalmassági modulusok aránya 1,71, ezért a Curviométer és a billenőkaros mérés rugalmassági modulusainak aránya 1,71/1,65 = 1,04.
A kétrétegű rendszerre egyszerűsített modellek alkalmazása esetén az évszaki szorzó számításánál az e-UT 06.03.13:2005 5.1 táblázata alapján felvett \( E_{2talaj} \) talaj teherbírási modulust az 1,04 értékkel kell felszorozni, ha a Curviométer behajlási teknőjéből kívánjuk az évszaki szorzót meghatározni.
\[ E_{2talajcurv}=1,04\ E_{2talaj}\ \]
Évszaki szorzók számításának menete többrétegű és kétrétegű rendszerben
Pontos számítási modelleknek azokat tekinthetjük, amelyek segítségével a mért behajlási teknőből a pályaszerkezeti rétegek rugalmassági modulusa visszaszámítható. A módszerek hátránya, hogy minden estben valamilyen a kereskedelmi forgalomban hozzáférhető program használatához van kötve, amelyek közvetlenül nem csatolhatók a mérési eredmények feldolgozási programjaihoz, vagyis használatuk nehézkes, bonyolult és nagyon időigényes.
Az évszaki szorzók számítására, ezért megadok egy egyszerűsített kétrétegű rendszeren alapuló közelítő módszert is.
Bármilyen módszer, programok használata esetén első lépésben a mérési eredményekből először homogén szakaszokat képzünk, ahol törekedni kell arra, hogy legalább 30 mérési pont álljon rendelkezésre. Homogén szakaszképző a forgalom, a pályaszerkezet felépítése, a mért legnagyobb behajlás, a mérési hőmérséklet és az útszakasz állapota.
A mérési hőmérsékletet általában nem szoktuk homogén szakaszképzőnek tekinteni, mivel a (4) szerint korrigálhatjuk a legnagyobb behajlás értékét. A mérési tapasztalat szerint sok esetben – főleg napsütéses időszakban – a mért burkolat-hőmérséklettel korrigálatlan, „nyers” adatok szórása lényegesen kisebb, mint a hőmérséklettel korrigált adatoké, ami azt jelenti, hogy a korrekció nem megfelelő, nem éri el célját.
Következő lépés a homogén szakaszonként a behajlási teknő minden pontjára – 0; 200; 300; 450; 600; 900; 1200; 1500; 1800 – a mértékadó behajlások számítása.
Az így nyert behajlási teknőből számítjuk vissza pályaszerkezeti rétegenként és az altalajra vonatkozó rugalmassági modulusokat.
A pályaszerkezeti rétegek vastagságát és típusát fúrt mintákból és az OKA adatbázisból együttesen határozzuk meg. OKA adatbázisból kapjuk a homogén szakaszra vonatkozó talajcsoportot is, de a talajmechanikai vizsgálaton alapuló talajcsoport meghatározása lényegesen pontosabb, megbízhatóbb adatokat szolgáltat.
Az egyes pályaszerkezeti rétegek együttdolgozására vonatkozóan a visszaszámítás során teszünk előfeltételezést, amelynek helyességét, vagy helytelenségét a számított és mért behajlási teknő közötti eltérés igazolja vagy cáfolja.
A visszaszámítás során kapott behajlási teknő legnagyobb behajlási értéke az \( S_{din} \).
Adott mérési módhoz meghatározzuk a mértékadó dinamikus talajteherbírást:
Curviométer esetén: \( E_{2talajcurv}=1,04\ E_{2talaj} \)
Dynatest és a Magyar Közút KUAB készüléke esetén: \( E_{2talajdin}=1,71\ E_{2talaj} \)
A visszaszámításból kapott pályaszerkezeti rétegek rugalmassági modulusaival és a mértékadó \( E_{2talajcurv} \) vagy \( E_{2talajdin} \) a mérési módtól függő dinamikus talajteherbírással kiszámoljuk a legnagyobb behajlás értékét \( S_{mdin} \). Az évszaki szorzó, így a (7) szerint már számítható.
A 3. táblázatban szereplő rétegrenddel Dynatest méréssel az évszaki szorzó \( c_{édin}= 1,98 \) a BISAR program alapján, saját Rodcont programunkkal 2,05.
A visszaszámító programok hozzáférésének korlátozott volta és bonyolult kezelhetőség miatt az évszaki szorzó számítását egyszerűsített kétrétegű rendszerre is megadom.
A kétrétegű rendszert úgy értelmezzük, hogy a pályaszerkezeti rétegeket az útalappal együtt pl. rakott alap összevonjuk egy réteggé, amely alatt már csak az altalaj van.
Méréskor ill. a mérési eredmények feldolgozásakor az OKA adatbázisból, vagy helyszíni vizsgálatokból kapjuk a teljes pályaszerkezet vastagságát és a talajcsoportot.
A 3. táblázat adatait figyelembe véve a rétegvastagság 495 mm az \( E_{2talaj}= 30 MPa \),
Dynatest mérést feltételezve, \( E_{2talajdin}=1,71\ E_{2talaj}=51\ MPa \).
Ismeretlen viszont a méréskori \(E_a \) talajteherbírás és az \( E_f a h=495 mm \) vastagságú összevont pályaszerkezet rugalmassági modulusa.
Mielőtt rátérnék az egyszerűsített számítás ismertetésére a BISAR program segítségével bemutatom a többrétegű és a kétrétegűre összevont rendszer közötti lényeges eltérést a 3. táblázat adatai alapján. Mind a kétrétegű, mind a többrétegű rendszerre a számításokat a BISAR programmal végeztem.
A többrétegű rendszer az eredeti rétegrendnek megfelelő, míg a kétrétegűnél a rétegvastagságot szorozni kell az Odemark-féle korrekciós tényezővel [10] „n”, így a rétegvastagság = nh.
Az összevont rétegek \( E_f \) rugalmassági modulusát (13)-ből számítjuk.
Az 1. táblázat szerinti pályaszerkezet eredeti behajlási teknőjét közelítő 1150 MPa rugalmassági modulussal számoltunk (11. ábra), ahol a talaj rugalmassági modulusa 174 MPa.
 |
A kétrétegűvé alakított rendszerek kizárólag a 0; 1200; 1500; 1800 pontokra illeszthetők, mert a 0 – 900 közötti szakaszon már alapvetően eltérnek a mért értékektől, amely pontokon mért behajlások már csak a többrétegű rendszereket is kezelni tudó programokkal közelíthetők.
Kétrétegű rendszerben a legjobb közelítést az n=0,72 korrekciós tényező mellett kaptam, szemben a hatályos előírásban szereplő n=0,9 –el. A számított évszaki szorzó n=0,9 esetén \( c_{édin}= 1,83 \), míg n=0,72 esetén \( c_{édin}= 1,92 \).
A többrétegű rendszer alkalmazásával kapott évszaki szorzóhoz \( c_{édin}=1,98 \).
Az eltérés oka, hogy a több réteget is összevonó kétrétegű rendszer a valóságban nem helyettesíti a többrétegű rendszert, a hiba annál nagyobb minél több eltérő rugalmassági modulusú rétegeket vonunk össze, a hibát növeli, ha a rétegek nem dolgoznak együtt.
A hazai méretezési módszerünk Odemark-féle [9] kétrétegű rendszeren alapul, ezért az évszaki szorzó számításának egyszerűsített módszerét ezek alapján fogom bemutatni, amely a BISAR programhoz viszonyított egyszerűsítések miatt további pontatlanságot tartalmaz. Az egyszerűsített kétrétegű rendszer alkalmazása, amely a helyettesítő rétegvastagságon alapuló MET módszer alkalmazása, éppen egyszerűsége és viszonylagos pontossága miatt a mai napig ajánlott [12].
Kétrétegű rendszerben a terhelő rugalmas tárcsa tengelyében számított, rétegenkénti összenyomódásokat a UME előírásban [2] is használt, az 1993-as AASHTO tervezési útmutatóban is megtalálható [11], számítást alkalmazzuk:
\[ S_0^{0-\infty}=2\left(1-\mu^2\right)pr\left(\frac{1}{E_a\sqrt{\left[1+n^2\left(\frac{E_f}{E_a}\right)^{2/3}\left(\frac{h}{r}\right)^2\right]}}+\frac{1-\frac{1}{\sqrt{\left[1+\left(\frac{nh}{r}\right)^2\right]}}}{E_f}\right) \]
\[ E_f=E_a\left(\ \frac{z}{nh}\right)^3 ; z=nh\ \left(\frac{E_f}{E_a}\right)^{1/3} \]
\[ z^2={n^2h}^2\ \left(\frac{E_f}{E_a}\right)^{2/3};\ \left(\frac{z}{h}\right)^2=n^2\left(\frac{E_f}{E_a}\right)^{2/3} \]
\[ S_0^{0-\infty}=\frac{1,5pr}{E_a}\left(\frac{1}{\sqrt{\left[1+\left(\frac{z}{r}\right)^2\right]}}+\frac{1-\frac{1}{\sqrt{\left[1+\left(\frac{nh}{r}\right)^2\right]}}}{\left(\frac{z}{nh}\right)^3}\right) \]
ahol:
n – Odemark-féle korrekciós tényező
h – altalaj feletti pályaszerkezeti réteg vastagsága (mm)
z – helyettesítő rétegvastagság (mm)
r – a terhelő rugalmas körtárcsa sugara (mm)
\( \mu \) – Poisson szám, UME szerint = 0,5
p – terhelő tárcsa alatti nyomás (MPa)
\( E_f \) – altalaj feletti pályaszerkezeti réteg rugalmassági modulusa MPa
\( E_a \) – az altalaj rugalmassági modulusa MPa
\( S_0^{0-\infty} \)- a tárcsa tengelyében számított legnagyobb behajlás (mm)
Kétrétegű rendszerben számíthatjuk a terhelő tárcsától x távolságban lévő mérőpontokon a rétegenkénti összenyomódásokat [10], ha x>>r.
A helyettesítő rétegvastagság alatt a teljes összenyomódás a terhelő tárcsától x távolságban:
\[ S_x^{z-\infty}=\frac{P}{2x\pi E_a}3xR-13 xR3-μxR3+1-2µxR+2z-Rx \]
\( R=\sqrt[2]{(z^2+x^2)} \)
E_a rugalmassági modulusú homogén és izotrop féltérben a teljes összenyomódás a terhelő tárcsától x távolságban:
\[ S_x^{0-\infty}=\frac{P}{x\pi E_a}\left(1-\mu^2\right) \]
AASHTO tervezési útmutató [11], [12] szerint:
\[ E_a=\frac{0,24P}{xS_x} \]
\( S_x \) – a tengelytől „x” távolságra mért behajlás (mm)
A h vastagságú pályaszerkezet összevont rugalmassági modulusa \( E_f \), ezért a 0-z mélység között az összenyomódás:
\[ S_x^{0-z}=\ \left(S_x^{0-\infty}-S_x^{z-\infty}\ \right)\frac{E_a}{E_f} \]
\( \mu=0,5 \) esetén
\[ S_x^{z-\infty}=\frac{P}{2x\pi E_a}\left|\frac{3x}{R}-\ 1,5\left(\frac{x}{R}\right)^3\right|=\frac{0,75P}{x\pi E_a}\left|\frac{2x}{R}-\left(\frac{x}{R}\right)^3\right| \]
\[ S_x^{0-z}=\frac{0,75P}{x\pi E_f}\ \left(1-\left|\frac{2x}{R}-\left(\frac{x}{R}\right)^3\right|\ \right) \]
\[ S_x^{0-\infty}=\frac{0,75P}{x\pi E_a}\left[\frac{1-\left|\frac{2x}{R}-\left(\frac{x}{R}\right)^3\right|}{\left(\ \frac{z}{nh}\right)^3}+\left|\frac{2x}{R}-\left(\frac{x}{R}\right)^3\right|\right] \]
ahol:
\( S_x^{z-\infty} \) – a tárcsa tengelyétől x távolságnál számított összenyomódás (mm) \( z-\infty \) között,
\( S_x^{0-\infty} \) – a tárcsa tengelyétől x távolságnál számított összenyomódás (mm) \( 0-\infty \) között,
teljes behajlás.
\( S_x^{0-z} \) – a tárcsa tengelyétől x távolságnál számított összenyomódás (mm) \( 0-z \) mélység között.
A számításokat fokozatos közelítéssel tudjuk elvégezni. Első közelítésként felvesszük a (18) AASHTO ajánlás szerinti \( E_a \) számított értékek átlagát. Az átlagot az x=900; 1200; 1500; és 1800 mm-re lévő pontokból számítjuk. A felső réteg \( E_f \) kezdeti rugalmassági modulusának az \( E_f=1000\ MPa \) vesszük fel.
A kezdeti értékek felvételét követően számoljuk a (13) alapján „z” kezdeti értékét, a (15) és a (22) alapján számítjuk a teljes behajlásokat a 0; 900; 1200; 1500; 1800 mérőpontokra.
Az 1200; 1500; 1800 pontokra a mért és számított behajlásokra (23) szerint számítjuk az eltérési hibát, ahol törekedni kell a számított RMS% hiba minimálizálására.

ahol:
∆ – a mérőeszköz mérési hibája, KUAB, Dynatest esetén \( \pm0,002 mm \)
k – mért pontok száma: 3 db, 1200, 1500 és 1800 távolságok esetén
Az RMS% hibát az \( E_a \) talajteherbírás kezdeti értékének változtatásával tudjuk csökkenteni, mindig lesz egy olyan \( E_a \) érték, ahol a „z” helyettesítő rétegvastagság mellett, az RMS% hiba minimális.
Ha az RMS% elérte minimumát, akkor változtatjuk a helyettesítő rétegvastagság „z” értékét, hogy az összes vizsgált pontra 0; 900; 1200; 1500; 1800 számolva az RMS% minimális legyen. A „z” értékének változtatása hat a (23)-ra, ezért az \( E_a \) értékét ismét változtatjuk, amíg a hiba megfelelő nem lesz, ezt követően „z” értékét ismét változtatjuk. A ciklust addig folytatjuk, amíg az RMS% eléri minimumát.
A számítási eredményeket számítás közben érdemes ábrázolni is (12. ábra).
 |
Az egyszerűsített kétrétegű módszerrel a 3. táblázatban szereplő paraméterekkel BISAR programmal számított behajlási teknő alapján a n=0,8\ korrekciós tényezővel a kapott \( E_a=164\ MPa,\ \) míg az Ef=925 MPa;h=495 mm és \( S_{din}=0,31\ mm \).
Ha a méréskori \( E_a \) helyett \( E_{2talaj}=51\ MPa \) számolunk, akkor a (11) szerint számított mértékadó legnagyobb behajlás \( S_{mdin}=\ 0,555\ mm \), és \( c_{édin}=1,77 \).
Jelen példánál az egyszerűsített módszer szerint számított \( c_{édin}=1,77 \), eltér a pontos többrétegű rendszerrel számított 1,98-tól, amelynek fő oka, hogy az egyszerűsített módszer csak együttdolgozó rétegeket tud figyelembe venni. Ha a BISAR programmal is együttdolgozó rétegekkel számolnánk, akkor az évszaki szorzó 1,83-ra adódna, amely már alig tér el a közelítő módszerrel számított 1,77-től.
Megvizsgáltuk mekkora hibát okoz, ha az útalap vastagságában 100 mm-t tévedünk, ha a rakott alap 150 mm helyett 250 mm.
\( E_a=162\ MPa, \) míg az \( Ef=843 MPa \) ;h=595 mm és \( S_{din}=0,313\ mm \)
Ha a méréskori \( E_a \) helyett \( E_{2talaj}=51\ MPa \) számolunk, akkor a (12) szerint számított mértékadó legnagyobb behajlás \( S_{mdin}=\ 0,514\ mm \), és \( c_{édin}=1,67 \).
Az évszaki szorzó számításánál elkövetett hiba 6%.
Az n=0,8 korrekciós tényező alkalmazását tartjuk indokoltnak, ha az útalap félig merev, vagy hajlékony pl. rakott alap, szórt alap, mechanikai stabilizáció stb. és az esetleges higított bitumenes rétegen felül a meleg aszfaltkeverék legalább 12 cm.
A számított értékek jól közelítik a többrétegű rendszerben számított pontos számítási módszerek által kapott eredményt, a pontosság \pm10%.
A leírt közelítő módszer a többrétegű rendszereket modellezni képes programokhoz képest viszonylag pontatlan, de sokkal megbízhatóbb, mint a jelenleg alkalmazott évszaki szorzók [2], amelyek a valóságban konkrét útszakaszon 1,0 – 2,4 között bármilyen értékűek lehetnek (lásd. 1. 2. táblázatokat).
Összefoglalás
A mértékadó teherbírás számításához használt, jelentős pontatlanságot okozó e-UT 06.03.13:2005 UME szerinti évszaki szorzók kiváltására kétféle módszert mutattam be.
Az egyik módszer a mért behajlási teknők alapján a rendelkezésre álló méretező programok segítségével lehetővé teszi az évszaki szorzó számítását.
A másik egy egyszerűsített eljárás – amely az Odemark-féle módszeren alapul, amelynek segítségével kevésbé pontosan, de a jelenlegi gyakorlathoz képes jelentősen pontosabban lehetséges az évszaki szorzó meghatározása.
Igazoltam, hogy az ejtősúlyos FWD mérésből kapott behajlási teknő átszámítható „statikus” mérések alapján kapott behajlási teknővé a pályaszerkezeti rétegek rugalmassági modulusainak konstans értékkel történő szorzásával, ami szükséges a különböző teherbírási mérési módszerek közötti átszámításhoz.
Elemeztem a billenőkaros behajlásmérésben rejlő hibák okait, amely hibák és pontatlanságok nem küszöbölhető ki, a hibák nagyságrenddel nagyobbak, mint a gördülőkerekes vagy az ejtősúlyos FWD mérések esetén.
Irodalomjegyzék
[1]: MSZ 2509/4-1989 „Útpályaszerkezetek teherbíró képességének vizsgálata”.
[2]: e-UT 06.03.13:2005 „Aszfaltburkolatú útpályaszerkezetek méretezése és megerősítése”, 7.1. táblázat.
[3]: Zsichla, L. 1988: A pályaszerkezet gazdaságos megerősítése annak egyenérték rugalmassági modulusa alapján számított behajlás segítségével, KTI.
[4]: Love, A.E.H. 1906: Treatise on the Mathematical Theory of Elasticity. University Press, Cambridge, p. 260.
[5]: Burmister, D. M. 1945: The General Theory of Stresses and Displacements in Layered Systems. I. Journ. Appl. Physics, vol. 16.
[6]: Király, T., Primusz, P. 2020: A gumiabroncs és az útpályaszerkezet érintkezési kapcsolatának elemzése végeselem módszerrel, Útügyi lapok, 8. évfolyam, 14. szám. https://doi.org/10.36246/UL.2020.2.04
[7]: Al-Qadi, IL, Loulizi, A, Elseifi, M & Lahouar, S. 2004: The Virginia smart road: The impact of pavement instrumentation on understanding pavement performance, Asphalt Paving Technology, AAPT, pp. 427-465.
[8]: Francken, L. Ed. 1998. Bituminousbinder and mixes. RILEM Report 17. London (UK): E&FN Spon. https://doi.org/10.1201/9781482271973
[9]: Odemark, N. 1949: Undersökning av elasticitetsegenskaperna hos olika jordarter samt teori för beräkning av beläggningar enligt elasticitetsteorin. Statens Väginstitut, Stockholm.
[10]: Zsichla, L. 2021: Számítási módszer a behajlási teknő megbízható modellezéséhez; Útügyi lapok, 9. évfolyam, 15. szám. https://doi.org/10.36246/UL.2021.1.06
[11]: American Association of State Highway and Transportation Officials. 1993: Guide for Design of Pavement Structures. American Association of State Highway and Transportation Officials, Washington, DC.
[12]: Smith, K. D., Bruinsma, J. E., Wade, M. J., Chatti, K., Vandenbossche, J. M. & Yu, H. T. 2017: Using Falling Weight Deflectometer Data with Mechanistic Empirical Design and Analysis, Volume I: Final Report, Federal Highway Administration, p. 64.
Erre a szövegre így hivatkozhat:
Zsichla László: Évszaki szorzók, talajteherbírási modulus számítása a mért behajlási teknők segítségével, billenőkaros behajlásmérés bizonytalansága, 2023, DOI: 10.36246/UL.2023.1.06
