https://doi.org/10.36246/UL.2024.2.07
2024; 12. évfolyam, 20. szám
Pdf: Az aszfaltkeverékek tulajdonságainak hőmérsékletfüggése a termodinamika törvényei alapján
Bevezetés
A közúti közlekedési pályák, pályaszerkezetek tervezésével vagy üzemeltetésével foglakozó mérnökök gyakran teszik fel a következő gyakorlati kérdést.
Ha megmértük – helyszínen vagy laboratóriumban – egy aszfaltkeverék komplex modulusát adott frekvencián és hőmérsékleten, akkor egy másik frekvencián és hőmérsékleten mekkora a várható komplex modulus értéke, a becslést milyen hibával tehetjük meg?
A kérdésre fontos lenne egzakt választ adni, hiszen az útpályaszerkezeten belül a hőmérséklet folyamatosan és jelentősen változik. A frekvencia se állandó, mivel az útpályaszerkezeten belül a frekvencia a mértékadó tehergépjárművek sebességétől függ, így jelentősen más átkelési szakaszon vagy, autóúton és autópályán. A sebesség különbözik a csomópont előtt és két csomópont között is.
A hőmérséklet és a frekvencia a komplex modulus értékét, akár 10-20 szorosára, hányadára változtathatja. A komplex modulus viszont befolyásolja az útpályaszerkezetben keletkező feszültségeket még teljesen azonos terhelés esetén is, így jelentősen hat a várható élettartamra. A tervező mérnökök tervezési, míg az üzemeltető mérnökök várható élettartamról beszélnek.
Amióta aszfalt útpályaszerkezet létezik, a nagyon gyakorlati kérdésre azóta sincs egzakt válasz.
Az aszfaltkeverékek komplex modulusának hőmérsékleti függésével számtalan tanulmány foglalkozott. Az eddig elért tudományos eredmények alapján javasolt egyenletek, összefüggések a feltett kérdésre nem vagy a gyakorlat számára nehezen hasznosítható választ adnak.
A tanulmány célja az aszfaltkeverékek komplex modulusának frekvencia-hőmérséklet összefüggésének – eltolási függvény – pontosítása, a termodinamika segítségével, ahol az elméletem független igazolására a következő jól publikált vizsgálati eredményeket használtam fel, [1, 2, 3, 4].
A feltárt összefüggések elemzések nem oldják meg az elmúlt évtizedek hiányosságait, de talán közelebb visznek a kérdésre adott pontosabb válaszok megadásában.
Mestergörbe eltolási függvénye
| Hőmérséklet (oC)/Komplex modulus (MPa) | ||||||
| (Hz) | -10 | 4,4 | 21,1 | 37,8 | 54,4 | |
| 25 | 25440 | 16581 | 8575 | 4238 | 1504 | |
| 10 | 24150 | 14813 | 7321 | 3498 | 1200 | |
| 5 | 22781 | 13710 | 6302 | 2792 | 985 | |
| 1 | 20048 | 11191 | 4503 | 1752 | 655 | |
| 0,5 | 18791 | 10168 | 3898 | 1481 | 578 | |
| 0,1 | 15703 | 7951 | 2722 | 1044 | 450 | |
Az eltolási függvény segítségével a különböző hőmérsékleten mért komplex modulusokat a frekvencia mentén úgy toljuk el, hogy azok egyetlen referencia hőmérsékletre vonatkozzanak. A „legjobb” eltolási függvény az, amelyik az egy referencia hőmérsékletre vonatkozó komplex modulusokra illesztett un. Sigmoid függvény a legkisebb RMS%-ot adja eredményül.
A Sigmoid függvény a referencia hőmérsékleten – az 1. ábrán 21.1 oC –on – megadja, a mérési frekvencia komplex modulus összefüggését.
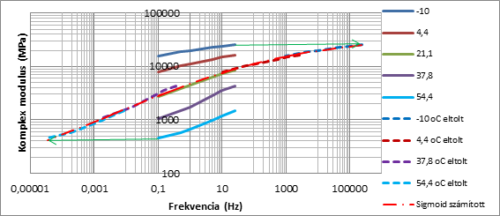 |
Az eltolási függvény (1) megadja azt a \( f_{sz} \) eltolási frekvenciát, amely a \( T_{b} \) hőmérsékleten és \( f_{b} \) frekvencián mért komplex modulus értékét változatlanul hagyja egy tetszőlegesen választott \( T_{r} \) referencia hőmérsékleten. A \( T_{r} \) hőmérsékleten és frekvencián mért komplex modulusnak egy megadott hibahatáron belül meg kell egyeznie a \( T_{b} \) hőmérsékleten és \( f_{b} \) frekvencián mért komplex modulus értékével.
Az eltolási függvény a terhelési frekvencia és a vizsgált test hőmérséklete között biztosít kapcsolatot (1), aminek termo dinamikai háttere van.
\[ f_{sz}=a_T f_b \]
ahol:
\( a_T \) – eltolási függvény
\( f_sz \) – számított eltolási frekvencia (Hz)
\( f_b \) – bázis vagy mérési frekvencia (Hz)
\( T \) – hőmérséklet (K)
Termodinamikai megfontolásokkal nemcsak az eltolási függvény, hanem a (2) Sigmoid frekvencia-komplex modulus összefüggés is feltárható, ami majd egy új összefüggéshez vezet. A továbbiakban a komplex modulusra az EK jelölést fogom alkalmazni, mivel a termodinamikában az \( E_a \) jelölés és indexelés az energiára vonatkozik és jelen tanulmány alapvetően a termodinamikára alapoz.
\[ EK=e^{\left[a+\frac{b}{1+e^{-\left[c+d\ f_{sz}\right]}}\right]} \]
ahol:
\( EK \) – számított komplex modulus (MPa)
\( a;b \) – számított eltolási paraméterek (MPa)
\( c;d \) – számított dimenzió nélküli paraméterek
\( T_r \) – referencia hőmérséklet, amely hőmérséklethez viszonyítunk (K)
\( T_b \) – bázis vagy mérési hőmérséklet (K)
A Sigmoid (2) egyenlethez legalább négy illesztési paraméter szükséges. Az paraméter a komplex modulus tengelyén nagyít, míg a paraméter a frekvencia tengelyén nagyít. A paraméterek forgatást tesznek lehetővé. Sok szerző keres, keresett összefüggést az illesztési paraméterek és az aszfaltkeverék tulajdonságai között, bitumentartalom, hézagtérfogat, bitumen viszkozitása stb., de ezek az összefüggések természetüknél fogva empirikusak, ill. statisztikusak, így nem valós összefüggésen alapulnak. A statisztikus módszerek alkalmazásában kiemelkedik [5].
Ha valós ok-okozati összefüggéseket keresünk, akkor nem kerülhető el az (1) és a (2) egyenletek közvetlen termodinamikai levezetése.
Mielőtt rátérnék a termodinamikai tárgyalási módra röviden ismertetem a leginkább elterjedt három eltolási függvényt. A legszélesebb körben az un. WLF [6] módszert alkalmazzák:
\[ \log{a_T=\ -\frac{C_1\left(T_b-T_r\right)}{C_2+\left|T_b-T_r\right|}} \]
ahol:
\( C_1 \) ;\( C_2 \) – WLF függvény eltolási paraméterei
A (3) egyenlet közvetetten tartalmaz termodinamikai megfontolásokat, és viszonylag jól alkalmazható az aszfaltkeverékek eltolási függvényeként, de pontossága vitatható. A WLF módszerről általános kritikát fogalmaz meg [7]. A WLF (3) pontatlansága miatt [8], javasolják [9] módosított WLF egyenletének alkalmazását:
\[ \log{a_T=\ -\frac{C_1\left(T_b-T_k\right)}{C_2+\left|T_b-T_k\right|}}-\frac{\left(T_r-T_k\right)}{C_2+\left|T_r-T_k\right|} \]
A \( T_k \) az inflexiós ponthoz tartozó hőmérséklet, aminek azonban nincs termodinamikai alapja, a \( T_k \) hőmérséklet rögzítése önkényes, de célszerű.
Szintén elterjedten alkalmazzák a [10] polinomot eltolási függvénynek, amely nem felel meg a termodinamika törvényszerűségének, ennek ellenére a polinomok „kedvező” tulajdonsága, hogy a mérésekkel már feltárt tartományban és feltételek mellett jó közelítést biztosít.
\[ \log{a_T=\ a{T_r}^2+bT_r+c} \]
A Witczak-féle (5) eltolási függvénynek közvetlenül nincs köze a termodinamikához, ha viszont a kizárólag termodinamikai levezetésen alapuló összefüggések (6) vagy (36) eltolási függvények alkalmazásával kapott frekvencia-hőmérséklet eredményére a (5) jól illeszthető, vagyis a (5) egy jó, statisztikus módszer, bár sok esetben a megfelelő illesztés már harmadfokú.
Az eltolási faktorokat elemezték [11], megállapították, hogy a mért és az eltolási egyenletekkel kapott értékek különösen a magas és az alacsony hőmérsékleten tértek el egymástól. A tanulmány arra is rámutat, hogy az alkalmazott eltolási egyenletek alapvetően empirikus megközelítésen alapulnak.
Nem említettem az [12] szerint képzett lineáris eltolási modellt, amely a termodinamikán alapul, de erről a modellről a továbbiakban részletesen lesz szó.
Előzetesen itt ismertetem a kizárólag termodinamikai levezetésen alapuló „egyszerűsített” nem lineáris eltolási függvényt (6), ahol figyelembe vettem, hogy az \( E_a \) aktiválási energia a hőmérséklet függvényében változik.
\[ f_1=f_2\sqrt{{\ e}^{-\left[\frac{g\left(T_2-T_1\right)^2+h\left(T_2-T_1\right)}{\ T_2T_1}\right]}} \]
ahol:
\( g \) ;\( h \) – számított eltolási paraméterek (K)
A (6) összefüggés nagy előnye, hogy a négyzetes összefüggés miatt a hőmérséklet-frekvencia összefüggés közelítő módszerek nélkül is számítható.
A téma további tárgyalása termodinamikai ismertek nélkül már nem lehetséges, ezért a témakört a továbbiakban egy kicsit részletesebben fogom ismertetni. A termodinamika tárgyalási módszerében felhasználtam [13] és [14] által írt könyveket.
Termodinamikai elméleti háttér
Egy anyag tulajdonságainak, így a viszkozitásának vagy a komplex modulusának hőmérsékletfüggését nehezen érthetjük meg, de biztosan nem elemezhetjük, vizsgálhatjuk termo dinamikai ismeretek hiányában. A hazai, de általában az építőmérnöki képzésnek nem része a fizikai kémia, ezen belül a termodinamika.
Az aszfaltkeverékekről minden építőmérnök tudja, hogy tulajdonsága függ a hőmérséklettől – termo plasztikus -, ezen belül adott hőmérsékleten a viselkedése viszkoelasztikus.
Ha egy anyag hőmérsékletfüggését meg akarjuk határozni, akkor tisztázni kell, hogy mit is értünk hőmérsékleten, mi a hőmérséklet?
A válasz egyszerűnek tűnik, hiszen minden nap mérjük, érzékeljük, tapasztaljuk, ha azonban az egzakt választ akarunk adni, akkor rájöhetünk, hogy egy jelentős problémával állunk szemben. 1992-ben a kiváló magyar származású fizikus [15] előadást tartott a hőmérsékletről, ahol ugyan nem oldotta meg a problémát, de egy kicsit ironikusan megállapította, hogy „A hőmérséklet csak egy érzés, egy érzéki percepció”. Természetesen ő is a hőmérsékletet a termodinamika alapmennyiségének tartja „A hőmennyiség nem más, mint a hőmérséklet és az entrópia változás szorzatának integrálja.”
Kürti előadásában [15] egy nagyon fontos dologra hívta fel a figyelmet „a termodinamikai hőmérsékleteket mindig, mint arányokat definiáljuk, sohasem különbségekként, „Alacsony hőmérsékleteknél azonban nem szabad elfelejteni, hogy csak a hőmérsékleti arányok számítanak.”
A hőmérsékletre vonatkozó egzakt kérdésre azonban nincs egzakt válasz, a válaszok kimerülnek a hőmérséklet mérésének és skálázásának leírásában.
A hőmérséklet mérése a tökéletes gázok viselkedésén alapul, amikor a viselkedés nem függ a gáz anyagi minőségétől. A tökéletes gáz \( pV_m \) nyomásának és moláris térfogati szorzatának változása arányos a hőmérséklet változásával. Az arányossági tényező az R, az egyetemes gázállandó.
A Celsius fokon kifejezett hőmérsékleti skála ez előzőek alapján:
\[ t=\frac{pV_m}{R}-T_0 \]
ahol:
\( p \) – nyomás (Pa) vagy (J/ m3)
\( V_m \) – moláris térfogat (dm3 *mol-1)
\( R \) – egyetemes gázállandó 8,315 (J *mol-1*K-1)
\( T_0 \) – abszolút nulla hőmérséklet -273,15 (oC)
Bármely gáz moláris térfogata 25 °C hőmérsékletre vonatkozó standard állapotában 24,5 dm3/mol, 0 °C hőmérsékletre vonatkozó normál állapotában 22,41 dm3 /mol.
A hőmérséklet mérése a hőtáguláson alapul. Ha egy \( \alpha \) lineáris hőtágulási együtthatóval rendelkező anyagú V0 térfogatú test hőmérséklete \( T_0 \) akkor \( ∆T=Tk-T0 \) hőmérséklet-változás hatására a térfogata:
\[ V_k=V_01+α∆T3 \]
A (8) egyenlet alapján akár azt is mondhatjuk, hogy a test a hőmérséklet hatására megváltoztatta a térfogatát, de ez így nem teljesen egzakt. A test a térfogatát azért változtatta meg, mert a testet felépítő részecskék mozgási, kinetikai energiája megváltozott. A test részecskéi állandóan rezegnek, forognak, ütköznek egymással. Minél nagyobb a testet alkotó részecskék átlagos mozgási energiája annál nagyobb a mért hőmérséklet. Valójában a testet alkotó részecskék átlagos mozgási energiájának változásából képzünk hőmérsékletet a (7) és (8) egyenletek alapján, ahol (7) az ideális gázokra vonatkozó összefüggés a hőmérséklet pontos mérésére alkalmazzuk.
A hőmérséklet mérésének kulcskérdése, az arányossági tényezőként használt R egyetemes gázállandó. Az egyetemes gázállandó felírható az Avogadro-szám és a \( k_B \) Boltzmann-állandó szorzataként:
\[ R=N_a\ast k_B \]
ahol:
\( k_B \) – Boltzmann állandó 1,380649·10−23 J/K
\( N_a \) – Avogadro-konstans 6,02217046⋅1023 db/mol
Azonos nyomás, hőmérséklet és térfogat esetén minden ideális gáz ugyanannyi gázmolekulát tartalmaz, 1 mol, \( V_m \) moláris térfogatban pontosan \( N_a \) db részecske található.
A Boltzmann-állandó \( (k_B) \) a test hőmérséklete és az azt felépítő részecskék mozgási energiája közötti kapcsolatot adja meg. 1 foknyi hőmérséklet-emelkedés esetén valamely gáz minden molekulája szabadságfokonként átlagosan \( 1/2 k_B \) energiát vesz fel, vagyis a gáz egy molja \( {\frac{3}{2}N}_ak_B=\frac{3}{2}R \) energiát vesz fel hőmérsékleti fokonként.
A Boltzmann állandó egyetlen darab elemi részecskére vonatkozik, pl. 1 db molekula.
A Boltzmann állandó szilárdtest-fizikai összefüggések alapján, az elektromosság makrofizikai mennyiségeinek mérésével is meghatározható, amellyel igazolható az állandó univerzális jellege. Az univerzalitást igazolja a Stefan-Boltzmann-féle üregsugárzási törvény is.
A Boltzmann-állandóból következik az ekvipartíció-tétel, amely egy rendszer hőmérséklete és az általános energiája között teremt összefüggést, ami az építőmérnöki gyakorlatban ellentmondás nélkül használható. Az ekvipartició felhasználásával a Boltzman eloszlás megadja, hogy a részecskék, molekulák milyen hányada rendelkezik egy megadott \( E_i \) küszöbenergiánál nagyobb kinetikus energiával.
\[ f_i={e\ }^{\left(\frac{-E_i}{RT}\right)} \]
ahol:
\( f_i \) – azon molekulák aránya, amelyeknek kinetikus energiája meghaladja a megadott \( E_i \) küszöbenergiát,
\( E_i \) – a megadott \( E_i \) küszöbenergia szint (J)
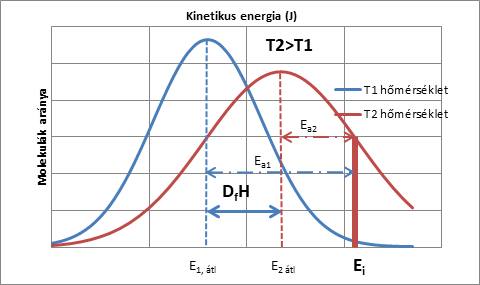 |
A 2. ábra szerinti Boltzmann-féle eloszlást használhatjuk folyadékok esetén is, sőt olyan folyadékoknál is, amelyek több, akár többszáz eltérő tulajdonságú molekulából állnak, mint a bitumen. A 2. ábrán látható két eltérő hőmérsékletű anyag energia eloszlása. Ha egy anyag állapotát az átlagos energiájával jellemezünk \( E1,átl \); \( E2,átl \), akkor egy adott hatás eléréséhez, pl. folyáshoz, töréshez szükséges energiát \( E_a \) aktiválási energiának nevezzük. Az aktiválási energiát a kívánt hatás eléréséhez megadott \( E_i \) küszöbenergia és az anyag átlagos \( Eátl \) energiájának különbségeként értelmezzük, a 2. ábra szerint \( E_{a,1} \); \( E_{a,2} \).
Folyás és törés kialakulásához a molekuláknak egymáshoz képest egy adott távolságot kell elérnie, amit nemcsak a hő növelésével, hanem külső erővel is elérhetünk. Rezgő rendszerek esetén ezt a távolságot hő esetén az A amplitúdó jellemzi, míg külső erő hatására –impulzus- a fajlagos alakváltozás \( \varepsilon \). Együttes hatáskor az amplitúdó és a fajlagos alakváltozás összeadódik, de az amplitúdó skaláris – minden irányban azonos az átlagos amplitúdó értéke -, míg a fajlagos elmozdulás vektor.
Mint később látni fogjuk a komplex modulus, vagy a viszkozitás hőmérsékleti függését jelentősen befolyásolja a vizsgálat közben lejátszódó olvadás vagy párolgás. E miatt röviden tárgyalni kell a bitumen olvadását, kristályosodását, valamint párolgását.
Az olvadék akkor kezd kristályosodni, ha az olvadékban rendezetlen mozgást végző atomok, molekulák a kristályrács rendezettségének megfelelő helyzetbe jutnak és kristálygócok keletkeznek.
A bitument alkotó molekulák mérete olyan változékony és bonyolult szerkezetű, hogy az útépítési alkalmazási hőmérsékleti tartományban a kristályosodás valószínűsége viszonylag alacsony.
A bitumen belső súrlódása – viszkozitása – a hűtés során a molekulák eltérő kinetikus energiájának következtében fokozatosan változik, növekszik.
A Boltzmann-féle energiaeloszlás szerint adott T hőmérséklet mellett van annak valószínűsége, hogy több molekulának az energiája a kristályosodáshoz szükséges szintre csökkenjen. A kristályosodáshoz azonban, a kvantummechanika szabályait is figyelembe vevő legalább n darab azonos tulajdonságú és megfelelő energiaszintű molekulának kellene egymás mellett elhelyezkedni, hogy érvényesüljön a korrespondenciaelv szerinti klasszikus fizika törvényszerűsége. A kristályosodás valószínűségét tovább csökkenti, hogy a hőtranszport egy dinamikus folyamat, amely növeli és csökkenti az adott lokális terület energiaszintjét.
Bitumen estén azonban a kristályosodás valószínűségét egyedi módon kell elemezni. Előfordulhat, hogy a bitumenbe térfogatarányosan nagy mennyiségű viszonylag magas hőmérsékleten kristályosodó anyagot pl. viaszt keverünk, amely anyag a mennyiség függvényében már kristályosodhat.
Az aszfaltkeverékek vizsgálata során általában nem számolunk a szilárd anyag olvadáshőjével -30 oC-tól +60 oC közötti hőmérséklettartományban, nagymennyiségű viasz esetén már számolni kellene az olvadáshővel.
A másik fázisátmenet a párolgás, amely folyamat a hőmérséklet megváltozása nélkül növeli az entrópiát. Az aszfaltkeverékek ill. egyéb anyagok hőmérsékletfüggő mechanikai vizsgálatánál kerülni kell a vizsgálat közbeni párolgást, ezért a vizsgálati minta temperálását minden esetben „szárazon” a légkamrában kell végezni. Egyszerűbb lenne, mint pl. a betonok esetén a vízben történő temperálás, de aszfaltkeverékek esetén a párolgás miatt keletkező entrópia növekedés megváltoztatja az aszfaltkeverék adott hőmérsékleten mért mechanikai tulajdonságát, komplex modulusát. Betonok esetén is növekszik az entrópia a párolgás miatt, de az így keletkezett belső energianövekedés nem elegendő a beton mechanikai tulajdonságának, komplex modulusának mérhető, a gyakorlati felhasználást befolyásoló változásához. A beton komplex modulusának változásához szükséges \( E_{beton} \) aktiválási energia sokkal magasabb, mint az aszfaltkeverék komplex modulusának változásához szükséges \( E_{aszfalt} \) aktiválási energia.
\( E_{beton}\gg E_{aszfalt} \)
Az aszfaltkeveréket a Föld légkörének hőmérsékleti tartományán belül hőmérséklet függőnek nevezzük, míg a betont nem tekintjük hőmérsékletfüggőnek.
Természetesen a fizikai és a kémia, vagyis a természeti törvények szerint minden anyag mechanikai tulajdonsága hőmérsékletfüggő, érvényesek a termodinamika törvényei.
Az aszfaltkeverékek a bitumenen kívül 80 térfogatszázalék körüli ásványi anyagokat is tartalmaznak, amelyek minden esetben szilárdak és kristályos szerkezetűek, ezért fizikai tulajdonságaik irányfüggőek. A bitumen és az ásványi anyagok közötti adhéziót döntően a van der Waals-féle erők biztosítják. A dipólus-dipólus és a diszperziós hatás független a hőmérséklettől, míg a dipólus-indukált dipólus hatás hőmérsékletfüggő.
A dipólus-indukált dipólus hatás általában nem jelentős, de hőmérsékletfüggése miatt hatással van az aszfaltkeverék komplex modulusának hőmérsékletváltozására.
A Newtoni folyadékok viszkozitásának hőmérsékleti függésének vizsgálatánál felhasználható a 2. ábra szerinti Boltzmann-eloszlás, ahol az \( E_i \) a viszkózus folyás állapotába került molekulák arányát határozza meg különböző hőmérsékleten. Az \( E_i \) nevezhetjük a viszkózus folyás aktiválási entalpiájának is.
Az entalpia az állandó nyomáson végzett vizsgálatokat, folyamatokat jellemzi, ahol a vizsgált test belső energiájának változását kizárólag a hő okozza.
Építőmérnöki gyakorlatban az aszfaltkeverék, vagy a bitumen vizsgálatokat általában adott hőmérsékleten és légköri nyomáson végezzük. A vizsgálatok során terheljük a próbatesteket, aminek következtében a testben feszültségek és alakváltozások keletkeznek. A vizsgálatok során, különösen a dinamikus vizsgálatoknál a próbatest belső energiája folyamatosan változik.
A \( T_1 \) hőmérsékleten egyetlen terhelés hatására létrejövő az egész testben létrejött belső elemi munkát, energiát \( {(L}_b^{T_1}) \) a test térfogatára kiterjesztett határozott integrál adja:
\[ L_b^{T_1}=-\iint_{\left(V\right)\left(\varepsilon\right)}{\underline{\sigma}}^\ast d\underline{\varepsilon}\ d\underline{V\ } L_b^{T_1}=-\int_{\left(V\right)}{(\sigma}_xd\varepsilon_x+\sigma_yd\varepsilon_y+\sigma_zd\varepsilon_z)dV \]
Az \( L_b^{T_1} \) belső energia egyezik a terhelés \( L_k^{T_1} \) során végzett munkával, amit viszonylag egyszerűen a vizsgálattól függően tudunk meghatározni. A külső munka mindig állandó, ha a terhelés impulzusa állandó.
Amikor pl. az aszfaltkeverék komplex modulusának hőmérsékletfüggését vizsgáljuk különböző hőmérsékleteken, és frekvenciákon, akkor biztosítani kell, hogy a vizsgálat során a terhelés által keletkező belső kinetikus energia a hősugárzás által a vizsgálat előtti belső energiaszintre csökkenjen. Ezért kerülendő a terhelési ciklusszám növelése, és megfelelő hűlési időt kell biztosítani a frekvenciavizsgálatok között.
Ha nincs megfelelő idő a terhelések között, akkor a kritikus helyeken, a hő felhalmozódik, mert nincs idő a kiegyenlítődésre. A felhalmozott hő nem más, mint a részecskék, molekulák kinetikai energiájának növekedése, ami adott energiaszinten folyást, törést okozhat. Törés esetén a kémiai kötések „felszakadnak”, folyás esetén a molekulák egy másik stabil helyzetbe kerülnek, ami hőfelszabadulással jár.
A különböző hőmérsékleten mért komplex modulusok összehasonlítása termodinamikai szempontból akkor megfelelő, ha a próbatest részecskéinek, molekuláinak kinetikus energiaváltozását kizárólag a hőmérsékletváltozás okozza.
A komplex modulus mérése mechanikai módszerrel csak úgy végezhető el, ha a testen belüli molekulák kinetikai energiáját megváltoztatjuk. A vizsgálat során keltett kinetikai energia elhanyagolható az 1 oC hőmérséklet növekedéshez szükséges energiához képest.
Egy 4000 MPa komplex modulusú 1 dm3 aszfaltminta 0-ról 1,0 MPa-ra állandó sebességű felterheléséhez 0,125 J energia szükséges, míg az aszfalthabarcs 1 oC hőmérséklet-növeléshez szükséges energia [16] 950 J/(kgoC) fajlagos hőkapacitás esetén ~2400 J. Más szerzők szerint az aszfaltkeverékek fajlagos hőkapacitása 1000-2000 J/(kgoC) között várható [17].
A tanulmányban Q hőnek az energiatranszport által átadott energiát értem. Adott mennyiségű hő hatására a különböző anyagokban eltérő a hőmérséklet változása. Az átadott hő és a hőmérséklet-változása közötti kapcsolatot a hőkapacitás biztosítja.
Azt a hőmennyiséget, amely a rendszer hőmérsékletét 1 Kelvinnel emeli, anélkül, hogy belső átalakulás következne be, hőkapacitásnak nevezzük.
A hő (12), (13) a hőkapacitás hőmérséklet szerint határozott integrálja 3. ábra.
Állandó nyomásra vonatkozó hő \( T_1 \)-ről \( T_2 \) hőmérsékletre változásnál.
\[ Q_p=n\int_{T_1}^{T_2}{C_{mp}\left(T\right)dT} \]
Állandó térfogatra vonatkozó hő T_1-ről T2-re hőmérsékletre változásnál.
\[ Q_V=n\int_{T_1}^{T_2}{C_{mV}\left(T\right)dT} \]
ahol:
\( Q \) – hő (J)
\( C_{mp} \) – moláris hőkapacitás \( J\ {{mol}^{-1}K}^{-1} \), állandó nyomáson
\( C_{mV} \) – moláris hőkapacitás \( J\ {{mol}^{-1}K}^{-1} \), állandó térfogaton
\( n \) – anyagmennyiség
Az állandó nyomáson vett hőkapacitás mindig nagyobb, mint az állandó térfogaton, szilárd anyagok, aszfaltkeverékek, bitumen esetén a különbség elhanyagolható.
A fajlagos hőkapacitás esetén a hőkapacitást egységnyi tömegre vonatkoztatjuk, amelynek mértékegysége \( (J\ {kg}^{-1}K^{-1}) \).
Az anyagok hőkapacitás-függvényei általában nem lineárisak, de hatványsorok segítségével (14) megadható a hőkapacitás adott anyagra vonatkozó hőmérsékletfüggése.
\[ C_{mp}\ \left(T\ \right)=a\ +bT+cT^{-2}+dT^3+\ldots \]
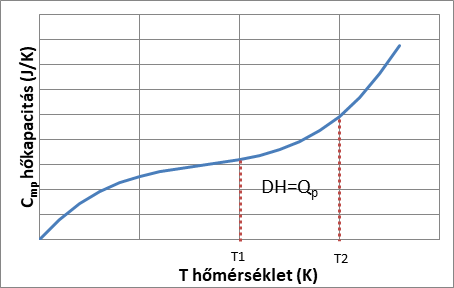 |
A mérnöki gyakorlatban a hőkapacitásra a \( T_1-\ T_2 \) hőmérsékleti tartományban van szükségünk, a dT^3 és a további tényezők elhanyagolása mellett a (14) integrálása után kapjuk a (15) egyenletet, amit sok esetben a szükséges paraméterek csökkentésének érdekében (16) és (17) egyszerűsíthetünk még megfelelően pontosság mellett. A (16) megfelel a vizsgálati eredményeknek [16, 17].
\[ \int_{T_1}^{T_2}{C_{mp}\left(T\right)dT}=\left(\ \alpha\left(T_2-T_1\right)^2+\beta\left(T_2-T_1\right)+\gamma+\delta\frac{\left(T_2-\ T_1\right)}{T_2T_1}\right) \]
\[ \int_{T_1}^{T_2}{C_{mp}\left(T\right)dT}=\left(\ \alpha\left(T_2-T_1\right)^2+\beta\left(T_2-T_1\right)+\gamma\right) \]
\[ \int_{T_1}^{T_2}{C_{mp}\left(T\right)dT}=\left(\gamma+\delta\frac{\left(T_2-\ T_1\right)}{T_2T_1}\right) \]
A (17) csak közelítő számításhoz, becsléshez alkalmazható.
Az entalpia \( \Delta H \) egy olyan állapotfüggvény, amely az állandó nyomáson lejátszódó folyamatok jellemzésére alkalmas, és állandó nyomás mellett a megváltozása egyenlő a hővel, \( \Delta H=Q_p \).
Ha a \( T_1-\ T_2 \) hőmérsékleti tartományban a vizsgált anyag egyik i. összetevője kristályosodik, akkor számolni kell ennek az i. anyagnak az olvadási \( H_o^i \) entalpiájával is. Aszfaltkeverékek esetén a párolgással nem számolunk.
\[ \Delta H=Q_p+\Delta H_o^i \]
Folyadékokban 2. ábra egy molekulának a helyváltoztatásához vagy egy új egyensúlyi helyzetbe kerüléshez az átlagos energiaszinttől magasabb energiaszintre van szüksége.
Az új egyensúlyi helyzetbe kerüléshez szükséges \( E_i \) küszöbenergia és az \( Eátl \) átlagos energiaszint közötti különbséget nevezzük \( E_a \) aktiválási energiának.
\[ E_a=E_i-Eátl \]
ahol:
\( E_a \) – aktiválási energia (J* mol-1)
A folyadékokban és a szilárd testekben minden részecske, molekula az egyensúlyi helyzete körül a hőenergiával arányosan rezgőmozgást végez, az energia eloszlását 2. ábrán szemléltetett Boltzmann-féle eloszlás adja.
A vizsgált test hőmérsékletének változtatása változó hőt, így változó kinetikai energiát okoz. A kinetikai energia változását a részecskék, molekulák sebességének négyzetes változása jellemzi. A részecskék, molekulák a rezgőmozgás során kölcsönhatásba kerülnek szomszédjukkal, ütköznek.
Az ütközések következtében kitérhetnek eredeti egyensúlyi helyzetükből és a szomszédjukban lévő „szabad térfogatba” ugorhatnak át. A szabad térfogat a hőmérséklet növekedése (8) miatt növekszik, ami növeli az új egyensúlyi helyzet kialakulásának valószínűségét.
A szabad térfogatra vonatkozó lineáris egyenletet [18] vezette be:
\[ \eta=\frac{1}{V-V_0} \]
Ahol:
\( V \) -folyadék térfogat
\( V_o \) – van der Waals térfogat, ahol már nem lehetséges a folyás
\( \eta \) – viszkozitás (Pa s)
(Cohen, 1959) [19] elméletileg levezetett pontosabb exponenciális egyenlet alkalmazását javasolta:
\[ \eta=A^{pre}\ e^\frac{V_0}{V-V_0} \]
A molekulának azonban nemcsak szabad térre, hanem megfelelő energiára is szüksége van a helyváltoztatáshoz, amely végül is elvezetett a (22) alkalmazásához, amit szokás (Arrhenius, 1889) egyenletnek is hívni:
\[ \eta=A^{pre}\ e^{\left(\frac{-E_a}{R\ T}\right)} vagy logaritmizálva \ln{\left(\eta\right)}=\ln{\left(A^{pre}\right)}+\frac{{-E}_a}{R\ T} \]
Az \( e^{-EiRT} \) kifejezés – Boltzmann eloszlás- adja meg a molekulák azon hányadát, melyek kinetikai energiája egy adott hőmérsékleten egyenlő vagy nagyobb a viszkózus folyáshoz szükséges \( E_i \) küszöbenergiánál.
(Messaadi, et al., 2015) és munkatársai [20] 34 db Newtoni folyadék viszkozitásának meghatározásához szükséges paramétereket számították a (22) egyenlet felhasználásával, ami igazolja, hogy a viszkozitást nemcsak empirikus, hanem termodinamikai alapon is meg lehet határozni.
Folyékony fémek esetén [21] igazolták, hogy a nagy szabad térfogat nem feltétlen szükséges a diffúziós változáshoz, mivel a vizsgált fémekben a szabad térfogat csak 10%-a volt az atom térfogatának. Kimutatták a diffúzió folyamatának láncszerű jellegét, ahol legalább tíz atom mozog kismértékben. Továbbá igazolták, hogy a folyékony fémekben az atomi kötések nagy sebességgel szakadnak és képződnek. A diffúzió az anyagáramlást jellemzi \( (m^2/s) \), ami arányos a viszkozitással.
Aszfaltkeverékek vizsgálatakor a diffúzióval közvetlenül nem, csak a viszkozitáson, komplex moduluson keresztül közvetve foglalkozunk. Ha azonban a diffúzióhoz nem szükséges jelentős szabad térfogat, akkor a viszkozitás változásához se kell.
Viszkozitás és a komplex modulus meghatározása termodinamikai alapon
Gyakran arra keressük a választ, ha ismerjük \( T_1 \) hőmérsékleten a \( \eta_1 \) viszkozitás értékét, akkor \( T_2 \) hőmérsékleten mekkora lesz a \( \eta_2 \) viszkozitás értéke 2. ábra.
Megfogadva [15] tanácsát, arányokat keresünk. A 2. ábra szerint értelmezve az aktivációs energiákat és hőmérsékleteket kapjuk a (23) egyenletet.
\[ \eta_1=A^{pre}(T){\ e}^{\left(\frac{E_{a2}-E_{a1}}{RT_1\ }\right)}; \eta_2={A^{pre}(T)\ e}^{\left(\frac{E_{a2}-E_{a1}}{RT_2\ }\right)}; \frac{\eta_1}{\eta_2}={\ e}^{\frac{-1}{R}\left(\frac{E_{a1}}{T_1\ }-\frac{E_{a2}}{T_2\ }\right)}
\eta_1=\eta_2 e-^{1R∆fHT2- T1T2T1} \]
Ha nincs fázisátalakulás a \( T_1-\ T_2 \) hőmérséklet tartományban, akkor a ∆fH teljes egészében számítható a vizsgált anyag által felvett \( Q_p \) hővel. A \( Q_p \) hő a (12) egyenletből határozható meg, ha ismerjük az anyag hőkapacitásának hőmérsékleti függését (14) a \( T_1-\ T_2 \) hőmérsékleti tartományban.
A 2. ábrán a két azonos tulajdonságú, de eltérő hőmérsékletű anyagot hasonlítunk össze. A \( T_2 \) hőmérséklet esetén az anyagot az E2,átl átlagos energiával jellemezzük, amely energia állapothoz a \( \eta_2 \) viszkozitás tartozik, ezt mértük \( T_2 \) hőmérsékleten és adott frekvencián.
A \( T_1 \) hőmérsékleten az E1,átl átlagos energiát a \( \eta_1 \) viszkozitás jellemezi. A két állapot közötti átlagos energia eltérését a hőmérséklet változása miatti \( ∆fH \) entrópia változása jellemzi.
Azt azonban nem szabad elfeledni, hogy a viszkozitást, ill. a komplex modulust általában mechanikai módszerekkel mérjük.
A (22) egyenleten belül a \( ∆fH \) entrópiváltozás azt a belső energiaváltozást jelenti, amely energia szükséges a \( \eta_1 \) viszkozitásról \( \eta_2 \) viszkozitásra változáshoz. Ebben az esetben az elérendő hatás a \( \eta_2 \) viszkozitás elérése. A \( \eta_2 \) viszkozitást úgy értük el, hogy a \( T_1 \) hőmérsékletet \( T_2 \)-re változtattuk. A \( T_2 \) hőmérsékletű és \( \eta_2 \) viszkozitású anyag E2,átl átlagos energiája lett a kívánt hatáshoz szükséges \( E_i \) küszöbenergia, ebben az esetben a 2. ábra szerinti \( ∆fH \) entrópiaváltozás egyezik az \( E_a \) aktivációs energiával.
A \( T_1-\ T_2 \) hőmérséklet tartományban az entalpia változása egyezik állandó nyomáson avval a hőmennyiséggel, amit a (12) egyenlet szerinti a \( T_1-\ T_2 \) hőmérséklet változása okoz a vizsgált testben, vagyis \( ∆fH=Qp \), ezért felírható a (24) egyenlet.
\[ \eta_1=\eta_2{\ e}^{-\left[\frac{\left(T_2-\ T_1\right)}{R\ T_2T_1}\int_{T_1}^{T_2}{C_{mp}\left(T\right)dT}\right]} \]
A (24) egyenlet nemcsak a viszkozitásra, hanem a komplex modulusra is alkalmazható. Aszfaltkeverékek hőkapacitásának a (16) egyenlet már igen nagy pontosságot biztosít, ennek megfelelően a komplex modulusra felírhatjuk:
\[ {EK}_1={EK}_2{\ e}^{-\left[\frac{\alpha\left(T_2-T_1\right)^3+\beta\left(T_2-T_1\right)^2+\gamma\left(T_2-T_1\right)}{R\ T_2T_1}\right]} \]
ahol:
\( {EK}_1 \) – komplex modulus T_1 hőmérsékleten (MPa)
\( {EK}_2 \) – komplex modulus T_2 hőmérsékleten (MPa)
\( \alpha \); \( \beta \); \( \gamma \) – illesztési paraméterek, vagy a moláris hőkapacitás paraméterei.
Fontos megjegyezni, hogy a moláris hőkapacitás paraméterit nem mérjük, hanem iterációval számítjuk a mért komplex modulus értékekből, ennek pedig az lesz a következménye, hogy az illesztési paraméterek értékét befolyásolja a később tárgyalt referencia hőmérséklet is.
A (25) a terhelés frekvenciájától független egyenlet. A komplex modulust és a viszkozitást azonban a terhelés frekvenciája is befolyásolja, amely hatást a következő fejezetben tárgyalom. Egy adott, felvett vagy mért frekvencián a (27) szerint számított \( {EK}_1 \) komplex modulust fogom a terhelés által keltett frekvenciára átszámítani.
Amikor az építőmérnöki gyakorlatban viszkozitást, nyírási modulust vagy komplex modulust mérünk, akkor egy külső erő hatására bekövetkező, adott viszonyítási ponthoz képest a test pontjainak térbeli elmozdulásait vizsgáljuk. A test pontjainak, molekuláinak mozgását tömegpontjukkal jellemezzük, amely tömegpont adott amplitúdóval és frekvenciával rezeg a tér minden irányába azonos valószínűséggel. A mért elmozdulás a rezgési középpontok elmozdulásainak összegeként értelmezhető.
Külső erő hatására a vizsgált test molekulái egymáshoz képest is elmozdulhatnak, amely tartós alakváltozást okoz a vizsgált testben, az alakváltozás a terhelés megszűnése után is megmarad.
Rugalmas alakváltozásról akkor beszélünk, amikor a külső erőhatás megszűnése után a molekulák visszatérnek a terhelés előtti eredeti helyzetükbe. Az ilyen viselkedésű anyagokat nevezzük ideálisan rugalmas anyagoknak. Ilyen anyag azonban nem létezik, mert miden anyag csak adott hőmérsékleti tartományban viselkedik közelítően rugalmasan pl. gumi, acél stb.
A terhelés során a molekulák egy része hőmérséklettől, terhelési frekvenciától és a molekulák közötti kötési energiától függően olyan mértékű elmozdulást szenvednek el, amelynek során a kötőerők felszakadnak és egy új stabil állapotba kerülnek, ahol új kötés alakul ki. A molekulák közötti kötőerőket az elektromos és mágneses mező határozza meg. A molekula ebben az új helyzetben, állapotban is rugalmasan viselkedik, de a terhelés megszűnésekor az új helyzetben marad, nem tér vissza a terhelés előtti állapotába. Attól függően, hogy milyen valószínűséggel kerülnek a molekulák egy új helyzetbe lesz egyre nagyobb a maradó alakváltozás.
A külső befektetett energia egy része, a maradó alakváltozással arányosan vissza nem nyerhető energiává alakul. Minél nagyobb a hőmérséklet, annál nagyobb a maradó alakváltozás valószínűsége, annál kisebb a viszkozitás 2. ábra. A Boltzmann-féle eloszlás következménye, hogy egy testen belül mindig van annak valószínűsége, hogy egy kémiai kötés felszakad. Egyes helyeken az amplitúdó annyira megnövekedhet, hogy az elemi részecske, molekula egy új stabil helyzetbe, állapotba kerül. Ha ez az állapot egy lokális helyen már „n” darab részecskét érint, akkor a test ezen a lokális helyen mérhető maradó alakváltozást szenved el.
A külső erő hatására az új helyzetbe került molekulák között ismét stabil kötések jönnek létre, amit a kialakuló elektromos és mágneses mező határoz meg.
A terhelés miatti molekulák közötti felszakadás és újrakötés, valamint a tartós felszakadás minden esetben együttesen jelentkezik, de eltérő valószínűséggel. A terhelés növekedésével a felszakadó kötések valószínűsége növekszik, és ezen belül növekszik a tartós felszakadás valószínűsége.
Tartós a „felszakadás”, ha az aszfaltkeverékben mikrorepedések keletkeznek.
A folyamat következménye, hogy a terhelés növekedésével a feszültség alakváltozás aránya eltér a lineáristól, az eltérés jelentőssé a törőszilárdság 70-80%-nál következik be [22].
Belső frekvencia-hőmérséklet összefüggése Arrhenius alapján
Evidenciának tekintjük, hogy (Arrhenius, 1889) (26) egyenletét a terhelés frekvenciája és a vizsgálati hőmérséklet közötti összefüggésre is lehet alkalmazni, az összefüggés igaz, de egyáltalán nem evidens.
Arrhenius 1889-ben Hoff-egyenletének [23] (Hoff, 1885) (27) felhasználásával általánosította empirikus megközelítését.
\[ {k=A^{pre}\ e}^{-\frac{E_a}{RT}}, vagy logaritmizálva: lnk=lnA^{pre}+\frac{{-E}_0}{RT} \]
A K egyensúlyi állandó hőmérsékletfüggését a van’t Hoff-egyenlet írja le:
\[ \frac{dln(K)}{dT}= \frac{-∆fH}{RT2}; ln\left(\frac{K_{T2}}{K_{T1}}\right)= \frac{-∆fH}{R} \frac{T2-T1}{T2T1} \]
ahol:
\( K_T \) – egyensúlyi állandó T hőmérsékleten
\( k \) – reakciósebességi állandó (mol/sec)
\( A^{pre} \) – preexponenciális tényező (mol/sec)
\( E_0 \) – aktiválási energia (J/mol)
\( R \) – egyetemes gázállandó 8,315 (J *mol-1*K-1)
A k a reakciót eredményező ütközések másodpercenkénti száma.
Az „\( A^{pre} \)” az ütközések teljes száma másodpercenként, az \( {\ e}^{-\frac{E_a}{RT}} \) pedig annak valószínűsége, hogy az ütközés reakciót vált ki, pl. a molekula egy új egyensúlyi helyzetbe kerül, ha „n” darab molekuláról van szó akkor a lokális helyen „folyás” következik be. Az „n” darab az a minimális molekulaszám, amikor már nem a kvantummechanika, hanem a klasszikus fizika érvényes.
Az \( „A^{pre}” \) preexponenciális tényező a részecskék ütközési gyakorisága, amely független a részecskék kinetikai energiájától.
\[ A^{pre}=z\ast f \]
ahol:
\( z \) – a másodpercenkénti ütközési szám (db/s)
\( f \) – sztérikus faktor f\le1,0 azon ütközések aránya melyek orientációja reakcióhoz vezet.
A gázkinetikus ütközési szám függ a hőmérséklettől, azonban az exponenciális hőmérséklet függés miatt ezt a hatást elhanyagolják és értékét a hőmérséklettől független állandó értékre szokták felvenni
Ha (26) Arrhenius egyenletétnél a \( k_{1;\ }T_{1\ } \) és \( k_{2;\ }T_{2\ } \) arányát képezzük, akkor (23) analógiára Hoff-egyenletét kapjuk, avval a különbséggel, hogy nem az egyensúlyi állandó hányadosát, hanem a reakciósebességi állandó hányadosát kapjuk eredményül.
Hoff-egyenletéből következik, ha (27) teljesül \( p_1 \) ; \( p_{2\ } \) külső nyomáson és \( T_1 \); \( T_2\ \) hőmérsékleten, akkor igaznak kell lennie a \( T_1 \); \( T_2 \) hőmérsékletváltozás miatt bekövetkezett belső energiaváltozásra \( \frac{U_2}{U_1} \) is, valamint a részecskék, molekulák átlagos sebességének négyzetes arányára is \( \frac{{v_2}^2}{{v_1}^2} \).
\[ \frac{K_{T2}}{K_{T1}}=\frac{k_2}{k_1}=\frac{U_2}{U_1}=\frac{{v_2}^2}{{v_1}^2}=h^2 \]
Arrhenius egyenlete azonban a test, gáz részecskéinek, molekuláinak sebességére, közvetetten belső frekvenciájára vonatkozik, a vizsgált testet ért terhelés frekvenciaváltozással nem foglalkozik.
Kristályos és folyékony anyagok esetén, a belső energia, felírható az x,y,z tengelyirányú kinetikai energiák összegeként, ahol a részecskék, molekulák rezgőmozgást végeznek. Molekulák esetén is a molekula mozgását minden esetben a molekula tömegpontjával jellemezzük és a mozgást erre a pontra értelmezzük. Ami különösen fontos az „óriás” molekulák esetén, ahol az óriásmolekula tömegrészeinek mozgási energiáinak összege egyezik a tömegpont teljes molekulatömegre vonatkozó energiájával.
\[ U=\frac{1}{2}\ m\ \left[\left(A_x\omega_x\right)^2+\left(A_y\omega_y\right)^2+\left(A_z\omega_z\right)^2\right] \]
ahol:
\( A_{x,y,z} \) – tengelyirányú amplitúdó (m)
\( \omega_{x,y,z} \) – tengelyirányú frekvencia (1/s)
\( m \) – tömeg (g)
Ha egy test állandó nyomáson van, akkor a belső energiaváltozás hőtranzport által valósul meg. Egy mólnyi anyag átlagos belső energiáját írja le a (30) egyenlet, ahol a sebesség – az átlagos amplitúdó és a frekvencia szorzata \( v=A\ \omega \) – minden irányban azonos valószínűségű, ezért felírható (31):
\[ U=\frac{3}{2}\ m\ \left(A\ \omega\right)^2 \]
A továbbiakban 1 mol tömeget vizsgálunk.
Az 1 mol tömegű anyag hőmérsékletét növeljük 1 oC-al, ekkor a részecskék átlagos v sebessége „h” szorosára fog növekedni, ez a „h” szerepel az (29) összefüggésben is.
Ne feledjük, a Boltzmann-állandó \( (k_B) \) a test hőmérséklete és az azt felépítő részecskék mozgási energiája közötti kapcsolatot adja meg. Egy foknyi hőmérséklet-emelkedés esetén valamely gáz minden molekulája szabadságfokonként átlagosan \( 1/2 k_B \) energiát vesz fel, vagyis a gáz egy molja \( {\frac{3}{2}N}_ak_B=\frac{3}{2}R \) energiát vesz fel.
Az energiaeloszlást a 2. ábra szemlélteti, amely a sebességeloszláson alapul.
A hőmérsékletváltozás miatt megváltozott \( ∆U \) belső energia a (31) miatt \( ∆v \) sebességváltozással jár. A sebesség változását okozhatja az A amplitúdó és a \( \omega \) frekvencia változása is. Állandó nyomáson az amplitúdónak is változnia kell a hőtágulás (8) alapján.
Arrhenius egyenlete nem a belső frekvencia, hanem a részecskék v sebessége és a hőmérséklet változása közötti összefüggésre vonatkozik, ezért se evidens a külső frekvencia változása és a hőmérséklet változása közötti összefüggés.
A (27) egyenlet közelítő pontosságú, mivel a folyamat entalpia- és entrópia változását a hőmérséklettől függetlennek tételezi fel. Az egyenletet főként annak becslésére használják, hogy más hőmérsékleten mennyi lesz az egyensúlyi állandó új értéke. Pontosabb értéket akkor kapunk, ha a \( ∆fH \) entalpiaváltozásnál figyelembe vesszük a hőkapacitás (16) szerinti hőmérsékletfüggését (32).
\[ k_1=k_2{\ e}^{-\left[\frac{\alpha\left(T_2-T_1\right)^3+\beta\left(T_2-T_1\right)^2+\gamma\left(T_2-T_1\right)}{R\ T_2T_1}\right]} \]
A (26) egyenlet a logaritmizált alakja szerinti 4. ábrán láthatjuk a belső frekvencia és a hőmérséklet összefüggését, ahol az Arrhenius szerinti iránytangens \( \frac{{-E}_a}{R} \), ha figyelembe vesszük a hőkapacitás (16) hőmérsékletfüggését is, akkor már nem egy egyenest, hanem egy a négyzeteshez közeli, de sok esetben egy harmadfokú görbét kapunk.
 |
A (26) egyenlet átalakításával a \( T_1-\ T_2 \) hőmérséklet tartományban, ahol \( k_1 \) a \( T_1 \) hőmérséklethez tartozó frekvencia, míg \( k_2 \) a \( T_2 \) hőmérséklethez tartozó frekvencia kapjuk az (33) Arrhenius-féle egyenletet:
\[ k_1=k_2e^{\frac{-1}{R}\left(\frac{E_a\left(T_2-T_1\right)}{\ T_2T_1}\right)} \]
Arrhenius egyenletében az aktivációs energia \( E_a=∆fH \) megegyezik az entrópia változásával.
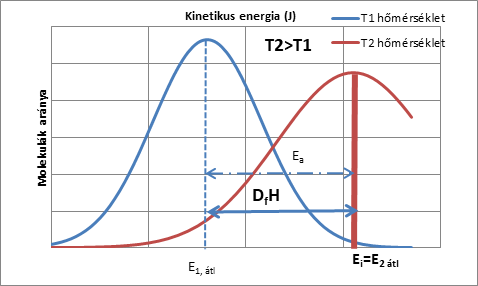 |
A (32) egyenletben szereplő reakciósebességek aránya egyezik a (24) viszkozitások arányával, ami szükségszerű, hiszen a viszkozitás változását a reakciósebességet meghatározó kinetikai energia változása okozza, teszi lehetővé. Mindkét esetben ugyan arról van szó a test részecskéinek, molekuláinak sebessége változik.
Arrhénius-féle egyenletében csak a belső hőenergia, entalpiaváltozás miatti kinetikai energia változása szerepel a terhelés frekvenciájának változása nem.
Hőmérséklet és a terhelés frekvenciájának összefüggése
Mindeddig a test részecskéinek, molekuláinak a test hőmérsékletének változása miatti sebességváltozásával foglalkoztunk.
A (4); (5); (6) eltolási függvényekkel azt szeretnénk biztosítani, hogy az 5. ábra szerinti \( T_1 \) hőmérsékleten és \( f_1 \) frekvencián, valamint \( T_2 \) hőmérsékleten és \( f_2 \) frekvencián is azonos értékű \( {EK}_1=\frac{\sigma_1}{\varepsilon_1} \) komplex modulust mérjünk. Hasonlóképpen elvárjuk, hogy \( T_2 \) hőmérsékleten és \( f_1 \) frekvencián, valamint \( T_1 \) hőmérsékleten és \( f_1 \) frekvencián is \( {EK}_2=\frac{\sigma_2}{\varepsilon_2} \) komplex modulus mért értékének azonosságát.
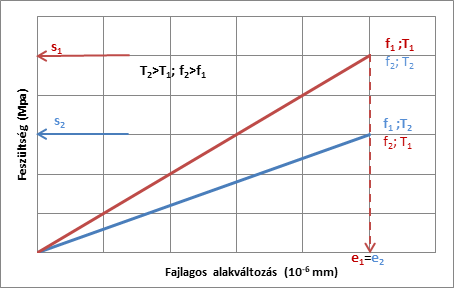 |
Az 5. ábra szerinti értelmezésben mindegy, hogy a komplex modulus mérést \( f_1 \) frekvencián és \(T_1 \) hőmérsékleten, vagy \( f_2 \) frekvencián és \(T_2 \) hőmérsékleten végezzük.
Az 5. ábra szerinti feszültség-fajlagos alakváltozás lineáris viselkedés kizárólag állandó terhelési frekvencia és hőmérséklet esetén teljesül. Egyetlen felterhelés esetén pl. 0-ról \( \sigma_1 \) feszültségre nem teljesülhet, mivel a frekvencia függ a terhelési időtől, ezért a felterhelés során a frekvencia folyamatosan változik. A tervezett frekvencia kizárólag egy ponton pl. az \( \varepsilon_1 \) fajlagos alakváltozás elérésekor biztosítható. Az 5. ábra szerinti lineáris összefüggést több mérésből úgy kapjuk, hogy minden egyes fajlagos megnyúlás értékre a felterhelést azonos \( t_i=\frac{2\pi}{f_i} \) felterhelési idővel végezzük el, ahol \( f_i \) a terhelési frekvencia.
Ez esetben azt mondjuk, hogy a vizsgálati erőteret a \( T_i \) hőmérséklet és az \( f_i \) frekvencia jellemzi, ami nem más, mint az útpályaszerkezet erőterének modellje, ahol a tehergépjárművek sebessége határozza meg a terhelési frekvenciát. A hőmérsékletet, amely paramétereket a tervezés során állandó, mértékadó értékre veszünk fel. Jelen cikkben nem foglalkozom az ilyen tervezés korlátaival.
A továbbiakban a számításokat és levezetéseket ebben a \( T_i \) hőmérséklet és az \( f_i \) frekvenciával jellemzett erőtérben végezem.
A komplex modulusra és a viszkozitásra vonatkozó vizsgálati eljárásokat úgy végezzük, hogy az egymásra merőleges főfeszültségek közül legalább kettő nulla értékű. A (11) egyenlet így egyszerűsödik egy adott V térfogatra.
\( ∆U=L_b^{T1}=-V∫_0^εσ_xdε_x \); amely lineáris esetben:
\( ∆Ux=V\frac{1}{2}σ_xε_x \)
A V térfogatra vonatkozó belső \( ∆U_x \) energia növeli a molekulák kinetikai energiáját, amely V térfogat és m tömeg esetén:
\[ ∆U_x=V\frac{1}{2}σ_xε_x=m\frac{3}{2}A_if_i^2 \]
A terhelésből származó ∆Ux kinetikai energiaváltozás elhanyagolható a hőmérsékletváltozáshoz szükséges energiaváltozáshoz képest, ezért ez a hatás nem befolyásolja érdemben az eltolási függvényt, amit a következő levezetéssel igazolom.
Az aszfaltkeverék fajlagos hőkapacitásának ismeretében (36) számítható az a \( Q_p \) hőmennyiség, amely az m tömegű aszfaltkeverék hőmérsékletének \( T_1 \)-ről \( T_2 \)-re változtatásához szükséges, ha nincs állapotváltozás.
\[ ∆Q_p=m \int_{T_1}^{T_2}c(T)dT \]
Ha igen kicsi hőmérsékletváltozást vizsgálunk, akkor:
\[ ∆Q_p=∆TC_mp(T)=∆Tmc \]
A \( ∆Q_p=∆U \) egyenlőségől számíthatjuk a keresett \( ∆T \) hőmérsékletkülönbséget.
\[ \sigma\varepsilon=\frac{3\rho}{2}c∆T; ∆T=\frac{2σε}{3ρc} \]
ahol:
\( \sigma \) – feszültség MPa; 106 kg m-1 s-2
\( ∆U \) – belső energia változás J; kg m s-2
\( f_k \) – terhelés körfrekvenciája s-1; Hz
\( \rho \) – sűrűség kg m-3, \( \rho=\frac{m}{V} \)
\( c(T) \) – fajlagos hőkapacitás J kg-1 K-1 vagy m2 K-1 s-2)
A számítást 20 oC vizsgálati hőmérsékleten \( \sigma =1,0 MPa \), \( EK=4000 MPa \); \( \rho=2500 kg m^-3 \) és c= 1000 J kg-1 K-1 esetre elvégezve, \( ∆T= 6,67 10-5 oC \), ami elhanyagolható a vizsgálatkor előírt +-0,3 C -hoz képest, amelyen az se változtat lényegesen, ha a testet törésig \( \sigma =5,0-10 MPa \)-ig terheljük.
Miután igazoltam, hogy a komplex modulus mérése nem vagy elhanyagolható mértékben növeli a vizsgálati hőmérsékletet, térjünk vissza az eltolási függvény számításához.
Az eltolási függvény meghatározásához viszonyítási pontnak vegyünk fel egy \( \varepsilon_i \) fajlagos megnyúlást. Feltételként fogalmazzuk meg, ami a jelenlegi mérési eljárásokban is előírás, hogy minden vizsgálati hőmérsékleten az \( \varepsilon_i \) fajlagos alakváltozás eléréséig a vizsgált anyagnak feszültség fajlagos alakváltozás összefüggés közel lineáris.
Az 5. ábra szerint az \( \varepsilon=\varepsilon_1=\varepsilon_2 \) fajlagos megnyúlás eléréséhez szükséges kinetikai energia \( T_i \) hőmérséklet és az \( f_i \) frekvencián a (34) szerint számoljuk, amely esetben teljesülnie kell az \( A=A_1=A_2 \), mivel a rezgések amplitúdóinak változása okozza a fajlagos megnyúlást, ezért, ha a fajlagos megnyúlás nem változik, akkor az amplitúdó se változhat.
Szilárd vagy folyékony anyag hőmérsékletének \( ∆T=T2-T1 \) változása esetén a \( ∆A \) amplitúdó változása a (8) egyenlet következtében, amikor az \( \alpha\left(T\right) \) hőtágulási együttható függ a hőmérséklettől (41). A rezgés \( ∆AA \) amplitúdójának fajlagos változása arányos a vizsgált test \( \varepsilon=∆ll \) fajlagos alakváltozásával.
Egy l hosszúságú rúd \( ∆l \) hőmérsékletváltozás miatti hőtágulása felírható a rúd hosszirányában elhelyezkedő n db molekula átlagos \( A(T_1) \) és \( A(T_2) \) amplitúdóinak különbségeinek összegeként is, aminek következménye (39).
\[ ∆l= \sum_{i=1}^{n} (A(T_2)-A(T_1)); ∆l=nA(T_1) \int_{T_1}^{T_2} \alpha (T)dT \]
\[ \alpha\left(T\right)=a_hT+b_h \]
ahol,
\( a_h \); \(\ b_h \) – az anyagra jellemző hőtágulási mérési állandók
Tájékoztatásul az aszfaltkeverék átlagos \( \alpha \) hőtágulási együtthatója \( ~2,5 10-5 \).
\[ \varepsilon=\frac{∆l}{l} = \frac{∆A}{A}= \int_{T_1}^{T_2} \alpha(T)dT \]
A \( T_1 \) hőmérséklet és az \( f_1 \) frekvencián a mért komplex modulus \( {EK}_1 \), míg \( T_2 \) hőmérséklet és az \( f_1 \) frekvencián a mért komplex modulus \( {EK}_2 \).
Az \( {EK}_1 \) és az \( {EK}_2 \) komplex modulusok aránya a (33) szerint, ahol \( {EK}_i=\sigma_i\varepsilon_i \)
\[ ∆U_1=V\frac{1}{2}EK_1ε^2=m\frac{3}{2}(Aω1)^2 \]
\[ ∆U_2=V\frac{1}{2}EK_2ε^2=m\frac{3}{2}(Aω2)^2 \]
Ha a (42) egyenletet osztjuk a (43) egyenlet azonos oldalaival akkor megkapjuk a (44) összefüggést a mérési frekvencia és a komplex modulus hányadosára.
\[ \frac{{EK}_1}{{EK}_2}=\left(\frac{\omega_1}{\omega_2}\right)^2 \]
A (27) egyenlet megadja komplex modulus változását a hőmérséklet függvényében, ezért a (27) a (44) egyenlet (27) egyenletbe helyettesítésével megkapjuk a mérési frekvencia és a hőmérséklet összefüggését, vagyis a keresett eltolási egyenletet, ahol az f terhelés frekvenciájának változása arányos kell legyen a molekula \omega rezgési frekvenciájának változásával.
A (27) egyenletben a moláris hőkapacitás szerepel, ami 1 mólnyi tömegre vonatkozik, míg a (42) egyenletben már V térfogatra vonatkozó tömeg van, ezért a fajlagos hőkapacitással számolunk.
\[ f_1=f_2\sqrt{{\ e}^{-\left[\frac{a1\left(T_2-T_1\right)^3+a2\left(T_2-T_1\right)^2+a3\left(T_2-T_1\right)}{\ T_2T_1}\right]}} \]
ahol:
\( a_1 \); \(a_2 \); \(a_3 \) – eltolási függvény paraméterei
A (45) eltolási egyenlet azt jelenti, hogy a \( T_1 \) hőmérsékleten és \( f_1 \) terhelési frekvencián ugyanakkora komplex modulust mérünk, mint \( T_2 \) hőmérsékleten és \( f_2 \)terhelési frekvencián.
A \( \rho \) sűrűségű anyag komplex modulusának \( {EK}_1 \)-ről \( {EK}_2 \)-re változtatásához \( v(T_1)=\omega(T_1)A(T_1) \) sebességről \( v(T_2)=\omega(T_2)A(T_2) \) sebességre kell növelni, ahol a paraméterek hőmérsékletfüggők.
Az amplitúdók összefüggése a (39) alapján:
\[ A(T_2)\ =A(T_1)\left[1+\int_{T_1}^{T_2}\alpha\left(T\right)dT\right] \]
Az m tömegű anyag \( T_1 \) hőmérsékletről \( T_1 \) hőmérsékletre változtatásához az (31) alapján:
\[ ∆U=\frac{3}{2} m[{ω(T_2)A(T_1)[1+\int_{T_1}^{T_2}\alpha(T)dT]}^{2}-{ω(T_1)A(T_1)}^{2}] \]
\[ ∆U=m\int_{T1}^{T2}c(T)dT \]
Az aszfaltkeverékek tájékoztató fajlagos hőkapacitása ~ 950 (J kg-1 K-1) vagy (m2 K-1 s-2).
Alkalmazás
A levezetett (45) eltolási függvényt közvetlenül alkalmazhatjuk a „hagyományos” Sigmoid függvényekhez (1) és (2). A (45) értelemszerű átalakításával jutunk a (49) \( a_T \) hagyományosan értelmezett eltolási függvényhez.
\[ a_T=\sqrt{{\ e}^{-DB}} \]
ahol:
\( B=\left[a_1\left(T_{sz}-\ T_b\right)^2+a_2\left(T_{sz}-\ T_b\right)+a_3\right] \)
\( D=\frac{\left(T_{sz}-\ T_b\right)}{T_{sz}T_b} \)
A (49) eltolási függvény alkalmazása minden esetben jobb, vagy lényegesen jobb, kisebb RMS% értéket biztosított a mért komplex modulusokkal, mit az ismert (3), (4), (5) empirikus egyenletek.
A Sigmoid közelítés nagy előnye, hogy a mért értékeket a lehető legjobban közelíti. Hátránya, hogy semmilyen fizikai törvényszerűséget nem követ, pusztán jó korrelációt biztosít az esetlegesen rossz, mérési hibákkal teli esetekben is.
A termo módszernél (27) és (45) a vizsgálati frekvenciák és mérési hőmérsékletek közül kiválasztunk egyet pl. \( f_r =10 Hz \) referencia frekvenciát és egy bázis \( T_b=21,1 oC \) hőmérsékletet, amelyhez tartozik egy mért komplex modulus, amit \( {EK}_b \) bázis modulussá teszünk.
A (27) egyenlet az előzőek szerinti értelmezésével felírva:
\[ {EK}_{sz}={EK}_b{\ e}^{-DC} \]
ahol:
\( C=\left[b_1\left(T_{sz}-\ T_b\right)^2+b_2\left(T_{sz}-\ T_b\right)+b_3\right] \)
\( b_1 \); \( b_2 \); \( b_3 \) – fajlagos hőkapacitás paraméterei
\( {EK}_b \) – bázis, \( f_r \) referencia frekvencián és \( T_b \) bázis hőmérsékleten mért komplex modulus (MPa)
Az (50) egyenlet csak azonos frekvenciájú mérések esetén alkalmazható. A (49) azonban megadja az összefüggést a hőmérséklet és frekvencia között.
A mestergörbéhez szükséges vizsgálatokat eltérő \( f_v \) vizsgálati frekvencián végezzük, ezért az (50) csak akkor alkalmazható, ha az eltérő \( f_v \) vizsgálati frekvenciákat egy közös \( f_r \) referencia frekvenciára vonatkoztatjuk, de ekkor a vizsgálati \( T_v \) vizsgálati hőmérsékletet a (49) egyenlet segítségével át kell számítani egy \( T_{sz} \) számított korrigált hőmérsékletre (51), ahol a \( T_{sz} \) fokozatos közelítéssel is számítható.
\[ \left(\frac{f_r}{f_v}\right)^2={\ e}^{-\left[\frac{a1\left(T_{sz}-T_v\right)^3+a2\left(T_{sz}-T_v\right)^2+a3\left(T_{sz}-T_v\right)}{\ T_v\ T_{sz}}\right]} \]
Az (51) egyenlet az jelenti, hogy az \( f_v \) vizsgálati frekvencián és \( T_v \) vizsgálati hőmérsékleten mért komplex modulus értéke nem változik, ha a vizsgálatot \( f_r \) referencia frekvencián és \( T_{sz} \) számított hőmérsékleten végezzük.
Az egyenleteket a jobb érthetőség miatt nem indexeltem, de ez azt jelenti az 1. táblázati adatok feldolgozása után, hogy pl. a 3. táblázat szerint 0,5 Hz-en és 54,4 oC- mért \( T_v \)vizsgálati hőmérséklete helyett a 10 Hz \( f_r \) referenciának választott frekvenciára (51) alapján átszámítva a \( T_{sz} \) hőmérséklet Thermo módszerrel 70,8 oC lesz. A 10 Hz-en és 70,8 oC-on mért komplex modulusnak egyeznie kell a 0,5 Hz-en és 54,4 oC- mért komplex modulus értékkel.
A (49), (50) és (51) egyenletekkel, amit Thermo módszernek neveztem el a hőkapacitás paramétereinek ismeretében, vagy a paramétereket iterációs módszerrel számolva a komplex modulus hőmérséklet-frekvencia függvénye számítható. A számítást mindig egy referencia \( f_r \) frekvencián pl. 10 Hz és \( T_b \) bázis hőmérsékleten 21,1 oC végezzük.
A hőkapacitás hőmérséklet szerinti határozott integráljából adódnak a hőkapacitás paraméteri. Az integrálást az 5. ábra szerint a \( T_{sz\ i} \) és a \( T_{b\ i} \) között kell elvégezni, ahol a \( ∆Hi \) entalpia változó. A hőkapacitás hőmérsékleti függvényét azonban nem ismerjük, ezért a paramétereket a komplex modulus mért értékeiből határozzuk meg. Az iteráció következtében a paraméterek értéke függ a referencia frekvencia és a bázis hőmérséklettől is, amely változás kizárólag a konstans értékeknél megengedett, de ezt az eltérést a hőkapacitás mérésével lehetne megfelelően javítani. A konstans értékek \( a_3 \) \( b_3 \) a hőmérséklet növelésével növekszenek, ami kristályosodásra utal, mivel a kristályosodás hőfelszabadulással jár. Alacsonyabb hőmérsékleten a kristályosodás valószínűsége megnövekszik, ezért a kristályosodás következtében felszabaduló hő csökkenti a hőmérséklet változásához szükséges hő mennyiségét az entalpiát a (18) egyenlet szerint.
 |
Hagyományos számítás esetén (2) Sigmoid függvény alkalmazásakor a \( T_{sz} \) minden esetben egyezik a vizsgálati hőmérsékletekkel, ekkor nincs korrekció.
A Sigmoid közelítést úgy számoltam, hogy az eltolási függvényt a (49) adja, ennek megfelelően az illesztési paraméterek:
| Sigmoid | (49) eltolás | (50) termo | |||
| a | 4,41 | a1 | 4,6 | b1 | -0,29 |
| b | 6,04 | a2 | -39,6 | b2 | 36,5 |
| c | 0,68 | a3 | 43295 | b3 | 4278 |
| d | 0,16 | ||||
A kétféle független módszer Sigmoid közelítés és a Thermo közelítés (50) azonos RMS% eredményt ad, ha a 2. táblázat szerinti közös (49) eltolási paraméterekkel számolunk. Ha megengedjük az eltérő eltolási paramétereket, akkor mindkét esetben kis mértékben csökken, javul a mért és a számított értékek négyzetes eltérése RMS, de egy aszfaltkeverék esetén csak egy „valós” eltolás lehetséges.
Az együttes hiba minimalizálása esetén RMS=4,36%, az 7. ábra szerinti eredményt kapjuk.
 |
A kétféle számítási módszert alkalmazhatjuk, az esetleges mérési hibák feltárására is.
Ha a Sigmoid módszert és a Thermo módszert egymástól függetlenül alkalmazzuk, akkor a (51) segítségével mindkét esetben számíthatjuk egy adott \( f_r \) referencia frekvenciára vonatkozó a \( T_{sz} \) számított korrigált vizsgálati hőmérsékletet. A 3. táblázatban a \( f_r \) referencia frekvencia 10 Hz, míg a \( T_b \) bázis hőmérséklet 21,1 oC. A 3. A 3. táblázatban a két módszer szerinti hőmérsékleti különbség magas hőmérsékleten és alacsony frekvencián nem elhanyagolható. Ilyen mértékű eltérés nem szükségszerű, sok vizsgálat esetén az eltérés 0,5 oC alatt marad.
A 3. táblázatban a \( T_{sz} \) számított korrigált vizsgálati hőmérsékletei azt jelenti, hogy pl. a 0,1 Hz-en és 37,8 oC-on mérés termodinamikailag egyezik a 10 Hz-en és 60,7 oC-on végzett méréssel.
| Frekvencia (Hz) referencia 10 Hz | ||||||
| 25 | 5 | 1 | 0,5 | 0,1 | ||
| Sigmoid | ||||||
| Mérési hőmérséklet (oC) | -10 | -12,5 | -8,1 | -3,4 | -1,4 | 3,5 |
| 4,4 | 1,3 | 6,8 | 12,6 | 15,2 | 21,4 | |
| 21,1 | 17,3 | 24,0 | 31,1 | 34,2 | 41,7 | |
| 37,8 | 33,6 | 41,0 | 48,8 | 52,3 | 60,7 | |
| 54,4 | 50,1 | 57,7 | 65,6 | 69,2 | 77,7 | |
| Termo | ||||||
| -10 | -10,0 | -8,3 | -4,2 | -2,4 | 1,9 | |
| 4,4 | 4,4 | 6,7 | 12,4 | 14,8 | 20,8 | |
| 21,1 | 21,1 | 23,9 | 30,7 | 33,8 | 41,1 | |
| 37,8 | 37,8 | 40,6 | 47,3 | 50,2 | 57,3 | |
| 54,4 | 54,4 | 56,8 | 62,4 | 64,9 | 70,8 | |
| Hőmérsékleti különbség > 0,5 oC | ||||||
| -10 | 0,8 | 1,0 | 1,6 | |||
| 4,4 | 0,7 | |||||
| 21,1 | -0,6 | -1,0 | ||||
| 37,8 | 0,6 | -1,6 | -2,1 | -3,4 | ||
| 54,4 | 1,1 | -0,9 | -3,0 | -4,0 | -6,6 | |
A Sigmoid és a Thermo számítás eredménye nem teljesen azonos, feltételezzük, hogy az eltérést vizsgálati „hiba”.
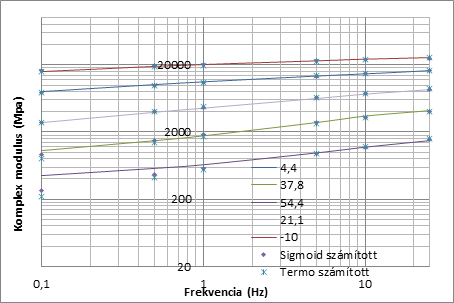 |
Lehetőségünk van a durva hibák, a 2 oC-nál nagyobb eltérések kizárására 8. ábra, és a két módszer együttes futtatására, ekkor a négyzetes eltérés a hibával nem érintett pontokon tovább javul RMS=2,85%, ami alacsony érték, viszont a hibával terhelt pontoktól már jelentős lesz az eltérés.
 |
A számításokat elvégeztem a -10 oC-os vizsgálati mérések elhagyásával 9. ábra, de számítottam a -10 oC-ra is a komplex modulusokat is. A -10 oC-on mért, de az illesztésnél figyelembe nem vett Thermo módszerrel számított RMS=7,0% lett.
A kétféle módszer együttes használata minden esetben javította a mérési határon kívüli esetre vonatkozó számítás, extrapoláció megbízhatóságát.
Végezetül a 10. ábrán bemutatom az 1. táblázat mérési eredményeit a Thermo módszerrel egységesen 10 Hz frekvenciára átszámított grafikonját, amely jól közelíthető polinommal. A polinomos közelítés már jól használható a pályaszerkezet méretezésénél és az aszfaltkeverék tervezésnél.
 |
Következtetések
A tanulmányban igazoltam, hogy a termodinamikai törvények közvetlen alkalmazásával az aszfaltkeverékek mechanikai viselkedése tulajdonsága meghatározható, nemcsak elméleti, hanem a mérnöki gyakorlat számára is közvetlenül hasznosítható formában.
- A termodinamika törvényekből közvetlenül levezetett Thermo módszerrel az eddig alkalmazott eltolási függvényeknél pontosabb számítási módszer, a mért értékekkel összevetve jobb RMS%-ot eredményez.
- Az eddig kizárólagosan alkalmazott matematikai Sigmoid függvény helyett, fizikai jelentésű a termodinamikán alapuló Thermo egyenletekkel a mérnöki gyakorlat számára.
Jelölésjegyzék:
\( a_T \) – eltolási függvény
\( f_{sz} \) – számított eltolási frekvencia (Hz)
\( f_b \) – bázis vagy mérési frekvencia (Hz)
\( EK \) – számított komplex modulus (MPa)
\( T \) – hőmérséklet (K)
\( T_r \) – referencia hőmérséklet, amely hőmérséklethez viszonyítunk (K)
\( T_b \) – bázis vagy vizsgálati hőmérséklet (K)
\( T_v \) – vizsgálati hőmérséklet (K)
\( T_{sz} \) – számított hőmérséklet (K)
\( p \) – nyomás (Pa) vagy (J/ m3)
\( V_m \) – moláris térfogat (dm3 *mol-1)
\( R \) – egyetemes gázállandó 8,315 (J *mol-1*K-1)
\( T_0 \) – abszolút nulla hőmérséklet -273,15 (oC)
\( \alpha \) – hőtágulási együttható
\( k_B \) – Boltzmann állandó 1,380649·10−23 J/K
\( N_a \) – Avogadro-konstans 6,02217046⋅1023 db/mol
\( f_i \) – azon molekulák aránya amelyeknek kinetikus energiája meghaladja a megadott \( E_i \) küszöbenergiát,
\( E_i \) – a megadott \( E_i \) küszöbenergia szint (J)
\( L_b^T \) – belső munka T hőmérsékleten (J)
\( \sigma_{x,y,z} \) – X,Y,Z irányú normál főfeszültségek (MPa)
\( \varepsilon_{x,y,z} \) – X,Y,Z irányú fajlagos alakváltozás
\( Q \) – hő (J)
\( C_{mp} \) – moláris hőkapacitás \( J\ {{mol}^{-1}K}^{-1}\ ) \), állandó nyomáson
\( C_{mV} \) – moláris hőkapacitás \( J\ {{mol}^{-1}K}^{-1}\ ) \), állandó térfogaton
\( n \) – anyagmennyiség
\( ∆H \) – entalpia (J)
\( E_a \) – aktiválási energia (J* mol-1)
\( V \) – térfogat
\( V_o \) – van der Waals térfogat, ahol már nem lehetséges a folyás
\( \eta \) – viszkozitás (Pa s)
\( K_T \) – egyensúlyi állandó T hőmérsékleten
\( k \) – reakciósebességi állandó (mol/sec)
\( A^{pre} \) – preexponenciális tényező (mol/sec)
\( E_0 \) – aktiválási energia (J/mol)
\( R \) – egyetemes gázállandó 8,315 (J *mol-1*K-1)
\( z \) – a másodpercenkénti ütközési szám (db/s)
\( f \) – sztérikus faktor \(f\le1,0\) azon ütközések aránya melyek orientációja reakcióhoz vezet.
\( v \) – sebesség (m/s)
\( U \) – belső energia (J)
\( A_{x,y,z} \) – tengelyirányú amplitúdó (m)
\( \omega_{x,y,z} \) – tengelyirányú frekvencia (1/s)
\( m \) – tömeg (g)
\( f_k \) – terhelés körfrekvenciája s-1; Hz
\( \rho \) – sűrűség kg m-3, \( \rho=\frac{m}{V} \)
\( c(T) \) – fajlagos hőkapacitás J kg-1 K-1 vagy m2 K-1 s-2)
\( A(T) \) – a molekula rezgésének átlagos amplitúdója T hőmérsékleten (m)
Paraméterek:
\( a;b \) – a Sigmoid függvény számított eltolási paraméterei (MPa)
\( c;d \) – a Sigmoid függvény számított dimenzió nélküli paraméterei
\( g;h \) – számított eltolási paraméterek (K)
\( a_h;\ b_h \) – az anyagra jellemző hőtágulási mérési állandók
\( C_1;C_2\ \)- WLF függvény eltolási paraméterei
\( a;b;c \) – Witzak-féle eltolási paraméterek
\( \alpha ;\beta;\gamma \) – illesztési paraméterek, vagy a moláris hőkapacitás paraméterei
\( a_1;a_2;a_3 \) – eltolási függvény paraméterei
\( b_1;b_2;b_3 \) – fajlagos hőkapacitás paraméterei
Irodalomjegyzék
[1]: Levenberg, E. & McDaniel, R. S. 2009. Validation of NCAT Structural Test Track Experiment Using INDOT APT Facility, Indiana: Purdue University, FHWA/IN/JTRP-2008/26.
[2]: Fakhri, M. & A. R. Ghanizadeh, 2013. Effect of Waveform, Duration and Rest Period on Resilient Modulus of Asphlat Mixis. 2nd Conferenc of Transport Research Group of India, ScienceDirect. https://doi.org/10.1016/j.sbspro.2013.11.100
[3]: Calderon, A. U. 2009. Characteristics Of Dynamic Triaxial Testing Of Asphalt Mixtures, Reno: University of Nevada.
[4]: Tóth, Cs. 2010. Aszfaltkeverékek merevsége a terhelési idő, a hőmérséklet és a kőváz szemeloszlásának függvényében. BMGE Ph.D. értekezés.
[5]: Witczak., M. V. & Mirza, M. 1995. Development of a Global Aging System for Short and Long Term Aging of Asphalt Cements. Journal of the Association of the Asphalt Paving Technologists, 64. kötet, pp. 393-430.
[6]: Williams, M. L., Landel., R. F. & Ferry, J. D. 1955. The temperature dependence of relaxation mechanisms in amorphous polymers and outher glass forming liquids. J. Am. Chem. Soc., 77. kötet, pp. 3701-3707.
[7]: Kohout, J. 2021. Modified Arrhenius Equation in Material Science, Chemistry and Biology. Molecules; https://doi.org/10.3390/molecules26237162 , 26. kötet.
[8]: Rowe, G. M. & Sharrock, M. J. 2010. Alternate Shift Factor Relationship for Describing the Temprerature Dependency of the Visco-Elastic Behaviour of Asphalt Materials. https://doi.org/10.3141/2207-16
[9]: Kaelble, D. 1985. Computer-Aided Design of Polymers and Composites. Marcel Dekker, pp. 145-147.
[10]: Witzak, M. & Bari, J. 2004. Development of a Master Curve (E*) Database for Lime Modifide Asphaltic Mixtures. Arizone State University, AZ 85287-5306. kötet.
[11]: Yousoff, N. I. M., Chailleux, E. & Airay, G. D. 2011. A CoMParative Study of the Influence of Shift Factor Equations on Master. International Journal of Pavement Research and Technology, ISSN 1997-1400. 4(6): 324-336.
[12]: Arrhenius, S. 1889. Über die Dissociationswärme und den Einfluß der Temperatur auf den Dissociationsgrad der Elektrolyte. Z. Physik. Chem., 4. kötet, pp. 226-248.
[13]: László, K., Grofcsik, A., Kállay, M. & Kubinyi, M. 2012. Fizikai Kémia I. Kémiai termodinamika. 2. javított szerk. Budapest, Tipotex Kiadó.
[14]: Bárány, S. és mtsai., 2009. Fizikai kémia műszakiaknak. Budapest: Nemzeti Tankönyvkiadó.
[15]: Kürti, M. 1992. A hőmérséklet fogalma. Fizikai Szemle, 9. kötet, p. 281.
[16]: Zhao, Y., Jiang, J., Dai, Y. & Ni, F. 2020. Thermal Property Evalution of Porous Asphalt Concrte Based on Heterogeneus Meso-Structure Finite Element Simulation. MDPI. https://doi.org/10.3390/app10051671
[17]: Mamlouk, M., Witzak, M. W., Kaloush, K. & Hasen, N. 2005. Determination of Thermal Properties of Asphalt Mixture. Journal of Testing and Evalution, 33. kötet. https://doi.org/10.1520/JTE12592
[18]: Batschinki, A. 1913. Z. physik. Chem., 84. kötet, p. 644.
[19]: Cohen, M. 1959. Molecular Transport in Liquids and glasses. The Journal of Chemical Physics, 5. kötet, p. 1164.
[20]: Messaadi, A. és mtsai. 2015. A New Equation Relating the Viscosity Arrhenius Temperature and the Activation Energy for Newtonian Classical Solvet. Journal of Chemistry, p. 12. https://doi.org/10.1155/2015/163262
[21]: Egami, T., Levashov, V., Aga, R. & Moris, J. 2007. Atomic Dinamics in Metal Liquids and Glasses. Materials Transaction, 48(7), pp. 1729-1733. https://doi.org/10.2320/matertrans.MJ200763
[22]: Zsichla, L. 2024. Az aszfaltkeverék szilárdságának jelentősége a méretezésben és mérésének lehetőségei. Az Aszfalt, 1. kötet, pp. 15-24.
[23]: Hoff, M. v. ‘. 1885. L’équilibre chimique dans les systèmes gazeux on dissous à l’état dilué. https://doi.org/10.1002/recl.18850041207 , 12. kötet, pp. 424-427.
Erre a szövegre így hivatkozhat:
Zsichla László: Az aszfaltkeverékek tulajdonságainak hőmérsékletfüggése a termodinamika törvényei alapján, 2024, DOI: 10.36246/UL.2024.2.07
