https://doi.org/10.36246/UL.2020.1.06
2020; 8. évfolyam, 13. szám
Pdf: A Ramberg-Osgood modell alkalmazása az aszfalt technológiában
Bevezetés
Közismert, hogy az aszfaltkeverékeknek a viselkedése a terhelés jellegétől és a vizsgálati hőmérséklettől alapvetően függ. Ennek köszönhetően a keverékek élettartamuk jelentős részében viszkoelasztikus anyagnak tekinthetők, azaz a viszkózus és rugalmas tulajdonságok egyidejű jelenléte kimutatható, ami jelentősen megnehezíti nem csak az aszfalt-pályaszerkezetek méretezését, de a keverékek vizsgálatát is.
A hazai gyakorlat szerint a keverékek egyik legfontosabb jellemzője a merevség, ami a komplex modulus abszolút értéke. Leggyakrabban a keverékek merevségét rögzített körülmények (pl. 15 °C-on, 10 Hz terhelés) mellett vizsgálják, mivel ez a paraméter alapvetően függ a hőmérséklettől, illetve a terhelési időtől. A rögzített hőmérsékleten meghatározott egyetlen merevségi értékkel a keverékek egymáshoz képest ugyan minősíthetők, de a keverékek közötti különbségek már nem tárhatók fel teljeskörűen. Erre ad megoldást a reológiából jól ismert hőmérséklet-idő hasonlósági elv felhasználásával létrehozott ún. mestergörbe. A mestergörbével a különböző hőmérsékleten és frekvencián mért dinamikus merevségek részletesen tanulmányozhatók, továbbá – közvetve – a plasztikus deformációs, illetve alacsony hőmérsékletű repedési hajlam is vizsgálható.
A gyakorlatban a mestergörbéket jellemzően szigmoid-függvényekkel szokás megkonstruálni, pedig erre a célra más függvénykapcsolatok is jól felhasználhatók. Az egyik ilyen lehetőség a talajok ciklikus viselkedésének modellezésére tervezett Ramberg-Osgood (RAMBO) anyagmodell. Tanulmányunkban arra teszünk kísérletet, hogy a RAMBO modell segítségével az aszfaltkeverék olyan egyedi azonosítóját teremtsük meg, amely mind az aszfaltgyártás, mind a beépítés alatt a minőségbiztosítási rendszerek egyik alapja lehet.
Elméleti háttér
A hőmérséklet-idő hasonlósági elv
Az először Boltzmann által megfogalmazott hőmérséklet-idő szuperpozíciós elv kimondja, hogy a thermoreológiai szempontból egyszerű anyagok relaxációs időállandói a hőmérsékletváltozás hatásra azonos mértékben változnak. Ebből következően a terhelési időtől függő mennyiségek, mint amilyen az aszfaltkeverékek komplex modulusa, az időtengely mentén a hőmérséklettől függő mértékben eltolható, így a különböző hőmérsékleten mért anyagi jellemzők egyetlen diagramon ábrázolhatók, amit mestergörbének nevezünk (lásd 1. ábra).
A hőmérséklet-idő szuperpozíciós alapelv tehát lehetővé teszi, hogy a különböző hőmérsékleti értékek és frekvenciák mellett begyűjtött adatokat egy referencia hőmérséklethez vagy frekvenciához viszonyítva vízszintes irányban elmozdítsuk, és ezzel a különböző izotermákat összehangolva egyetlen mestergörbét alakítsunk ki.
Az „Aszfaltkeverékek. Meleg aszfaltkeverék vizsgálati módszerei. 26. rész: Merevség. MSZ EN 12697-26:2018” című szabvány G melléklete külön kitér erre a kérdésre, miszerint: „A merevségi modulus meghatározása a kívánt terhelési időben a kívánt hőmérsékletre érvényes mestergörbe alapján lehetséges.” A szabvány nagyvonalakban ismerteti a mestergörbe meghatározás elvét és közöl egy példát, hangsúlyozva azonban, hogy a meghatározáshoz számos eljárás használható.
A szuperpozíció matematikailag az ún. redukált frekvencia bevezetésével valósítható meg. Az „ ” eltolási tényező határozza meg a vízszintes tengely mentén kívánt elmozdulást az adott hőmérsékleten. A tényleges „ ” frekvenciát ezzel az eltolási tényezővel kell szorozni, hogy megkapjuk a mestergörbe redukált frekvencia értékét:
\[f_{r}=a_{T}\cdot f\]
A referencia hőmérsékleten az eltolási tényező természetesen: \( a_{T}=1 \)
 |
Az eltolási tényező meghatározása
Az MSZ EN 12697-26 szabvány általánosságban ismerteti a mestergörbe meghatározásának elvét. Ennek értelmében adott hőmérsékleten mestergörbét úgy kell létrehozni, hogy más hőmérsékleteken felrajzolt izotermákat – szigorúan csak a terhelési időtartam / frekvencia tengelyével párhuzamosan – eltoljuk. A szabvány a példában az eltolási tényező értékének meghatározásához az ún. Arrhenius-féle egyenletet alkalmazza, kiemelve, hogy más összefüggések is használhatók és példaként említi a Christensen-Anderson modellt. Az Arrhenius-féle eltolási tényező összefüggése (Md. Yusoff, Chailleux & Airey 2011):
\[\log (a_{T}) = \frac{0,4347\cdot ΔE_{a}}{\frac{R}{C_{A}}}(\frac{1}{T}-\frac{1}{T_{0}})=C_{A}\cdot(\frac{1}{T}-\frac{1}{T_{0}}) \]
ahol
| \(a_{T}\) | = | eltolási tényező |
| \(T\) | = | kísérleti hőmérséklet (K) |
| \(T_{0}\) | = | referencia hőmérséklet (K) |
| \(ΔE_{a}\) | = | aktiválási energia (J mol-1) |
| \(R\) | = | egyetemes gázállandó (8,314 J mol-1 K-1) |
| \(C_{A}\) | = | konstans (K) |
A reológiában az Arrhenius-féle egyenlet mellett a másik, a közelmúltig leggyakrabban alkalmazott összefüggés az eltolási tényező meghatározására az Williams-Landel-Ferry (WLF) egyenlet volt. Mindkét klasszikus eltolási tényező használatos bitumenek és aszfaltkeverékek vizsgálatára, de elsősorban polimerekre lettek kidolgozva, ezért alkalmazásuk napjainkban folyamatosan háttérbe szorult (Kim, Mohammad & Elseifi 2015). Az elmúlt években az aszfalttechnológia fejlődése következtében több, aszfaltkeverékre kidolgozott modell is napvilágot látott. Egy nagyszabású amerikai program (National Cooperative Highway Research Program: Guide for Mechanistic-Empirical Design of New and Rehabilitated Pavement Structures. NCHRP 1-37-A, 2004.) eredményeként megszületett eltolási tényező értéke például a kötőanyag hőmérsékletfüggő viszkozitás értékeitől függ, de számos egyéb összefüggés is kidolgozásra került.
Nagyszámú rendelkezésre álló mérési eredmény esetén azonban lehetséges a klasszikus eltolási tényezők helyett az adatokra legjobban illeszkedő összefüggés paramétereinek valamilyen iterációs technika segítségével történő meghatározásakor az eltolási tényezőt is független változóként kezelni. Az optimálás elvégzésekor az eltolási tényezőt a nemzetközi szakirodalom jellemzően másodfokú függvénnyel javasolja megadni, például:
\[\log (a_{T})=a\cdot(T-T_{0})^2 + b\cdot(T-T_{0}) \]
| \(a_{T}\) | = | eltolási tényező |
| \(T\) | = | kísérleti hőmérséklet |
| \(T_{0}\) | = | referencia hőmérséklet |
| a, b | = | együtthatók |
Az eltolási tényezőkről további részletes ismertetőt ad Rowe és Sharrock (2011) kiváló munkája.
 |
Mestergörbe meghatározás szigmoid modellel
Amerikai kutatások (NCHRP 1-37-A 2004) fényében aszfaltkeverék esetén a mestergörbe egy folytonos, nem csökkenő, és szükségképpen alul – felül korlátos függvény, ennek figyelembevételével így egy nemlineáris S-alakú, ún. szigmoid függvénnyel leírható. A függvény alkalmazhatósága egyébként a keverék viselkedésének fizikai megfigyelésével is igazolható. Általános képlete az alábbi:
\[ f(x) = \frac{1}{1+e^{-a\cdot x}} \]
A mérési eredmények, merevségek birtokában megszerkeszthető a keverék mestergörbéje, amely aszfaltkeverékek esetén az alábbi képlettel írható le a frekvencia függvényében (Tóth, 2010):
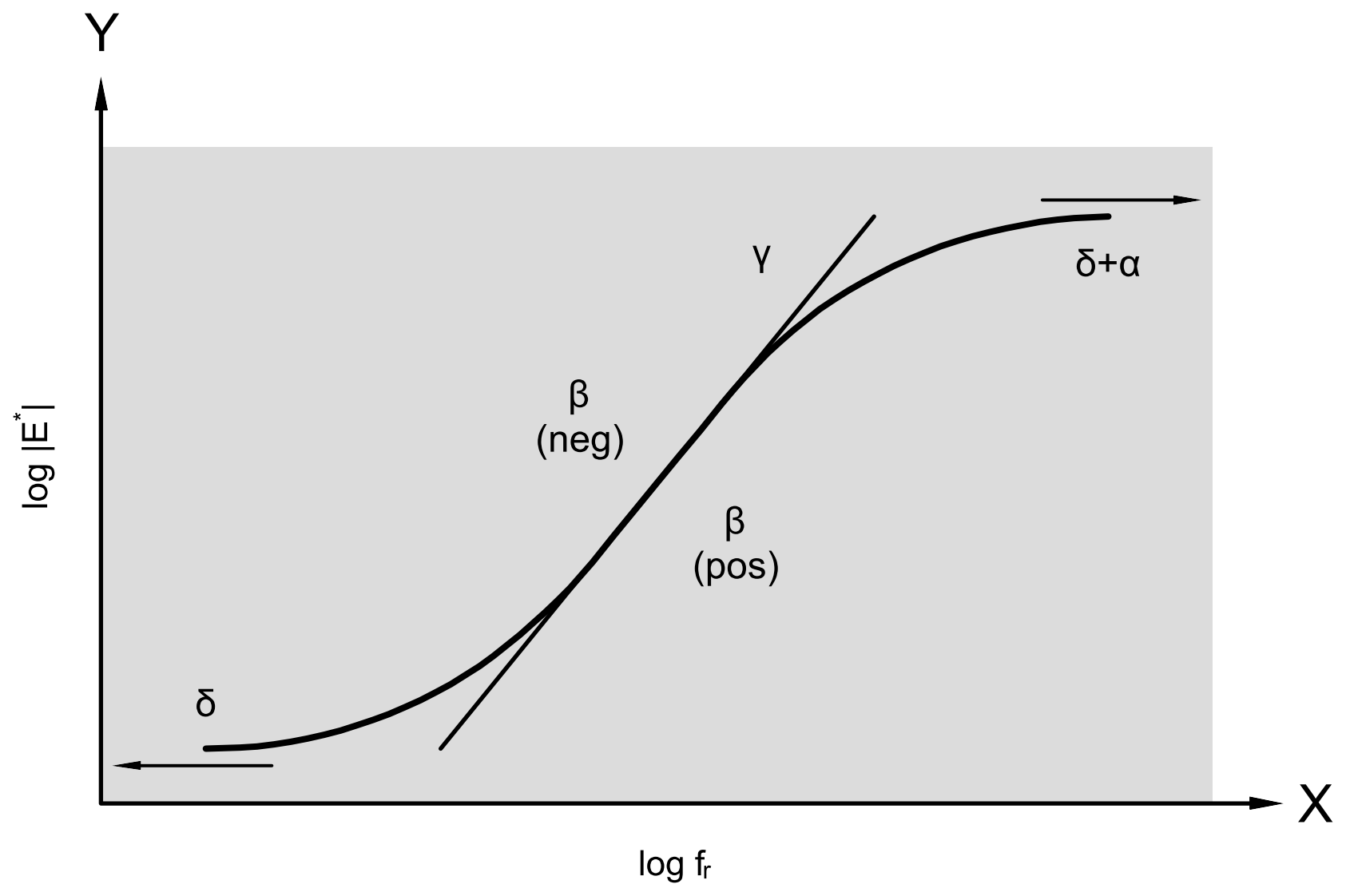
\[ \log |E^{*}|=δ+\frac{α}{1+e^{β+γ\cdot \log (f_{r})}} \]
| \(|E^{*}|\) | = | merevség (MPa) |
| α, β, γ, δ | = | regressziós paraméterek |
| \(f_{r}\) | = | redukált frekvencia (Hz) |
Az (5) sz. egyenletekben, δ az |E*| merevség minimumértéke, a δ+α az |E*| merevség maximum értéke, β és γ pedig a szigmoid-függvény paraméterei. A 2. ábra a szigmoid modell paramétereinek grafikus értelmezését mutatja. A modell nagy hátránya, hogy a keverék komplex modulusa helyett annak csupán abszolút értékét, a merevséget használja, így például a fázisszög segítségével megfigyelhető viszkoelasztikus hatás a keverék viselkedésben nem tanulmányozható.
A Ramberg-Osgood (RAMBO) modell
A mestergörbéket elsődlegesen a szigmoid-függvények felhasználásával szokás megkonstruálni, noha erre a célra más típusú függvények is felhasználhatók lennének. Az egyik ilyen lehetőség a talajok ciklikus viselkedésének modellezésére tervezett Ramberg-Osgood anyagmodell (Szilvágyi & Ray 2018). A Ramberg-Osgood függvény általános matematikai alakja:
\[ x=y+C \cdot y^{R} \]
Kweon (2008) az aszfaltkeverékek mestergörbéjének leírására az alábbi formában javasolja a fenti függvényt felhasználni:
\[f_{r}=E_{n} \cdot f_{r} + C \cdot (E_{n} \cdot f_{r})^{R} \]
ahol \(f_{r}\) a redukált frekvencia, \(E_{n}=(|E^{*}|-|E^{*}|_{min})/(|E^{*}|_{max}-|E^{*}|_{min}) \) normalizált dinamikus merevség, C és R pedig modellállandók.
A Ramberg-Osgood modellt – a szigmoid-függvényekhez hasonlóan – optimalizációs eljárások segítségével lehetséges illeszteni a mérési eredményekre. Az illesztés eredménye az \(|E^{*}|_{min} \), \(|E^{*}|_{max} \) , C és R paraméterek.
Kweon (2008) munkájában kimutatta, hogy a RAMBO modell paraméterei egymástól független hatást fejtenek ki a mestergörbére (lásd 1. táblázat).
| Paraméter | Mestergörbe | ||||
| Abszolút érték | Alak | ||||
| Min. | Max. | Görbület | Eltolás | ||
| Szigmoid-függvény | δ | ○ | ○ | x | x |
| α | x | ○ | x | ○ | |
| β | x | x | ○ | x | |
| γ | x | x | x | ○ | |
| Ramberg-Osgood modell | \(|E^{*}|_{min}\) | ○ | x | x | x |
| \(|E^{*}|_{max}\) | x | ○ | x | x | |
| R | x | x | ○ | x | |
| C | x | x | x | ○ | |
○: befolyásolja, x: nem befolyásolja
Az R a mestergörbe görbületét (dőlését) befolyásolja, a pedig – a hőmérséklet-idő eltolási tényezőhöz hasonlóan – a vízszintes tengelyen mozgatja azt. Ez utóbbi megállapítást nem vizsgálja részletesebben a szerző. A RAMBO modell együtthatóinak függetlensége lehetővé teszi a mestergörbe teljes morfológiájának numerikus jellemzését, ami az egyes keverékfajták gyors összehasonlításának lehetőségét rejti magában.
Anyag és módszer
A BME Út és Vasútépítési Tanszékén egy 2015-ös kutatásban a gumival modifikált aszfalkeveréket egy polimerrel modifikált és egy konvencionális kötőanyagú referencia keverékekkel hasonlítottuk össze (Kisgyörgy, Tóth & Geiger 2016). A vizsgálatba bevont három azonos kővázú aszfaltkeverék:
- AC22 kötő 50/70, mint referencia keverék
- AC22 kötő PmB 25/55-65, mint referencia keverék
- AC22 kötő GmB 45/80-55, mint fő vizsgálati keverék
A kutatásban arra kerestük a választ, hogy a keverékek merevségei alapján készített mestergörbék segítségével milyen további információk nyerhetők a gumival modifikált aszfalkeverékről. A három keverék komplex modulusát és fázis szögét SPT (Simple Performance Tester) segítségével határoztuk meg.
A vizsgálat közben mind a három keverékre, három hőmérsékleten, hat különböző frekvencián rögzítettük a merevség értékeket az alábbi kísérleti beállítások mellett:
- Hőmérsékletek (T): 10°C, 20°C, 30°C,
- Frekvenciák (f): 0,1 Hz, 0,5 Hz, 1 Hz, 5 Hz, 10 Hz, 25 Hz.
Jelen munka során az így rendelkezésre álló komplex modulus adatokból meghatároztuk a keverékek jellemző mestergörbéjét a szigmoid és a Ramberg-Osgood modellek felhasználásával.
Az (5) szigmoid-függvényt a kísérleti és a modell által becsült merevségek négyzetes hibájának minimalizálásával (sum of square error, SSE) határoztuk meg (Md. Yusoff, Chailleux & Airey 2011):
\[SSE =∑\frac{(\log |E^{*}_{exp}(f, T)|-\log |E^{*}_{pre}(a_{T}(T, T_{ref})\cdot f, T_{ref})|)^{2}}{(log|E^{*}_{exp}(f, T)|)^2} \]
Az optimálás elvégzésekor az eltolási tényezőt a (2) Arrhenius-féle egyenlettel számítottuk 20°C referencia hőmérséklet mellett.
A szigmoid-függvény illesztésénél kapott redukált frekvenciák alapján a (7) RAMBO modell együtthatói (|E*|min, |E*|max, C és R) a kísérleti és a modell által becsült merevségek négyzetes hibájának minimalizálásával ugyancsak ismertnek tekinthetők.
A szigmoid-függvény és a Ramberg-Osgood (RAMBO) modell illeszkedését egyaránt befolyásolja a redukált frekvencia (fr = aT · f) számításánál használt aT eltolási tényező (shift faktor), ami tulajdonképpen csak a terhelési idő tengelyével párhuzamosan tolja el az adatokat. Ez a hatás a RAMBO modellnél a C paraméter megfelelő értékének felvételével is elérhető. Az eltolódás nagysága a hőmérsékletnek függvénye, így az eredeti RAMBO modellt az alábbi formára hozhatjuk:
\[f = E_{n} \cdot f + C_{T} \cdot (E_{n} \cdot f)^{R} \]
ahol f a kísérleti frekvencia, T a kísérleti hőmérséklet, \(C_{T}\) az ismeretlen időtényező és a mestergörbe dőlése. Az ismeretlen \(C_{T} = C(T)\) függvénykapcsolat minden hőmérséklet és frekvencia szinten mért kísérleti adatsor birtokában meghatározható lenne. Mivel ez sokszor fizikailag is kivitelezhetetlen, ezért csak valamilyen eltolási tényező összefüggéssel lehet minden hőmérsékletre és frekvenciára kiszámolni a dinamikus merevségeket a kísérleti beállítások alapján. A szigmoid-függvénnyel elvégezhető egy önkényesen felvett hőmérséklet tartományra a laboratóriumi adatok transzformációja, és az így nyert mesterséges \(f – |E^{*}| \) adatsorra már illeszthető a RAMBO modell.
A feltételezésnek megfelelően azt várjuk, hogy a paraméter értékén kívül más nem változik. A GmB keverék esetén az előbbiekben ismertetett elemzés eredményeit a 2. táblázat mutatja be.
| T [°C] | C | R | Emin [MPa] | Emax [MPa] |
| 0 | 0,8282 | 0,73956 | 996 | 44060 |
| 10 | 1,9129 | 0,74074 | 1000 | 45000 |
| 15 | 2,7992 | 0,74216 | 962 | 45056 |
| 20 | 4,0407 | 0,74216 | 962 | 45056 |
| 25 | 5,7613 | 0,74215 | 962 | 45056 |
| 30 | 8,1345 | 0,74008 | 1032 | 43065 |
| ÁTLAG | 0,741142 | 985 | 44549 | |
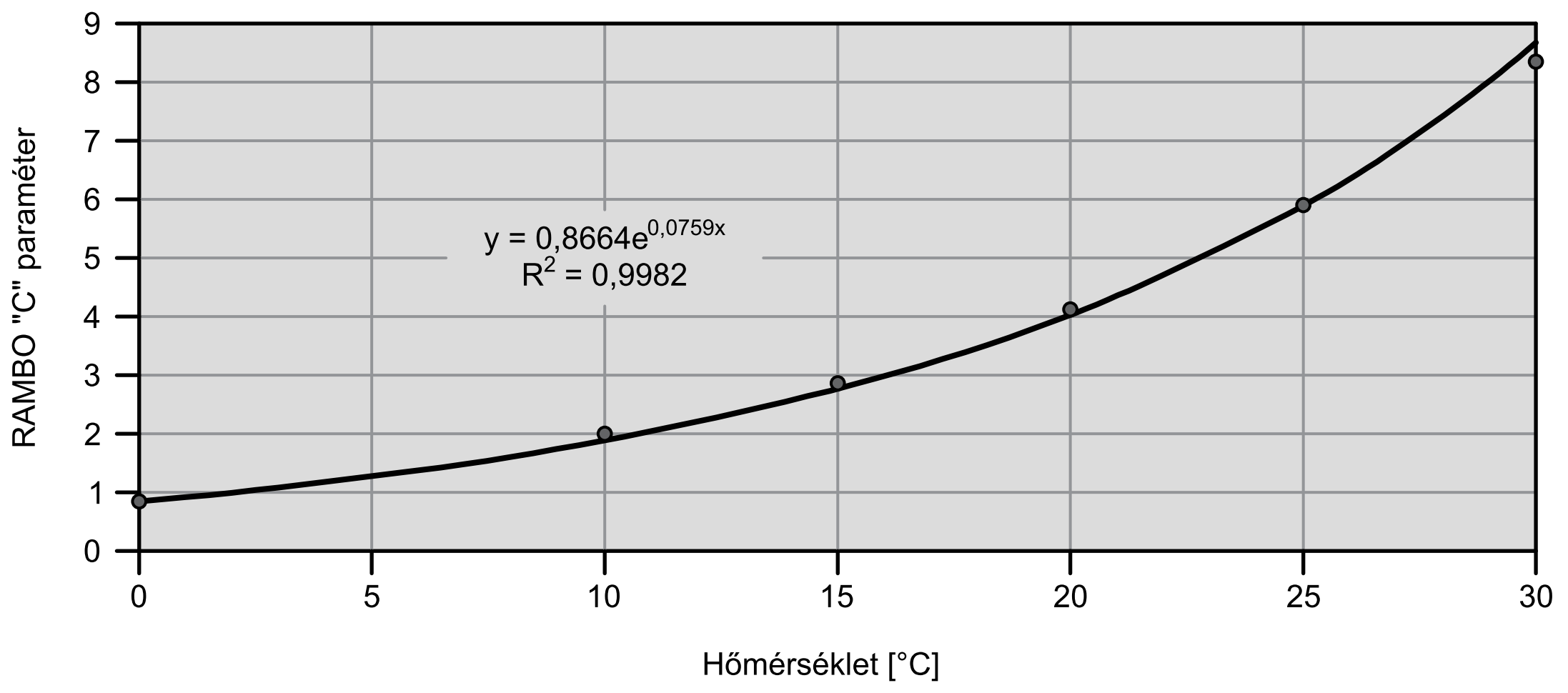
Jól látható, hogy csak a C paraméter értéke változott, a többi együttható tulajdonképpen változatlan maradt. A hőmérséklet függvényében ábrázolva a paramétert megkapjuk a keresett függvénykapcsolatot (3. ábra):
\[ C_{T}=k_{1}e^{k_{2} \cdot T} \]
 |
A (9) modell előnye, hogy az aszfaltkeverék merevségének becslésére a különböző hőmérsékleten és frekvencián végrehajtott kísérleti eredményeket egyidejűleg használja fel az ún. időtényező (\C_{T}\) segítségével, és így az (\a_{T}\) eltolási tényező elhagyható. A keresett együtthatók a kísérleti és a modell által becsült frekvenciák négyzetes hibájának minimalizálásával nyerhetők:
\[ SSE = ∑\frac{(f_{exp}-f_{pre})^{2}}{(f_{exp})^{2}} \]
ahol \(f_{exp}\) a kísérletnél beállított frekvencia és \(f_{pre}\) a RAMBO modell által becsült frekvencia a következő összefüggés alapján:
\[ f_{pre} =[\frac{k_{1}e^{k_{2}\cdot T}\cdot E^{R}_{n}}{1-E_{n}}]^{\frac{1}{1-R}} \]
A felparaméterezett RAMBO modell lehetővé teszi az eltolási tényezőt adott \(T_{ref}\) hőmérsékletre kiszámítani:
\[ a_{T} =\frac{1}{f}[\frac{k_{1}e^{k_{2}\cdot T_{ref}}\cdot E^{R}_{n}}{1-E_{n}}]^{\frac{1}{1-R}} \]
A szigmoid-függvény és a RAMBO modell illeszkedésének jóságát (R2) a becsült merevségek vagy frekvenciák segítségével egyaránt számíthatjuk. A gyakorlatban az utóbbi terjedt el, pedig a frekvenciák jóval érzékenyebben reagálnak a modell hibáira.
Eredmények és értékelés
A kutatásban vizsgált háromféle keveréktípusból két sorozat készült és mind a 6 db adatsorra illesztettük a szigmoid-függvényt és az általunk módosított RAMBO modellt. Az aszfaltbeton keverékek eredményeit a 3. és 4. táblázatok foglalják össze.
| Keverék fajta | Kód | Emin | Emax | R | k1 | k2 | R2 [f] | R2 [E*] | Tref |
| AC22 kötő
50/70 |
AG1 | 1313 | 40715 | 0,6584 | 0,1331 | 0,1142 | 0,6471 | 0,9819 | 17,7 |
| AG2 | 1515 | 32673 | 0,6351 | 0,1304 | 0,0985 | 0,7562 | 0,9878 | 20,7 | |
| AC22 kötő PmB 25/55-65 | BG1 | 2072 | 29484 | 0,6266 | 0,0902 | 0,1124 | 0,9943 | 0,9974 | 21,4 |
| BG2 | 1750 | 34667 | 0,6661 | 0,1538 | 0,0997 | 0,8052 | 0,9945 | 18,8 | |
| AC22 kötő GmB 45/80-55 | CG1 | 1686 | 25336 | 0,6351 | 0,3069 | 0,0958 | 0,9734 | 0,9976 | 12,3 |
| CG2 | 1638 | 29981 | 0,6669 | 0,4304 | 0,0894 | 0,9748 | 0,9969 | 9,43 |
| Keverék fajta | Kód | Emin | Emax | CA | γ | β | α | δ | R2 |
| AC22 kötő
50/70 |
AG1 | 987 | 34664 | 12635 | 0,87 | -1,14 | 1,55 | 2,99 | 0,9856 |
| AG2 | 1337 | 28774 | 10416 | 1,02 | -1,35 | 1,33 | 3,13 | 0,9909 | |
| AC22 kötő PmB 25/55-65 | BG1 | 1628 | 28363 | 11162 | 0,99 | -1,20 | 1,24 | 3,21 | 0,9978 |
| BG2 | 1263 | 32029 | 11221 | 0,84 | -1,12 | 1,40 | 3,10 | 0,9956 | |
| AC22 kötő GmB 45/80-55 | CG1 | 1467 | 24353 | 9985 | 0,97 | -0,13 | 1,22 | 3,17 | 0,9983 |
| CG2 | 1431 | 28363 | 10142 | 0,86 | -0,03 | 1,30 | 3,16 | 0,9977 |
A RAMBO modell pontosságát jól mutatja a becsült és beállított frekvenciák alapján számított R2, ahol az értéke kisebb mint 0,9 ott az adatsorban kiugró értékek szerepelnek, ami valószínűleg mérési hiba.
A hagyományos mestergörbe meghatározás egyik alapfeltevése, hogy egy kijelölt referencia hőmérsékleten mért merevségeket „rögzítjük” az eltolási tényezőt egynek véve, és ehhez képest mozdítjuk el a különböző hőmérsékleten mért merevségeket. A RAMBO modell alkalmazásakor ezt a megkötést nem tettük meg, így a modell illesztésekor a különböző keverékek esetén különböző hőmérsékleten kaptuk meg a legjobb illeszkedést. Alkalmazva, hogy a \(c_{T}\) időtényező az aszfaltbeton keverékre jellemző „referencia hőmérsékleten” egyenlő eggyel, visszaszámolhatóvá válik egy ún. új referenciahőmérsékletet a következő összefüggés szerint:
\[ T_{ref} = -\ln (k_{1}) \cdot k_{2}^{-1} \]
A \( T_{ref} \) hőmérsékleteket ugyancsak a 3. táblázat tartalmazza az egyes keverékekre. Ennek jelentősége, illetve elméleti értelmezhetősége még további kutatást igényel, azonban az első eredmények szignifikáns, anyagspecifikus viselkedést sejtetnek. A gumival modifikált keverékeknél a \( T_{ref} \) érték 9-12°C míg a hagyományos és polimerrel modifikált keverékeknél ez 19-22°C. Az alacsonyabb \( T_{ref} \) érték jobb hidegviselkedést enged feltételezni.
A RAMBO modellel kapott mestergörbéket a szigmoid-függvénnyel készült görbékkel is összevetettük. A szigmoid modell illesztése nyomán, az Arrhenius-féle eltolási tényezőt alkalmazva és annak \( C_{A} \) paraméterét az optimalizáció alatt változóként kezelve a 4. táblázatban szereplő értékeket kaptuk.
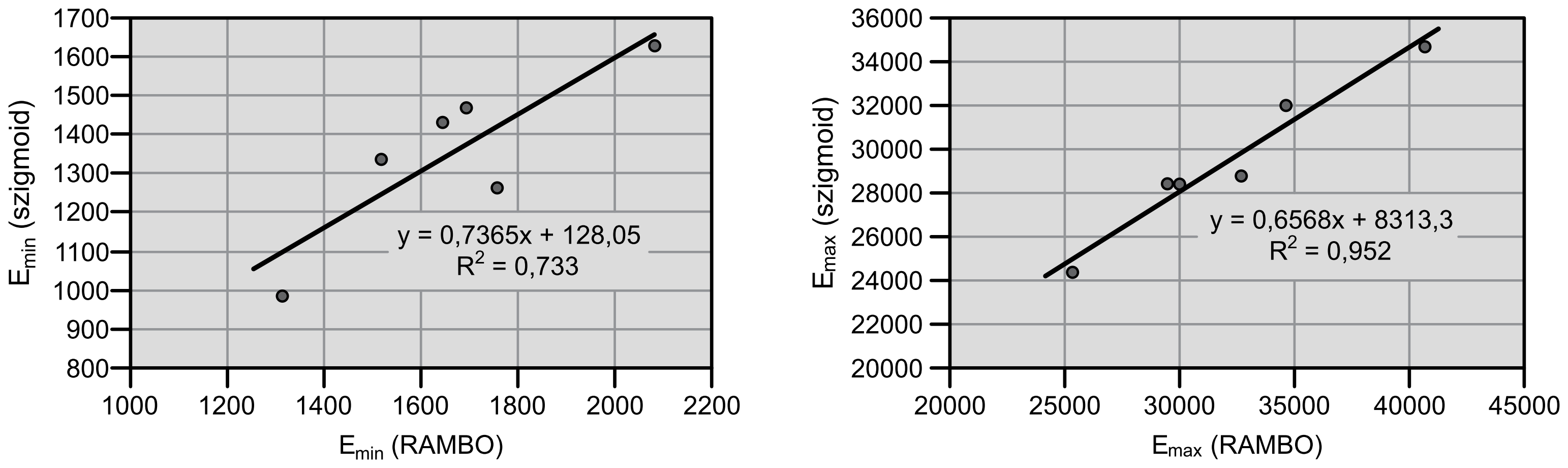
A RAMBO modell eredményeit a hagyományos szigmoid modellel grafikusan összevetve, a 4. ábrán az elméleti minimum, illetve maximum merevségek láthatók. A korreláció szorossága különböző, ugyanakkor a kapcsolat megléte igazolt.
 |
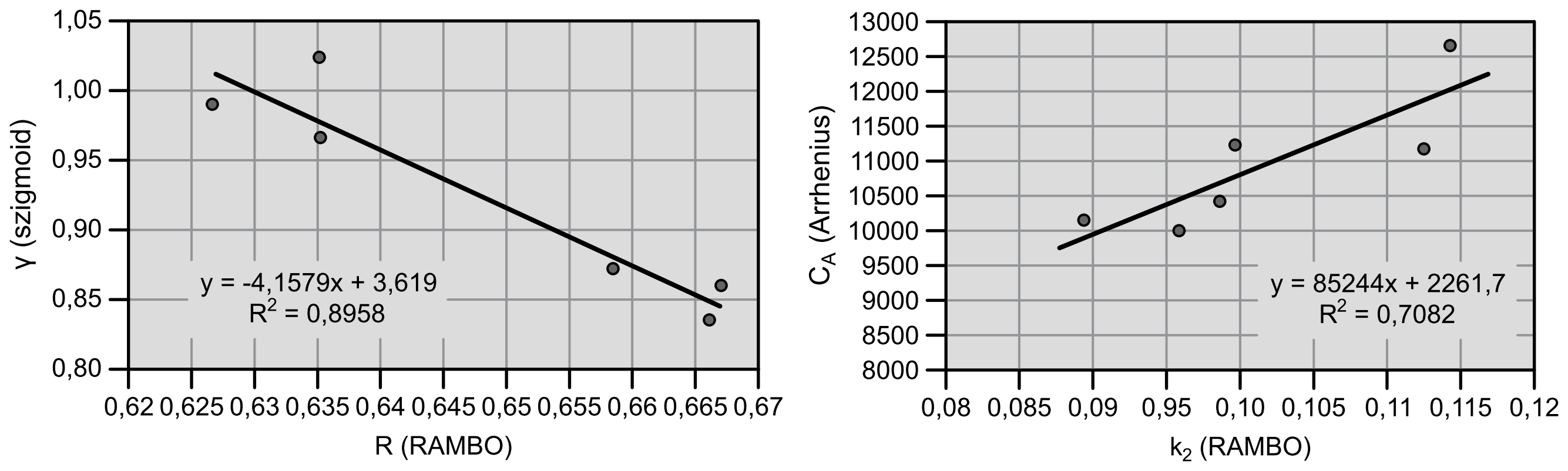 |
Az 5. ábrán a hasonló jellegű paraméterek viszonya látszik. A mestergörbe meredekségével kapcsolatba hozható γ illetve R értékek között szintén szoros a kapcsolat. Az Arrhenius-féle eltolási tényező anyagspecifikus \( C_{A} \) paramétere és az RAMBO időtényező \( k_{2} \) paramétere között szintén igazolható szignifikáns korreláció. Vizsgálatainkkal igazoltuk, hogy a két modell segítségével kapott mestergörbék nagyon hasonló jelleget mutatnak.
Összefoglalás és következtetések
Mint arra már korábban többször is utaltunk, az előírt hőmérsékleten meghatározott egyetlen merevségi értékkel ugyan a keverékek jellemezhetők, de keverékek közötti különbségek már nem tárhatók fel teljeskörűen. Egy tekintélyes munkacsoport (CROW-report 2006) az új holland aszfalt pályaszerkezet méretezési rendszer számára tett ajánlásaiban kihangsúlyozta, hogy minden esetben javasolt a mestergörbe meghatározást előírni, tekintettel annak értékes információtartalmára.
Figyelembe véve, hogy a hőmérséklet-idő ekvivalencia megteremti annak a lehetőségét, hogy olyan idő, illetve frekvencia tartományokat is tanulmányozunk, amelyek kísérletileg nem, vagy csak nagyon nehezen állíthatók be, az ehhez szükséges matematikai eszközök fejlesztése, illetve finomítása fontos feladat. Segítségükkel az aszfaltkeverékek mestergörbéjének meghatározása lehetővé teszi az összehasonlítást a különböző frekvencián és hőmérsékleten végzett vizsgálatok között, továbbá az aszfaltkeveréknek a merevség vizsgálatok során a teljes hőmérsékleti skálán megfigyelt fizikai viselkedése is rögzíthetővé válik.
Jelen tanulmányban bemutattuk az aszfaltkeverék mestergörbe meghatározásának egy lehetséges módszerét, a szigmoid-függvény mellett az ún. RAMBO modellt. A RAMBO modell vizsgálataink alapján jól képes helyettesíteni a szigmoid-függvényt a merevségadatok leírásában, együtthatóinak függetlensége pedig lehetővé teszi a mestergörbe teljes morfológiájának numerikus jellemzését, ami mind az aszfaltgyártás, mind a beépítés alatt a minőségbiztosítási rendszerek egyik alapja lehet.
Irodalomjegyzék
MSZ EN 12697-26:2018: „Aszfaltkeverékek. Meleg aszfaltkeverék vizsgálati módszerei. 26. rész: Merevség.”
National Cooperative Highway Research Program, 2004: Guide for Mechanistic-Empirical Design of New and Rehabilitated Pavement Structures. NCHRP 1-37-A
Tóth, C. 2010: Aszfaltkeverékek mestergörbéjének meghatározása; Közlekedésépítési Szemle, Vol. 60. No. 2. pp. 14–19.
Kim, M., Mohammad, L. N. & Elseifi, M. A. 2015: Effects of Various Extrapolation Techniques for Abbreviated Dynamic Modulus Test Data on the MEPDG Rutting Predictions. Journal of Marine Science and Technology 23 (3): 353–63, https://doi.org/10/gfxr36
Kisgyörgy, L., Tóth, C. & Geiger, A. 2016: Elastic modulus of asphalt with chemically stabilized rubber bitumen. Građevinar 68 (07.): 533–41, https://doi.org/10/gfx3zw
Kweon, G.C. 2008: Application of Modified Ramberg-Osgood Model for Master Curve of Asphalt Concrete. International Journal of Highway Engineering 10 (4): 31–40.
Md. Yusoff, N. I., Chailleux, E. & Airey, G. 2011: A comparative study of the influence of shift factor equations on master curve construction. International Journal of Pavement Research and Technology 4 (6): 324–36.
Rowe, G. M. & Sharrock, M. J. 2011: Alternate Shift Factor Relationship for Describing Temperature Dependency of Viscoelastic Behavior of Asphalt Materials. Transportation Research Record: Journal of the Transportation Research Board 2207 (1): 125–35, https://doi.org/10/b7wq7q
Szilvágyi, Z. & Ray, R. P. 2018: Verification of the Ramberg-Osgood Material Model in Midas GTS NX with the Modeling of Torsional Simple Shear Tests. Periodica Polytechnica Civil Engineering, február, https://doi.org/10/ggfz62
Erre a szövegre így hivatkozhat:
Tóth Csaba, Cho Seoyoung, Primusz Péter: A Ramberg-Osgood modell alkalmazása az aszfalt technológiában, Útügyi Lapok, 2020, DOI: 10.36246/UL.2020.1.06
