Bevezetés
A méretezés feladata a szerkezetek felépítésének, méreteinek és anyagainak meghatározása annak érdekében, hogy az üzemeltetés, illetve a használat közben fellépő terhelések ne okozzanak a tervezési élettartam alatt tönkremenetelt. Kezdetben a méretezés során az építőmérnöki szerkezetek geometriai méreteinek megfelelőségét túlnyomórészt építési tapasztalatokra támaszkodva ellenőrizték, legfeljebb kezdetleges számításokat végeztek. A tudományágak fejlődésével ezt a megközelítést, fokozatosan, analitikus elvű módszerek váltották fel, amelyek során a szerkezeteket érő terheket és a teherbíró képességüket egyre finomabb módszerekkel számították majd hasonlították össze. A vizsgálati és modellezési ismeretek bővülése és a matematikai valószínűség-elmélet fejlődése az 1900-as években több valószínűségi, fél-valószínűségi méretezési elmélet kidolgozásához vezetett, melyek elvét az 1. ábra szemlélteti. Ezen módszerek azon lényegi felismerésen alapultak, miszerint – Kármán megfogalmazásában – a szerkezetek méretezése során nem az abszolút, csupán az elegendő biztonság megteremtése lehet a cél (Idézi: Farkas, et al., 2015). Ezen újszerű elméletek hosszas viták, kezdeti elutasítottság után a szerkezetek és anyagok, illetve a szerkezetekhez társított elvárásokból fakadó kompromisszumok jobb kihasználását tették lehetővé.
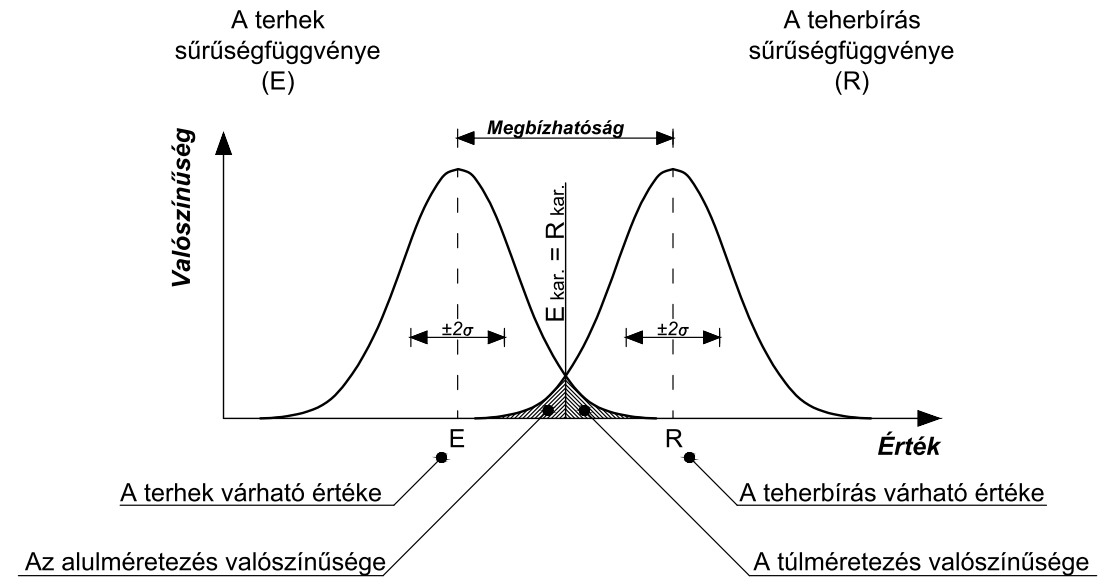 |
Az 1. ábrán bemutatott méretezési elv alapján értelmezhetővé válik a kockázat – vagy biztonság – azon elfogadható – vagy elvárt – szintje, mely az adott szerkezetnek tulajdonított szerep függvényében minden szerkezet méretezésének alapját képezi. A méretezés lényege tehát a szerkezetet érő terhek és a szerkezet terheknek való ellenálló képességének – teherbírásának – összevetése maradt, e két mennyiség megfogalmazása azonban változott, általában valószínűségi változókként kerülnek figyelembe vételre, tehát figyelembe vételre kerül az, hogy a terhek és a teherbírás értékei különböző gyakorisággal fordulnak elő (Deák, et al., 2006). A konkrét számítások során az egyes jellemzők a sűrűségfüggvényük jellegzetes pontjai szerinti karakterisztikus értékükkel kerülnek figyelembe vételre, melyek meghatározásához biztonsági tényezők kerülnek alkalmazásra (Ádány, et al., 2007).
Habár az útpályaszerkezetek is teherhordó szerkezetek, méretezési eljárásaik a klasszikus teherhordó szerkezetektől lényegesen eltérnek, tekintve, hogy a teherbíró képesség és a terhek meghatározása területén egyaránt jelentős a bizonytalanság, és a kettő pontossága között nagyságrendi különbségek is lehetnek (Karoliny, 2005). A valóságban több rétegből álló útpályaszerkezet modelljének felépítése során és az aszfaltkeverékek anyagi tulajdonságainak figyelembe vételekor ugyanis éppúgy jelentős egyszerűsítésekkel kell élni, mint a forgalomból adódó terhelések meghatározásakor, a nehézgépjármű-forgalom jellemzőiben megfigyelhető igen nagy változékonyság figyelembe vételekor. A teherbírás meghatározása azonban rendszerint sokkal pontosabban elvégezhető, mint a terhek megállapítása: az útpályaszerkezet egyes pontjaiban keletkező feszültségek és alakváltozások az 1970-es évek óta számítógéppel is modellezhetőek. A számítógépes modellezésben rejlő lehetőségek hazánkban például a típus-útpályaszerkezetek kialakításánál kerültek kihasználásra. A szerkezet igénybevételeinek meghatározásakor ezzel szemben a klimatikus és forgalmi eredetű terhekben lévő területi és időbeli változékonyság kezelhetősége érdekében továbbra is jelentős egyszerűsítések, általánosítások szükségesek, melyeket minél gyakrabban felül kell vizsgálni.
Mivel az útpályaszerkezetek és megerősítésük méretezése során a forgalomból eredő igénybevétel az egyetlen közvetlenül figyelembe vett teher, meghatározásának minél pontosabbá tétele beláthatóan igen lényeges a méretezés szempontjából. Korábbi kutatásaim során elvégeztem a tervezési forgalom meghatározási módjának érzékenységvizsgálatát, mely során az egyes input adatokat azok valóságban előforduló változékonyságával vettem figyelembe (Soós, 2016). Ezután a tervezési forgalom változékonysága szempontjából a legnagyobb hatással bíró forgalomfejlődési szorzó meghatározási módját és értékeit vizsgáltam (Soós, m.a.). Az érzékenységvizsgálat alapján felállított sorrendben a forgalomfejlődési szorzót az egyes járműosztályok járműátszámítási szorzói követték, amelyeknek dinamikus tengelysúlymérési adatok alapján való meghatározására módszertant dolgoztam ki (Soós, et al., m.a.). Jelen cikk a tervezési forgalom fontosságát, meghatározásának módját és input adatait tárgyaló kutatásom során készített negyedik cikk, amelyben megemlítem a korábbi elemzések fontosabb következtetéseit, és azokat új kutatási eredményeimmel kiegészítve foglalom össze.
A tervezési forgalom meghatározásának módszere
Az útpályaszerkezet méretezése az útkategóriától függő tervezési élettartam alatt áthaladó nehéztengelyek okozta fáradási igénybevételeken alapul, melynek meghatározását az e-ÚT 06.03.13 „Aszfaltburkolatú útpályaszerkezetek megerősítése és méretezése” c. Útügyi Műszaki Előírás (ÚME), összevont járműosztályok alapján az (1) egyenlet szerint írja elő.
\[{TF}=z\dot{}1,25\dot{}365\dot{}t\dot{}r\dot{}s\dot{}f_N\dot{}(ANF_{a}\dot{}e_{a}+ANF_{n}\dot{}e_n+ANF_{p}\dot{}e_{p}+ANF_{ny}\dot{}e_{ny})\)\((1)\]
| ahol: | |
| \(TF\) | a tervezési forgalom, [egységtengely áthaladás, darab], |
| \(z\) | az egyes 115 kN, a kettős 180 kN és az útkímélő 190 kN tengely többlet fárasztó hatását figyelembe vevő szorzó (pontosítása kidolgozás alatt), |
| \(1,25\) | a biztonsági tényező, |
| \(r\) | a keresztmetszeti forgalom irányonkénti számítására használt irányszorzó, |
| \(s\) | a sávszorzó az egy irányban vezető forgalmi sávok száma szerint, |
| \(f_N\) | összevont járműosztály forgalomfejlődési szorzója, az út forgalomba helyezési évétől számított t/2. évre az ÚT 2-1.118:2005 alapján, |
| \(ANF_i\) | az i-edik járműosztály átlagos napi forgalma [jármű/nap], |
| \(e_i\) | az i-edik járműosztály járműátszámítási szorzója, |
| \(a\) | egyes és csuklós autóbuszok, |
| \(n\) | nehéz tehergépkocsik, |
| \(p\) | pótkocsis tehergépkocsik, |
| \(ny\) | nyerges tehergépkocsik. |
A nehézgépjármű-forgalom főbb jellemzőinek vizsgálata
A tervezési forgalom meghatározásához szükséges adatok a valóságban időben és térben változóak. Az alábbiakban bemutatásra kerülnek az egyes paraméterek változékonyságai, és azok hatásai a tervezési forgalom értékére, illetve megbízhatóságára.
A jellemzők változékonysága
A közutak forgalmi, illetve célzottan nehézgépjármű-forgalmi adatainak elemzésére több hazai szakirodalmi elemzés megtalálható. A közúti forgalom összetételét elemezve Koren annak időbeli változását találta (Koren, 1997). Andricsák és munkatársai autópályák és az azokkal párhuzamosan haladó főutak forgalmi adatait vizsgálták, és azt találták, hogy ahol elérhető, a nehézgépjármű-forgalom átterelődik a főutakról az autópályákra, így az általuk vizsgált főutak nehézgépjármű-forgalma összességében csökkent (Andricsák, et al., 2005).
Koren és Thurzó egységjármű mértékegységben végzett kutatása során arra jutott, hogy a forgalom növekedése – változása – nem csak útkategóriák között, hanem régiónként is jelentősen eltérő (Koren & Thurzó, 2005). Timár a határmenti utak forgalmának előrebecslésén dolgozott, mely során az érintett utakon összességében a forgalom növekedését prognosztizálta, nemzetközi gazdasági és közlekedési adatok alapján (Timár, 2009).
A hazai forgalomszámlálási adatok és dinamikus tengelysúlymérési adatok (Weigh-in-Motion, WIM) elemzésében kiemelkedő Gulyás munkássága. Gulyás több éven keresztül figyelemmel kísérte a hazai WIM mérési adatok alakulását, és a tengelysúlyok alapján járműátszámítási szorzókat is többször meghatározott. A témában készült számos publikációja közül 2009-ben, a 2006 2007. évi adatok feldolgozása alapján a járműátszámítási szorzókat átlagértékük és relatív szórásuk megadásával publikálta. Eredményei alapján a legalacsonyabb relatív szórás 11%-ra adódott a leggyakrabban előforduló nehézgépjármű, az E2 jelű, „1+1+3” tengelyelrendezésű nyerges szerelvények esetében. A második és harmadik leggyakrabban előforduló nehézgépjármű esetében a relatív szórások rendre 39% és 37%-ra adódtak, míg a legmagasabb szórást a csuklós buszok esetében találta mintegy 84%-os értékkel (Gulyás, 2009). Később, szintén WIM adatok alapján, a tengelysúlyok időbeli növekedése is kimutatta (Gulyás, 2012a), melynek figyelembe vétele, vagy éppen elhanyagolása további bizonytalanságokat jelent a tervezési forgalom meghatározásában.
Kutatásom során a forgalom jellemzőit az útpályaszerkezet-méretezés során szükséges forgalmi terhelés meghatározása szempontjából vizsgálom, így, a több említett kutatáshoz hasonlóan kiválasztott autópályák és főutak által alkotott közlekedési folyosók nehézgépjármű-forgalmi adatait vizsgálom, az említett kutatásoknál részletesebb felbontásban. A szakirodalomban talált trendek, következtetések nehézgépjármű-forgalom tekintetében való igazolása céljából elemeztem négy hazai közlekedési folyosó nehézgépjármű-forgalmi adatait. Az eredményeket, összevont járműosztályok szerinti bontásban a 2. ábra mutatja, országos keresztmetszeti forgalomszámlálási adatokból levezetve.
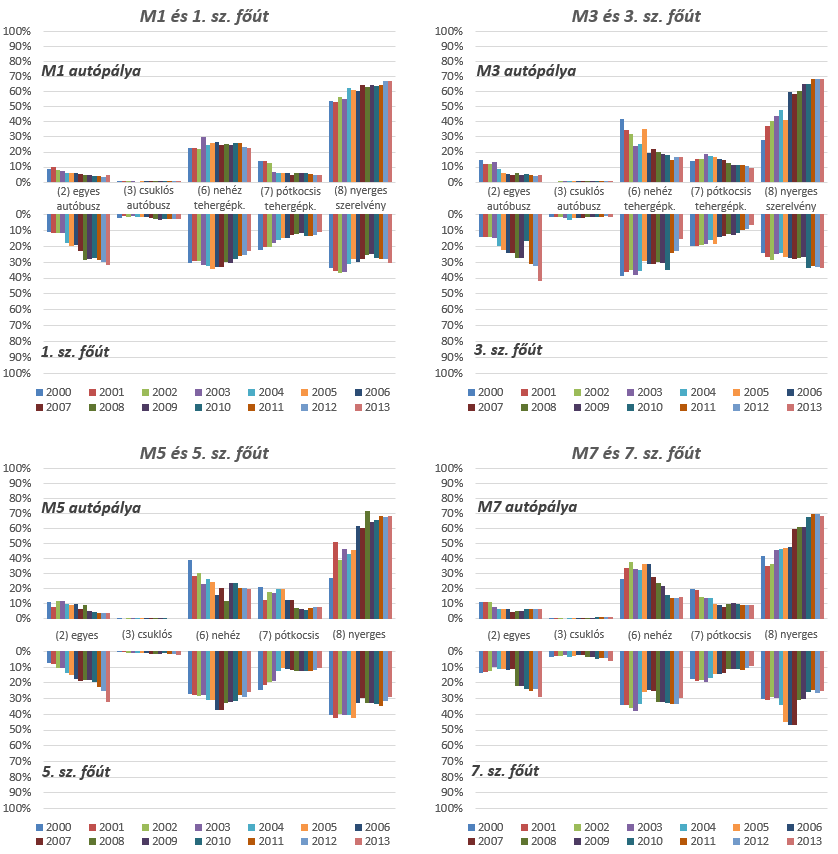 |
Az adatok nagyrészt alátámasztják a bemutatott szakirodalmi adatokat. Látható, hogy a nehézforgalom összetételében lényeges eltérések nem csak a vizsgált főutak és autópályák nehézforgalmi jellemzői között tapasztalhatóak, hanem az egyes főutak és egyes autópályák forgalma között is, ami hangsúlyozza a forgalom folyamatos figyelemmel kísérésének szükségességét. Látható a nehézforgalom átterelődése a főutakról az azokkal párhuzamosan futó autópályákra, és a nehézgépjármű-forgalom összetételének időbeli változása is. Itt fontos megjegyezni az útdíjpolitika változásait is, amely szintén hatással van az átterelődésre. Emellett, a 2. ábrán bemutatott adatok alapján végzett korábbi vizsgálataim során a forgalomfejlődési szorzó értéke az adatokat megyei bontásban feldolgozva, az egyes megyei útszakaszok nehézforgalmával súlyozva, a vizsgált autópályákra 1,89-re adódott a vizsgált időszakban (0,47-2,71 terjedelemmel), míg a vizsgált főutak esetén 0,67-re (0,26-0,83 terjedelemmel) (Soós, m.a.). Utóbbi esetben tehát a nehézforgalomból számítható egységtengely-szám – minden esetben – csökken – szemben a jelenleg érvényes előírásban feltételezett növekvő tendenciával (e-UT 02.01.31 [ÚT 2-1.118:2005], 2005). Ez a vizsgált autópályák esetében akár jelentős alulméretezést, a vizsgált főutak esetében akár jelentős túlméretezést is okozhat.
A változékonyság hatásai
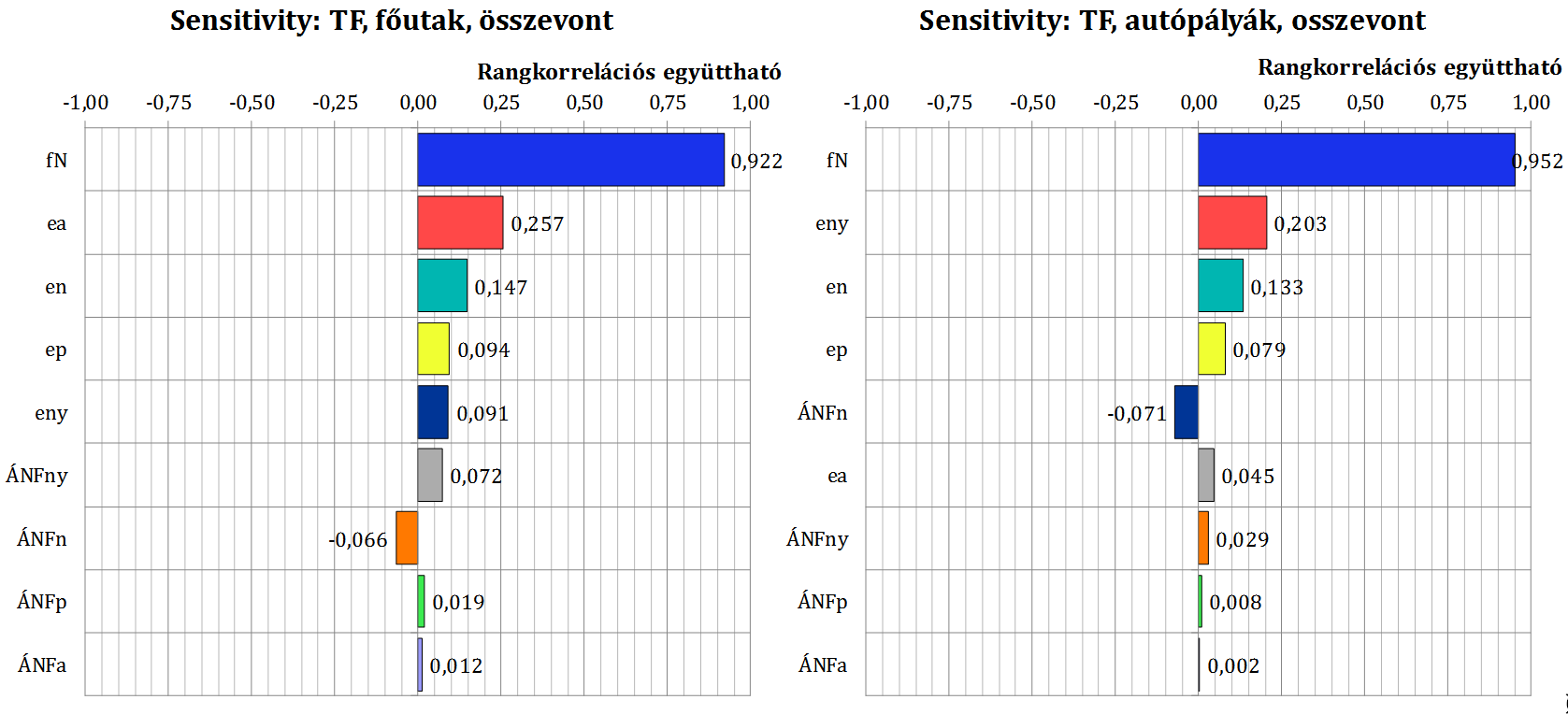
A vizsgálatok és szakirodalmak alapján talált változékonyságok felhasználásával a tervezési forgalom meghatározására használt összefüggéseket korábban érzékenységvizsgálatnak vetettem alá, melyben az ÚME szerinti diszkrét értékek helyett minden paramétert a valóságban előforduló értékeinek becsült gyakoriságával vettem figyelembe (Soós, 2016). Az érzékenységvizsgálat a rangkorrelációs együtthatók számításán és értékelésén alapult, amelyek azt mérik, hogy két sorozat – itt adott input paraméter és a végeredmény – mennyire változik együtt (Saltelli, 2002). Az eredményt a bemutatott összevont járműosztályokon alapuló számítás esetére a 3. ábra mutatja.
 |
| ahol: | |
| \(e_a\) | egyes és csuklós autóbuszok járműátszámítási szorzója, |
| \(e_n\) | egyes nehéz tehergépkocsik járműátszámítási szorzója, |
| \(e_p\) | pótkocsis szerelvények járműátszámítási szorzója, |
| \(e_{ny}\) | nyerges szerelvények járműátszámítási szorzója, |
| \(ANF_a\) | egyes és csuklós autóbuszok átlagos napi forgalma, |
| \(ANF_n\) | egyes nehéz tehergépkocsik átlagos napi forgalma, |
| \(ANF_p\) | pótkocsis szerelvények átlagos napi forgalma, |
| \(ANF_{ny}\) | nyerges szerelvények átlagos napi forgalma, |
| \(f_{N}\) | forgalomfejlődési szorzó. |
Az eredmények azt mutatták, hogy a végeredmény változékonyságát legjobban a forgalomfejlődési szorzó befolyásolja, autópályák és főutak esetében egyaránt. Könnyen belátható eredmény, hogy a nagyobb arányban előforduló járművek járműátszámítási szorzói jobban, a kisebb arányban előforduló járművek szorzói kevésbé befolyásolják az eredmény változékonyságát. Ezek autópályákon a nyerges, a nehéz és a pótkocsis gépkocsik, főutakon az autóbuszok és a nehéz gépkocsik.
A nehézforgalom jellemzőinek nyomon követésének fontossága tehát számítással igazolható, hiszen a forgalomnagyságon kívül egyéb jellemzők sem szükségszerűen változatlanok az idő vagy éppen a terület függvényében. Adott input adatok változékonysága végeredmény megbízhatóságát jobban befolyásolja, így ezek megbízható meghatározására a jövőben kiemelt figyelmet indokolt fordítani.
A forgalomfejlődési szorzóval, és általánosságban a forgalomfejlődés becslésének módszertanával külön elemzésben foglalkoztam (Soós, m.a.).
A járműátszámítási szorzók dinamikus tengelysúlymérési eredmények alapján való meghatározására módszert dolgoztunk ki (Soós, et al., m.a.), melynek lényege jelen cikkben röviden ismertetésre kerül, kiegészítve a szorzóval és a nehézgépjárművek rongáló hatásával kapcsolatos egyéb vizsgálatokkal.
A járműátszámítási szorzók vizsgálata
A járműátszámítási szorzók meghatározása
A járműátszámítási szorzó egy konkrét – vagy például egy adott járműosztályba tartozó reprezentatív járműnek – a 100 kN súlyú egységtengelyek áthaladási számában kifejezett rongáló hatását számszerűsíti, meghatározása a forgalomban nagyobb arányban részt vevő járművek esetén kiemelten fontos a tervezési forgalom meghatározása szempontjából.
Koren kutatásaiban határátkelőhelyeken és az ország belső területein elhelyezett tengelysúlymérlegek adataiból határozott meg járműátszámítási szorzókat (Koren, 1986), melyek értéküket tekintve némileg alacsonyabbak voltak az akkor hatályos méretezési utasításban megadott értékeknél (KPM, 1971). Később, a dinamikus tengelysúlymérő állomások telepítését követően (~1996), dinamikus tengelysúlymérési adatok alapján a szorzók többször felülvizsgálatra kerültek (Gulyás, 2002; Gulyás, 2009). Az, hogy Koren nem talált szignifikáns különbséget a határátkelők és belföldi utakon mért között, Gulyás az autópályák és főutak adatai között – mintegy másfél évtizeddel később – viszont igen, arra enged következtetni, hogy a nehézforgalom összetételében, a nagyobb részt nemzetközi forgalmú autópályák, és a nagyobb részt belföldi forgalmú főutak között, szignifikáns különbségek lehetnek. Ezt alátámasztani képes adatokról azonban nincs tudomásom.
A járműátszámítási szorzók meghatározására módszert mutattunk be, mely alkalmas a teljes tengelysúly-spektrum figyelembe vételére (Soós, et al., m.a.). A tengelysúly- és összsúly hisztogramok általában 2-3 lokális maximummal rendelkeznek (4. ábra), ami megnehezíti a statisztikai eszközök alkalmazását.
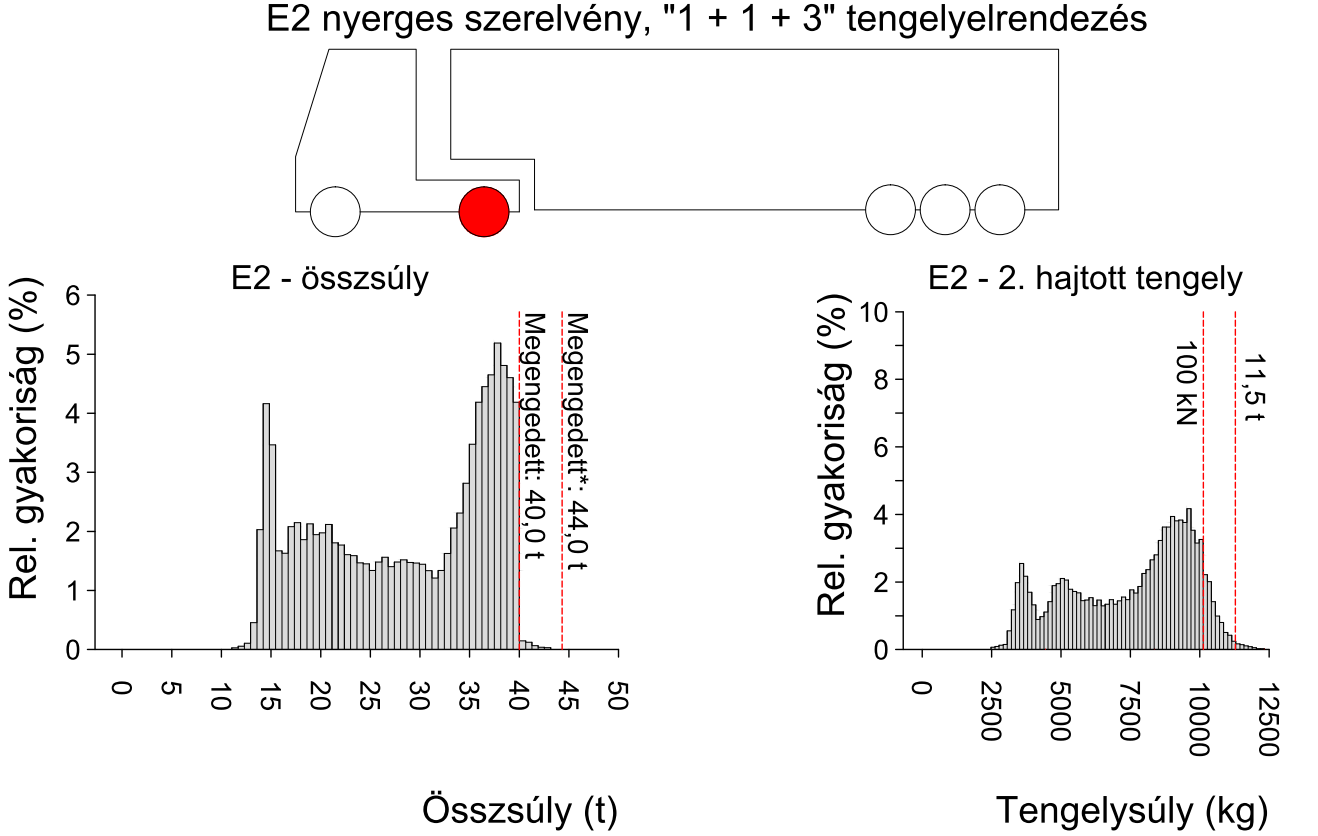 |
A javasolt módszer lényege, hogy a nevezetes eloszlásokkal nem leírható tengelysúly-hisztogramok a (2) egyenlet szerinti folytonos sűrűségfüggvénnyel három, egyenként normális eloszlásra való felbontással definiálhatóak. Ehhez hasonló megközelítés egy korábbi német kutatásban is fellelhető (BASt, 2009), melynek eredményei jól használhatóak a német analitikus pályaszerkezet-méretezési eljárás során.
\[p(x)={\pi}_1 f(x{\vert}{\mu}_1,{\sigma}_1^2 )+{\pi}_2 f(x{\vert}{\mu}_2,{\sigma}_2^2)+{\pi}_3 f(x{\vert}{\mu}_3,{\sigma}_3^2)\)\((2)\]
| ahol: | |
| \(p(x)\) | a közelítő függvény, |
| \({\pi}_2\) | az egyes normális eloszlások súlyszámai (∑πi=1), |
| \({\mu}_2\) | az egyes normális eloszlások várható értéke, |
| \({\sigma}_2^2\) | az egyes normális eloszlások tapasztalati szórásnégyzete. |
Az egyes normális eloszlások paraméterei – várható érték és szórás – és egymáshoz képest vett aránya például az ún. „E-M” algoritmus segítségével meghatározható, mely a függvényparamétereket a mérési adatsorhoz konvergálva, adott számú iteráció alatt becsüli (Dempster, et al., 1977). Az iterált paraméterekkel definiált \(p(x)\) függvény és az eredeti hisztogram közötti egyezőség értékelhető például a Cramér-von Mises próbával (Michael&Lei, 1996; Stephens, 1974). A vizsgálatok során az adódott, hogy legfeljebb néhány ezer iteráció után a számított \(p(x)\) függvény 0,97 feletti \(P\) értékkel közelíti az adatsort, ami gyakorlatilag egyezőséget jelent.
Adott \(i\)-edik járműtípus, \(j\)-edik tengelyéhez tartozó \(ej(x)\) rongáló hatás eloszlásfüggvénye, felhasználva a tengelysúly-hisztogramot közelítő sűrűségfüggvényt, a (3) egyenlet szerint számítható.
\[e_j(x)=\int_{0}^{\infty}\left(AF_{j}\dot{}BN_{j}\dot{}\frac{p(x)}{T_e}\right)^{h}dx\)\((3)\]
| ahol: | |
| \(e_j(x)\) | az i-edik járműtípus j-edik tengelyéhez tartozó rongáló hatás eloszlásfüggvénye, |
| \(AF_{j}\) | a j-edik tengelyen lévő abroncsok fajtájától függő korrekciós tényező, |
| \(BN_{j}\) | a j-edik tengelyen lévő abroncsok belső nyomásától függő korrekciós tényező, |
| \(p(x)\) | tengelysúlymérési eredményeket közelítő sűrűségfüggvény a (2) egyenlet szerint, |
| \(T_e\) | az egységtengely súlya, jelenleg \(T_e=100 kN=10,19 to\), |
| \(h\) | a pályaszerkezet-fárasztási (rongálódási) hatványkitevő, jelenleg \(h=5\). |
Az \(ej(x)\) folytonos eloszlásfüggvény alapján adott \(j\)-edik tengely rongáló hatása bármely kívánt megbízhatósági szinten meghatározható. Javasolva a szorzók megállapítása során korábban is alkalmazott 95%-os megbízhatósági szintet, a rongáló hatás keresett értéke azon \({e}_{j(95\%)}\) értéknél van, amelynél nagyobb legfeljebb 5% eséllyel fordulhat elő; azaz az \(e_{j}(x)\) függvény integrálja \(0-{e}_{j(95\%)}\) között éppen 0,95 (4. egyenlet). Természetesen más megbízhatósági szint is választható.
\[e_{i}=\int_{0}^{{e}_{j(95\%)}}e_{j(x)}dx=0,95\)\((4)\]
Az adott i-edik járműtípus járműátszámítási szorzója ezután a jármű n db tengelyére számított rongáló hatásának 95%-os megbízhatósági szinten vett értékének összegeként adódik az (5) egyenlet szerint.
\[e_{i}=\sum_{j=1}^{n}{e}_{j(95\%)}\)\((5)\]
Végül, 16 jellemző járműtípus \(e_i\) járműátszámítási szorzójának, valamint a nehézforgalomban képviselt arányuk ismeretében, számíthatóvá válnak a részletes, majd az összevont járműosztályokhoz rendelhető járműátszámítási szorzók, 95%-os megbízhatósági szinten. (Adatok hiányában az autóbuszok esetében külön elemzés szükséges, a módszer azonban változatlanul alkalmazható.) A számítások szerint alkalmazásra javasolt járműátszámítási szorzókat, 2014. évi WIM mérések alapján, az 1. táblázat tartalmazza.
| Járműtípus | Részletes járműosztály | Összevont járműosztály | ||||||
| Jel | Mérések száma | Járműátszámítási szorzó számított | Jel | Járműátszámítási szorzó | Jel | Járműátszámítási szorzó | ||
| Jelenlegi | Számított | Jelenlegi | Számított | |||||
| B | 0 | – | B | 1,3 | – | B | 1,30 | – |
| C1 | 167 966 | 0,30 | C1 | 0,5 | 0,30 | C | 0,60 | 0,34 |
| C21 | 5 788 | 1,51 | C2 | 1,0 | 1,51 | |||
| C22 | 28 | 2,03 | ||||||
| D11 | 13 434 | 1,31 | D1 | 1,3 | 1,70 | D | 1,60 | 2,07 |
| D12 | 12 733 | 2,11 | ||||||
| D21 | 10 933 | 2,23 | D2 | 2,5 | 2,20 | |||
| D22 | 489 | 1,44 | ||||||
| DX1 | 54 812 | 1,56 | DX | – | 2,14 | |||
| DX2 | 60 744 | 3,13 | ||||||
| DX3 | 16 122 | 0,35 | ||||||
| E11 | 5 966 | 0,59 | E1 | 0,8 | 0,79 | E | 1,70 | 1,81 |
| E12 | 214 371 | 0,8 | ||||||
| E2 | 1 797 771 | 1,94 | E2 | 1,8 | 1,94 | |||
| E31 | 667 | 2,09 | E3 | 2,6 | 1,92 | |||
| E32 | 70 | 0,27 | ||||||
| E4 | 2 452 | 1,49 | E4 | 1,4 | 1,49 | |||
A WIM adatok elemzése kapcsán felmerült három olyan, nagy számban előforduló jellemző jármű típus (1. táblázat, DX1, DX2, DX3), amelyet vonatkozó előírás közvetlenül nem tárgyal. Habár ezen járművek a keresztmetszeti forgalomszámlálások során a \(D\) összevont járműosztályban figyelembe vételre kerülnek, javasolható – például a részletes járműosztályokon vagy az ismert tengelysúlyokon alapuló számításokhoz – külön feltüntetése az előírásban.
A járműátszámítási szorzók időbeli változása
Korábbi elemzések (Gulyás, 2009) a nehézjárművek össz- és tengelysúlyainak időbeli növekedését mutatták ki, azonban – vélhetően – a változás mértéke okán az előírás ezt a tendenciát nem veszi figyelembe, ellentétben például a holland mintára készült dél-afrikai előírással, amely nem csak a forgalom, hanem járműátszámítási szorzó növekedési ütemét is figyelembe veszi (SAPEM, 2013). A 4.1. fejezetben bemutatott módszert a rendelkezésre álló 2008-2014 közötti adatokra alkalmazva, részletes járműosztályonként az 5. ábra szerinti eredmények adódnak. A részleteket a 2. táblázat tartalmazza.
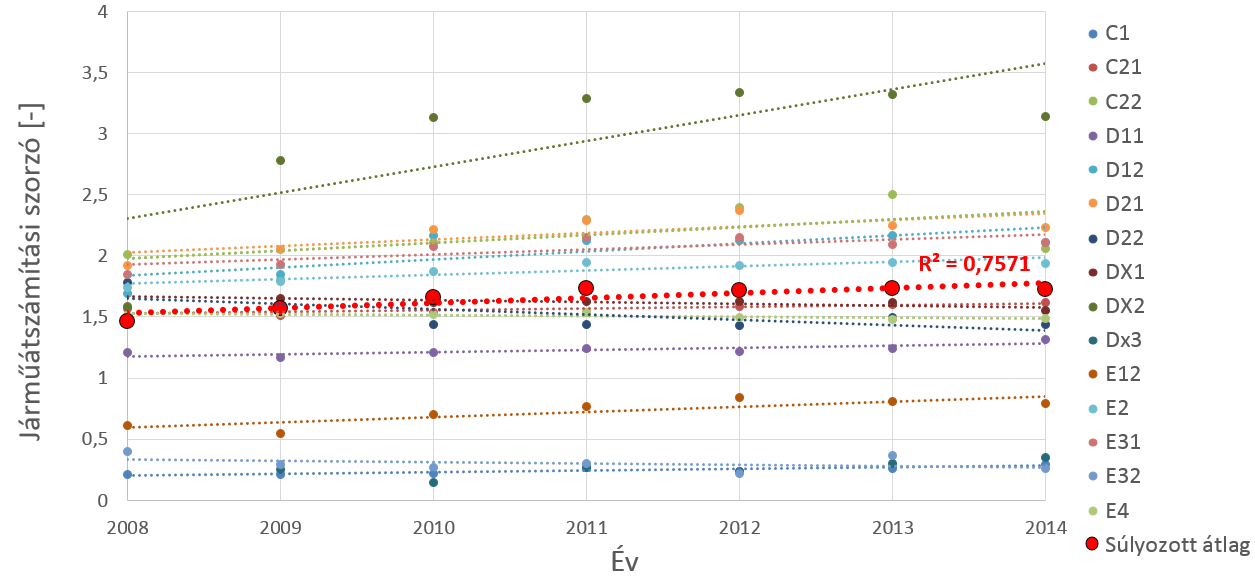 |
| Járműtípus | C1 | C21 | C22 | D11 | D12 | D21 | D22 | DX1 | DX2 | Dx3 | E11 | E12 | E2 | E31 | E32 | E4 | |
| Regr. egyenes (y=a+b*x) | a | -25,6 | -25,7 | -128,5 | -33,2 | -131,6 | -104,1 | 89,9 | 30,4 | -423,7 | -52,6 | 22,9 | -85,5 | -67,8 | -82,0 | 22,6 | 14,4 |
| b | 0,013 | 0,014 | 0,065 | 0,017 | 0,066 | 0,053 | -0,044 | -0,014 | 0,212 | 0,026 | -0,011 | 0,043 | 0,035 | 0,042 | -0,011 | -0,006 | |
| R2 | 0,779 | 0,564 | 0,338 | 0,643 | 0,579 | 0,555 | 0,531 | 0,602 | 0,536 | 0,540 | 0,619 | 0,723 | 0,785 | 0,607 | 0,144 | 0,413 | |
| Éves változás | 5,29% | 0,87% | 3,00% | 1,39% | 3,26% | 2,41% |
-2,89% |
-0,88% |
7,21% | 10,65% |
-1,87% |
5,92% | 1,84% | 2,04% |
-3,67% |
-0,43% |
|
A vizsgálat 11 járműtípus szorzója esetében növekedést, 5 járműtípus esetében csökkenést mutatott ki. A csökkenő rongáló hatást mutató járműosztályok, a DX1 kivételével a forgalomban igen alacsony arányt képviselnek, ezekben az esetekben az alacsony járműszám nem csak a gyenge korrelációt okozza, hanem a trend irányát is befolyásolhatja. Ugyanakkor mivel ezek a járműtípusok igen ritkán fordulnak elő a nehézforgalomban, részletesebb vizsgálatok nem kerültek elvégzésre.
Súlyozva az egyes járműosztályokhoz tartozó járműátszámítási szorzók alakulását a járműosztályok átlagos éves járműszámával, R2=0,76, közepes determinációs koefficienssel, lineárisan növekvő tendencia adódik, évi átlagos 2,56%-os ütemmel. Ez összhangban van Gulyás korábban publikált eredményeivel, miszerint a 2002-2004 és a 2008-2009 évi adatokat összehasonlítva a tengelysúlyok időbeli növekedését találta (Gulyás, 2012a) (Gulyás, 2012b), ám a tengelysúlyok vagy a járműátszámítási szorzók növekedését nem számszerűsítette.
Az eredményeket alátámasztandó, az EUROSTAT adatbázisból lekérdezésre kerültek a közúti szállítmányozásra vonatkozó főbb adatok. A nyilvántartásában rendelkezésre állnak jármű-kilométer és árutonna-kilométer adatok európai országonként és az EU-28 átlagára (összegére). Az adatokból becsülhető az átlagos tonna/jármű arány, melyet a 6. ábra szemléltet a nemzeti (belföldi), a nemzetközi és az összes áruforgalom esetére, Magyarországra és az EU-28-ra külön-külön. A vizsgálatok a komplett statisztikai adatsorokon történtek, melyek a WIM adatokhoz hasonlóan az ún. üres futást is tartalmazzák.
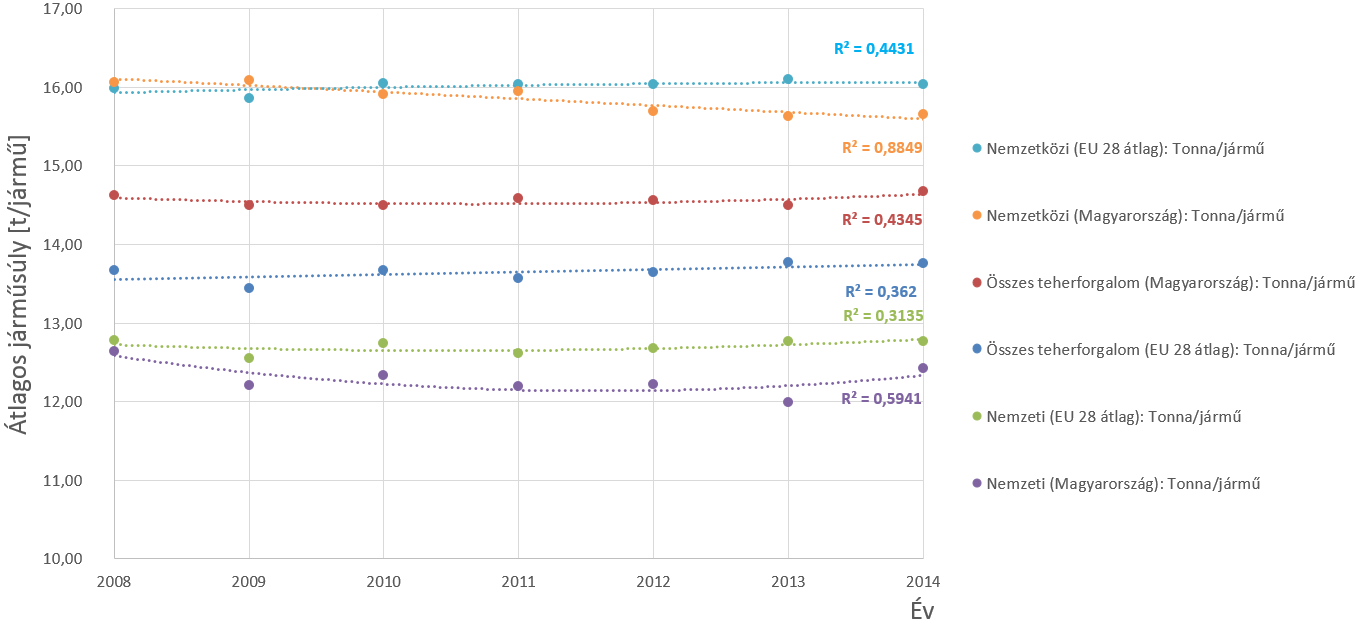 |
Az EU-28-ra vetített nemzetközi áruforgalom – alacsony determinációs koefficiens mellett növekvő trendje – összhangban van járműátszámítási szorzók WIM adatok alapján talált növekedésével, hogy az adatok határátkelőkről származnak, tehát a nemzetközi forgalomra vonatkoznak. Ezt összevetve a hazai eredetű nemzetközi áruforgalom csökkenő mutatójával megállapítható továbbá, hogy a határátkelőkön mért járművek túlnyomó többsége nem hazai eredetű nemzetközi forgalom.
Az ábrán látható, hogy a nemzetközi áruforgalom járművei az országon belüli áruforgalomnál 1-2 tonnával jobb kihasználtsággal közlekednek. Tekintve emellett, hogy a nemzetközi forgalom a belterületi úthálózatot célállomástól függetlenül terheli, a biztonság javára való közelítéssel a határátkelőkön mért adatokból számított járműátszámítási szorzók használhatóak a pályaszerkezet méretezés során.
A többlet fárasztó hatást figyelembe vevő szorzó
Magyarország Európai Uniós csatlakozása nyomán, megfelelve az EU 96/53/EK irányelvének, a hajtott egyes tengelyek megengedett legnagyobb súlya 10 t-ról 11,5 t-ra emelkedett, az ikertengelyek megengedett legnagyobb súlya 16 t-ról 18 t-ra emelkedett. A hármas tengelyek és a nem hajtott egyes tengelyek megengedett legnagyobb tengelysúlya 10 t ill. 24 t maradt.
Az irányelv szerinti és az azt megelőző (továbbiakban: korábbi) hazai szabályozás szerinti megengedett súlyhatárokat, járműtípusonként a 3. táblázat tartalmazza.
 |
A hazai útpályaszerkezeteket a korábban megengedett tengelysúly- ill. tengelycsoport-súlyokhoz képest növelt terhelésre felkészítendő, különböző Európai Uniós alapok támogatásával burkolatmegerősítési program indult (TRAFFICON, 2004). Feltételezhető volt, hogy a fuvarozók a lehetőséget kihasználva a korábbinál nehezebb járműveket fognak közlekedtetni, melynek hatásait, a tengelysúly-határ teljes kihasználását valószínűsítve, több tanulmányban vizsgálták. Például Timár a megnövelt tengelysúlyhatár hatásaként számításaiban – feltételezve annak teljes kihasználását – 8,5-11,5%-os várható élettartam rövidülést mutatott ki. Emellett – optimális burkolatgazdálkodást feltételezve – PMS modelleket alkalmazva 25 éves tervezési időszakra számítva, a hazai közúthálózaton mintegy 6,7%-os fenntartási költségnövekedést prognosztizált (Timár, 2005).
A változások hatásai a pályaszerkezet-méretezés során a tervezési forgalom meghatározása oldalán kerültek figyelembe vételre, egy ideiglenesen bevezetett „z” szorzó bevezetésével, melynek értékét előzetesen 1,5-re határozták meg. Később Gulyás, 2006-2007. évi WIM adatok elemzése alapján arra jutott, hogy a z=1,5 szorzó jó egyezést mutat a jelenlegi 10 tonnás és egy fiktív, 11,5 tonnás méretezési egységtengely alapján számított járműátszámítási szorzók arányával (Gulyás, 2009).
Mivel a szorzó a tengelyekre és tengelycsoportokra vonatkozó súlyhatár-emelés hatását hivatott figyelembe venni, a további számításokban a tandem és tridem tengelyek tengelycsoportként szerepelnek. A mérési adatokat a (2) egyenlet alapján leíró \(p(x)\) folytonos sűrűségfüggvény integrálásával kapott \(P(x)\) eloszlásfüggvény újabb integrálásával számítható annak a valószínűsége, hogy adott tengely ill. tengelycsoport súlya korábbi \((sh1)\) és a jelenlegi \((sh2)\) súlyhatár közé esik, a (6) egyenlet szerint, mely lényegében a súlyhatár-emelés következményét mutatja meg.
\[P_{1}((1)<T<(2))=\int_{0}^{sh2}P(x)\dot{}dx-\int_{0}^{sh1}P(x)\dot{}dx\)\((6)\]
| ahol: | |
| \(P_{1}\) | a korábbi hazai szabályozás és az uniós szabályozás közé eső tengelysúly előfordulási valószínűsége egy adott tengely vagy tengelycsoport esetében, |
| \({P(x)}\) | adott tengely vagy tengelycsoport súlyának eloszlásfüggvénye, |
| \((1)\) | az adott tengelyre vagy tengelycsoportra vonatkozó korábbi hazai szabályozás szerinti tengelysúlyhatár, |
| \((2)\) | az adott tengelyre vagy tengelycsoportra vonatkozó, 96/53/EK szerinti tengelysúlyhatár. |
Hasonlóképpen számítható egy adott tengely vagy tengelycsoport esetében a jelenlegi (sh2) súlyhatár meghaladásának valószínűsége a (7) egyenlet alapján, mely a túlsúly valószínűségét mutatja meg.
\[P_{2}(T>(2))=\int_{sh2}^{\infty}P(x)=1-\int_{0}^{sh2}P(x)dx\)(\(7)\]
A 4. táblázat a (6) és (7) egyenlet szerint számított valószínűségeket tartalmazza, tengely- illetve tengelycsoportonként, járműtípusonként.
 |
Látható, néhány esetben kiugróan magas a súlykorlát emelésének hatása, elsősorban a hajtott tengelyek esetében, ugyanakkor megjegyzendő, hogy a kevés mérésszámú E31 szerelvénytípus kivételével az ikertengelyek csak legfeljebb néhány százalékban lépik túl a korábban megengedett 16 tonna tengelysúlyt, a jelenleg megengedett 18 t tengelysúly irányába. A valószínűségek alapján, a 2014-ben mért járművek számát tekintve a súlykorlát emelésének hatására összesen mintegy 1 137 840 db tengely ill. tengelycsoport súlya lépte át a korábbi súlykorlátot, ami az összes mért tengely- és tengelycsoportnak (6 956 845 db tengely ill. tengelycsoport) jelentős, mintegy 16,4%-a, így részben alátámasztja a jelentős többlet-rongáló hatással kapcsolatos fenntartásokat.
A jelenlegi súlykorlátot túllépő tengelyek és tengelycsoportok számát tekintve megállapítható, hogy túlsúly jellemzően 1% alatti gyakorisággal fordul elő, kivéve a relatíve ritka E31 járműtípust, illetve a látszólag igen óvatlanul kihasznált, relatíve gyakran előforduló DX2 pótkocsis szerelvényt. A túlsúlyos tengelyek és tengelycsoportok száma mindössze 71.123 db. ami az összes mérés 1,02%-a.
Korábbi elemzések alapján a pályaszerkezet-méretezéshez használandó járműátszámítási szorzók szempontjából a tengelycsoportok tengelyenként való figyelembe vétele, ezáltal az egymás melletti tengelyek egymásra hatásának elhanyagolása, megengedhető közelítés (Koren, 1997; Gulyás, 1998). Ezt figyelembe véve az elemzéseket elvégezve úgy, hogy a tengelycsoportok egyedi tengelyekként kerülnek figyelembe vételre az adódott, hogy a 10 tonna feletti nehéztengelyek előfordulása mintegy 406 368 db., ami 3,71% relatív gyakoriságot jelent a 2014-ben mért összes tengely (10 964 374 db tengely) arányában.
A 4.1. fejezetben hivatkozott módszerrel meghatározott járműátszámítási szorzók a teljes tengelysúly-hisztogramok felhasználásával kerültek meghatározásra. Az összes (érvényes) mérés felhasználásával kapott tengelysúly-hisztogramokra, jó közelítéssel illesztett eloszlásfüggvények alapján számított értékek nem csak a súlyhatár emelésének hatására megnövekedett tengelysúlyokat, hanem a túlsúlyos járművek tengelyeinek rongáló hatását is figyelembe veszik. A tervezési forgalom meghatározása során jelenleg – útkategóriától függetlenül, illetve bel- és külterületen egyaránt alkalmazott „z” szorzóra tehát nincs szükség, ezáltal a jelenlegi, mintegy másfélszeres túlméretezést okozó hatása elkerülhető a fáradási élettartam szempontjából meghatározó, tervezési forgalom értékének megbízható meghatározása mellett.
A rongáló hatás kitevője
Az aszfaltburkolatú útpályaszerkezetek méretezésének korábbi empirikus gyakorlatát az 1960-as évek nagyléptékű AASHO kísérleteinek eredményei gyökeresen megváltoztatták. Az azóta „negyedik hatvány” (fourth power law) néven ismertté vált eredményeket már az első kiértékelések (Huff, et al., 1962) megfogalmazták. A pályaszerkezet teljesítőképességi indexének (PCI, Present Serviceability Index) alakulását vizsgálva a kutatók arra jutottak, hogy az egyes nehéztengelyek összesített pályaszerkezet-rongáló hatása az egységtengelyhez képest a 3,6-4,6 hatvánnyal arányos. Itt fontos megjegyezni, hogy az eredetileg vizsgált PCI nem csak a fáradási, hanem az összességében vett tönkremenetelre vonatkozó, tapasztalati jellegű mérőszám. Később számos újabb elemzés készült, például az Asphalt Institute kutatói nem sokkal később egy használhatóbb kiértékelést is közzétettek (Shook & Finn, 1962), mely lényegében a későbbi hazai szabályozás, a Hajlékony Útpályaszerkezetek Méretezési Utasítása – HUMU (KPM, 1971) alapját is jelentette.
Ez a megközelítés a mai napig számos ország gyakorlatában megtalálható, például a jelenlegi hazai mellett más országok méretezési előírásainak alapját képező német méretezési eljárásban is. Habár a COST 334 kutatás eredményei később tovább árnyalták a rongáló hatás leírását, miszerint a bitumenes kötőanyagú rétegek tönkremeneteléhez, fáradási repedések tekintetében 4-7 közötti, maradó alakváltozások esetén 1-2, míg az alapréteg maradó deformációjához 3-4 közötti hatványkitevő rendelhető (COST 334, 2001), a nehéztengelyek rongáló hatásának figyelembe vétele országonként eltérő maradt.
A korábbi hazai eljárás a tapasztalatokat meghonosítva, a nehéztengelyek egységtengelyhez képesti rongáló hatását, azaz a járműátszámítási szorzók értékeit a 4. hatvány szerint számította, mely összességében illeszkedett a különböző elemzésekben pályaszerkezet méretezéshez javasolt, 2-6 közé becsült hatványkitevőkhöz. A korábbi elképzelésekhez képest az 1990-es években a hazai szabályozás, a francia méretezési előírást az 5. hatványkitevő alkalmazására tért át. Ez a tervezési forgalom számítása során azzal jár, hogy az egységtengelynél kisebb súlyú tengelyek kisebb, az annál nagyobb súlyúak nagyobb rongáló hatással kerülnek figyelembe vételre (7. ábra).
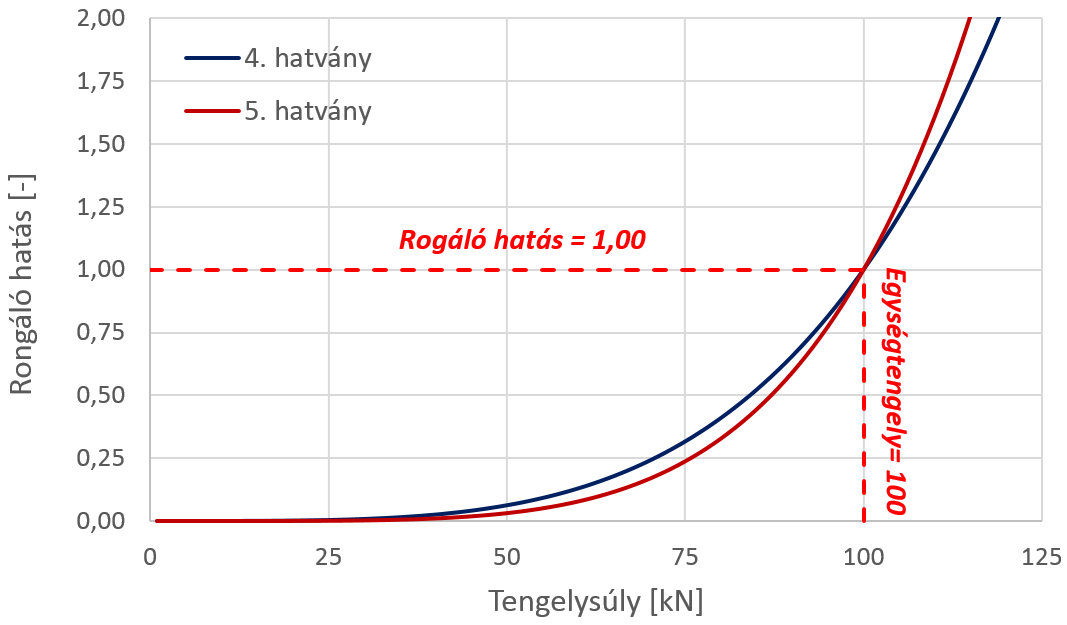 |
A már hivatkozott COST 334 kutatásban azt találták, hogy a 4-6 közötti rongáló hatás összességében helytálló, a forgalomban előforduló egyes nehéztengelyek relatív gyakoriságát is figyelembe véve, a két hatványkitevő alkalmazásával kapott egységtengely-áthaladási szám közötti különbség minimális. Ezt hazai számítások is alátámasztották (Gulyás, 1998), miszerint a kétféle kitevővel számított tervezési forgalmak közötti különbség 5% alatti (Gulyás, 2002).
Ennek ellenőrzésére, felhasználva a bemutatott módszertant, kiszámításra kerültek a járműátszámítási szorzók a 4. hatvány szerinti rongáló hatást feltételezve. Az eredményeket az alábbi 5. táblázat tartalmazza.
| Összevont járműosztály | ÚT
2-1-202:2005 |
Átlagos aránya a nehézgépjármű forgalomban | Járműátszámítási szorzó | |
| 4. hatvány szerint | 5. hatvány szerint | |||
| C | 0,6 | 7,35 % | 0,44 | 0,34 |
| D | 1,6 | 7,16 % | 2,11 | 2,07 |
| E | 1,7 | 85,49 % | 1,93 | 1,81 |
| Átlagos rongáló hatás: | 1,83 | 1,72 | ||
| Eltérés a 4. hatványhoz képest | 5,75% | |||
Látható, habár a kétféle kitevővel számított járműátszámítási szorzók értéke eltérő, tekintve a nehézgépjármű-osztályok arányát a nehézforgalomban, a különbség minimális, értéke összhangban van Gulyás eredményeivel. Az okozott eltérés a többi input adat hatásához képest elenyésző, így a hatványkitevő kérdésének értékelése pusztán a tengelysúlyadatok alapján nem lehetséges.
Összefoglalás
A tervezési forgalom meghatározására alkalmazott modellben a nehézforgalom térben és időben változó jellemzőinek figyelembe vétele érdekében jelentős egyszerűsítéseket, általánosításokat szükséges megtenni, ugyanakkor e jellemzők tervezési élettartam alatti változásainak lehető legpontosabb becslése elengedhetetlen az alul- illetve túlméretezés elkerülése, ezáltal a rendelkezésre álló erőforrások hatékony felhasználása szempontjából.
A tervezési forgalom meghatározásának pontosságára irányuló kutatásom során, elvégezve a modell érzékenységvizsgálatát, számszerű kimutatásra került, hogy az egyes input adatok valóságban előforduló változékonysága mekkora hatással van a végeredmény bizonytalanságára. Ezek közül a forgalomfejlődési szorzót, valamint a járműátszámítási szorzók vizsgálatait külön publikációkban mutattam be.
Jelen elemzés során a járműátszámítási szorzókat részletesebb vizsgálatnak vetettem alá. Felhasználva a korábban javasolt módszertant, vizsgálatra kerültek az egyes járműtípusok járműátszámítási szorzói az idő függvényében. Kimutatásra került, hogy a gyakoribb járműtípusok jellemzően növekvő, a ritkábbak jellemzően csökkenő járműátszámítási szorzókkal jellemezhetőek. Összességében, figyelembe véve az egyes járműtípusok arányát a nehézforgalomban, közepes korrelációval, lassú rongáló hatás növekedés mutatható ki.
Európai áruforgalmi statisztikák alapján nem csak a talált növekvő trend tekinthető igazoltnak, hanem az is, hogy a határátkelőkön történt WIM mérések alapján meghatározott járműátszámítási szorzók – a biztonság javára történő közelítéssel – alkalmazhatóak a belföldi közúthálózat méretezése során.
WIM adatok felhasználásával vizsgáltam a hajtott egyes tengely és a kettős tengelycsoport megengedett legnagyobb súlyának növekedéséből adódó többlet rongáló hatást figyelembe vevő „z” szorzót. A súlyhatár növelésének hatása egyértelműen kimutatható a WIM adatsorok leírására javasolt függvény elemzése alapján, ami igazolja a korábbi fenntartásokat a többlet rongáló hatással kapcsolatban. A cikkben javasolt módszertan alkalmazása esetén azonban a z szorzó nem szükséges, hiszen a járműátszámítási szorzók javasolt meghatározási módja szerint lehetőség nyílik a teljes tengelysúly-spektrum – így a törvényesen megnövekedett tengelysúllyal és a túlsúllyal közlekedő járművek – figyelembe vételére a járműátszámítási szorozók meghatározása során.
Vizsgálatra került a járműátszámítási szorzók meghatározásánál a nehéztengelyeknek az egységtengelyhez képest vett rongáló hatásának figyelembe vételére alkalmazott kitevő hatása. A kitevő értékének helyessége nem képezte a vizsgálat tárgyát, de annak hatását vizsgálva az adódott, hogy korábbi elemzések eredményei helytállóak, a nehézforgalom összetétele alapján nincs jelentős eltérés a negyedik és ötödik hatvány feltételezésével számított egységtengely-áthaladási számok között (az eltérés 5,75%). A rongáló hatás kitevőjének változása tehát a tervezési forgalom értéke szempontjából, a többi input adat hatását tekintve, elhanyagolható.
Hivatkozások
Ádány, S. és mtsai., 2007. Acélszerkezetek. Általános eljárások. Tervezés az EUROCODE alapján. 2. szerk. Budapest: Business Media Magyarország Kft..
Andricsák, Z., Gulyás, A. & Thurzó, G., 2005. Az autópályák és a párhuzamos főutak forgalmának alakulása a közelmúltban. Közúti és mélyépítési szemle 55:(8), pp. 15-21.
BASt, 2009. Auswirkungen des Schwerlastverkehrs auf die Brücken der Bundesfernstraßen. ISBN 978-3-86509-940-2.
COST 334, 2001. Effects of Wide Single Tyres and Dual Tyres. Final report of the action.
Deák, G. és mtsai., 2006. Terhek és hatások. Épületek tartószerkezeteinek tervezése az Eurocode alapján. Budapest: Business Media Magyarország Kft..
Dempster, A. D., Laird, N. M. & Rubin, D. B., 1977. Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society: Series B (Methodological) Vol. 39, No. 1., pp. 1-38.
e-UT 02.01.31 [ÚT 2-1.118:2005], 2005. Közutak távlati forgalmának meghatározása előrevetítő módszerrel. Magyar Útügyi Társaság, p. 20.
e-UT 06.03.13 [ÚT 2-1.202:2005]: , 2005. Aszfaltburkolatú útpályaszerkezetek méretezése és megerősítése. Magyar Útügyi Társaság, p. 34.
Farkas, G., Kovács, T., Lovas, A. & Szalai, K., 2015. A valószínűségi elven alapuló méretezés kialakulása hazánkban. asbeton: cikkgyűjtemény és köszöntések Dr. Tassi Géza egyetemi tanár, a műszaki tudományok doktora (MTA) születésének 90. évfordulója alkalmára, pp. 189-206.
Gulyás, A., 1998. Experience of Weigh-in-Motion in Hungary. Pre-Proceedings of the Second European Conference on Weigh-in-Motion of Road Vehicles, Lisbon, pp. 81-89.
Gulyás, A., 1998. Automatikus forgalmi adatgyűjtés és az eredmények többcélú felhasználása. Ph.D. értekezés, Budapesti Műszaki és Gazdaságtudományi Egyetem, Út és Forgalomtechnika Tanszék.
Gulyás, A., 2002. Az aszfaltburkolatú útpályaszerkezetek méretezésénél használatos járműátszámítási szorzók felülvizsgálata. Közúti közlekedés- és mélyépítéstudományi szemle 52(6), pp. 258-261.
Gulyás, A., 2009. Az elmúlt évek dinamikus tengelyterhelés-mérési eredményeinek vizsgálata. Közlekedésépítési szemle 59. évf. 5. szám, pp. 23-26.
Gulyás, A., 2012a. Axle load trends and their effects on pavement structural design. Pollack Periodica: An International Journal for Engineering and Information Sciences Vol. 7 No. 1, http://dx.doi.org/10.1556/Pollack.7.2012.1.9, pp. 97-106.
Gulyás, A., 2012b. Axle Load Trends in Hungary and their Effects on Pavement Structural Design. Procedia – Social and Behavioral Sciences 48:(6) doi:10.1016/j.sbspro.2012.06.1066, pp. 888-896.
Huff, T. S., Liddle, W. J. & Langsner, G., 1962. Use of Road Test Findings by AASHO Design Committee. HRB, National Research Council, Washnigton, D.C..
Karoliny, M., 2005. Minőség – új megközelítésben. Milyen lehetőségeket ad az EU?. Közúti és Mélyépítési szemle 55:(3), pp. 3-6.
Koren, C., 1986. A nehéz gépjárművek tengelysúly-összetétele és egységtengelyre való átszámítása hazánkban. Mélyépítéstudományi Szemle 36:(10), pp. 421-426.
Koren, C., 1987. Járműátszámítási szorzókmeghatározása a hajlékony útpályaszerkezetek méretezéséhez. Kandidátusi értekezés, Győr.
Koren, C., 1997. A nehéz forgalom időbeli és térbeli változásainak hatása a hazai úthálózaton. Közúti Közlekedési és Mélyépítéstudományi Szemle 47:(1) , pp. 18-25.
Koren, T. & Thurzó, G., 2005. Az országos közutak forgalmának alakulása. Közúti és mélyépítési szemle 55:(9), pp. 11-14.
KPM, 1971. Hajlékony Útpályaszerkezetek Méretezési Utasítása (HUMU), Közlekedés- és Postaügyi Minisztérium.
Michael I., J. & Lei, X., 1996. On convergence properties of the EM algorithm for Gaussian mixtures. Neural Computation 8:(1), pp. 129-151.
Saltelli, A., 2002. Sensitivity Analysis for Importance Assessment. Risk Analysis 22:(3) DOI:10.1111/0272-4332.00040, pp. 579-590.
SAPEM, 2013. South African Pavement Engineering Manual. első szerk. Republic of South Africa: South African National Roads Agency.
Shook, J. F. & Finn, F. N., 1962. Thickness Design Relationships for Asphalt Pavements. Proceedings of the international Conference on Structural Design of Asphalt Pavements.
Soós, Z., 2016. A tervezési forgalom meghatározásának vizsgálata sztochasztikus módszerekkel. Az Aszfalt: A Magyar Aszfaltipari Egyesülés (HAPA) Hivatalos Szakmai Lapja 20:(1), pp. 15-23.
Soós, Z., A forgalomfejlődés becslésének módszertana a valós forgalom és a nemzetközi gyakorlat tükrében. Budapest: Közlekedéstudományi szemle (Befogadva: 2015.12.15.) (megjelenés alatt).
Soós, Z., Tóth, C. & Bóka, D., m.a.. Determination of Load Equivalency Factors by Statistical Analysis of Weigh-In-Motion Data. The Baltic Journal of Road and Bridge Engineering (megjelenés alatt).
Stephens, M. A., 1974. EDF Statistics for Goodness of Fit and Some Comparisons. Journal of the American Statistical Association 69:(347), pp. 730-737.
Timár, A., 2005. A megengedett legnagyobb tengelysúly 11,5 tonnára növelésének hatásai. Közúti és mélyépítési szemle 55:(4), pp. 2-13.
Timár, A., 2009. A magyar úthálózatot igénybe vevő nemzetközi forgalom előrebecslése. Közlekedésépítési szemle (58):9, pp. 1-9.
TRAFFICON, 2004. Az országos közúthálózaton 2006 végéig megvalósuló 11,5 tonnás burkolat-megerősítési program végrehajtásának értékelése, figyelemmel a gyorsforgalmi úthálózat-fejlesztési programra. Kutatási jelentés.
