https://doi.org/10.36246/UL.2024.1.03
2024; 12. évfolyam, 19. szám
Elöljáróban
A hatályos magyar hídtervezési Útügyi Műszaki Előírás (e-UT 07.01.12:2011) a hasznos járműterheknél dinamikus többlet figyelembevételét írja elő, hasonlóan korábbi korok hídszabályzataihoz és számos más ország gyakorlatához.
Az első magyarországi hídszabályzatban is, ami 1910-ben jogszabályként jelent meg, szerepelt már dinamikus tényező, amivel a járműterheket kellett felszorozni, de igen egyszerűen, a támaszköztől függetlenül ennek nagyságát az előírás vas- és acélszerkezet esetében μ = 1,4 tényezővel, vasbeton szerkezet esetében pedig μ = 1,3 tényezővel rögzítette.
1935-ben jelent meg a második magyar közúti hídszabályzat „ideiglenes” jelzővel. Ekkor vezették be a támaszköztől függő dinamikus tényezőt.
\[ \mu=1,20+\frac{10}{30+l} \]
A következő, sorrendben harmadik közúti hídszabályzat, szintén „ideiglenes” jelzővel már a II. világháború után, 1950-ben jelent meg. Ebben csökkentették a dinamikus tényező értékét (1. ábra). Az akkor megállapított tényező a mai napig változatlanul érvényes.
\[ \mu=1,05+\frac{5}{5+l} \]
 |
Röviden bemutatom néhány további hídszabályzat szerinti előírást a dinamikus többlet figyelembe vételére, majd megvizsgálom, a szabályzat szerinti értékek használhatósági korlátait a különleges, túlsúlyos járművek vonatkozásában, mind civil, mind katonai esetet is elemezve.
Dinamikus tényező más előírásokban
A hatályos magyar Útügyi Műszaki Előírással jelenleg párhuzamosan érvényes és használható az Eurocode (MSZ EN 1990:2011) is a közúti hidak méretezéséhez. Napjainkban megjelenés előtt van a közúti hidak erőtani számítását tartalmazó új Útügyi Műszaki Előírás, ami több szempontból is paradigmaváltásként lényegében átveszi a hatályos Eurocode szerinti méretezési módszertant, attól csak néhány, tárgyi vizsgálatunk szempontjából nem releváns ponton eltérve (Bartus et al 2023; Hajós 2023).
Az Eurocode, és így a megjelenés előtt álló Útügyi Műszaki Előírás tervezet szövege sem tartalmaz alapesetben dinamikus tényezőt. Természetesen dinamikus hatás változatlanul terheli a hidakat, azonban az Eurocode szerinti ideális járműterhek intenzitását (sávonként alkalmazandó ikertengelyeket és ezekkel egyidejű megoszló terheléseket) úgy határozták meg, hogy azok már tartalmazzák a dinamikus többletet, ezért külön dinamikus tényezővel való növelés már nem szükséges.
Az Eurocode ezzel kétség kívül lényegesen egyszerűsíti a dinamikus hatás felvételét, mégpedig a támaszköztől, szerkezeti rendszertől, főtartó alapanyagtól függetlenül. Ennek következménye, hogy a hatályos szabályozáshoz képest, mikor nagyobb támaszközhöz kisebb dinamikus többlet tartozik, a globális biztonság a nagyobb támaszközök esetében elvileg kicsit magasabb lesz, mint kicsiny támaszközök esetén.
Az Eurocode-ban különleges tehereset a túlsúlyos járművek számítása. Mivel a túlsúlyos jármű alapértéke (mérlegelés, vagy rakodási terv alapján) nem tartalmaz dinamikus hatást, az Eurocode a túlsúlyos járművekhez ad csak meg dinamikus tényezőt, ami a támaszköz függvényében 1,4 és 1,2 között változik (2. ábra).
Példának a 2. ábrában megadtuk az Egyesült Államok előírását is: a dinamikus tényező hasonló a magyar előíráshoz, a legnagyobb értéke 1,4 helyett 1,3, viszont nagyobb nyílásoknál pedig 1-3%-kal nagyobb értéket ad meg.
 |
Vannak országok, ahol külön előírás érvényes az acél és a vasbeton hidakra. Erre példa a kínai hídtervezési előírás. Kínában az acélhidak dinamikus tényezője lényegében azonos az amerikaival, de a vasbeton hidak dinamikus tényezője (2. ábra) sokkal kisebb, 45 m fölött pedig nem kell a dinamikus hatást figyelembe venni.
Kanadában a dinamikus tényezőt a híd sajátfrekvenciájának függvényében kell meghatározni 1,2 és 1,4 között.
A dinamikus hatás vizsgálata
A mozgó közúti jármű és a híd kölcsönhatása a statikus terheléshez képest többlet terhelést okoz, ezt mint láttuk, jellemzően önálló dinamikus tényezővel vagy a járműteher felvett alapértékének növelésével vesszük számításba. A dinamikus hatást a valóságban természetesen sok tényező befolyásolja, a híd és a jármű együttes dinamikus modellezése sokparaméteres rendszerekkel közelíthető. A hídszerkezetet terhelő dinamikus hatás függ a jármű rugózásától, csillapításától, kerekeinek számától, a jármű sebességétől, a jármű tömegétől, a jármű hosszától és szélességétől, a jármű aktuális műszaki állapotától, a híd támaszközétől, a híd sajátfrekvenciájától, a híd csillapításától, a híd önsúlyától, a kocsipálya hibáitól – s e sort még lehetne folytatni.
A hídtervezési előírásokban a dinamikus hatást hasonlóan minden más számított hatáshoz, egyszerűsítik. Mint bemutattam, számos tervezési előírásban a dinamikus tényező egyszerűen a támaszköz függvénye, nagyobb támaszközhöz kisebb dinamikus tényező tartozik. A dinamikus hatást befolyásoló többi tényezőt az előírások nem veszik figyelembe.
Minél nagyobb a hasznos jármű tömege, számszerűsítve annál nagyobb a dinamikus többlet hatás értéke, ezért érdemes megvizsgálni azt, hogy a normál járművek esetében figyelmen kívül hagyott paraméterek közül van-e olyan, ami a különleges, túlsúlyos járművek vizsgálatakor felértékelődik.
A dinamikus hatás pontos számítása igen összetett modellezést eredményezne, továbbá ilyen elemzés során már csak korlátozottan alkalmazható Hook törvénye, a jármű és a híd is nem lineárisan rugalmasan viselkedik, részben viszkóelasztikus modellezést kellene használni.
A dinamikus hatást befolyásoló egyik legjelentősebb paraméter a jármű „rugózása”. A híd ellenőrzését civil forgalomban nem végezhetjük el különféle járműtípusokra (például más legyen a híd teherbírása mezőgazdasági traktorra és más nyergesvontatóra), viszont civil különleges túlsúlyos járművek és katonai terhelés esetén lehetséges ilyen szempontú differenciálás is.
A járműrugózás hatására egy egyszerű példa a mezőgazdasági traktor (például MTZ-80, önsúly 3600 kg). Egyetlen könnyű mezőgazdasági traktor képes belengetni egy 100 m nyílású acélhidat. Ennek oka, hogy az amúgy könnyű, kéttengelyes MTZ-80 rugózása adott esetben hatékonyan gerjeszti a vizsgált acélhidat.
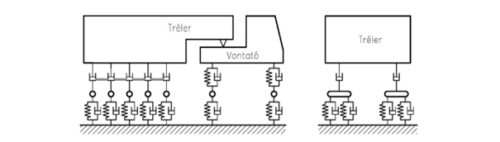
Megfigyelhetjük a jármű felfüggesztésének típusából eredő különbségeket is. A hagyományos teherautóknak légrugózása van, s az abroncs is érdemi csillapított rugózásra képest (3. ábra).
 |
A 3. ábrán lévő dinamikai modellben látható oldalnézetben és keresztmetszetben az egyes tengelyeket a jármű alvázához kapcsoló csillapított rugók, valamint a tengelyeken lévő kerekek, mint önálló csillapított rugók.
Ha egy közúti járműnek a normál teherautókhoz képest (40 tonna) lényegesen nagyobb a tömege (100 tonna felett), akkor annak jellemzően több tengelye is van, melyek egy közös merev alvázhoz kapcsolódnak. Ez már önmagában kedvezőbb, azaz kisebb dinamikus többletet eredményez, mivel a több független csillapított rugózás óhatatlanul részben egymást is csillapítja azáltal, hogy a közös merev felépítményt alátámasztó több tengely megtámasztottsága közvetett módon kölcsönösen egymásra kihat.
A dinamikus hatás szempontjából további jelentős előnyökkel jár a túlsúlyos szállításokhoz kifejlesztett, soktengelyes járműveknek különleges, olajhidraulikus felfüggesztési rendszere. A civil és a katonai nehéz közúti szállítójárművek ma már többségében olajhidraulikus felfüggesztésűek (4. ábra).
 |
A 4. ábrán lévő jelölések: 1. rövidtengely mechanikus kormányrúdja; 2. kormányzást biztosító forgórész; 3. olajhidraulika; 4. kerék helye; 5. fékhenger.
Az olajhidraulikus felfüggesztés esetén a tengelyeket egy-egy olajhidraulika kapcsolja az alvázhoz, amelyek közös hidraulikakörre vannak kapcsolva. Ha az egyik hidraulika összenyomódik, akkor az onnan távozó hidraulikaolaj megjelenik többi hidraulikánál többlet lökethosszt eredményezve. Ezáltal az összekapcsolt tengelyek terhelése kiegyenlítődik.
A Heavy-Duty Modules tréler modulárisan egymáshoz sorolható tengelyeit legtöbbször három, egyes esetekben négy hidraulikus körbe szerelik (5. ábra). Egy-egy hidraulikus körön belül a tengelyek terhelése egyenlő.
 |
Három hidraulikakör esetén a három kör egy-egy függőleges eredővel helyettesíthető, amelyek így határozott rendszert képeznek a jármű terhelésének felvételében.
Minél nagyobb egy jármű teljes tömege, annál több tengelye van. Például, ha a jármű össztömege 250 tonna, akkor tipikusan van 22 tengelye. Az ilyen jármű hosszú is, például 35 m. Belátható, hogy egy ilyen jármű és a híd együttes dinamikai modellje, kölcsönhatása teljesen más, mint a kéttengelyes könnyű mezőgazdasági traktoré. Egyrészt a tengelyeknek a rugózása egészen más, mint a légrugós tengelyeké, másrészt sok tengely rugózása egymást részben kiegyenlíti. Kimondható, hogy minél nagyobb egy jármű teljes tömege, annál kisebb lesz a dinamikus hatása.
A hidraulikus felfüggesztésű járműveknek nincsen „hintázó” mozgása, ugyanakkor rugózásuk keményebb, kedvező tulajdonságaik elsősorban kis sebességnél jelentősek.
A hagyományos jármű 3. ábrán szereplő dinamikai modelljének mintájára az olajhidraulikus körbe rendezett nehézgépszállító tréler dinamikai modelljét szemlélteti a 6. ábra.
Kisebb dinamikus többletet eredményez, hogy a túlsúlyos járműveknek sok tengelye van. További előnyökkel jár, hogy a nehézgépszállító trélerek két oldali kerekei önálló felfüggesztésű rövidtengellyel kapcsolódnak az alvázhoz. A dinamikai modellben szereplő kerekek csillapított rugózása is kedvezőbb, mert keresztirányban négy vagy nyolc gumiabroncs közel egyenletesen támasztja alá a járművet, így az úthibákból származó hatások is kisebbek lesznek, mert a jármű nagyobb felületen érintkezik az útburkolattal.
 |
Lánctalpas járművek dinamikus hatásáról
Eddig csak a kerekes járműveket vizsgáltuk. A katonai járművek jelentős rész nem kerekes, hanem lánctalpas.
Egyetlen hídtervezési szabályzat sem ad eltérő tényezőket a lánctalpas járművekhez (STANAG 2021; AEP-3.12.1.5 NATO Standard). A magyar előírásokban nincs lánctalpas jármű méretezésére vonatkozó hídtervezési szabályozás (MSZ EN 1990:2011; e-UT 07.01.12:2011). Külön vizsgálat nélkül az Egyesült Államokban és Kanadában a katonai járművekhez 1,15-ös dinamikus tényezőt javasolnak.
A lánctalpas járművek dinamikus többlethatását Antonty Everitt szakdolgozatában kísérleti mérésekkel elemezte. Összehasonlította négy katonai jármű dinamikus hatását ugyanazon a hídszerkezeten. A kísérletet Kanadában, 29,6+32,9 m támaszközű közúti hídon végezték. Három különböző kerekes járművet (50,4 tonna össztömegű, öttengelyes nehézgépszállító tréler, 27,5 tonna össztömegű, négytengelyes és 26,1 tonna össztömegű háromtengelyes katonai jármű) és egy 63,2 tonna össztömegű Leopard 2 harckocsit használtak a mérésekhez.
Everitt az útpálya esetleges egyenetlenségét az útpályára helyezett fapalló akadályokkal modellezte. Összesen 90 különféle áthaladási esetet mértek meg a négy járművel. Ezek között volt hibátlan útpályával készített mérés és a fapalló akadályokkal modellezett sérült útpályával készített mérés is. A méréseket 10, 20, 30, 40 és 50 km/h sebességgel készítették.
A vizsgálat eredménye azt mutatja, hogy a kerekes járművek dinamikus hatása hibátlan útfelület esetén másfélszerese a lánctalpas járműnek, akadályokkal modellezett sérült útpálya esetén pedig ötszöröse volt a lánctalpas járműhöz képest.
Lenner doktori disszertációjában a lánctalpas járművek dinamikus tényezőjét részletesen vizsgálja. Közli Homberg ajánlását, aki kutatását 1970-ben végezte. A dinamikus tényezőt lánctalpas járművek esetében 1,1-értékben maximalizálta.
A lánctalpas járművek fejlődéstörténetét és sokféleségét részletesen bemutatta Farkas Zoltán nyolcrészes cikksorozatában. Vizsgálatunk szempontjából kedvező, hogy a jelenleg használatos nagy tömegű katonai járművek (Leopárd harckocsi) felfüggesztése és így dinamikus hatása a híd szempontjából legkedvezőbbek közé tartozik. Régebbi típusú, híd szempontjából kedvezőtlenebb rugózású katonai járművek száma lényegesen kisebb és ezek tömege is kisebb, így nem okoznak mértékadó terhelést.
Érdemes megemlíteni, hogy a lánctalpas járművek teherátadását a felfekvési felületen egyenletesen megoszlónak tekintjük, bár tudjuk, hogy ez a valóságban nem minden esetben igaz. Mivel jellemzően a lánctalp felfekvési hosszúsága rövid (például 5 m), a lánctalpon belül meglévő egyenetlenségek globális hatása nem jelentős, ezért ez elhanyagolható. Érdemi hatása csak kis nyílású hidaknál és lokális vizsgálatoknál lehetne, de ezekben az esetekben bizonyosan a szóló tengely lesz a mértékadó terhelés és nem a lánctalp, így a lánctalpon belüli egyenetlenségek a híd szempontjából elhanyagolhatók.
Javaslatok
Javaslom a különleges túlsúlyos civil és katonai járművek dinamikus tényezőjének csökkentését. A pontosításhoz további kutatások és elsősorban kísérleti mérések szükségesek. A kedvező eredményeket az eddigi vizsgálatok igazolják, csökkentett tényező általános alkalmazásához további mérések szükségesek.
A bemutatott irodalom alapján javaslom a kísérletek elvégzéséig és kiértékeléséig, a lánctalpas járművek dinamikus tényezőjét 1,1 értékben maximálni. A jármű és a híd kölcsönhatásának szükséges részletesebb elemzése után javaslom a 1200 kN feletti kerekes járművek esetében is maximalizálni a dinamikus tényezőt 1,1 értékkel, amennyiben a sebesség legfeljebb 40 km/h.
Irodalomjegyzék
[1]: AEP-3.12.1.5 NATO Standard Military Load Classification of bridges, ferries, rafts and vehicles. Edition A Version 1, September 2017;
[2]: Bartus, R., Kővári, Á. & Németh, G. 2023: Észrevételek és javaslatok a készülő új e-UT 07.01.12 közúti hidak erőtani számítása – Útügyi Műszaki Előíráshoz. Útügyi lapok, 11(18), 19 https://doi.org/10.36246/UL.2023.2.01
[3]: e-UT 07.01.12:2011 Erőtani számítás, Közúti hidak tervezése (KHT) 2. Útügyi Műszaki Előírás, Online: https://ume.kozut.hu/dokumentum/205
[4]: Escribano-Garcia, R, Bobadilla, M, Somovilla Gómez, F, Ahmed, A, (2020): A Theoretical Model with Which to Safely Optimize the Configuration of Hydraulic Suspension of Modular Trailers in Special Road Transport. In Applied Sciences, Vol. 11.
[5]: Everitt, Antony (2019): Dynamic load effects of tracked and wheeled military vehicles from bridge load testing. A Thesis Submitted to the Division of Graduate Studies of the Royal Military College of Canada, MASc Thesis Document;
[6]: Farkas, Z. (2017): Lánctalpas futóművek I. rész. In Haditechnika, 51 (5). pp. 64-68. https://doi.org/10.23713/HT.51.5.14
[7]: Farkas, Z. (2017): Lánctalpas futóművek II. rész. In Haditechnika, 51 (6). pp. 62-65. https://doi.org/10.23713/HT.51.6.13
[8]: Farkas, Z. (2018): Lánctalpas futóművek III. rész. In Haditechnika, 52 (1). pp. 55-60. https://doi.org/10.23713/HT.52.1.12
[9]: Farkas, Z. (2018): Lánctalpas futóművek IV. rész. In Haditechnika, 52 (2). pp. 54-58. https://doi.org/10.23713/HT.52.2.12
[10]: Farkas, Z. (2018): Lánctalpas futóművek V. rész : A lánctalpas járószerkezet. In Haditechnika, 52 (3). pp. 64-67. https://doi.org/10.23713/HT.52.3.14
[11]: Farkas, Z. (2019): Lánctalpas futóművek VI. rész. In Haditechnika, 53 (5). pp. 70-75. https://doi.org/10.23713/HT.53.5.15
[12]: Farkas, Z. (2019): Lánctalpas futóművek VII. rész. In Haditechnika, 53 (6). pp. 67-71. https://doi.org/10.23713/HT.53.6.14
[13]: Farkas, Z. (2020): Lánctalpas futóművek VIII. rész. In Haditechnika, 54 (1). pp. 69-75. https://doi.org/10.23713/HT.54.1.14
[14]: Hajós B. (2023): Szempontok és javaslatok a közúti hídtervezés hasznos ideális jármű teherszintjének meghatározásához a készülő új Útügyi Műszaki Előírásban, Útügyi lapok, 11(18), 14 https://doi.org/10.36246/UL.2023.2.03
[15]: Homberg, H. 1970. Berechnung von Brücken und Militärlasten, Band 1, STANAG 2021 Norm für militärische Fahrzeuge und Brückenbelastungen, Werner-Verlag GmbH, Düsseldorf;
[16]: Lenner, R. (2014): Safety Concept and Partial Factors for Military Assessment of Existing Concrete Bridges. PhD dissertation, Universität Der Bundeswehr München, Fakultät für Bauingenieurwesen und Umweltwissenchaften;
[17]: MSZ EN 1990:2011 Eurocode: A tartószerkezetek tervezésének alapjai
[18]: STANAG 2021 Standardization Agreement, Military Load Classifica-tion of bridges, ferries, rafts and vehicles. Edition 8, 14 September 2017 NSO/1074 (2017) MILENG/2021;
Erre a szövegre így hivatkozhat:
Hajós Bence: A közúti hidak dinamikus tényezőjének csökkentési lehetőségei túlsúlyos civil járművek és nehéz katonai szállítások esetén, 2024, DOI: 10.36246/UL.2024.1.03
