https://doi.org/10.36246/UL.2020.2.02
2020; 8. évfolyam, 14. szám
Pdf: A klimatikus jellemzők hatásai az útpályaszerkezetre: A pályaszerkezet hőmérsékletek számítása
Bevezetés
A környezeti jellemzők (főként a hőmérséklet, a csapadék, a légnedvesség, a fagyás-olvadás ciklusok és a talajvíz mélysége) jelentős hatást gyakorolnak az útburkolatokra így a pályaszerkezetek méretezésénél is fontos tényezőként vehetők figyelembe (Gupta, 2014). Különösen fontos a környezeti jellemzők alaposabb vizsgálata az alsóbbrendű vagy mezőgazdasági utaknál, az erdők feltáróhálózatánál, valamint az agro-erdészeti rendszerek kiszolgáló útjainál, mivel ezeknél az úthálózatoknál az időjárásnak való kitettség a vékonyabb pályaszerkezet miatt erőteljesebben is érezteti hatását. Pethő (2008) mérései azt mutatták, hogy konkrétan a szélsőségesen alacsony és magas hőmérsékletek fordulnak elő gyakrabban, mint a magasabb terhelési kategóriákban (vastagabb pályaszerkezetekben).
A környezeti jellemzők közül 3 változását célszerű figyelembe venni a hajlékony pályaszerkezetek méretezésénél:
- Az aszfalt rétegek hőmérsékletének változásai. Ez a paraméter azért lényeges, mert az aszfaltkeverékek modulusai nagyon érzékenyek a hőmérsékletváltozásra.
- Az alsó rétegek (elsősorban a földmű) talajnedvességének változásai. A földmű moduluszok általában az optimális talajnedvességre és sűrűségre (tömörségre) vonatkoznak. Sok esetben viszont az optimálistól eltérő jellemzőkre korrekciós faktorok szükségesek (Zapata, 2018).
- A fagyás olvadás jelensége és ennek ciklusai igen jelentősen befolyásolják az alsó rétegek és a földmű teherbírását. Hiszen a fagyos periódusok alatt a földmű teherbírása nő, míg az olvadási periódusok alatt jelentősen csökken, tehát a fagyás mélységének és az egyes olvadási ciklusok egymásra következésének ismerete is egy fontos kérdés.
Az előbbiek szerint tehát az aszfaltburkolatú pályaszerkezetek tartósságának számításánál, az egyszerűen meghatározható és általában könnyen elérhető meteorológiai paraméterek közül, a hőmérséklet, annak ingadozása és a csapadék a figyelembe vehető tényezők (Boromissza, 1997). Az Útügyi Lapok folyóirat 13. lapszámában közölt: „A klimatikus jellemzők hatásai az útpályaszerkezetre” című kézirat dolgozta fel e két paraméter általános változási tendenciáit Magyarországon, figyelembe véve a klímaváltozást.
Jelen cikk pedig a pályaszerkezet hőmérsékletek számításának lehetőségeivel foglalkozik.
A pályaszerkezet hőmérsékletek számítása
Az aszfaltkeverékek, mint viszkoelasztikus anyagok merevségi modulusai jellemzően az aszfalt összetételétől, a terhelési frekvenciától, és a hőmérséklettől, mint környezeti tényezőtől függenek. A beépített aszfaltrétegek modulusa, tehát erősen a hőmérséklet függvénye is.
A pályaszerkezet hőmérsékletére hatást gyakorló paraméterek
A pályaszerkezet vertikális hőmérsékleti eloszlása alapvetően a következő jellemzőktől függ: 1, időjárási körülmények (dinamikusan változnak), 2, az egyes pályaszerkezeti rétegek és az alépítmény hővezetési hőraktározási jellemzői (inkább statikusak, bár a nedvességtartalom jelentősen befolyásoló hatással bírhat (Zapata, 2018)).
A pályaszerkezet felszínén jellemző hőmozgás alapvetően energiaháztartási alapon határozható meg. A felszínre az energiamérleg a következő formában írható fel (Dingman, 2002):
\[R_{n}=G-H-LE=\frac{d_{Q}}{d_{dt}}\]
| \(R_{n}\) | = | A felszínre vonatkozó sugárzási egyenleg, amely a beérkező és távozó rövid és hosszúhullámú sugárzás egyenlege [W/m2]. Elsősorban a beérkező globál sugárzástól, a felszín albedójától, valamint rövid és hosszúhullámú sugárzás elnyelő képességétől függ (Pethő, 2008) |
| \(G\) | = | a talaj felé irányuló hőáram, amely a talajban tárolt hőmennyiségtől és a köztes rétegek hővezető képességétől függ [W/m2] |
| \(H\) | = | a szenzibilis hőcsere az atmoszférával, a környező levegő felmelegítése vagy lehűtése [W/m2] |
| \(LE\) | = | az atmoszféra felé irányuló látens hőáram (párolgás), csak a csapadékesemények alatt, ill. közvetlenül utána van jelentősége [W/m2] |
| \(\frac{d_{Q}}{d_{dt}}\) | = | a raktározott hőmennyiség megváltozása a felszíni rétegben [W/m2] |
A felszín energiaháztartását a következő 1. ábra illusztrálja.
 |
Az előbbi hőháztartási egyenlet alapján a klimatikus viszonyok mérése mellett elviekben a pályaszerkezet hőmérséklete a kívánt mélységben meghatározható. Természetesen a rendelkezésre álló paraméterek valós értékének ismerete elengedhetetlen a pontos meghatározáshoz.
A pályaszerkezet hőmérséklete valamilyen mértékben követi a környezet hőmérsékleti változásait, így rövid távon (napon belül, órás léptékben) és hosszú távon (szezonálisan) is ingadozik. Azonban nemcsak az aktuális sugárzási viszonyok és a levegőhőmérséklet, hanem a csapadék és a légmozgás is, mint klimatikus befolyásoló faktorok megjelennek. Ezenkívül az alsóbb pályaszerkezeti rétegek hőmérséklete (és hővezetése) is befolyásolja a felszín közeli pályaszerkezeti rétegek hőmérsékletét (Pethő, 2008).
Az előbbiek közül talán a napból érkező és a felszín jellemzőitől függően hasznosuló sugárzás emelendő ki, mint a pályaszerkezet hőmérséklet eloszlásnak egyik legfontosabb eleme (Pethő, 2008).
A pályaszerkezet függőleges hőmérsékleti eloszlására ható tényezőket Pethő (2008) a következőkben sorolja fel:
- Léghőmérséklet,
- Besugárzás,
- Építőanyagok termo-fizikai jellemzői,
- A felület szóró, elnyelő és reflektáló tulajdonságai,
- A szél intenzitása.
A burkolatfelszín és a mélyebb rétegek hőmérséklete különböző termodinamikai, fizikai és meteorológiai folyamatok eredménye. Ezen folyamatok ismerete és vizsgálatokon alapuló megértése nagyon fontos ahhoz, hogy információkat nyerjünk pályaszerkezetünk hőmérséklet viselkedéséről (Ureczky és Tóth, 2008).
Ha vannak méréseink az adott pályaszerkezetre vonatkozóan, akkor általában a pályaszerkezet hőmérsékletét, célszerű alapul venni, de felmerül a kérdés, hogy milyen mélységre számítsunk, vagyis, hogy milyen mélységben értelmezett hőmérsékletet értünk a pályaszerkezet hőmérséklet alatt. A méretezés szempontjából a különböző forgalmi terhelés osztályokhoz rendelt teljes aszfalt típus pályaszerkezetek alsó rétegének középső síkjában számított hőmérsékleteket célszerű vizsgálni (Pethő, 2008).
Pethő (2008) az adott pályaszerkezet típus alsó rétegének középsíkjában mért hőmérséklet, illetve az alsó szál megnyúlása között igen szoros (R2≈0,98-0,99), összefüggést határozott meg. A léghőmérséklettel is elvégezte az összefüggés-vizsgálatot. Az eredmények szerint az összefüggés szorossága gyengült, de még mindig (minden esetben R2> 0,84) erős függvénykapcsolat állt fenn a jellemzők között. Az összefüggés létrehozásához felhasznált mérési adatok gyakorisága perces volt, tehát relatíve nagy időbeli felbontású.
A léghőmérséklet és a megnyúlás között fennálló relatíve gyengébb kapcsolatot azzal magyarázza, hogy a vizsgált alsóbb réteg hőmérséklete a léghőmérsékletet időbeli késéssel és erősen csillapítva követi. A csillapítás mértéke a mélység növelésével nő, viszont a szélsőséges kiugró értékek is ellapulnak. Felmerül a kérés azonban, hogy ha nem perces felbontású, hanem pl. havi adatokat használunk fel a méretezéshez, akkor a korábban említett időbeli késésnek van –e jogosultsága. Szezonális elemzéseknél a léghőmérséklet és a pályaszerkezet hőmérséklete közötti fáziskésés nem vagy alig jelentkezik, így a két jellemző közötti hiszterézis hatással nem kell kalkulálni, elég a csillapítást számítani.
Pethő (2008) is megjegyzi munkájában, hogy a pályaszerkezet hőmérséklet adatok csak korlátozottan állnak rendelkezésre (a mérés kivitelezése sem olyan könnyű), míg a léghőmérséklet mérése jó területi eloszlásban és nagy gyakorisággal történik, így a léghőmérsékleti adatok felhasználásával létrehozott összefüggésekre nagyobb az igény.
Általánosan használt pályaszerkezet hőmérséklet becslő egyenlet
Ha nem állnak rendelkezésre a pályaszerkezet hőmérsékletére vonatkozóan mérések, akkor az adott jellemző mélységben a hőmérséklet napon belüli változásának figyelembevételéhez sokszor a burkolat felületi hőmérsékletét és a megelőző nap hőmérsékletét veszik figyelembe, mint az általánosan használt BELLS2 egyenletnél (Drumm & Meier, 2003).
\[T_{d}=B_{0}+B_{1}\cdot T_{s}+(log_{10}(d)-1,25)\cdot (B_{2}\cdot T_{s}+B_{3}\cdot T_{a(1-nap)}+B_{4}\cdot f_{a})+B_{5}\cdot T_{s} \cdot f_{b} \]
| \(T_{d}\) | = | a pályaszerkezet hőmérséklete az adott d [mm] mélységben [°C] |
| \(T_{s}\) | = | a felszín hőmérséklete (infravörös hőmérővel mért eredetileg) [°C] |
| \(T_{a}\) | = | (1-nap), a mérést megelőző nap átlagos léghőmérséklete [°C] |
fa és fb – az időbeli késést figyelembe vevő korrekciós faktorok, lásd részletesebben Stubstad et al. (1998).
B0 – B5 – az egyenlet paraméterei az USA-ban megadott kalibrációs paraméterekre a következőek: B0=2,78; B1=0,912; B2=-0,428; B3=0,553; B4=2,630; B5=0,027 (Fernandó et al. 2001). Az USA-n belül Texas (5 pont és 2 szelvény), Új Mexikó (1 pont) és Oklahoma (1 pont) állomok területén voltak a mérési pontok, így jellemzően e mérési helyekre kalibráltak a paraméterek.
Általában azonban nem áll rendelkezésre a burkolathőmérséklet. Ilyen esetben a napközbeni órákra vonatkozóan, mikor általában a forgalom is döntő mértékben zajlik, és a burkolathőmérséklet magasabb, mint a léghőmérséklet a következő egyszerű összefüggést fejlesztették ki a pályaszerkezet hőmérsékletének becslésére (Ullidtz, 1998):
\[T_{p}=1,2\cdot t_{a} + 3,2\]
| \(T_{p}\) | = | a pályaszerkezet napközbeni átlagos hőmérséklete [°C] |
| \(T_{a}\) | = | a napközbeni léghőmérséklet [°C] |
A hivatkozott irodalom sajnos nem közli, hogy az összefüggés milyen mélységben, vagy milyen vastagságú pályaszerkezetre érvényes, így konkrét számításra kevésbé használható.
Maximum és minimum hőmérsékletek számítása
Ahogy azt korábban leírtuk, a hőmérséklet szélső értékei sokszor kritikusak, így ezekre vonatkozóan is kidolgoztak összefüggéseket. A következő számítási eljárásnál a minimum és maximum hőmérsékletbecslésre is nyílik lehetőség a pályaszerkezet adott mélységben, napi időlépcsőben. A kidolgozott összefüggésben a felszínt érő sugárzás mennyiségét (pl. globálsugárzás) is felhasználják általában a levegőhőmérséklet értékek mellett. A Deiefenderer et al. (2006) által kidolgozott módszer általános alakja első megközelítésben a következő volt:
\[T_{p}=a+b\cdot T_{a}+c\cdot Y + d \cdot P_{d} \]
Ahol:
| \(T_{p}\) | = | a pályaszerkezet hőmérséklete [°C] |
| \(P_{d}\) | = | mélységben [m] |
| \(a\) | = | tengelymetszet |
| \(b\) | = | a környezeti hőmérsékletre vonatkozó korrekciós tényező |
| \(T_{a}\) | = | környezeti hőmérséklet [°C] |
| \(c\) | = | az év napjaira vonatkozó korrekciós tényező |
| \(Y\) | = | az év napjai (1 tól 183-ig). Az év napjainak megadása az év első felében (Január 1-től július 2.-ig) lineárisan növekedett 1-től 183-íg. Az év második felében pedig ugyancsak lineárisan csökkent 182-ről 1-re (július 3-tól december 31.-ig). Szökőévekben egy nap hozzáadása történt meg az értékekhez |
| \(d\) | = | a mélységre (Pd) vonatkozó korrekciós tényező |
Az év napjainak megadása a modell kezdeti állapotában a sugárzási paraméter (pl. globálsugárzás) helyettesítésére történt meg. A felparaméterezett kezdeti egyenlet azonban csak a kalibrálás helyén volt érvényes.
Az eljárás továbbfejlesztése során az év napjainak megadása helyett már egy adott földrajzi helyre számítható, sugárzási paraméter bevonása történt meg az egyenletbe, a napi minimum és maximum aszfalthőmérsékletek becslése céljából. Az USA Virginia államában kidolgozott és ott validált modellek paraméterekkel ellátva a következők:
Maximum hőmérséklet:
\[T_{psmax}= 2,78752 + 0,6861\cdot T_{max}+5,6736\cdot10^{-4}\cdot R_{s}-27,8739\cdot P_{d} \]
Minimum hőmérséklet:
\[T_{psmin}= 1,2097 + 0,6754\cdot T_{min}+3,7642\cdot10^{-4}\cdot R_{s}-7,2043\cdot P_{d} \]
Ahol a korábban nem szereplő paraméterek:
| \(T_{psmax} és T_{psmin}\) | = | a pályaszerkezet Pd mélységben számított napi minimum és maximum hőmérséklete |
| \(R_{s}\) | = | az adott helyre számított globálsugárzás (kJ/m2/nap) |
| \(T_{max} és T_{min}\) | = | mint a környezet jellemző napi maximum és minim hőmérséklete |
A globálsugárzás számítása sok esetben bonyolultabb, több lépésben elvégezhető eljárás, ezért az adott hely földrajzi szélességét, mint a globálsugárzást kiváltó, de mégis helyspecifikus paramétert vonták be a végső modellbe. A kidolgozott, most már egyszerűen és általánosan (a föld felszínén bármely ponton) használható egyenlet a következő:
Maximum hőmérséklet:
\[T_{plmax}= 6,0775 + 1,1265\cdot T_{max}+0,001820\cdot Y_{d} +0,0839 \cdot L – 53,5247 \cdot P_{d} \]
Minimum hőmérséklet:
\[T_{plmin}= 27,5986 + 0,9608\cdot T_{min}+0,0641\cdot Y_{d} +0,5616 \cdot L + 9,4893 \cdot P_{d} \]
Ahol a korábban nem szereplő paraméterek:
| \(L\) | = | a földrajzi szélesség (fokban) |
| \(Y_{d}\) | = | az év napja (most már 1-től 365-ig) |
A fenti egyenletek 0,8-0,85 közötti R2 értékkel tudták becsülni a burkolathőmérsékleteket (Deiefenderer et al., 2006) tehát általában elfogadható pontosságúnak minősülnek. A hibák inkább a maximum hőmérsékletek esetében jellemzőbbek és általában az aszfalthőmérsékletek alábecslésében jelentkeznek. A minimum hőmérsékletek viszonylag pontosabban becsülhetők az egyenletekkel.
A fenti egyenlet a maximális és minimális napi léghőmérséklet ismeretét igényli.
Szezonális becslés
Megfontolandó, ha aszfalt merevségi modulusait csak szezonális, havi felbontásban akarjuk meghatározni, nem elegendő–e egy egyszerűbb, kevesebb paramétert bevonó egyenlet kidolgozása.
Az előbbi probléma-megoldási módszert a kevesebb paraméter mellett más is indokolja. Hazai viszonyok között végzett behajlásmérések hőmérsékletfüggésének vizsgálatánál Ureczky & Tóth (2008) azt találták, hogy a léghőmérséklettel szorosabb a tárcsaközép behajlás (és így a merevségi modulus) összefüggése, mint a burkolatfelszín hőmérsékletével. A burkolatfelszín hőmérséklet emellett elég heterogén (a felszín időszakos árnyékoltságától, egyenetlen szerkezetétől, albedójától, mikrodomborzatától is nagymértékben függ) is lehet és kevéssé hozzáférhető adat, mint a standard 2 méteres árnyékolt szenzorral mért levegőhőmérséklet.
Az amerikai irodalom is a havi szintű, a pályaszerkezet mélyebb rétegeire vonatkozó, hőmérsékletbecslésnél egyszerű léghőmérsékleten, mint egyetlen független változón, alapuló összefüggést javasol a megoldásra (George & Hussian, 1986; Asphalt Institute,1982).
Az Asphalt Institute (1982) javaslata szerint (eredetileg Witczak (1972) összefüggését alapul véve) az egyes mélységekben az aszfalthőmérsékleteket a következő egyenlet megfelelő pontossággal becsli (terepi vizsgálatok szerint R2=0,89-0,93 a mélységgel növekvő korreláció mellett:
\[MMPT=MMAT\cdot(1+\frac{1}{\frac{z}{2,54}+4})-\frac{10}{9\cdot(\frac{z}{2,54+4})}+\frac{10}{3} \]
Ahol:
| \(MMPT\) | = | az aszfalt hőmérséklete a megadott z [cm] mélységben [°C] |
| \(MMAT\) | = | a levegőhőmérséklet 2 méteres magasságban [°C] |
Az egyenlet működésére illusztrációként az 1, 10 és 30 cm mélységekben számolt aszfalthőmérsékleteket feltüntettük a 2. ábrán a léghőmérséklet függvényében.
 |
A Pethő (2008) a léghőmérséklet és a pályaszerkezet alsó rétegének súlypontjában mért hőmérsékletek között a fenti Asphalt Institute (1982) által kidolgozott egyenletnek megfelelő összefüggést talált. A paraméterek annak ellenére nagyon hasonlóak, hogy az egyik perces mérésekből dolgozott, a másik összefüggés pedig havi adatokon alapult (1. táblázat).
| Forgalmi terhelési osztály | Mélység | Pethő (2008) | AI (1982) | ||
| Z [cm] | Meredekség | Tengelymetszet | Meredekség | Tengelymetszet | |
| C | 14,5 | 1,1246 | 1,9218 | 1,1030 | 3,2189 |
| D | 17 | 1,0965 | 2,2386 | 1,0935 | 3,2294 |
| E | 19 | 1,0778 | 2,4492 | 1,0871 | 3,2365 |
| K | 23 | 1,0448 | 2,7775 | 1,0766 | 3,2482 |
A két összefüggést azonos alakúra hozva, a 1. táblázat alapján látható, hogy az alkalmazott lineáris kapcsolatok iránytangense csak a második tizedesben, a tengelymetszetek pedig a legfelső kategóriát kivéve (a felső 14,5 cm-es mélységben 1,3 Celsius fok) 1 Celsius fokon belül vannak.
A fenti AI (1982) egyenlethez teljesen hasonló formájú összefüggést közöl George és Hussian (1986) az aszfalthőmérsékletek havi szintű becsléséhez.
\[MMPT=MMAT\cdot(1+\frac{7,62}{z+30,48})-\frac{8,47}{z+30,48}+3,3 \]
| \(MMPT\) | = | az aszfalt hőmérséklete a megadott z [cm] mélységben [°C] |
| \(MMAT\) | = | a levegőhőmérséklet 2 méteres magasságban [°C] |
Adatszegény esetben a havi átlagos léghőmérséklet becslésére használható összefüggés
Abban az esetben, ha az adott helyre vonatkozóan még léghőmérsékleti adatok sem állnak idősor formájában rendelkezésre, ill. a meteorológiai állomások nagyon távol (több száz km) helyezkednek el a mérési ponttól, akkor egyszerű pl. cos hullámon alapuló becslést vesznek alapul. Az eljárásra, amennyiben az adott időlépcsőben érvényes hőmérsékleti szélsőségek legalább becslésszerűen ismertek, szolgáljon például a következő heti átlaghőmérsékleteket becslő összefüggés (Ullidtz, 1998):
\[T_{a}=\frac{(T_{max}+T_{min})}{2} + \frac{(T_{max}-T_{min})}{2}\cdot cos\frac{(U-U_{o})\cdot P_{i}}{26}+3,3 \]
Ahol:
| \(T_{a}\) | = | az átlagos levegőhőmérséklet az U-val jelölt héten [°C] |
| \(T_{min} ill. T_{max}\) | = | a jellemző heti maximum és minimum hőmérséklet az adott régióban [°C] |
| \(U_{0}\) | = | az a hét, ahol a maximális léghőmérséklet (heti átlagban) előfordul |
Az egyenlet havi átlaghőmérsékletek becslésre is alkalmas lehet, de ebben az esetben az U adott hónapot, az U0 pedig a Tmax, maximális átlaghőmérsékletű hónapot jelöli. Havi becslésnél a cos-os tag nevezőjében 26 helyett 6 szerepel és természetesen a Tmin, minimális hőmérséklet is havi szinten értendő.
Az aszfalt modulusok és a hőmérséklet kapcsolata
Az aszfalt merevségi modulusa és hőmérsékletek között kidolgozott összefüggések általában exponenciálisak, ami felhívja a figyelmet a hőmérsékletnek, mint változónak a fontosságára a méretezésben. Az AASHTO (1993) által kidolgozott összefüggés például:
\[logE_{ac}=6,451235-0,000164671\cdot T_{p}^{1,925244} \]
Ahol:
| \(E_{ac}\) | = | az aszfalt merevségi modulusa (Apshalt Concrete Elastic Modulus) |
| \(T_{p}\) | = | az aszfalt hőmérséklete az adott mélységben [°C]. |
Hasonló és igen szoros (R2=0,98) exponenciális összefüggést talált Pethő (2008) a megnyúlás és a pályaszerkezet alsó rétegének hőmérséklete között.
Magyarországra jellemző méretezéshez szükséges hőmérsékleti értékek és azok változása az időben
A számításokhoz szükséges léghőmérséklet adatsorokat kutatási célra a szabadon hozzáférhető FORESEE adatbázis felhasználásával állítottuk elő.
Az amerikai Shell módszerben (Claessen et al., 1977) a havi levegőhőmérsékletekből indulnak ki, az alapján számolják. Az Asphalt Institute (Witczak, 1982) megközelítés szerint az adott mélységben az aszfalthőmérsékleteket és azokat egy súlyszámmal látják el a léghőmérsékletek alapján a következő összefüggés szerint:
\[WF=0,0763\cdot exp(0,1328\cdot MMAT) \]
Ahol:
| \(WF\) | = | a súlyszám (dimenzió nélküli) |
| \(MMAT\) | = | a levegőhőmérséklet 2 méteres magasságban [°C] |
Az adott földrajzi helyre vonatkozólag a havi súlyszámok alapján meghatároznak egy átlagos súlyszámot. Végül pedig az átlagos súlyszám alapján határoznak meg egy ekvivalens hőmérsékleti értéket.
Az összefüggéshez csak a havi átlagos levegőhőmérsékletek szükségesek. Ezeket megadjuk a múlt jelen és jövő 30 éves periódusaira összesítve a 2. táblázatban. Láthatjuk, hogy az előbbi összefüggés szerint a nyári periódusra eső súlyszámok jelentősen nagyobbak, mint a téliek. Az előbbiekből következően a nyári magasabb hőmérsékletű hónapok hatása fokozottabban jelentkezik az ekvivalens hőmérsékletek számításánál.
| Hónap | 1951-1980 | 1981-2010 | 2016‑2045 | |||
| MMAT | WF | MMAT | WF | MMAT | WF | |
| Jan. | -1,88 | 0,06 | -0,57 | 0,07 | -0,05 | 0,08 |
| Febr. | 0,88 | 0,09 | 1,45 | 0,09 | 2,81 | 0,11 |
| Már. | 5,24 | 0,15 | 6,09 | 0,17 | 6,64 | 0,18 |
| Ápr. | 10,75 | 0,32 | 11,68 | 0,36 | 12,26 | 0,39 |
| Máj. | 15,45 | 0,59 | 16,73 | 0,70 | 17,45 | 0,77 |
| Jún. | 19,07 | 0,96 | 19,63 | 1,03 | 20,48 | 1,16 |
| Júl. | 20,49 | 1,16 | 21,68 | 1,36 | 22,77 | 1,57 |
| Aug. | 19,98 | 1,08 | 21,26 | 1,28 | 22,56 | 1,53 |
| Szept. | 16,23 | 0,66 | 16,74 | 0,70 | 18,06 | 0,84 |
| Okt. | 10,85 | 0,32 | 11,55 | 0,35 | 13,01 | 0,43 |
| Nov. | 5,39 | 0,16 | 5,25 | 0,15 | 5,87 | 0,17 |
| Dec. | 0,58 | 0,08 | 0,66 | 0,08 | 1,44 | 0,09 |
Az aszfalthőmérsékletek alapján történő merevségi modulus becsléséhez bizonyos méretezési eljárásoknál hőmérsékleti eloszlásokat használnak. A francia méretezi eljárásnál 5 fokos osztályközönként adják meg a hőmérsékleti eloszlásokat és így számítják egy segédprogram segítségével a mértékadó aszfaltmodulust (French Design Manual, 1997).
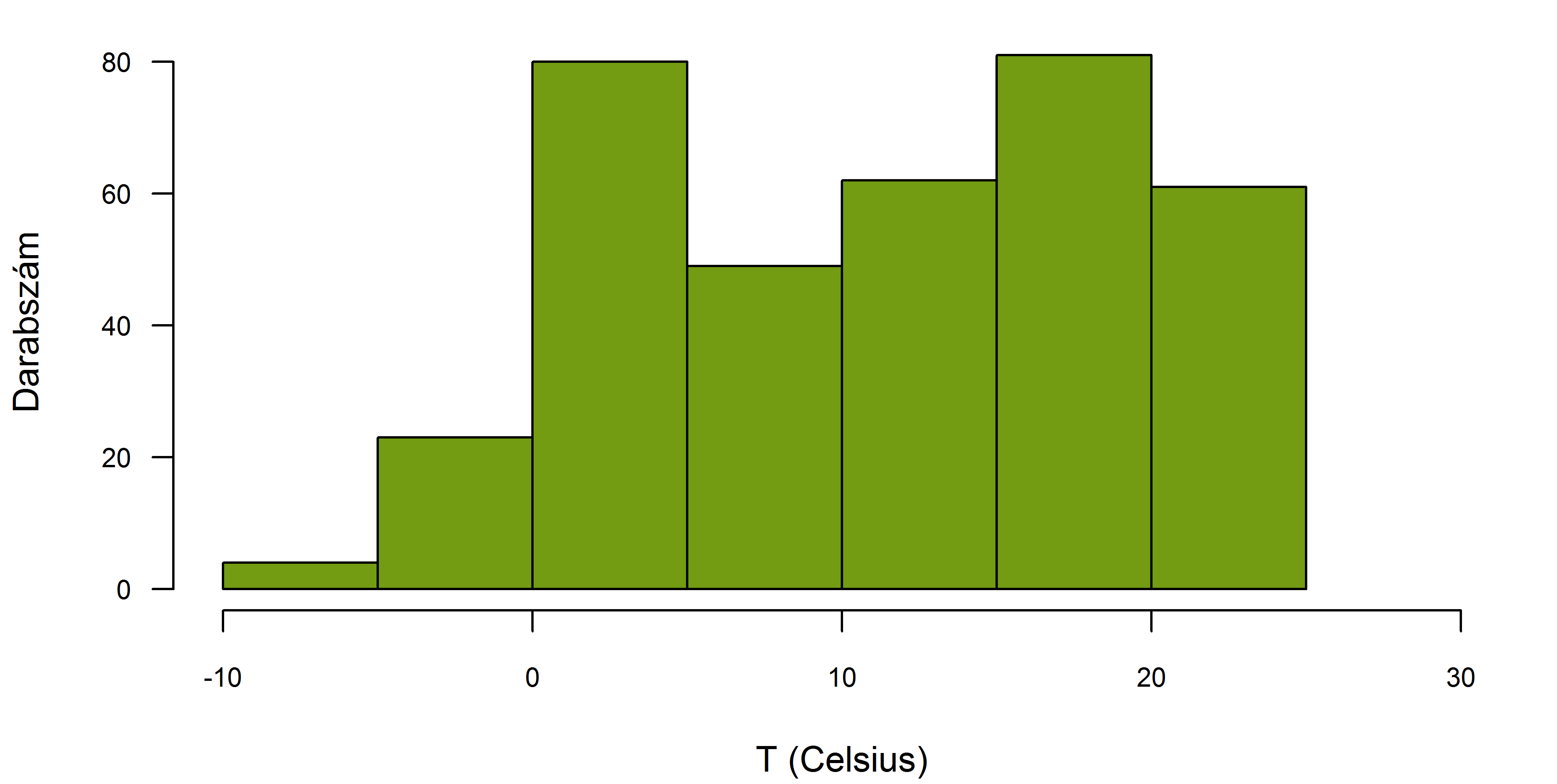
A következő 3. táblázat, 3. ábra, 4. ábra és 5. ábra mutatják Budapest környékére vonatkozóan a hőmérséklet eloszlásokat a havi hőmérsékleti adatok alapján a múlt, a jelen és a jövő vizsgált 30 éves periódusaira vonatkozóan. A méretezéshez szükséges pályaszerkezet mélységet megadva, havi szinten a pályaszerkezet hőmérsékletét és annak eloszlásait is számíthatjuk.
| Kategória | Múlt | Jelen | Jövő | |||
| [Celsius] | Darab | Gyakoriság | Darab | Gyakoriság | Darab | Gyakoriság |
| -10-(-5) | 4 | 0,0111 | – | – | 1 | 0,0028 |
| -5-0 | 23 | 0,0639 | 30 | 0,0833 | 23 | 0,0638 |
| 0-5 | 80 | 0,2222 | 68 | 0,1889 | 72 | 0,2000 |
| 5-10 | 49 | 0,1361 | 56 | 0,1556 | 54 | 0,1500 |
| 10-15 | 62 | 0,1722 | 57 | 0,1583 | 52 | 0,1444 |
| 15-20 | 81 | 0,2250 | 71 | 0,1972 | 74 | 0,2056 |
| 20-25 | 61 | 0,1694 | 77 | 0,2139 | 79 | 0,2194 |
| 25-30 | – | – | 1 | 0,0028 | 5 | 0,0139 |
 |
 |
 |
Az ekvivalens hőmérsékletek számítása, az egész országra területi átlagként érvényesen, az 1981-2010-es periódust figyelembe vevő havi hőmérsékleti idősor alapján történt. Az egész országra érvényes hőmérsékleti eloszlást 5 fokos osztásközökben a 4. táblázat tartalmazza.
| Kategória | Jelen (1981-2010) | |
| [°C] | Darab | Gyakoriság |
| -10-(-5) | 1 | 0,0028 |
| -5-0 | 39 | 0,1083 |
| 0-5 | 65 | 0,1806 |
| 5-10 | 52 | 0,1444 |
| 10-15 | 60 | 0,1667 |
| 15-20 | 81 | 0,2250 |
| 20-25 | 62 | 0,1722 |
| 25-30 | – | – |
Összefoglalás
A környezeti jellemzők alaposabb vizsgálata az alsóbbrendű vagy mezőgazdasági utaknál, az erdők feltáróhálózatánál, valamint az agro-erdészeti rendszerek kiszolgáló útjainál kifejezetten fontos, mivel ezeknél az úthálózatoknál az időjárásnak való kitettség a vékonyabb pályaszerkezet miatt erőteljesebben is érezteti hatását. Pethő (2008) mérései azt mutatták, hogy konkrétan a szélsőségesen alacsony és magas hőmérsékletek fordulnak elő gyakrabban, mint a magasabb terhelési kategóriák (vastagabb pályaszerkezetek) esetén. Az aszfalt rétegek hőmérséklet változásai lényegesek, mert az aszfaltkeverékek modulusai nagyon érzékenyek a hőmérsékletváltozásra.
Az aszfalt merevségi modulust a tényleges, reálisan várható aszfalthőmérséklet alapján célszerű felvenni, de ezen mérések csak korlátozott számban állnak rendelkezésre, szemben a léghőmérséklet mérésekkel, melyek igen jól lefedik az országot, és felhasználhatóak az aszfalthőmérsékletek – elsősorban szezonális, havi gyakoriságú – becslésére.
A cikk a léghőmérsékletnek, az aszfalthőmérsékletekkel való összefüggését, és a levonható következtetéseket dolgozta fel.
Köszönetnyilvánítás:
A publikáció megírását az EFOP 362-16-2017-00018 „Termeljünk együtt a természettel – Az agrárerdészet, mint új kitörési lehetőség” pályázat támogatta.
Irodalomjegyzék
AASHTO (1993): AASHTO Guide for Design of Pavement Structures -1993: American Association of State Highway and Transportation Officials, Washington, D. C. ISBN 1-56051-055-2, p. 624.
Asphalt Institute 1982: Research and Development of the Asphalt Institute’s Thickness Design manual (MS-1), 9th ed. Research Report 82-2, Asphalt Institute, Lexington, KY
Claessen, A. I. M., Edwards, J.M., Sommer, P. & Ugé, P. 1977: Asphalt Pavement Design, The Shell Method, 4th International Conferenceon Design of Asphalt Pavements, 1977, pp. 39-65.
Diefender, B. K.,Al-Qadi, I. L. & Diefender, S. D. 2006: Model to predict Pavement Temperature Profile: Development and Validation. Journal of Transportation Engineering, ASCE, 132(2): 162-167, https://doi.org/10.1061/(ASCE)0733-947X(2006)132:2(162)
Dingman, L., S. 2002: Physical Hydrology. Prentice-Hall. ISBN: 0-13-099695-5, p. 646.
Drumm, E. C. & Meier, R. 2003: LTPP Data Analysis: Daily and Seasonal variations in Insitu Material Properties, 2003 NCHRP Web Document 60.
Fernando, E. G.,Liu, W. & Ryu, D. 2001: Development of a procedure for temperature correction of back calculated AC modulus. Report 1861-1. Texas Transportation Institute, Texas AM University System. p. 147.
French Desing Manual for Pavement Structures. Guide technique. Laboratoire Central Ponts et Chaussées (LCPC), Secvice d’EtudesTechniques des Routes et Autoroutes (SETRA) Centre de la Sécurité et des Techniques Routiéres, May 1997.
George, K.P. & Husain, S. 1986: Thickness design for flexible pavement: a probabilistic approach, Transportation Research Record, Vol.1095, pp 26-36.
Gupta, A. 2014: A review of Environmental Factors on Flexible Pavement Modelling, Modern Traffic and Transportation Engineering Research, vol:3 iss:1 pg:14-20
Pethő, L. 2008: A hőmérséklet eloszlás alakulása az aszfalt burkolatú pályaszerkezetekben és ennek hatása a pályaszerkezeti rétegek méretezésére, technológiai tervezésére. PhD értekezés. Budapesti Műszaki és Gazdaságtudományi Egyetem.
Stubstad, R. N., Lukanen, E. O., Richter, C. A. & Baltzer, S. 1998: Calculation of AC Layer Temperatures from FWD Field Data. in: Proc. of the 5th International Conference on the Bearing Capacity of Roads and Airfields, Trondheim, Norway, p. 919-928.
Ureczky, J., & Tóth, Cs. 2008: A hőmérséklet teherbírásra gyakorolt hatásának vizsgálata. Közúti és mélyépítési szemle., 2008 április, 3. szám. 9-14.
Ullidtz, P. 1998: Modelling Flexible Pavement Response and Performance. TechUniv. of Denmark Polyteknisk, ISBN: 978-8750208051, p. 205.
Witczak, M. W. 1972: Design of full-depth asphalt airfield pavements, Proceedings of the 3rd International Conference on the Structural Design of Asphalt Pavements: 550-567.
Zapata, C. 2018: Empirical approach for the use of unsaturated soil mechanics in pavement design. Geotechnical Special Publication, 2017-November (GSP 300), 149-173. https://doi.org/10.1061/9780784481677.008
Erre a szövegre így hivatkozhat:
Herceg András, Primusz Péter, Kalicz Péter, Gribovszki Zoltán: A klimatikus jellemzők hatásai az útpályaszerkezetre: A pályaszerkezet hőmérsékletek számítása, Útügyi Lapok, 2020, DOI: 10.36246/UL.2020.2.02
