Pdf: A járműsebesség hatása a pályaszerkezetek élettartamára
Bevezetés
Pályaszerkezeteink teherhordó szerkezetek, igénybevételeiket a járműforgalomból és a meteorológiai hatásokból kapják.
A járműforgalom hatása azonban korántsem mennyiségi kérdés, számít többek között a járműsebesség is.
Jelen írásnak a célja a járműsebességből eredő hatások számszerűsítése, egy konkrét nagy forgalmú autópálya szakasz esetében.
Ez egyben egy másik, fontos kérdés része, mit tudunk megállapítani meglévő aszfaltszerkezeteink méretezési tulajdonságairól, de erről csak a végén.
Elméleti alapok
Sajnálatos módon a probléma értelmezéséhez szükségesek némi elméleti alapok is, ezeket itt foglalom össze.
Az aszfalt merevségének terhelési idő (sebesség) függése
Útpályaszerkezeteink aszfaltja viszkózus tulajdonságokkal (is) rendelkezik, ez-egyebek között – az aszfaltok merevségének terhelési idő függésében nyilvánul meg, 1. ábra.
 |
Jól megfigyelhetők a következők:
• a terhelési idő függés a viszkózus tulajdonságok „hordozójától” a kötőanyagtól függ
• egy viszonylag alacsony járműsebességtől kezdve a függés gyakorlatilag lineáris (ezt jeleztem pontozott vonallal)
• a merevség a haladási sebesség csökkenésével lényegében arányosan csökken, a kisebb merevség nyilvánvalóan az alacsonyabb élettartam irányába hat
Haladási sebesség, terhelési idő, frekvencia
A terhelési idő, a haladási sebesség és a terhelési frekvencia között képletszerű összefüggés van, amit a 2. ábrán láthatunk.
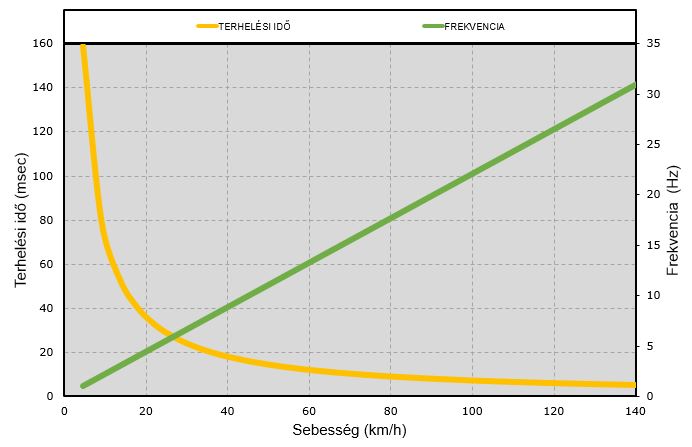 |
Pályaszerkezet élettartam
A pályaszerkezet élettartamát – egyszerűsítve – azonosnak veszem az aszfaltszerkezet alsó szálában keletkező megnyúlásból meghatározhatóval, megjegyzem, ennél lényegesen komplexebb élettartam kritérium is figyelembe vehető.
Aszfaltnyúlás számítása
A meglévő pályaszerkezetekben keletkező megnyúlások meghatározására számos eljárást dolgoztak ki, alapvetően az FWD technológia elterjedésének hatására.
(Van Gurp, 1997) számos regressziót fejlesztett a konkrét probléma megoldására, köztük két nagyon gyakorlatias és egyszerű megoldást, amit a továbbiakban alkalmazni fogunk, ezért részletesebben ismertetjük.
Az aszfaltszerkezet alsó szálában keletkező megnyúlást – 150 mm – nél vastagabb aszfaltszerkezetek esetében – a következő képlettel lehet meghatározni:
\[LOG_{(10)\epsilon}=0,481+0,881*LOG_{(10)}SCI\]
| ahol: | |
| \(\epsilon\) | a keletkező aszfaltnyúlás, microstrain |
| \(SCI\) | a központi és a 300 mm távolságban mért behajlás különbsége, microméter |
Az aszfaltszerkezet felső szálában az összefüggést Van Gurp a következők szerint állapította meg:
\[\epsilon_{b}=194,895-20,7769*SCI^{0,5}\]
| ahol: | |
| \(\epsilon_{b}\) | a burkolatfelületen keletkező aszfaltnyúlás, microstrain |
| \(SCI\) | a központi és a 300 mm távolságban mért behajlás különbsége, microméter |
A kétféle megnyúlásértek kapcsolatát az SCI értékkel a 3. ábra mutatja.
 |
Jól megfigyelhető, hogy az SCI növekedésére (a központi terheléshez illeszthető görbületi sugár csökkenésére) az aszfaltréteg alsó szálában nő a megnyúlás, a felső szálban csökken.
SCI érték frekvenciafüggése
Az SCI értékekből, mint látjuk, lehetséges számítani az aszfaltnyúlásokat.
Nyilvánvaló, hogy mivel az aszfaltrétegek merevsége függ a terhelési időtől, a pályaszerkezeten mérhető/számítható SCI értéknek is kell, hogy kapcsolata legyen ezzel, 4. ábra.
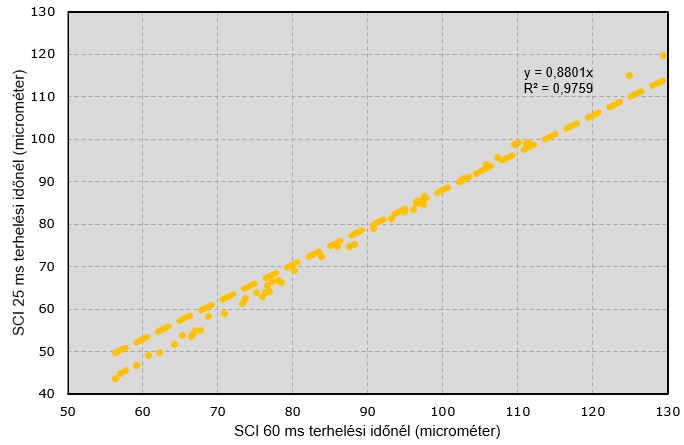 |
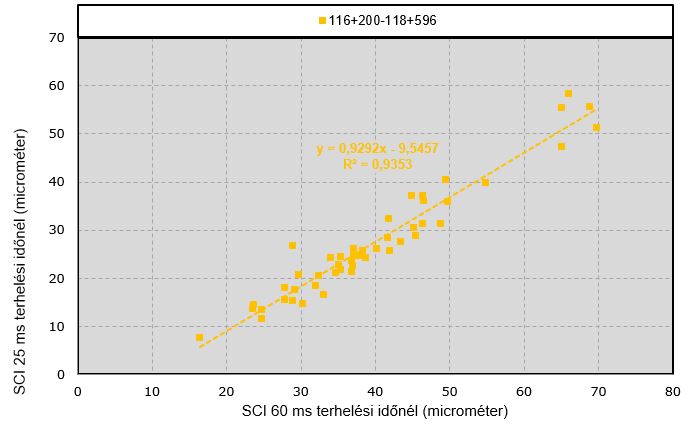
(Van Gurp, 1995) – ez egy nyughatatlan holland mérnök, mindig csinál valamilyen érdekes dolgot – regressziós összefüggést fejlesztett ki a KUAB típusú ejtősúlyos behajlásmérők esetére.
Az összefüggés a 25 ms terhelési idő alatti behajlási teknőparaméterek meghatározására vonatkozik a 60 ms (normál) KUAB terhelési időből kiindulva.
A regressziós összefüggés alapszerkezete a következő:
\[d25_{i}=a_{i}+b_{i}*d60_{0}+c_{i}*d60_{300}+d_{i}*d60_{600}+e_{i}*d60_{900}+f_{i}*d60_{1200}\]
| ahol: | |
| \(d25_{i}\) | lehajlás az FWD-től i mm távolságra, 25 ms terhelési impulzus mellett, microméter |
| \(d60_{i}\) | lehajlás az FWD-től i mm távolságra, 60 ms terhelési impulzus mellett, microméter |
| \(a_{i} – f_{i}\) | regressziós tényezők a következő táblázat szerint |
| Távolság, mm | ai | bi | ci | di | ei | fi |
|---|---|---|---|---|---|---|
| 0 | 20,544 | 1,08 | -0,631 | |||
| 300 | 27,268 | 1,153 | -0,675 | |||
| 600 | 22,021 | -0,39 | 1,205 | -0,223 | ||
| 900 | 2,605 | 0,64 | ||||
| 1200 | 4,697 | 0,644 | ||||
| 1500 | 4,468 | 0,627 | ||||
| 1800 | 6,794 | -0,35 | 1,133 | -1,323 | 1,161 |
A kapcsolatot egy méréssor alapján a 4. ábrán mutatom be.
A halmozott károsodások törvénye
Útpályaszerkezeteink a forgalomból és a környezeti hatásokból (ezek főleg meteorológiai jellegűek) eredő igénybevételek hatására fokozatosan, fáradási tönkremenetelt szenvednek el.
Ez a tapasztalt tönkremeneteli formák nagyon nagy részénél (repedések alulról felfelé, repedések felülről lefelé, keréknyomképződések különböző formái) mind igaz, legfeljebb az egyes tönkremeneteleket előidéző ismétlésszám különbözik jelentősen.
A pályaszerkezettel foglalkozó mérnök számára a problémát az jelenti, hogy a forgalomból és a környezetből keletkező igénybevételek nagyságai jelentősen különböznek.
A különböző nagyságú (vagy különböző feltételek mellett ható) igénybevételek összesített károsító hatásának számítására a Palmgren – Miner nevéhez fűződő összefüggés használata általános.
Az összefüggés a következők szerint írható le:
\[\frac{n_{1}}{N_{1}}+…+\frac{n_{i}}{N_{i}}+…+\frac{n_{n}}{N_{n}}=x\]
| ahol: | |
| \(n_{i}\) | az adott terhelési szinthez tartozó tényleges teher-ismétlésszám |
| \(N_{i}\) | az adott terhelési szinthez tartozó, tönkremenetelt okozó teher-ismétlésszám |
| \(x\) | a tönkremenetel valószínűsége |
Az esettanulmány
Bizonyos, alább ismertetett események miatt egy gyorsforgalmú útszakasz kezelője kíváncsi lett a járműsebesség változásának az élettartamra gyakorolt hatására.
A szabályozás és következményei
A gyorsforgalmi utakra 2010 – ben új szabályozás jelent meg, lényege az alábbiakban olvasható:
„(6) Tilos előzni az azonos irányú forgalom számára két forgalmi sávval rendelkező autópályán és autóúton – 6 és 22 óra között – a 7500 kg-ot meghaladó megengedett legnagyobb össztömegű tehergépkocsival, vontatóval, valamint e járműből és pótkocsiból álló járműszerelvénnyel.
(7) A (6) bekezdésben meghatározott előzési tilalom esetén a tilalom hatálya alá tartozó járműveknek olyan követési távolságot kell tartaniuk, hogy közéjük legalább egy – az abban meghatározott előzési tilalom hatálya alá tartozó – járműszerelvény biztonságosan besorolhasson.”
Tapasztalatok
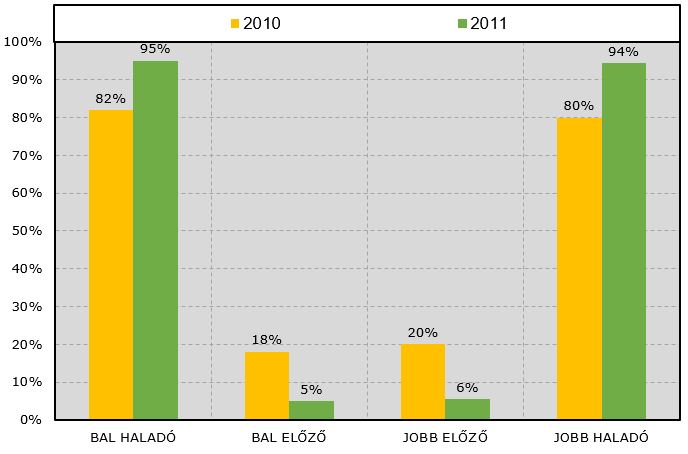
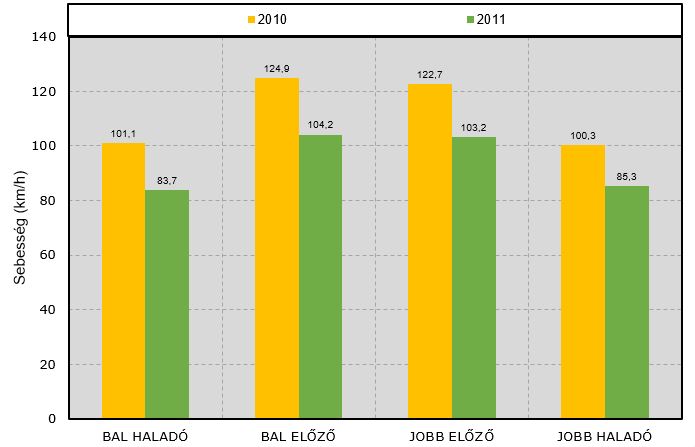
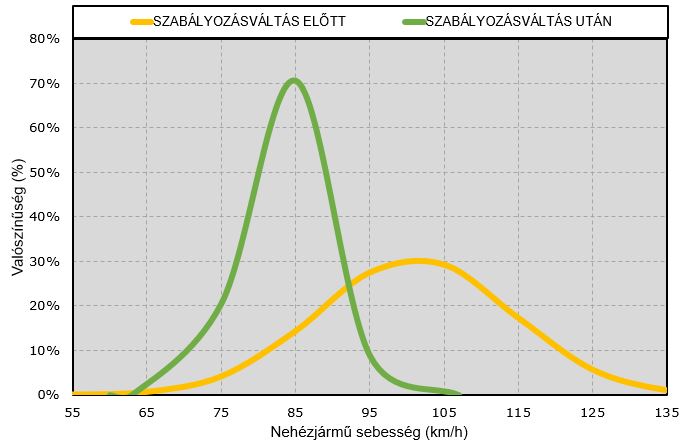
A szakaszon rendelkezésre álltak járműszám és sebességmérési adatok, kiválasztottunk két azonos hosszúságú időperiódust (2010 illetve 2011 évekből) és megvizsgáltuk a nehéz járművek forgalmi sávok közötti eloszlását és az átlagsebességek alakulását a szabályozásváltozás előtt és után, ennek a vizsgálatnak az eredményét az 5-7. ábrákon láthatjuk.
A következő megállapítások tehetők:
a) az alapvetően forgalombiztonsági okok miatt keletkezett szabályt betartják
b) a nehéz forgalom gyakorlatilag teljesen a haladósávra került
c) a járműsebességek nagymértékben csökkentek, az átlagsebesség több, mint 10 % – al.
 |
 |
 |
A kiválasztott szakasz merevségének sebességfüggése
A tényleges vizsgálat egy hosszabb szakaszra terjedt ki, amelyet – statisztikai módszerekkel – a merevségfüggés szempontjából homogén alszakaszokra bontottam.
A továbbiakban ezen alszakasz eredményeit ismertetem, 8-9. ábra.
 |
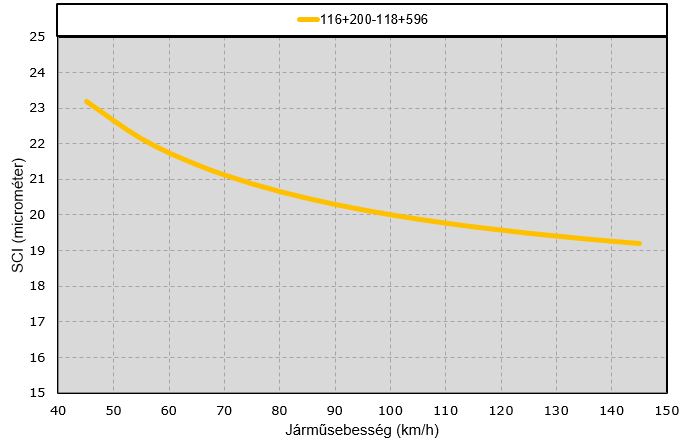 |
A 8. ábrán az ejtősúlyos behajlásmérés eredményeiből számított terhelési idő függés látható, ebből számoltam az SCI teknőparaméter sebességfüggését a vizsgált szakaszra.
A halmozott károsodások számítása
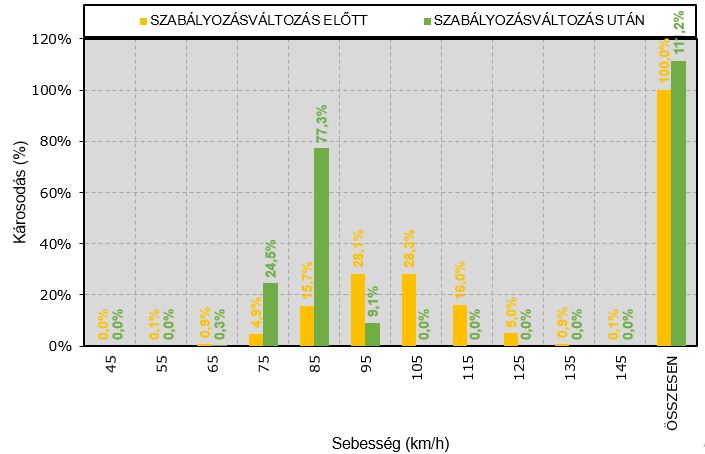
A már ismertetett Palmgren – Miner törvény alapján végrehajtottam a sebességeloszlás megfelelően választott osztályközeiben az egyedi károsodások számítását, a szabályozás előtti és utáni sebességek esetére.
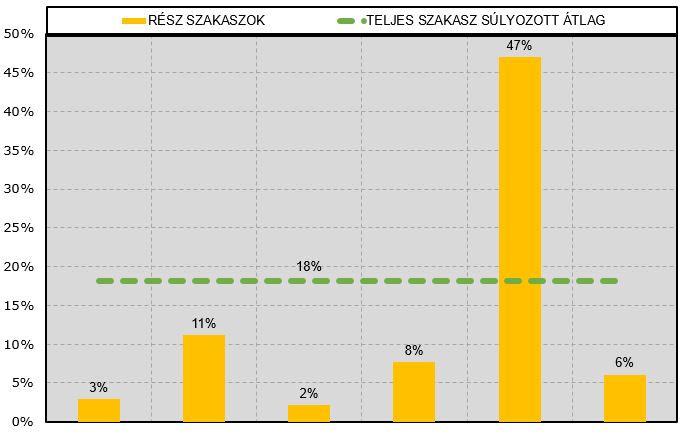
A számításnál a szabályozás előtti állapotot vettem 100% – nak, hogy az összehasonlítás plasztikus legyen, 10. ábra.
 |
Megvizsgálva az eredményt, a következő megállapítások tehetők:
• a kisebb sebességek kb. 11% – al nagyobb károsodást, következésképpen ennyivel rövidebb élettartamot jelentenek.
• a károsodásnövekedés az összes szakaszon tapasztalható volt, mértéke eltérő, ezt megvizsgálhatjuk a következő diagramon
• mindenképpen meg kell jegyezni, hogy a megengedett megnyúlás értéket – egyéb forrásokra támaszkodva, egy mérnöki becsléssel, de azonosnak tételeztem fel
• miután adott esetben a csökkenés kritikus is lehet, adott esetben célszerű további vizsgálatok végrehajtása is, ezek a frekvenciafüggés és a szintén megállapítható hőmérsékletfüggés ismeretében (kvázi ismerjük a mestergörbét) a tényleges fáradási tulajdonság meghatározására irányulhat
• ez utóbbi számítás elvégzése lehetséges, én két olyan komplex kutatást is ismerek (Medani, 2006), (Jacobs 1995) amelyek alapján végrehajtható, hangsúlyozottan aszfaltmechanikai vizsgálatok nélkül
 |
Összefoglalás
Ezzel a kissé hosszabbra sikerült írással azt kívántam érzékeltetni, hogy a pályaszerkezetek világa ugyan elég komplex, de igazából némi szorgalommal a komplex problémák is megoldhatók.
Irodalomjegyzék
Van Gurp. C.A.P.M.; Wennink, P.M. : Design, structural evaluation an overlay design of rural roads (in Dutch) KOAC – WMD consultans; Apeldoorn, 1997
Christ van Gurp,Characterization of seasonal influences on asphalt pavements with the use of falling weigh deflectometers PHD disszertáció, Delft 1995
Tarig Obeid Medani; Design Principles of Surfacings on Orthotropic Steel Bridge Decks PHD disszertáció, Delft 2006
Mathias Maria Johannes Jacobs; Crack Growth in Asphaltic Mixes, PHD disszertáció, Delft 1995
