https://doi.org/10.36246/UL.2020.2.04
2020; 8. évfolyam, 14. szám
Pdf: A gumiabroncs és az útpályaszerkezet érintkezési kapcsolatának elemzése végeselem módszerrel
Bevezetés
A mechanikai-empirikus útpályaszerkezet méretezési rendszerek a pályaszerkezetet rugalmasságtani elven számítható szerkezetként fogják fel, és alapvetően a vékony lemezek vagy a rugalmas rétegek elméletét alkalmazzák (McCullough és Boedecker, 1969). Bármilyen méretezési eljárást is alkalmazzunk, annak előfeltétele, hogy ismerjük az útburkolatra ható erőket, vagyis azt a felületet, amin a terhelés a szerkezetre átadódik. Kezdetben a Boussinesq-féle egyenleteken alapuló módszerek feltételezték, hogy az erő koncentráltan vagy vonalmenti eloszlásban működik a kerék teljes szélességén (Kézdi, 1954). A pneumatikus kerekek elterjedésével már azt gondolták, hogy a terhelés olyan körlakú érintkezési felületen adódik át, amin a keréksúly egyenletesen oszlik meg. Ez a feltevés sokáig megmaradt, mivel egyszerű számítást tett lehetővé és a rugalmas rétegek parciális differenciálegyenleteinek megoldása is csak erre a terhelési esetre létezett.
Az elméleti megközelítéseket később a probléma kísérleti megoldása egészítette ki: különböző terhelésű kerekeket papírlapok közé helyezett festékes fóliára ráengedve (Kézdi, 1954), vagy azok homok körbeszórásával (Zsichla, 1990), a gumiabroncsok lenyomata meghatározhatóvá vált. Betonburkolatok esetén a kerék és az útburkolat érintkezési felülete ellipszis alakú volt a korra jellemző diagonál abroncsoknál, nagyságát pedig a belső tömlőnyomás és a kerékterhelés határozta meg. A jóval később megjelenő és merevebb radiálabroncsok keresztirányban nem, csak hosszirányban képesek alakváltozást elszenvedni, így lenyomatuk képe inkább téglalapra hasonlított (Gent és Walter, 2006). A kísérleti eredmények ellenére a legtöbb méretezési eljárás – a számítási nehézségekből adódóan – a tehergépkocsi ikerabroncs két ellipszis vagy inkább téglalap alakú lenyomatát a továbbiakban is egy azokkal megegyező nagyságú helyettesítő körfelülettel vette figyelembe. Ezt a megközelítést alkalmazta Nemesdy (1992) is a magyar új építésű típus-útpályaszerkezet katalógusrendszer megalkotásakor. Szakmai körökben viszont újra és újra felerősödtek azok a kritikus hangok, akik ezt az egyszerűsítést nem tartották elfogadhatónak. A számítástechnika fejlődésével ugyanis lehetőség nyílt arra, hogy a szuperpozíció elvét felhasználva a köralakú terhelési esetre levezett egyenletekkel már kerékelrendezéseket is modellezzünk. Erre mutat példát Adorjányi (2009) aki a 2×25 kN nagyságú ikerabroncs terhelést két egymástól 315 mm-re elhelyezett 210 mm átmérőjű körfelületen egyenletesen megoszló erőrendszerrel veszi számításba. Szokás szerint a megoszló erőrendszer nagyságát, vagyis a felületi nyomást – jó közelítéssel – a gumiabroncsok belső légnyomásával megegyezőnek tételezzük fel. Ezt a gyakorlatot csak nagyon ritkán kérdőjelezzük meg, pedig az érintkezési lenyomatnál sokkal jobban meghatározza a szerkezetben ébredő igénybevételeket.
Cikkünkben a modern gumiabroncsok és az útpályaszerkezetek interakcióját vizsgáljuk a végeselem módszerrel, mivel egy komplex abroncsmodell felépítéséhez nem csak sok anyagparaméterre, de egy triviálisnak nem mondható modellezési technikára is szükségünk van, amellyel a különböző anyagú rétegek egymásra épülő rendszere jól leírható a lehető legkevesebb végeselemszámmal. Nagy gyártók, mint pl. a Hankook, a 2000-es évek elején kezdték a manapság használatosnak mondható modellezési technika kifejlesztését (Kennedy, 2003), amivel ma már a legtöbb abronccsal kapcsolatos probléma jól kezelhető. Reméljük, hogy munkánkkal segíteni tudjuk tisztázni a bevezetőben feltárt vitás kérdéseknek egy részét.
Elméleti háttér
A gumiabroncs nyomásviszonyai
A gépjárművek a kerekeiken keresztül támaszkódnak fel az úttestre. A kerékterhelést pedig a gumiabroncsok adják át az útpályaszerkezetnek. Feltevésünk szerint a járműterhelésből adódó nyomóerő egyenletesen megoszlik a gumiabroncs A felfekvési felületén (1.a ábra):
\[p=\frac{F}{A} \]
ahol a gumiabroncs belső légnyomása, ami közel azonosnak tekinthető a gumiabroncs által a burkolatnak átadott fajlagos érintkezési nyomásával. Szigorúan véve a egyenlőség csak tökéletesen hajlékony, vagyis saját merevséggel nem rendelkező keréktömlő esetén igaz. Abban az esetben, ha a gumiabroncsnak van saját merevsége, akkor a kontaktfeszültség akár 10-30 százalékkel lehet nagyobb vagy akár kisebb, mint az abroncs belső légnyomása a korabeli szakirodalom szerint (Kézdi, 1954; Lawton, 1957; Yoder, 1959; Lister és Nunn, 1968).
 |
Az ellentmondásos eredményekre Van Vuuren (1974) munkája adott később magyarázatot, aki fizikai levezetéssel igazolta, hogy egy léggömb q fajlagos érintkezési nyomása miért szükségszerűen kisebb, mint annak belső p légnyomása (1.b ábra):
\[q=p-\frac{4T}{D}sinΘ + \frac{F’}{A} \]
| ahol: | |
| \(q\) | átlagos kontakt nyomás |
| \(T\) | húzóerő / egységhossz (a kontakt felület peremén) |
| \(Θ\) | a húzóerő és a vízszintes által bezárt szög |
| \(A\) | kontakt körfelület |
| \(D\) | kontakt körfelület átmérője |
| \(F’\) | a léggömb fala által közvetített terhelés |
Mivel a T húzóerő a belső p légnyomásnak és a külső F erőnek egyaránt függvénye, így a keresett átlagos q kontaktnyomás is p és F függvényének tekinthető, vagyis általánosságban a következő összefüggés fogalmazható meg:
\[q=f_{1}(p)+f_{2}(F, p) \]
| ahol: | |
| \(f_{1}(p)\) | a belső légnyomás függvénye, és |
| \(f_{2}(F, p)\) | a belső légnyomásnak és a külső terhelésnek az együttes függvénye (hatása). |
Van Vuuren (1974) a léggömbre levezetett (3) összefüggést kiterjesztette gumiabroncsokra is, ahol az abroncs fizikai felépítését, méreteit, a futófelület kialakítását, a gumi keménységet és falvastagságot egy C’ tényezővel vette számításba:
\[q=f_{1}(p)+f_{2}(F, p)+C’ \]
A levezett (4) összefüggést Van Vuuren (1974) laboratórium mérésekkel igazolta egy 8.25-20×10 típusú gumiabroncsra:
\[q=(0,013p+10,5)F+0,119p+125,9 \]
ahol q és p kPa-ban, az F kerékterhelés pedig kN-ban értendő. Az (5) tapasztalati összefüggés szerint az érintkezési (kontakt) nyomás a kerékterheléstől, az abroncs belső légnyomásától és nagymértékben az abroncs „hajlékonyságára” jellemző C’ konstans értékétől függ.
A gumiabroncs felépítése
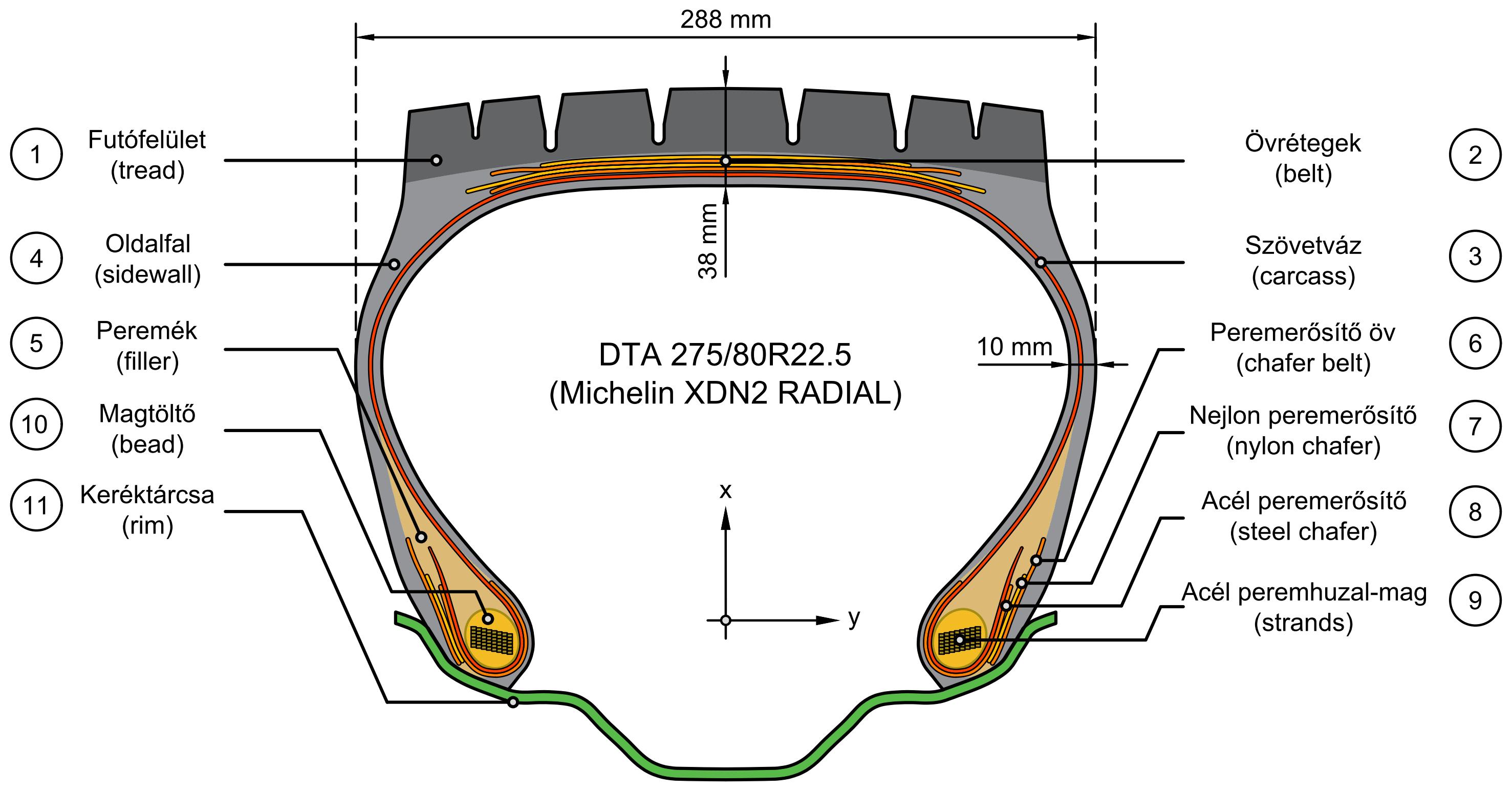
A gumiabroncsok a külső szemlélő számára egyszerű felépítésűnek tűnnek, pedig a modern abroncsok nagyságrendileg 10-20 különböző alkatrészt tartalmaznak, amik együttesen adják a gumiabroncsoktól megkívánt műszaki tulajdonságokat. A modern abroncsok legfontosabb részei a következőek (a 2. ábra szerint számozva):
- A futófelület (tread) az abroncs útfelülettel érintkező része, feladata biztosítani a tapadást, a kopásállóságot és a menetstabilitást a járműnek (1). Jellemzően szintetikus és természetes kaucsukból készül.
- Az övrétegek (belt) erősítik az abroncsot, elnyelik az ütéseket, az optimális menetstabilitást és gördülési ellenállást biztosítják a járműnek (2). Gumírozott nagyszilárdságú acélszálakból készülnek, a szálak helyzete a radiál abroncs felhasználási céljának és terhelhetőségének függvényében ±10-30° a középvonalhoz képest.
- A szövetváz (carcass) az abroncs vázát adja, magas légnyomások esetén is megőrzi a gumiabroncs alakját és elosztja a terhelést (3). Gumírozott rayon vagy poliészter textilszálakból készül.
- Az oldalfal (sidewall) természetes gumiból készül, védi a karkaszt az oldalirányú behatásoktól és átviszi a nyomatékot a futófelületre (4).
- A peremék (filler) elősegíti a menetstabilitást, a kormányzási és kényelmi adottságokat, szintetikus gumiból készül (5).
- A peremerősítő öv (chafer belt) fokozza a menetstabilitást és a kormányzás pontosságát (6), anyaga lehet acél vagy nejlon, így megkülönböztettünk nejlon (7) és acél (8) peremerősítőt.
- Az acél peremhuzal-mag vagy huzalkarika (strands) gumiba ágyazott nagyszilárdságú acélhuzalokból készül, ami stabil illeszkedést biztosít a gumiabroncs és a keréktárcsa között (9). Az alkalmazott gyártástechnológiától függően a huzalkarika lehet magtöltős (bead) vagy magtöltő nélküli (10).
A gumiabroncs legbelső rétege légzáró, feladata, hogy megtartsa a gumiabroncsba fújt levegőt, valamint megakadályozza a pára és nedvesség bejutását.
A végeselem módszer
A végeselem módszer (VEM) egy numerikus eljárás a természettudományok és a műszaki élet feladatainak közelítő megoldására. Lényege, hogy a vizsgált tetszőleges geometriai kialakítású, tetszőleges peremfeltételű és tetszőleges terhelésfeltételekkel rendelkező testet véges számú, kicsiny, de geometriailag jól meghatározott ún. véges elemekből felépített modellel helyettesítjük (Molnár, 2011).
 |
Ezek a végeselemek csak a csomópontjaikban kapcsolódnak egymással. A csomópontok elmozdulása (ue) és a csomópontokban ható erők (Fe) közötti kapcsolatot a végeselemek viselkedését leíró törvényszerűségek, anyagmodellek (Ke az elem ún. merevségi mátrixa) határozzák meg (Kakucs, 2020):
\[F^{e}=K^{e}u^{e} \]
Az összekapcsolódó végeselemek együttes viselkedését egy egyenletrendszer írja le, amelynek megoldása a vizsgált tárgy alakváltozási állapotát adja. A csomópontok egymáshoz viszonyított relatív elmozdulása a végeselemek torzulásához vezet, amiből a fellépő feszültségek a már említett törvényszerűségekkel kiszámíthatók (Kakucs, 2020).
A végeselemes módszer kézi számításokra alkalmatlan, mivel nagyon sok elemi művelet elvégzését igényli már egy igen egyszerű feladat is. Ezért ma már mindenhol számítógépes programokat használnak, hogy az iparban is fontos feladatok megoldhatóak legyenek. Az egyik legelterjedtebb végeselem szoftver jelenleg az ABAQUS/CAE (Complete Abaqus Environment) ami hatékony és komplett megoldást jelent az ipari feladatok széles spektrumához. A program implicit és explicit mechanikai, áramlástani és elektromágneses megoldóval rendelkezik, de SPH (Smoothed Particle Hydrodynamics), DEM (Discrete Element Method) és többtest dinamikai problémákat is megoldhatunk vele (Tamás et al. 2014). Fontos alprogramja a TOSCA, ami geometria vagy paraméter optimalizálásra használatos.
Anyagmodellek
A modern gumiabroncsok felépítésükből következően többféle alapanyagból készülnek, és ezeknek csak egy kis részére igaz, hogy a lineárisan rugalmas (Hooke) anyagmodellt követik. A gumira például a nagyon nagy és nem lineáris deformációk jellemzők. Ezt az anyagviselkedést az ún. hiper-viszkoelasztikus anyagmodellel írhatjuk le, ami egy hiperelasztikus és egy viszkoelasztikus modell összekapcsolásán alapszik (Fazekas és Goda, 2017). Előbbi az anyag időfüggetlen, utóbbi az időfüggő viselkedést jellemzi (Brinson és Brinson, 2015). A mérnöki gyakorlatban a hiper-viszkoelasztikus modellparaméterek meghatározása nem egyértelmű feladat, ezért inkább a szeparált illesztés terjedt el (Fazekas és Goda, 2017). Ez azt jelenti, hogy a hiperelasztikus és a viszkoelasztikus paramétereket külön-külön illesszük a mérésekre, ez viszont pontatlanabb eredményeket ad a direkt módszerhez képest.
A hiperelasztikus anyagmodellben a feszültség és a nyúlás közötti kapcsolatot az alakváltozási energia sűrűségfüggvény írja le. Több általános hiperelasztikus konstitutív törvény ismert, mint pl. a Neo-Hooke, a Mooney-Rivlin, a Yeoh és az Ogden. A Yeoh modell az első deformációs invariánson alapszik, és a háromparaméteres változata jó illeszkedést biztosít a nagy deformációk tartományában (Madocsai, Veress, és Palkovics, 2011):
\[ W= C_{10}(ī_{1}-3)+C_{20}(ī_{1}-3)^{2}+C_{30}(ī_{1}-3)^{3}+\frac{1}{D_{1}}(J_{el}-1)^{2} +\frac{1}{D_{2}}(J_{el}-1)^{4}+\frac{1}{D_{3}}(J_{el}-1)^{6} \]
| ahol: | |
| \(C_{i0}\) | anyagparaméterek [Pa] |
| \(ī_{1}\) | deformációs invariáns |
| \(D_{i}\) | összenyomhatatlansági paraméterek [1/Pa] |
| \(J_{el}\) | elasztikus térfogati állandó |
Az anyag időfüggő (t) viszkoelasztikus viselkedése Prony-sorozattal közelíthető az alábbi formában:
\[ g_{r}(t)=1-∑g_{i}(1-e^{\frac{-t}{τ_{1}}}) \]
ahol N a viszkoelasztikus modell elemeinek száma, \( τ_{1} \) az i-edik relaxációs idő, míg \( g_{i} \) az i-edik relatív csúsztató rugalmassági modulus. A dimenziótlan \( g_{r}(t) \) relaxációsmodulus-függvény az időfüggő G(τ) és a pillanatnyi (üveges) \( G_{0} \) csúsztató modulus hányadosaként van értelmezve:
\[ g_{r}(t)=G(t)/G_{0} \]
A most bemutatott anyagmodellekről további részleteket olvashatunk Tamás és mtsai. (2014) szabadon elérhető oktatási anyagában.
Anyagok és módszerek
Gumiabroncs és útpályaszerkezet adatok
A mechanikai alapú útpályaszerkezet méretezés alapvetően Burmister (1945a; 1945b; 1945c) elméletét felhasználva a lineárisan rugalmas, homogén és izotróp végtelen féltéren nyugvó, többrétegű hajlékony rétegek rendszerével modellezi a valóságos útpályaszerkezeteket (MLE, Multilayer Elastic). A modellen belül egy h vastagságú réteg mechanikai viselkedését a Hooke-féle anyagtörvénynek megfelelően az E rugalmassági vagy Young-modulus és a μ harántkontrakciós, vagy Poisson-tényező adja meg. A rétegek a szerkezeteken belül egymáshoz tökéletesen tapadnak, vagyis a rétegek nem tudnak elcsúszni a határfelületen. A kutatásban vizsgált hajlékony és félmerev útpályaszerkezetek rétegrendjét és a rétegek mechanikai tulajdonságait az 1. táblázatban foglaltuk össze.
|
Réteg neve |
Vastagság, h [mm] |
Young-modulus, E [Mpa] |
Poisson-tényező, µ [-] |
|
A hajlékony útpályaszerkezet felépítése |
|||
| Aszfalt kopóréteg | 40 | 4000 | 0,35 |
| Aszfalt kötő- és alapréteg | 200 | 5500 | 0,35 |
| Zúzottkő alapréteg | 250 | 350 | 0,40 |
| Földmű | 20000 (végtelen) | 50 | 0,45 |
|
A félmerev útpályaszerkezet felépítése |
|||
| Aszfalt kopóréteg | 40 | 4000 | 0,35 |
| Aszfalt kötő- és alapréteg | 200 | 5500 | 0,35 |
| CKT alapréteg | 200 | 2000 | 0,40 |
| Földmű | 20000 (végtelen) | 50 | 0,45 |
|
# |
Elem |
Típus |
Anyag |
Réteg |
Szög [°] |
Kereszt-metszet |
Geom. |
Köz |
| 02 | övrétegek | erősítés | öv-acél | 1 | 50 | kör | R 0,25 | 1,16 |
| 2 | 78 | kör | R 0,25 | 1,16 | ||||
| 3 | 102 | kör | R 0,25 | 1,16 | ||||
| 4 | 78 | kör | R 0,25 | 1,16 | ||||
| 09 | huzalkarika | huzal-acél | 8×6 | 90 | hasáb | 2,0×1,3 | szoros | |
| 03 | szövetváz | szövet-acél | 1 | 12 | kör | R 0,4 | 0,8 | |
| 2 | -12 | kör | R 0,4 | 0,8 | ||||
| 06 | peremerősítő öv | peremerősítő-acél | 1 | 90 | kör | R 0,36 | 1,19 | |
| 08 | acél peremerősítő | peremerősítő-acél | 1 | 90 | kör | R 0,36 | 1,19 | |
| 07 | nejlon peremerősítő | peremerősítő-nejlon | 1 | 90 | kör | R 0,36 | 1,00 | |
| 01 | futófelület | fő szerkezet | futófelület gumi | 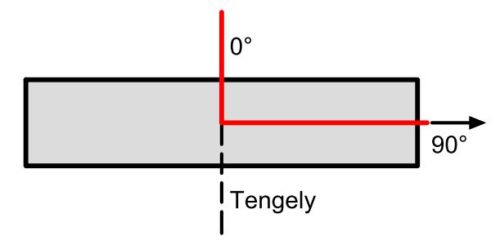 |
||||
| 04 | oldalfal | oldalfal gumi | ||||||
| 10 | magtöltő | magtöltő gumi | ||||||
| 05 | peremék | magtöltő gumi | ||||||
| 11 | keréktárcsa | görgetett acél | ||||||
 |
A gumiabroncs szerkezetének geometriáját Hernandez et al. (2017) által közölt DTA 275/80R22.5 típusú abroncs keresztmetszeti rajza alapján (21. oldal) rekonstruáltuk, az abroncsok szélessége így (overall width) 288 mm-re, az abroncsok távolsága (dual spacing) pedig 315 mm-re adódott. A 2. ábrán látható abroncs kompozit szerkezetének a geometriai méreteit a 2. táblázat (a részek számozása a 2. ábrán láthatókkal megegyezik), az anyagparamétereket pedig a 3. táblázat foglalja össze irodalmi gyűjtés alapján.
A Yeoh-féle hiperelasztikus, a viszkoelasztikus és a szálerősítés (rebar) anyagparamétereket Yazdandoost és Taheri (2016) és Behroozinia et al. (2020) munkáiból vettük át. A gumiabroncs anyagparamétereinek kísérleti meghatározásáról pedig jó összefoglalást ad Van Blommestein (2016) doktori dolgozata.
|
Anyag |
Anyagmodell |
Modell paraméterek |
Egység |
Irodalom |
|
| öv-acél | Sűrűség | ρ | 7,80E-09 | t/mm3 | Behroozinia et al. (2020)
Van Blommestein (2016) Wang (2011) |
| Elasztikus
(Hook) |
E | 174700 | N/mm2 | Van Blommestein (2016) | |
| µ | 0,3 | – | |||
| huzal-acél | ρ | 5,90E-09 | t/mm3 | ||
| Elasztikus
(Hook) |
E | 206000 | N/mm2 | ||
| µ | 0,3 | – | |||
| szövet-acél | ρ | 1,50E-09 | t/mm3 | ||
| Elasztikus
(Hook) |
E | 16870 | N/mm2 | ||
| µ | 0,3 | – | |||
| peremerősítő-acél | ρ | 1,50E-09 | t/mm3 | ||
| Elasztikus
(Hook) |
E | 9870 | N/mm2 | ||
| µ | 0,3 | – | |||
| peremerősítő-nejlon | ρ | 1,50E-09 | t/mm3 | ||
| Elasztikus
(Hook) |
E | 3970 | N/mm2 | ||
| µ | 0,3 | – | |||
| futófelület gumi | ρ | 7,50E-10 | t/mm3 | Zhang et al. (2020) | |
| Hiperelasztikus
(Yeoh) |
C10 | 6,16E-01 | N/mm2 | ||
| C20 | -1,91E-01 | N/mm2 | |||
| C30 | 4,75E-02 | N/mm2 | |||
| D1 | 8,12E-02 | mm2/N | |||
| D2 | 8,12E-02 | mm2/N | |||
| D3 | 8,12E-02 | mm2/N | |||
| Viszkoelasztikus
(Prony) |
gi | 0,3 | – | Behroozinia et al. (2020) | |
| ki | 0,0 | – | |||
| τi | 0,1 | s | |||
| oldalfal gumi | ρ | 1,05E-09 | t/mm3 | Zhang et al. (2020) | |
| Hiperelasztikus
(Yeoh) |
C10 | 4,88E-01 | N/mm2 | Yazdandoost és Taheri (2016) | |
| C20 | -1,41E-01 | N/mm2 | |||
| C30 | 3,86E-02 | N/mm2 | |||
| D1 | 1,03E-01 | mm2/N | |||
| D2 | 1,03E-01 | mm2/N | |||
| D3 | 1,03E-01 | mm2/N | |||
| Viszkoelasztikus
(Prony) |
gi | 0,3 | – | Behroozinia et al. (2020) | |
| ki | 0,0 | – | |||
| τi | 0,1 | s | |||
| magtöltő gumi | Sűrűség | ρ | 1,05E-09 | t/mm3 | Zhang és mtsai. (2020) |
| Hiperelasztikus
(Yeoh) |
C10 | 8,76E-01 | N/mm2 | Behroozinia et al. (2020) | |
| C20 | -2,93E-01 | N/mm2 | |||
| C30 | 7,94E-02 | N/mm2 | |||
| D1 | 5,71E-02 | mm2/N | |||
| D2 | 5,71E-02 | mm2/N | |||
| D3 | 5,71E-02 | mm2/N | |||
| Viszkoelasztikus
(Prony) |
gi | 0,3 | – | Behroozinia et al. (2020) | |
| ki | 0,0 | – | |||
| τi | 0,1 | s | |||
| görgetett acél | Sűrűség | ρ | 7,80E-08 | t/mm3 | |
| Elasztikus
(Hook) |
E | 210000 | N/mm2 | Van Blommestein (2016) | |
| µ | 0,3 | – | |||
Útpályaszerkezet modellezés végeselem módszerrel
A többrétegű rugalmas rendszerek (MLE) elmélete mellett, Duncan, Monismith, és Wilson (1968) munkájának köszönhetően a végeselemes modellezés (VEM) már az 1960-as évek végén megjelenik az útpályaszerkezetek tanulmányozásában, mivel lehetővé teszi az anyag nemlineáris viselkedésének figyelembevételét (Cho, Tóth, és Soós, 2018). A végeselem-módszer egyik jellegzetes velejárója, hogy az analitikus megoldásoknál használt végtelen tartományokat végessé kell tenni. Ez azonban sokszor nem ésszerű, főleg végtelen vagy félvégtelen kiterjedésű kontinuumokra megfogalmazott feladatok esetében. A probléma útpályaszerkezeteknél a legalsó homogén végtelen féltérnél, vagyis a földműnél jelentkezik. A megoldást a végtelen végeselemek jelentik, amelyekben már végtelenbe nyúló résztartományok is megtalálhatók (Scharle és Szilágyi, 1986).
Az általunk elkészített végeselem modellben az útpályaszerkezet vizsgált tartománya hengeralakú (3.a ábra), ahol a C3D8I (8 csomópontú lineáris) végeselemeket a határfelületen radiális irányban CIN3D8 (8 csomópontú lineáris) végtelen elemek veszik körül (3.b ábra), és a földmű alulról szintén végtelen elemekbe megy át (amik a lesüllyedés nagyságát szabályozzák). Az ABAQUS programban a végtelen elemek létrehozásakor figyelni kell a csomópontok számozására, mivel a végtelen elemeknek csak az első felületét lehet összekapcsolni a végeselemhálóval. A határfelületből kiinduló élek a végtelennek tekintett irányba tartanak és egy pólus körül helyezkednek el. Az elmélet szerint ezen élek mentén van közelítve a távoli tér megoldása, míg az élek határfelületen belüli meghosszabbításai egy pólusban találkoznak. Ebből fakadóan fontos a végtelen irányban elhelyezkedő csomópontok megfelelő pozícionálása; távolságuk a pólustól kétszer akkora, mint a határfelületen fekvőké. A radiálisan elhelyezett végtelen elemek a henger alakú pályaszerkezet modell forgástengelyébe mutatnak, míg a földmű alján lévő végtelen elemek az útburkolat-gumiabroncs kontaktfelületének és a hengeralakú pályaszerkezet modell forgástengelyének metszéspontjában találkoznak.
A gumiabroncs és az útburkolat kontaktfelületének környezetében 6 mm élhosszúságú elemeket hoztunk létre, míg a vizsgált területtől a határfelület felé távolodva rohamosan durvul a háló egészen a 100 mm élhosszig. A háló finomból durvába történő átmenetét lineáris vagy másnéven ragasztott (ún. TIED) kontakttal modelleztük, mivel már a durvább háló elemeiben sem várható nagy feszültséggradiens. Ez az egyszerű megoldás jobb minőségű hálót és gyorsabb futásidőt biztosít. Az útpályaszerkezet minden véges vastagságú rétegében legalább 5 nem-redukáltan integrált elemmel biztosítottuk a hajlításból származó feszültségek megfelelő leképzését. A rétegek egymáson elcsúszni nem tudnak, azokat idealizáltan egymáshoz ragasztva modelleztük. A modellben a térbeli kontinuum elem csomópontjainak 3 elmozdulás (u1, u2, u3) szabadságfoka van, míg a végtelen végeselem végtelen irányban elhelyezett csomópontjainak elmozdulásait alulról a z-tengely, oldalról az x- és y-tengely mentén korlátoztuk. A befogásból eredő feszültségi anomáliák lecsengését az adott pályaszerkezeti réteghez tartozó rugalmas anyagtulajdonsággal rendelkező végtelen elemek biztosítják, és így a peremfeltételek elméletileg nem okoznak nagy hibát a szimulációba.
Gumiabroncs modellezés végeselem módszerrel
2D-s tengelyszimmetrikus modell
A végeselem analízis (bizonyos feltételek teljesülése mellett) lehetőséget ad a 3D-s testek síkbeli vizsgálatára, amivel jelentős számítási idő-, hely- és kapacitás (hardware) spórolható meg. A gumiabroncs felfújásához és keréktárcsára feszítéséhez elegendő egy síkbeli tengelyszimmetrikus feladat megoldása, ami azt jelenti, hogy csak az 1. ábrán látható radiális keresztmetszetet szükséges modelleznünk. Az ABAQUS program megszabja a 2D-s tengelyszimmetrikus feladat leírásához szükséges hengerkoordináta rendszer elhelyezkedését, ahol az x-tengely a sugárirányú (radiális) tengely és az y-tengely a z-tengellyel esik egybe. Ennek megfelelően az abroncs keresztmetszeti modellját az xy-síkban kell elkészítenünk (4.a ábra).
 |
Az ABAQUS programban a tengelyszimmetrikus feladatok definiálásához nem szükséges külön parancsot használni, azonban a hálót kötelezően tengelyszimmetrikus elemekből lehet csak felépíteni. A gumiabroncs modellhez a következő elemtípusokat alkalmaztuk:
- CAX4 (4 csomópontú bilineáris kontinuum-elem) lineárisan rugalmas vagy elasztoplasztikus anyagokhoz.
- CAX4H (4 csomópontú bilineáris hibrid kontinuum-elem) hiperelasztikus anyagokhoz.
- SFMAX1 (2 csomópontú lineáris membrán-szerű felületelem) a szálerősítéshez.
A felületelemek felépítésüket tekintve vastagsággal nem rendelkező membrán elemek. Általában többletsúly definiálásakor vagy felületre ható erők felvitelénél alkalmazzuk őket, de jól megfelelnek a gumiabroncs szálerősítésének (rebar) egyszerűsített figyelembevételéhez is. Az SFMAX1 felületelem nagy előnye, hogy a szálerősítésnek csak a radiális metszetben szükséges a lefutását modellezni, a szálerősítés keresztmetszetét a végeselem hálótól független paraméterekkel tudjuk megadni. További előny még, hogy nem kell a felületelemeknek a végeselemhaló egyéb elemeihez csomópontjaikkal csatlakozniuk, hanem ún. beágyazott elemekként (embeded element) definiálhatók. A gumiabroncs modellnél a gumi anyaga a szálerősítéshez hozzárendelt „gazda-elem”.
A tengelyszimmetrikus modell befogása a kerék forgástengelyének és az abroncs szimmetria tengelyének metszéspontjában van (4.b ábra). A befogási pont 2. (U2) és 6. (UR3) szabadságfokát (degrees of freedom, DOF) korlátozni szükséges, hogy a forgástengely mentén ne történhessen elmozdulás, illetve a radiális metszet ne tudjon a síkjába elfordulni. A gumiabroncs modell keresztmetszete az 4.a ábrán még nem a keréktárcsára feszített és nyomás alá helyezett állapotot tükrözi. A keréktárcsa és a gumiabroncs interakcióját Jeong (2016) szálerősítés szakadás vizsgálata alapján dolgoztuk ki. A szimuláció kezdetekor a karikahuzalban – hosszanti irányban – 30 MPa nagyságú húzófeszültséget adunk meg, ami az abroncs peremét finoman a keréktárcsára feszíti. Az abroncs pereme a felfújás közben a keréktárcsán elcsúszhat (a súrlódási tényezőt 0,3-nak választottuk), valamint radikális túlnyomás esetén akár le is válhat arról (4.c ábra). Ennél a pontnál a gumiabroncsban ébredő feszültségeket és a felfújt abroncsalakot már érdemes összevetni a méréseinkkel (Jeong, 2016; Korunovic, Trajanovic, és Stojkovic, 2007). A későbbi gumiabroncs-útburkolat kontaktszimulációra tekintettel már a tengelyszimmetrikus modellnél megadtuk a futófelület érintkezési felületét.
3D-s teljes testmodell
A gumiabroncs 2D-s tengelyszimmetrikus modellje a kontaktfelületek ellenére is egy rendkívül gyorsan lefutó szimuláció, ami egy normál munkaállomáson (workstation, 4 CPU, magonként 3.5GHz órajel) egy perc alatti futásidőt jelent. Ugyanez a feladat térben – változatlan gépteljesítmény mellett is – több tíz percet igényel. A következő lépésekhez viszont, ahol az útburkolat és a gumiabroncs interakcióját vizsgáljuk már elengedhetetlen, hogy növeljük a végeselem modell komplexitását. Az ABAQUS program szerencsére képes a 2D-s tengelyszimmetrikus modellből a *SYMMETRIC MODELL GENERATION paranccsal 3D-s modellt létrehozni úgy, hogy projektálja a 3D-s hálóra a tengelyszimmetrikus modell feszültségállapotát. Ezt követően még egy egyensúlyi számításra (equlibrium step) van szükség, aminek a hatására az átvetített feszültségi állapot a 3D-s modellben ténylegesen egyensúlyi állapotba kerül.
 |
A gumiabroncs 3D-s teljes testmodell generálásánál érdemes azokat a részeket finomabban hálózni, ahol a gumiabroncs-útburkolat interakció várható és a többi elemet durvábban közelíteni, ezzel is spórolva a számításhoz szükséges idővel és gépteljesítménnyel (5. ábra). A modell durvábbra hálózott részein ezért a CCL12 henger alakú végeselemeket alkalmaztuk, amelyek a kerületi irányban elhelyezett plusz csomópontjaikkal az ívelt térrészeket jobban letudják követni. Kontaktfelületnek ajánlatos hagyományos elemeket választani, hogy a megoldás gyorsabban elérje a stabil egyensúlyi helyzetet.
A 3D-s modell generálásakor a tengelyszimmetrikus modellben létrehozott csomópont-, elem- és kontaktfelület csoportok automatikusan létrejönnek, ezért adtuk meg már a 2D-s modellben a gumiabroncs-útburkolat interakcióhoz szükséges kontaktfelületeket. Ennél a lépésnél szükséges az *INCLUDE paranccsal az útpályaszerkezet modellt beolvasni. Érdemes az útburkolat hálóját az abroncstól távolabb elhelyezni, hogy azok még ne érjenek össze. A gumiabroncs-útburkolat kontaktszimulációhoz meg kell adni a kontaktpárokat és az interakciós tulajdonságokat. A helyes kontaktdefiniáláshoz a „puhább” anyagot, azaz a gumiabroncs futófelületét szükséges finomabban hálózni és így azt „slave” felületnek választani a kontaktpárban. Mivel jelen munkában csak a statikus terhelés esetét vizsgáltuk, az útburkolat (kopóréteg) és az abroncs között nem definiáltunk komplex súrlódási modellt. Nakajima (2019) és Zhou et al. (2015) is megállapítják, hogy az abroncslenyomat számításához a súrlódásmentes érintkezési kapcsolat valósághűbb eredményeket hoz. Ez azzal magyarázható, hogy a súrlódás hatására az abroncs profilmintájának peremén nyírófeszültségek ébrednek és begyűrődések keletkeznek. Ez a szcenárió az abroncs gördülő mozgásakor, illetve a gördülő mozgásból levezetett álló helyzetében nem jelentkezik. Az abroncs befogása továbbra is azonos pontban történik a 3D-s modellben, azonban mind a 6 szabadságfokot korlátozzuk, valamint az abroncs belső légnyomását is megoszló terhelésként vesszük figyelembe.
Gumiabroncs-útburkolat kontakt szimuláció
A kutatás elsődleges célja annak megállapítás, hogy az ikerabroncs érintkezési nyomása (q) és felülete (A) hogyan függ a kerékterhelés (F) nagyságától, valamint mekkora igénybevételek lépnek fel a kerékterhelés hatására a vizsgált hajlékony és félmerev szerkezeteken belül. Mivel a klasszikus méretezési eljárások az útpályaszerkezetet terhelő ikerabroncsok lenyomatát egy sugarú körtárcsán egyenletesen megoszló erőrendszerrel veszik számításba, ezért ezt a terhelési esetet is kiszámoltuk összehasonlításul. A 6.a ábra a valóságos kerékelrendezést és terhelést, míg a 6.b ábra az azzal ekvivalens kontaktfelületű, helyettesítő körtárcsa modellt szemlélteti.
 |
A méretezési feladatok megoldásánál rendszerint megelégszünk azzal, hogy csak a terhelés tengelyében a kritikus helyeken ismerjük az igénybevételeket, mivel ezek lesznek mértékadók. A mértékadó igénybevételek helye a kohézióval rendelkező szerkezeti anyagok esetében a terhelés tengelyében a réteg alsó szála, a kohézióval nem rendelkező szerkezeti anyagok esetében (szemcsés rétegek és földmű) a réteg teteje. A 6. ábrán narancssárga pontok jelzik a vizsgálati helyeket:
- A) Burkolat függőleges elmozdulása (behajlása)
- B) Az alsó aszfaltréteg alján ébredő vízszintes fajlagos megnyúlás
- C) A földműréteg tetején ébredő függőleges fajlagos összenyomódás
A 6.a ábrának megfelelő terhelési esetet vizsgáltuk részletesen a végeselem módszerrel (ABAQUS), míg a 6.b ábrán látható modellt a többrétegű rugalmas rendszerek (MLE) elméletét felhasználva számítottuk ki a WESLEA (Waterways Experiment Station Layered Elastic Analysis) programmal (lásd később).
A gumiabroncs-útburkolat végeselem kontakt szimuláció az egyensúlyi állapotba helyezett 3D-s abroncsmodell analízisének a folytatása, így itt már nincs lehetőség további módosításokra. Az egyes számítási lépésekben (load step) legfeljebb csak a paraméterek értékén pl. súrlódási tényező tudunk változtatni.
A lenyomat vizsgálat első lépése, hogy az abroncsmodellt hozzányomjuk az útburkolathoz. A konvergencia miatt praktikus – a kontakt létrejöttéig – az abroncs befogására egy rögzített eltolást, mint peremfeltételt megadni. Kezdetben a felfújt gumiabroncs futófelülete és az útburkolat 2 mm-re található egymástól. Az előtolást 6 mm-nek választottuk, ami a befogásban (egy abroncs esetén) mintegy 1600 N ellenerőt jelentett.
|
Gumiabroncsnyomás [kPa] |
Egy abroncsra jutó F/2 terhelés nagysága [kN] |
||
|
Üzemi terhelés |
Túlterhelés |
Extrém túlterhelés |
|
| 430 | 17,5 | 20,0 | 22,5 |
| 530 | 20,0 | 22,5 | 25,0 |
| 630 | 22,5 | 25,0 | 27,5 |
| 730 | 25,0 | 27,5 | 30,0 |
| F/2 [kN] |
p [kPa] |
L1 [mm] |
L2 [mm] |
a [mm] |
qmax [kPa] |
q [kPa] |
A [mm2] |
hq [mm] |
|
|
hajlékony |
félmerev |
||||||||
| 17,5 | 430 | 240 | 186 | 169 | 825 | 391 | 44757 | 60,8 | 63,2 |
| 20,0 | 430 | 240 | 202 | 176 | 1030 | 413 | 48426 | 56,3 | 58,9 |
| 22,5 | 430 | 240 | 218 | 182 | 1242 | 431 | 52204 | 51,5 | 54,2 |
| 20,0 | 530 | 240 | 189 | 170 | 789 | 440 | 45455 | 66,7 | 69,8 |
| 22,5 | 530 | 240 | 200 | 175 | 967 | 469 | 47974 | 62,4 | 65,3 |
| 25,0 | 530 | 240 | 221 | 184 | 1151 | 471 | 53079 | 64,3 | 67,8 |
| 22,5 | 630 | 240 | 194 | 172 | 874 | 484 | 46488 | 71,9 | 75,4 |
| 25,0 | 630 | 240 | 202 | 176 | 919 | 516 | 48450 | 67,6 | 71,1 |
| 27,5 | 630 | 240 | 225 | 185 | 1077 | 510 | 53922 | 72,1 | 76,5 |
| 25,0 | 730 | 240 | 197 | 173 | 953 | 530 | 47170 | 74,8 | 78,5 |
| 27,5 | 730 | 240 | 205 | 177 | 1010 | 560 | 49107 | 71,8 | 75,6 |
| 30,0 | 730 | 240 | 224 | 185 | 1054 | 557 | 53860 | 75,6 | 80,0 |
A szimuláció további részében fokozatosan ráadtuk a pontszerű függőleges kerékterhelést a modellre, aminek hatására a kontaktfelület kiterjedt. A lenyomat létrejöttéig fontos, hogy a súrlódást nullának válasszuk, mert az abroncs profilja így jobban szét tud terülni az útburkolaton, nem ébrednek magas nyírófeszültségek a lenyomat kialakulása közben, és így a gumiabroncs deformációja is jobban megegyezik a gördüléskori állapottal. A gumiabroncs-útburkolat kontakt szimuláció mátrixot a 4. táblázat foglalja össze, aminek összeállításánál figyelembe vettük az abroncsgyártó (megengedett terhelés és gumiabroncsnyomás) ajánlását is. Ennek megfelelően nem csak az előírt üzemi terhelés-nyomásérték szcenáriót, hanem az alacsony nyomású gumiabroncs viselkedést is szimuláltuk.
Eredmények és megvitatásuk
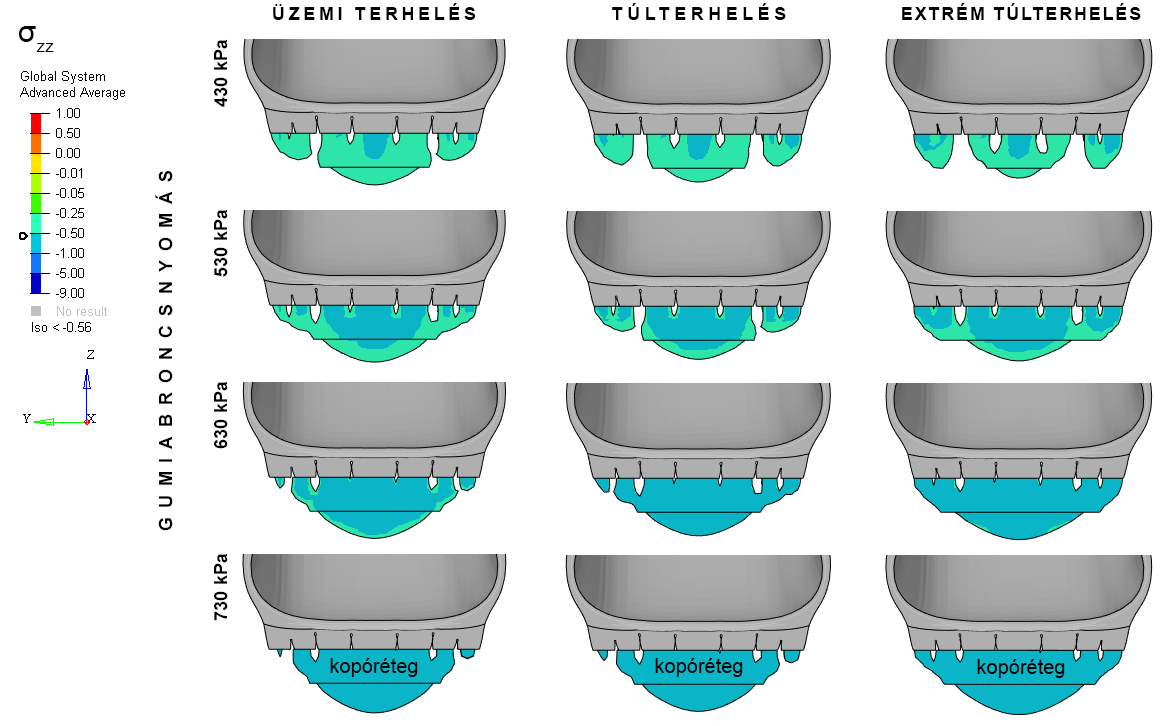
A gumiabroncs-útburkolat kontakt szimulációt a 4. táblázat minden gumiabroncsnyomás és kerékterhelés esetére lefuttattuk a hajlékony és a félmerev útpályaszerkezeteken. Eredményül a szerkezetekben fellépő igénybevételeket és az útburkolaton kialakuló abroncslenyomatokat és kontaktfeszültségeket kaptuk, amik jól visszaadták a szakirodalomban közölt értékeket (W. Wang, Yan, és Zhao, 2013; Zhou et al. 2015). Mind a két szerkezettípusnál az érintkezési felület alakját legjobban egy \(L_{1}\) x \(L_{2} \) nagyságú téglalappal tudtuk közelíteni (7.a ábra), az ikerlenyomatok nagyságát (A), a helyettesítő kör sugarát (a) és a fellépő kontaktfeszültségeket ( \(q_{max}\) és q) pedig az 5. táblázatban foglaltuk össze. Mivel az elemzések azt mutatták, hogy a vizsgált két útpályaszerkezet felépítés semmilyen hatással nem bírt a gumiabroncs-útburkolat érintkezési kapcsolatra, ezért az 5. táblázat értékei mind a két szerkezettípusra érvényes.
Üzemi nyomás és legnagyobb megengedett kerékterhelés mellett a kontaktfeszültségek eloszlása ellipszoidnak tekinthető (7.b ábra), de alacsony abroncsnyomásnál a futófelület egyenlőtlenül érintkezik az útfelülettel, az abroncs közepe kissé elemelkedik és a terhelést a gumiabroncs merevségéből következően már annak két oldala veszi fel.
 |
Az elmondottakból következik, hogy a teherelosztás nem lesz egyenletes (7.c-d ábra) és a kialakuló feszültségcsúcsok (\(q_{max}\) ) az átlagos kontaktnyomás 2,5-3,0 szorosát is elérhetik. Ez azonban nem okoz problémát, ha nem a kopóréteg igénybevételeit vagy a nyomvályúképződés folyamatát vizsgáljuk, mivel méréseink szerint az útburkolat felszíne alatt \(h_{q}=5-8\) centiméterre már ezek a túlnyomások kiegyenlítődének. A 8. ábrasorozat mutatja be a q átlagos kontaktnyomásnál nagyobb feszültségzónákat az ikerabroncsok alatt. Jól látható, hogy a 6. ábrán jelölt B pont jóval mélyebben helyezkedik el, mint a átlagos feszültségpontokat összekötő görbék maximuma, így az ott ébredő igénybevételeket \(q_{max}\) elhanyagolása már nem befolyásolja jelentősen. A félmerev útpályaszerkezetnél 3-5 mm-rel nagyobb \(h_{q}\) határmélységet mutattunk ki, mint a hajlékony útpályaszerkezetnél. Ez a merevebb szerkezetek túlterhelésre való érzékenységével magyarázható. Összességében a kontakt szimuláció eredményei jól visszaadták a valódi gumiabroncsokról szerzett ismereteinket, így az abroncsmodellt további elemzésekre alkalmasnak ítéltük.
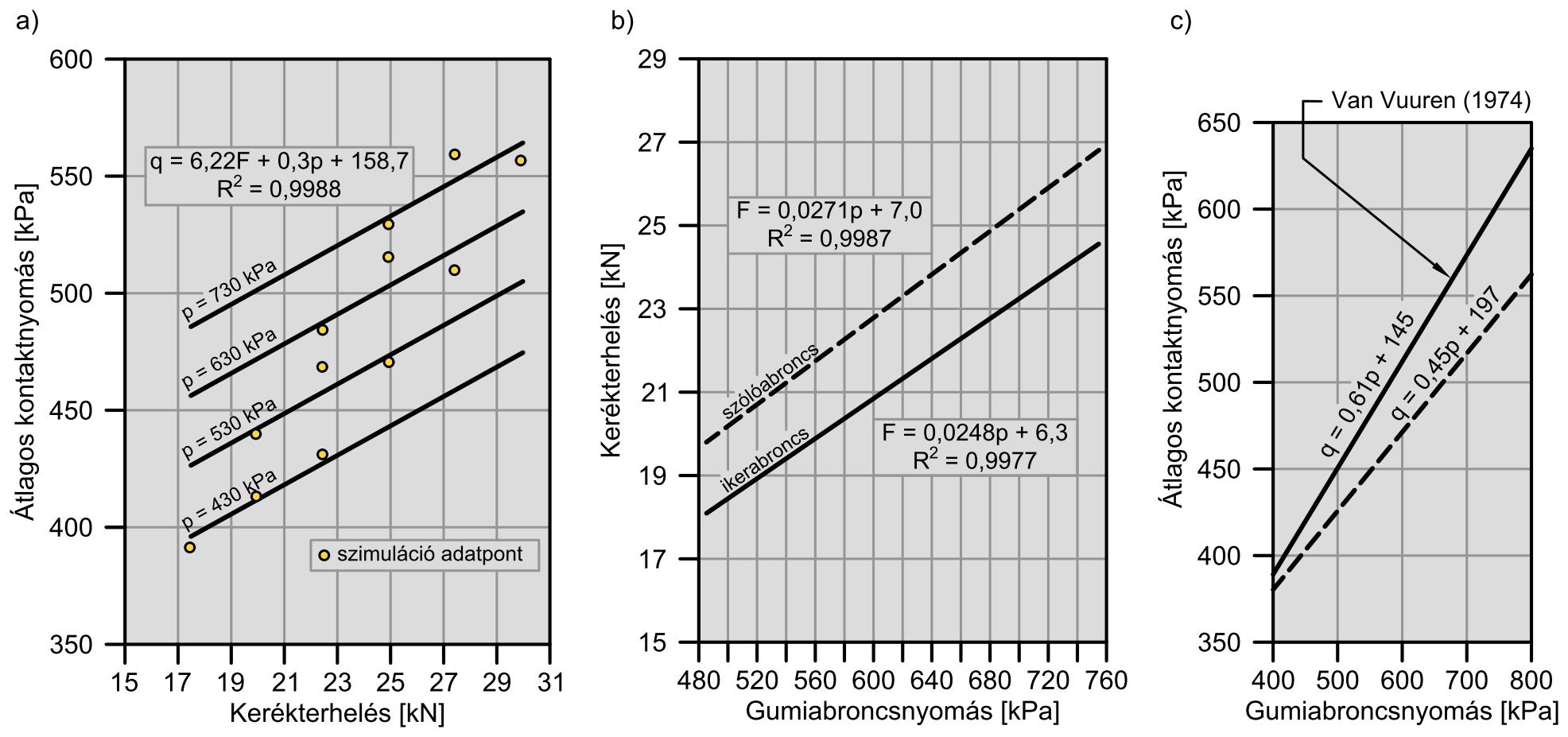
A továbbiakban kapcsolatot kerestünk az átlagos q kontaktnyomás, az F kerékterhelés és a p gumiabroncsnyomás között. Felhasználtuk Van Vuuren (1974) laboratórium mérésekre alapozott (5) számú empirikus összefüggését (9.a ábra). A függvény együtthatóit a legkisebb négyzetek módszerével határoztuk meg az 5. táblázat adatait felhasználva (R2 = 0,99):
 |
\[ q=6,22F+0,3p+158,7 \]
A kontaktszimuláció szerint a p és F együttes (kevert) hatása nem kimutatható, ellenben az abroncs „hajlékonyságára” jellemző C’ konstans fontosságát a végeselem szimuláció is megerősítette. Figyelembe véve, hogy az abroncsgyártók az üzemi működésre megadják a megengedett gumiabroncsnyomás és kerékterhelés értékeket, a fenti (10) összefüggés tovább egyszerűsíthető (9.b ábra). Gyártói adatlap alapján a megengedett kerékterhelés és abroncsnyomás összefüggést egy lineáris függvénykapcsolat adja meg (R2 = 0,99):
\[ F=0,248p+6,30 \]
Végül (11) egyenletet behelyettesítve a (10) egyenletbe kapjuk az üzemi körülményekre vonatkozó átlagos kontaktnyomás és gumiabroncsnyomás összefüggést:
\[ q=0,454p+197,87 \]
A (12) összefüggéssel a burkolatra jutó átlagos q kontaktfeszültséget a gumiabroncs belső légnyomásából tudjuk megbecsülni. Van Vuuren (1974) eredeti munkájában több gyártó pl. Michelin, Firestone, Goodyear, General gumiabroncsira is elvégezte a fenti elemzést, és a laboratóriumi mérések átlagolásával hasonló lineáris összefüggésre jutott, mint mi. Ábrázolva a két modellegyeneset (9.c ábra), jól láthatjuk, hogy az egy abroncsra lefuttatott végeselem szimuláció eredménye az „átlagos” egyeneshez igen közel esik, így azt igazoltnak tekinthetjük. Meg kell azonban jegyeznünk, hogy a (12) egyenlet csak radiális kialakítású és nem gördülő abroncsra igaz. De Beer és mtsai. (1997) szerint Van Vuuren (1974) modellje gördülő diagonál gumiabroncsoknál alábecsüli az ébredő kontaktfeszültséget és használatát nem javasolják.
Gyakorlati számításoknál pl. burkolat megerősítésnél az ikerabroncsok által terhelt felületet olyan körrel helyettesítjük, aminek a felülete megegyezik a tényleges érintkezési felülettel (Soós és Tóth 2016). A helyettesítő kör átmérőjét Baksay (1974) az alábbi összefüggéssel közelítette (Boromisza, 1997):
 |
\[ D≈562,5√F/q \]
| ahol: | |
| \(D\) | anyagparaméterek [Pa] |
| \(F\) | deformációs invariáns |
| \(p\) | összenyomhatatlansági paraméterek [1/Pa] |
Mivel a (12) összefüggés szerint a függvénye, ezért a (13) összefüggésben a p=q helyettesítéssel már nagyon pontosan megkapjuk a keresett helyettesítő kör α sugarát:
\[ D≈562,5√F/q \]
ahol α mm-ben és q kPa-ban van értelmezve. A (14) összefüggés az 5. táblázat adatait tökéletesen visszaadja. Baksay (1974) az abroncslenyomat felületének tényleges megmérése alapján számította ki a helyettesítő kör méreteit és állította fel összefüggését, amit a mi végeselemes szimulációnk is megerősített.
Az átlagos q kontaktnyomások ismeretében a WESLEA programmal kiszámoltuk a hajlékony és félmerev szerkezetek kritikus pontjaiban (A, B, C) az igénybevételeket, és azokat összehasonlítottuk az ikerabroncs végeselem kontaktszimuláció eredményeivel (6. táblázat). A legnagyobb eltéréseket a 6. táblázat adataiban a függőleges \(u_{zz} \) elmozdulásoknál, vagyis a behajlásoknál találtuk (A pont). Mind a két vizsgált szerkezetnél a végeselem pályaszerkezeti modell – a végtelen elemek ellenére is – jelentősen kisebb (hajlékony 40%, félmerev 50%) behajlásokat eredményez, mint a rugalmas rétegek elméletén alapuló számítás. Ennek egyik magyarázata, hogy ikerabroncsok esetén a maximális elmozdulás nem a terhelés szimmetriatengelyében, hanem az egyes kerekek tengelyében lép fel, amit a 10. ábra függőleges normális \(σ_{zz} \) nyomófeszültség eloszlása is jól igazol. Másrészt a Burmister (1945a; 1945b; 1945c) elméletén alapuló WESLEA program a függőleges fajlagos alakváltozásokat a végtelenig összegzi, így az a valósághoz képest nagyobb elmozdulásokat ad. A behajlásoknál tapasztalt nagy eltérésekre leginkább a függőleges alakváltozáson alapuló teherbírásmérési módszerek pl. Benkelman-gerenda, Lacroix-mérőkocsi vagy Curviameter eredményeinek kiértékelésénél kell odafigyelnünk (Tóth, 2007; Tóth & Tóth, 2008).
 |
 |
 |
 |
| F/2 [kN] | q [kPa] |
Ikerabroncs (VEM) |
Helyettesítő körtárcsa (MLE) |
|||||
| A [µm] |
B [µstrain] |
C [µstrain] |
A [µm] |
B [µstrain] |
C [µstrain] |
|||
|
uzz |
εxx |
εyy |
εzz |
uzz |
εt |
εv |
||
|
A hajlékony útpályaszerkezetben ébredő igénybevételek |
||||||||
| 17,5 | 391 | 190 | -64,23 | -37,33 | 172,79 | 310 | -68,83 | 195,19 |
| 20,0 | 413 | 217 | -72,65 | -43,00 | 196,97 | 352 | -75,76 | 221,19 |
| 22,5 | 431 | 244 | -80,73 | -48,67 | 220,97 | 394 | -82,27 | 246,77 |
| 20,0 | 440 | 217 | -73,05 | -42,19 | 196,69 | 354 | -78,34 | 222,87 |
| 22,5 | 469 | 243 | -81,51 | -47,80 | 220,82 | 397 | -86,81 | 249,89 |
| 25,0 | 471 | 270 | -89,68 | -53,42 | 244,75 | 439 | -93,68 | 275,79 |
| 22,5 | 484 | 242 | -81,71 | -46,99 | 220,25 | 398 | -87,58 | 250,38 |
| 25,0 | 516 | 269 | -90,18 | -52,56 | 244,31 | 441 | -96,19 | 277,48 |
| 27,5 | 510 | 296 | -98,42 | -58,14 | 268,24 | 483 | -102,56 | 303,03 |
| 25,0 | 530 | 268 | -90,17 | -51,71 | 243,31 | 442 | -96,92 | 277,95 |
| 27,5 | 560 | 294 | -98,63 | -57,24 | 267,32 | 485 | -105,41 | 304,96 |
| 30,0 | 557 | 321 | -106,92 | -62,77 | 291,21 | 527 | -111,93 | 330,61 |
|
A félmerev útpályaszerkezetben ébredő igénybevételek |
||||||||
| 17,5 | 391 | 125 | -29,71 | -14,01 | 110,34 | 249 | -32,34 | 130,02 |
| 20,0 | 413 | 143 | -33,51 | -16,28 | 125,73 | 284 | -35,94 | 149,88 |
| 22,5 | 431 | 161 | -37,12 | -18,57 | 140,97 | 318 | -39,32 | 167,48 |
| 20,0 | 440 | 143 | -33,78 | -15,73 | 125,59 | 285 | -36,76 | 150,69 |
| 22,5 | 469 | 160 | -37,61 | -17,97 | 140,95 | 320 | -40,57 | 168,75 |
| 25,0 | 471 | 178 | -41,27 | -20,22 | 156,16 | 353 | -43,41 | 185,80 |
| 22,5 | 484 | 159 | -37,76 | -17,43 | 140,62 | 320 | -41,03 | 169,20 |
| 25,0 | 516 | 177 | -41,60 | -19,64 | 155,94 | 355 | -44,92 | 187,34 |
| 27,5 | 510 | 195 | -45,32 | -21,87 | 171,15 | 388 | -47,47 | 204,08 |
| 25,0 | 530 | 176 | -41,65 | -19,11 | 155,33 | 356 | -45,35 | 187,77 |
| 27,5 | 560 | 194 | -45,49 | -21,29 | 170,61 | 390 | -49,16 | 205,83 |
| 30,0 | 557 | 211 | -49,23 | -23,49 | 185,81 | 424 | -51,80 | 222,66 |
A kialakuló nyírófeszültségeloszlás szimmetrikus, ahol a szimmetriatengely a két abroncs között van, maximuma a kopóréteg alatt, a kerékterhelés szélén lép fel (11. ábra), ami a nagyszilárdságú kötőréteg fontosságára hívja fel a figyelmet. Az aszfaltréteg alsó szálában a B pontban ébredő vízszintes x- és y-irányú \(ε_{xx}\) és \(ε_{yy} \) és fajlagos nyúlások értékei az ikerabroncs végeselem modellben jelentősen eltérnek egymástól ( ), míg a helyettesítő tárcsamodellnél – a terhelési szimmetriából következően – megegyeznek egymással ( \(ε_{t}=ε_{xx}=ε_{yy} \) ). A méretezés szempontjából a mértékadó, a haladó kerék hosszmetszetével megegyező \(ε_{xx}\) vagy \(ε_{τ} \) fajlagos nyúlásértékek fontosak a számunkra. A végeselem szimuláció és a WESLEA program eredményei mind a két szerkezettípus esetében nagyon szoros, kb. 5-8%-os eltéréssel mutattak egyezést, mivel a 12. ábra alapján az ikerabroncs elrendezésnél is a terhelés tengelyében ébrednek a legnagyobb nyúlások. A földműréteg tetején a C pontban ébredő függőleges \(ε_{zz} \) vagy \(ε_{v} \) fajlagos összenyomódásoknál már magasabb, kb. 10-15%-os eltérést tudtunk kimutatni az analitikus megoldás javára, de ezt még mindig igen jó egyezésnek mondhatjuk. A 13. ábra alapján az ikerabroncs elrendezésnél nem az egyes kerekek tengelyében, hanem a terhelés szimmetriatengelyében lép fel a maximális fajlagos \(ε_{zz} \) összenyomódás. A 6. táblázat adatai alapján az állapítható meg, hogy az aszfaltrétegek fáradási (B pont) és az altalaj-összenyomódási (C pont) kritériumokhoz a mértékadó igénybevételeket az ikerabroncs terhelést helyettesítő tárcsamodellel jól meg lehet becsülni, ha a q átlagos kontaktfeszültségeket reálisan választjuk meg. A lehajlási kritériumhoz szükséges mértékadó behajlás (A pont) számításánál, már nem igaz ez a megállapítás.
Összefoglalás
Az ABAQUS programban sikerült több lépésen keresztül felépítenünk a gumiabroncs-útburkolat érintkezési kapcsolatának komplex végeselem modelljét. A kiindulást a gumiabroncs 2D-s tengelyszimmetrikus modellje adta, amivel az abroncs felfújását és keréktárcsára feszítését tudtuk szimulálni. A következő lépésben a 2D-s tengelyszimmetrikus modellből létrehoztuk a 3D-s teljes testmodellt, ami az ABAQUS programban egyetlen paranccsal megoldható. Az így keletkezett 3D-s hálóra átvetítettük a tengelyszimmetrikus modell feszültségi állapotát, majd egyensúlyi állapotba helyeztük azt. A gumiabroncs után következet az útpályaszerkezetek végeselem modelljének elkészítése. Az útpályaszerkezetek legalsó rétegét (a földművet) végtelen elemekkel modelleztük, így jelentősen tudtuk csökkenteni a szükséges végeselemek számát és a számítási időt. Meghatároztuk a gumiabroncs-útburkolat kontaktszimulációhoz a kontaktpárokat és az interakciós tulajdonságokat. Végül az ikerabroncs kerékterhelést ráhelyeztük a vizsgált hajlékony és félmerev útpályaszerkezetekre. A létrejövő kontaktlenyomatok és kontaktfeszültségek jól visszaadták a szakirodalomban közölt értékeket. A végeselem szimuláció elkészítésében nagy segítésünkre volt az ABAQUS program kézikönyve (Dassault Systèmes 2014), amiben rendkívül sok hasznos információt és egyszerűbb példákat is találunk. Nehézséget okozott viszont a gumiabroncs modell összeállításánál, hogy a fellehető források nagy részében hiányos a dokumentáció, aminek egy része valószínűleg a nem publikus gyártói információkkal magyarázható.
Mivel a szimuláció eredményei, vagyis a kontakt feszültségek és lenyomatok jól egyeztek a szakirodalmi adatokkal, ezért a továbbiakban kapcsolatot kerestünk az átlagos q kontaktnyomás, az F kerékterhelés és a gumiabroncsnyomás között. Vizsgálataink azt mutatták, hogy Van Vuuren (1974) laboratórium mérések alapján felállított összefüggése még mindig jól használható az átlagos kontaktfeszültség számítására, mivel a túlterhelt abroncsokra jellemző nem egyenletes teherelosztás következtében ébredő feszültségcsúcsok az útburkolat felszíne alatt 5-8 centiméterre már kiegyenlítődnek. A kontaktlenyomatokkal egyenértékű helyettesítő kör sugarát Baksay (1974) által javasolt (13) összefüggés pontosan megadja a p = q helyettesítéssel. Az átlagos kontaktfesztültség és a helyettesítő kör sugarának ismertében összehasonlító számításokat végeztünk az ikerabroncs végeselem szimuláció és a helyettesítő körtárcsamodell között. A legnagyobb eltérést a központi behajlásnál találtuk, az útpályaszerkezetek többi vizsgált pontjában a végeselem szimuláció eredményei jó egyezést mutattak a WESLEA program számításaival. Ezért az aszfaltréteg fáradási és az altalaj-összenyomódási kritériumokhoz a mértékadó igénybevételeket a helyettesítő körtárcsamodellel számíthatjuk, ha a q átlagos kontaktfeszültséget ismerjük.
Jelen munkában bemutatott gumiabroncs végeselem modell elég összetett volt az érintkezési kapcsolat részletes elemzéséhez, de megfelelő anyagparaméterekkel a modell további vizsgálatokhoz is felhasználható, mint amilyen például: a használat közbeni hőképződés (termikus kölcsönhatás), a gördülési zaj (noise, vibration, and harshness, NVH), a vízre felúszás (aquaplaning) vagy az abroncskopás jelensége. Az útpályaszerkezetek végeselem modellje szinte változatlan felépítése mellett továbbfejleszthető a viszkoelasztikus (vagy akár a viszkoelasztoplasztikus) anyagmodell és a rétegek közötti elmozdulás figyelembevételével. Az ilyen irányú fejlesztésekkel pedig a jövőben olyan „virtuális útpályaszerkezet labor” alakítható ki, amivel a nagyon költséges helyszíni vizsgálatok jelentős köre kiváltható vagy kiegészíthető lesz, valamint a vitás szakmai kérdések gyors megválaszolására nyílik lehetőség.
Köszönetnyilvánítás
A publikáció elkészítését az EFOP-3.6.2-16-2017-00018 („Termeljünk együtt a természettel – az agrárerdészet mint új kitörési lehetőség”) projekt támogatta.
Irodalomjegyzék
Adorjányi, K. 2009: Bemenő paraméterek bővítése az aszfaltburkolatú pályaszerkezetek méretezésénél. Közlekedésépítési szemle 59 (7): 11–17.
Behroozinia, P., Seyedmeysam, K., Saied, T. & Reza, M. 2020: „An Investigation Towards Intelligent Tyres Using Finite Element Analysis”. International Journal of Pavement Engineering 21 (3): 311–21. https://doi.org/10/ghcp2m
Boromisza, T. 1997: Aszfaltburkolatú útpályaszerkezetek méretezésének gyakorlata: Méretezési Praktikum. Közúti Közlekedési Füzetek 16. Budapest: Közlekedési, Hírközlési és Vízügyi Minisztérium.
Brinson, Hal F. & L. Catherine, B. 2015: Polymer Engineering Science and Viscoelasticity. Boston, MA: Springer US. https://doi.org/10.1007/978-1-4899-7485-3
Burmister, D. M. 1945a: The General Theory of Stresses and Displacements in Layered Systems. I. Journal of Applied Physics 16 (2): 89–94. https://doi.org/10/cvd4kk
———. 1945b: The General Theory of Stresses and Displacements in Layered Soil Systems. II. Journal of Applied Physics 16 (3): 126–27. https://doi.org/10/b9zg45
———. 1945c: The General Theory of Stresses and Displacements in Layered Soil Systems. III. Journal of Applied Physics 16 (5): 296–302. https://doi.org/10.1063/1.1707590
Dassault Systèmes. 2014: Abaqus 6.14 Online Documentation. 2014. április 23. http://ivt-abaqusdoc.ivt.ntnu.no:2080/texis/search/?query=wetting&submit.x=0&submit.y=0&group=bk&CDB=v6.14.
De Beer, M., Fisher, C. & Jooste, F. J. 1997: Determination of Pneumatic Tyre/Pavement Interface Contact Stresses Under Moving Loads and Some Effects on Pavements with Thin Asphalt Surfacing Layers. In Eighth International Conference on Asphalt Pavements, Seatlle Usa; August 10-14, 1997: Paper, szerkesztette H. J Ertman Larsen, 1:179–227. Roskilde: Road Directorate, Danish Road Institute.
Duncan, J. M., Monismith, C. L. & Wilson, E. L. 1968: Finite Element Analyses of Pavements. Highway Research Record 228: 18–33.
Fazekas, B. & Goda. T. 2017: Gumiszerű anyagok hiper-viszkoelasztikus anyagmodell paramétereinek meghatározása. Gép LXVIII. (3): 54–57.
Alan Neville, G., & Walter, J. D. 2006: The Pneumatic Tire. DOT HS 810 561. The University of Akron. http://works.bepress.com/joseph_walter/7/.
Hernandez, J. A., Gamez, A., Shakiba, M. & Al-Qadi, I. L. 2017: Numerical Prediction of Three-Dimensional Tire-Pavement Contact Stresses. Technical Report ICT-17-004. Taxas A&M University. http://hdl.handle.net/2142/95142.
Jeong, K. M. 2016: Prediction of Burst Pressure of a Radial Truck Tire Using Finite Element Analysis. World Journal of Engineering and Technology 04 (02): 228–37. https://doi.org/10/gf9tdc
Kakucs, A. 2020: A végeselem-módszer alapjai. Jegyzet. Sapientia Erdélyi Magyar Tudományegyetem.
Kennedy, R. H. 2003: Experiences with Cylindrical Elements in Tire Modeling. In ABAQUS Users’ Conf, 247. http://www.simulia.com/download/solutions/automotive_cust%20references/tires_experience_auc03_hankook.pdf.
Kézdi, Á. 1954: Talajmechanika II. Budapest: Tankönyvkiadó.
Lawton, W. L. 1957: Static Load Contact Pressure Patterns Under Airplane Tires. In Highway Research Board Proceedings, 36:233–39. Highway Research Board.
Lister, N. W. & Nunn, D. E. 1968: Contact Areas of Commercial Vehicle Tyres. London: Transport and Road Research Laboratory. https://trl.co.uk/sites/default/files/LR172.pdf.
Madocsai, G., Veress, Á. & Palkovics, L. 2011: Gumialkatrészek viselkedésének vizsgálata jármű-mechatronikai rendszerekben. In Innováció és Fenntartható Felszíni Közlekedés 2011, 21–33. Budapest.
McCullough, B. F., & Boedecker. K. J. 1969: Use of Linear-Elastic Layered Theory for the Design of CRCP Overlays. Highway Research Record 2: 1–13.
Molnár, L. 2011: CAD alapjai. EDUTUS Főiskola.
Nakajima, Y. 2019: Advanced Tire Mechanics. Singapore: Springer Singaporehttps https://doi.org/10.1007/978-981-13-5799-2
Nemesdy, E. 1992: Az új magyar típus-útpályaszerkezetek mechanikai méretezésének háttere. Közlekedésépítés- és mélyépítéstudományi szemle : a Közlekedéstudományi Egyesület lapja 42 (8): 293–306.
Scharle, P. & Szilágyi, Gy. 1986: A végeselem-módszer vegyes analitikus eljárásai. Budapest: Műszaki Könyvkiadó.
Seoyoung, C., Tóth, Cs. & Soós, Z. 2018: Finite Element Method Analysis for Mechanistic Design in Flexible Pavement, Review: From How to Build a Material in FE Analysis to Complexity in Reality. Epitoanyag – Journal of Silicate Based and Composite Materials 70 (6): 204–8. https://doi.org/10/gfvbkb
Soós, Z. & Tóth, Cs. 2016: Simple Overlay Design Method for Thick Asphalt Pavements Based on the Method of Equivalent Thicknesses. Periodica Polytechnica Civil Engineering, december. https://doi.org/10/gfkpqb
Tamás, P., Bojtos, A., Décsei-Paróczi, A. & Fekete, T. R. 2014: Végeselem módszerek. Budapest: BME MOGI.
Tóth, Cs. 2007: A teherbíróképesség meghatározásának ellentmondásai és lehetőségei. Közúti és Mélyépítési Szemle 57 (8): 13–20.
Tóth, Cs. & Tóth, J. 2008: „Útpályaszerkezetek roncsolásmentes diagnosztikai lehetőségei”. Közúti és Mélyépítési Szemle 58 (5–6): 10–15.
Van Blommestein & Willem, B. 2016: Experimentally Determined Material Parameters for Temperature Prediction of an Automobile Tire Using Finite Element Analysis. PhD Thesis, Stellenbosch, South Africa: Stellenbosch University.
Van Vuuren, J. D. 1974: Relationship Between Tire Inflation Pressure and Mean Tire Contact Pressure. Transportation Research Record 523: 76–87.
Wang, H. 2011: Analysis of Tire-Pavement Interaction and Pavement Responses Using a Decoupled Modeling Approach. PhD Thesis, Urbana, Illinois: College of the University of Illinois.
Wang, W., Shan, Y., & Shugao, Z. 2013: Experimental Verification and Finite Element Modeling of Radial Truck Tire Under Static Loading. Journal of Reinforced Plastics and Composites 32 (7): 490–98. https://doi.org/10.1177/0731684412474998
Yazdandoost, F. & Saied, T. 2016: Finite Element Tyre Model for Antilock Braking System Study. International Journal of Vehicle Design 72 (3): 248–261.
Yoder, Eldon J. 1959. Principles of Pavement Design. New York: John Wiley and Sons, Inc.
Zhang, Z., Hongxun, F., Xuemeng, L., Xiaoxia, C., & Di, T. 2020: Comparative Analysis of Static and Dynamic Performance of Nonpneumatic Tire with Flexible Spoke Structure. Strojniški Vestnik – Journal of Mechanical Engineering 66 (7–8): 458–66. https://doi.org/10/ghcfjh
Zhou, H., Guolin, W., Yangmin, D., Jian, Y., Chen, L., & Jing, F. 2015: Effect of Friction Model and Tire Maneuvering on Tire-Pavement Contact Stress. Advances in Materials Science and Engineering 2015: 1–11. https://doi.org/10.1155/2015/632647
Zsichla, L. 1990: A mértékadó behajlás számítása mechanikai módszerrel. Közlekedésépítés- és mélyépítéstudományi szemle: a Közlekedéstudományi Egyesület lapja 40 (10): 370–75.
Erre a szövegre így hivatkozhat:
Király Tamás, Primusz Péter: A gumiabroncs és az útpályaszerkezet érintkezési kapcsolatának elemzése végeselem módszerrel, 2020, DOI: 10.36246/UL.2020.2.04
