https://doi.org/10.36246/UL.2021.1.01
2021; 9. évfolyam, 15. szám
Pdf: A fagyás és az olvadás hatása az útpályaszerkezetekre
Bevezetés
A környezeti jellemzők, mint a hőmérséklet, csapadék, légnedvesség, fagyás-olvadás ciklusok és a talajvíz mélysége jelentős hatással vannak az útburkolatok állapotára és élettartamára, ezért a pályaszerkezetek méretezésénél is fontos tényezőként vehetők figyelembe. Az időjárásnak való kitettség hatása a vékonyabb pályaszerkezeteknél erőteljesebb lehet, ezért különösen fontos a környezeti jellemzők alaposabb vizsgálata az alsóbbrendű vagy mezőgazdasági utaknál, az erdők feltáróhálózatánál, és az agro-erdészeti rendszerek kiszolgáló útjainál.
A klimatikus jellemzők változásában valószínűleg a szélsőséges időjárási események gyakoriságának növekedése várható. A legfontosabb befolyásoló események lehetnek a nagy intenzitású felhőszakadásszerű esőzések és ennek vízelvezetési problémái, a jelentős szélviharok, a nyári időszakokban fellépő hosszabb aszályos időszakok megjelenése, valamint a hőhullámok és a korai és a kései fagyok [1].
Tekintettel kell lenni az előbbiekben felsoroltak mellett a klimatikus jellemzők szezonális változékonyságára is, és a pályaszerkezetek méretezését javallott ezekhez a szezonális változásokhoz kapcsolni [11]. Az aszfalt rétegek hőmérsékletének változásai lényegesek, mert az aszfaltkeverékek modulusai nagyon érzékenyek a hőmérsékletváltozásra. A hajlékony pályaszerkezetek méretezésénél emellett az alsó rétegek (főként a földmű) talajnedvességének változásai a meghatározóak. A földmű moduluszok általában az optimális talajnedvességre és sűrűségre (tömörségre) vonatkoznak, de javarészt viszont az optimálistól eltérő jellemzőkre korrekciós faktorok szükségesek. Továbbá a fagyás olvadás jelensége és ennek ciklusai is igen jelentősen befolyásolják az alsó rétegek és a földmű teherbírását. Hiszen a fagyos periódusok alatt a földmű teherbírása nő, míg az olvadási periódusok alatt jelentősen csökken, tehát a fagyás mélységének és az egyes olvadási ciklusok egymásra következésének ismerete is egy fontos kérdés.
Az aszfaltburkolatú pályaszerkezetek tartósságának számításánál, az egyszerűen meghatározható és általában könnyen elérhető meteorológiai paraméterek közül, a hőmérséklet, ennek ingadozása és a csapadék a figyelembe vehető tényezők [2]. Az Útügyi Lapok c. folyóirat 13. lapszámában közölt: „A klimatikus jellemzők hatásai az útpályaszerkezetre” című kézirat dolgozta fel ennek a két paraméternek az általános változási tendenciáit Magyarországon, figyelembe véve a klímaváltozást [12]. A 14. lapszámban közölt A klimatikus jellemzők hatásai az útpályaszerkezetre: A pályaszerkezet hőmérsékletek számítása c. cikk a pályaszerkezet hőmérsékletek számításának lehetőségeivel foglalkozott [13]).
Jelen cikk pedig a fagyás és az olvadás útpályaszerkezetre gyakorolt hatásait elemzi.
Fagyás, olvadás általános hatásai
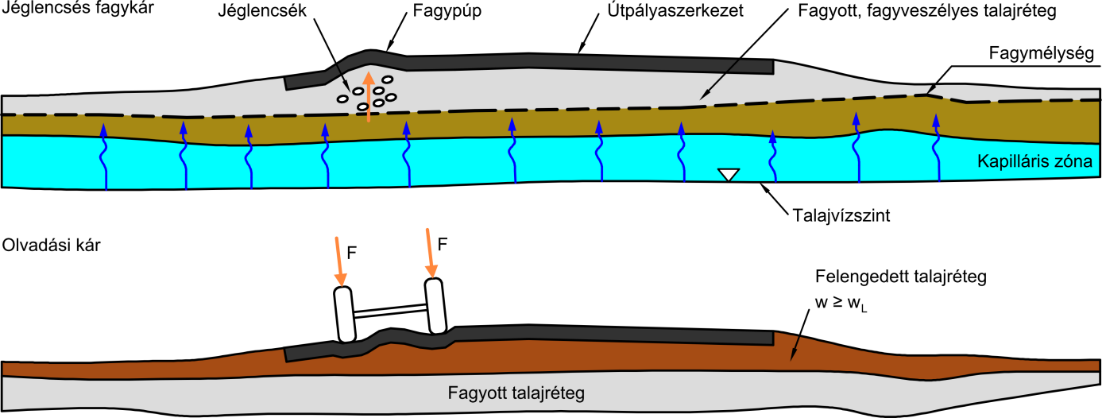
A fagyás, de különösen az azt követő olvadás következtében előálló talajnedvesség növekedés, valamint földmű teherbírás csökkenés veszélyes lehet a pályaszerkezetre. A hatásokat az 1. ábra szemlélteti.
 |
A következőben először a fagyás révén előálló fagykárt, majd a fagyok elmúltával bekövetkező olvadás és annak folyományaként bekövetkező olvadási kárt mutatjuk be.
Fagykár
A fagykár a megfagyott víz térfogat növekedésének következménye (az eredeti térfogat durván 1/9-ével nő szilárd halmazállapotban a jég térfogata, a cseppfolyós halmazállapotú és azonos tömegű vízhez képest). Hatását a pályaszerkezeti rétegekben és földműben is kifejti.
Bár az aszfaltburkolat repedésmentes állapotában érzéketlen a fagyra, viszont, ha hajszálrepedések jelennek meg a burkolatban, akkor azokon keresztül bejutó víz megfagyva meggyorsíthatja a rongálódási folyamatot. Ezt a rongálódási folyamatot elsősorban nem a fagyás indukálja, hanem pl. a „fáradás”, amelynek hatására a hajszálrepedések elsődlegesen képződnek.
Az alaprétegben akkor keletkezhet fagykár, ha maga az alaprétegnek felhasznált szemcsés anyag fagyveszélyes (1. táblázat). A cementstabilizált alapréteg fagyérzékenysége pedig abban mutatkozhat meg, hogy az alacsony cementadagolás esetében az széteshet.
| Érzékenység | Talajfajta | Finom részek [tömeg %] | Plasztikus index | |
| <0,02 mm | <0,1 mm | Ip[%] | ||
| Fagyálló | Homokos kavics | <10 | <25 | – |
| Kavicsos homok | ||||
| Homok | ||||
| Fagyérzékeny | Iszapos kavics | 10-15 | 25-40 | – |
| Iszapos homok | ||||
| Agyag | – | – | 15,1< | |
| Fagyveszélyes | Homokliszt | <10 | – | 1,0-5,0 |
| Iszapos homokliszt | 10< | 40-90 | 5,1-10,0 | |
| Iszap | – | – | 10,1-15,0 | |
Az előző táblázathoz kapcsolódóan mutatjuk be a 2. ábrát, amely az Agrotopográfiai térkép alapján a talajok fizikai féleségét prezentálja a fagyveszélyes talajok térbeli elhelyezkedésének szemléltetésére. Az 1. táblázat és a 2. ábra kategóriái teljes mértékben nem feleltethetőek meg egymásnak. A kapcsolatot a 2 mm alatti szemcsék, homok (0,05–2,0 mm), iszap (0,002–0,05 mm) és agyag (<0,002 mm) kategóriái közötti megoszlását figyelembevevő textúrára vonatkozó háromszögdiagram teremtheti meg [14]. Azok a talajok, amelyek dominánsan egy jellemző frakcióból állnak osztályozhatók homok, iszap és agyag fizikai féleségűként (ezek a háromszögdiagram sarkaiban találhatóak). A különböző szemcseméretekből közel azonos mennyiségű szemcsét tartalmazó talajok pedig az ú.n. vályog kategóriába sorolhatóak (háromszögdiagramm középpontja).
 |
A „fagykár” a megfelelően megválasztott és fagyállóságra bevizsgált anyagok alkalmazásával, a pályaszerkezet rétegeiben elkerülhető. A méretezés alapfeltétele, hogy a fagyállósági követelményeket kielégítsük, így ennek a méretezésre nincs hatása.
A földmű esetében viszont, az azt alkotó talajoknál megkülönböztethetünk „tömbfagyást” és „jéglencsés fagyást”.
A „tömbfagyás” a szemcsés talajok jellemzője, ahol a talaj pórusaiban megfagyó víz térfogat növekedése olyan típusú, hogy nem eredményezi a talaj számottevő térfogat növekedését.
A „jéglencsés fagyás” viszont a finomszemcsés talajokra jellemző, ahol kialakuló ún. fagyási gócok térfogat növekedést okoznak. A fagyási gócok megjelenése szívóhatással jár, hiszen az alacsonyabb hőmérséklet következtében a talajban lévő pára a melegebb helyről a hidegebb helyre (mint alacsonyabb páranyomású, tehát abszolút értelemben szárazabb helyre) áramlik. Az ide áramló nedvesség a fagypont alatti hőmérséklet miatt kifagy, tehát az ideáramló nedvesség ellenére sem növekszik a páranyomás, hanem alacsony szinten marad. Az előbbiek miatt a párafluxust fenntartó gradiens jelentős marad, ami így további nedvesség ide áramlását eredményezi. Igaz ez annak ellenére, hogy az alsó melegebb talajréteg fokozatosan szárad. A fagyási gócok tehát tovább növekednek, és ezáltal nő a jéglencsék térfogata. Végeredményképpen az ilyen fagyási gócok a felszínt több cm-el megemelhetik. Érdemes azt is megemlíteni, hogy a jéglencsés fagyás esetében (a nyomóerők miatt) a víz fagyáspontja lecsökken kb. -2 °C. Ennek eredményeképpen a jéglencsés fagyás határa nem a 0 °C-os izoterma szintjén van, hanem a hideg felszínhez közelebb [9].
A jéglencsés terepfelszín (vagy burkolatfelszín) emelkedés (ú.n. fagyemelkedés) tipikus fajtája a mi klímánkon ritka jelenség. A jéglencsék egyenletes eloszlása következtében viszont a finomszemcsés talajok esetében bizonyos fagyemelkedés jelentkezhet. Sőt előállhat a jelenség akkor is, amikor a klasszikusnak vett talajvízből származó nedvesség utánpótlódására nincs lehetőség [2].
A jéglencsés fagykár forgalomfüggetlen, így a forgalomra való méretezésnél nem, csak a méretezés kiindulásakor a fagyállósági követelmények teljesítésével veendő figyelembe [2].
A fagybehatolási mélység számítása
A fagynak a talajba való lehatolása a gyakorlati élet számos területét közelről érinti. Az útburkolatok állékonyságának érdekében a reálisan várható fagyveszély ellen valamilyen módon a tervezés során fel kell lépni. Ez a tervezés során méretezésként legtöbbször a mértékadó útépítési fagyhatár értékének (amely nagyjából a fagybehatolási mélységgel azonosnak vehető) meghatározását jelenti [9].
A fagybehatolási mélység alapján tervezhető a fagy elleni védekezés. A legnagyobb fagybehatolási mélység azonban nem önmagától a legalacsonyabb hőmérséklettől függ, hanem a fagytartam alatti napi középhőmérsékletektől és az ezekből számított hidegmennyiségtől.
A fagybehatolási mélység az a terepszinttől vertikálisan lefelé mért távolság, melyben az átfagyott talaj a még nem fagyott talajjal érintkezik [3]. Ez a mélységet tulajdonképpen a 0 °C-os izoterma adja meg. Ezt az izotermát a fagymélységet közrefogó mélységekhez tartozó talajhőmérsékleti adatokból lehet, pl. interpoláció útján meghatározni, bár a talajhőmérsékleti adatok csak korlátozott számban állnak rendelkezésre. Megoldásként szolgálhat az a nemzetközileg is validált, eredetileg [5] által levezetett összefüggés, amely szerint a fagybehatolási mélység a fagyási index négyzetgyökével arányos.
A fagyási index viszont léghőmérséklet adatok alapján számítható. Definíció szerint a hőösszeg görbén a fagytartam alatti maximum és minimum közötti különbség Celsiusnap-ban kifejezve. A hőösszeg görbe az értelmezés szerint valamely adott naptól kezdve a napi középhőmérsékletek összegének (Celsius nap) menetét megjelenítő diagram.
Más megfogalmazás szerint a fagyási index (a hidegmennyiség számértéke) a fagyperiódus alatti napok számának a Celsius fokban kifejezett átlaghőmérséklettel való szorzata foknapban kifejezve. A fagyási indexet tehát úgy számítjuk, hogy a negatív középhőmérsékletű napok középhőmérsékleteit összeadjuk, vesszük az abszolút értéküket és ebből asz összegből a pozitív középhőmérsékletű napok középhőmérsékletinek összegét levonjuk. A tervezés szempontjából a mértékadó a fagyási index az elmúlt 30 év 3 leghidegebb telén észlelt fagyási indexek átlaga (Boromisssza 1997). A fagyási indexet szemlélteti a 3. ábra.
 |
Később Shannon laboratóriumi körülmények között is igazolta a Breggen-féle összefüggést, a következő egyenlet segítségével:
\[ Z_{f}= k ⋅ F^{0,5} \]
Ahol:
Zf: a fagybehatolási mélység cm-ben;
F: a fagyási index Celsius nap-ban;
k: pedig egy állandó.
A k tényező Shannon által becsült értéke: k=3,8-ra, amely Európai szinten is elfogadott [3]. A számítások alapján Magyarország esetén hasonló a k tényező, átlagosan 3,7.
A fagybehatolási mélységeknél azonban ajánlatos azt is figyelembe venni, hogy a pályaszerkezet saját fizikai jellemzői (hővezető, hőtároló képesség, stb.) függvényében is módosítja a fagybehatolás mélységét.
Az előbbiek szerint tehát a talajokra általában megadott összefüggés nem valószínű, hogy az útburkolatok alatt is ugyanúgy érvényes. A fagybehatolási mélység egy svájci szabályozás szerint [16], amely a pályaszerkezet mélységét is figyelembe veszi a következőképpen számítható.
\[ Z_{pf}= 45 ⋅ F^{0,5}+ \frac{D}{2} \]
Ahol:
Zpf: a fagy behatolási mélység a pályaszerkezet alatt [mm];
F: a Fagyási index Celsiusnap-ban;
D: a pályaszerkezet vastagsága [mm].
Az utak pályaszerkezet alatti fagybehatolási mélységére vonatkozó összefüggés alapján az látszik, hogy a fagybehatolási mélység nagyobb a pályaszerkezet alatt általában, mint a zavartalan talajfelszín esetében. Ez egyrészt a fagyási index nagyobb szorzójából, másrészt az újabb (pályaszerkezet alatti fagyási mélységet számító) egyenletben megjelenő, a pályaszerkezet fele vastagságát figyelembevevő, összeadó-állandóból következik (ami a természetes talajra vonatkozó egyenletben nem jelent meg).
Fagyási indexek és fagybehatolási mélység alakulása Magyarországon
Budapest környékére vonatkozó a fagyási indexeket (mint jó országos átlagot képviselő hely) a 4. ábra mutatja. Az ábra alapján tetten érhető, hogy 1963/64 tele mértékadó volt ebből a szempontból, 320-as fagyási indexel (kb. 66 cm-es fagybehatolási mélységgel). Az 1980-óta eltelt időszakban a 2003/2004-es tél volt a legjelentősebb, bár ennek fagyási index már csak 181 volt (kb. 50 cm-es fagybehatolási mélységgel). A jövőre vonatkozóan, a REMO modell korrigált adati szerint, nem várható jelentős mértékű csökkenés a fagyási indexekben (4. ábra). Az elkövetkezendő 30-évre vonatkozóan a maximális fagyási index 190 Celsius nap, ami kb. 51 cm-es fagybehatolási mélységet jelent a talajokban.
 |
A következő 5. ábra megjelenített térkép az 1951-2014-es időszakra készült fagyási indexeket mutatja országos léptékben.
 |
Az 1951-2014-es időszakban a fagyási index területi átlaga Magyarországra 406 Celsius nap. A maximum, az Északi-Középhegység magasabb területein jellemző 685 Celsius nap, míg a minimum a DNY Dunántúlon található (286 Celsius nap). A fagyási indexek régiók szerinti eloszlását a 2. táblázat mutatja.
| Osztály | Min. | Max. | Átlag | Szórás |
| BK | 286 | 461 | 355 | 29,52 |
| D | 307 | 406 | 355 | 19,12 |
| DA | 313 | 453 | 399 | 35,63 |
| EA | 367 | 514 | 459 | 36,21 |
| EM | 360 | 685 | 489 | 68,29 |
| KD | 306 | 473 | 362 | 36,35 |
| NYD | 339 | 425 | 371 | 15,50 |
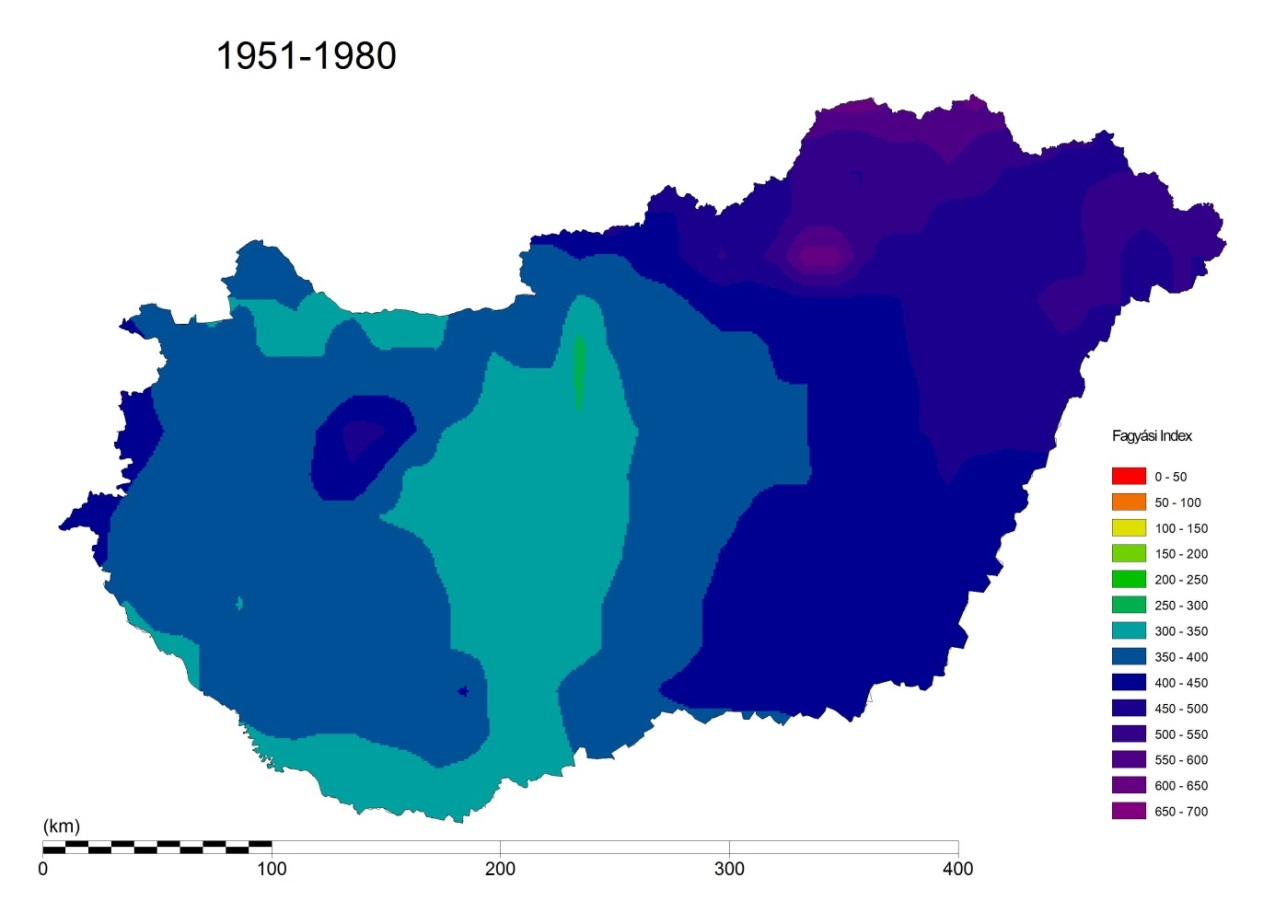
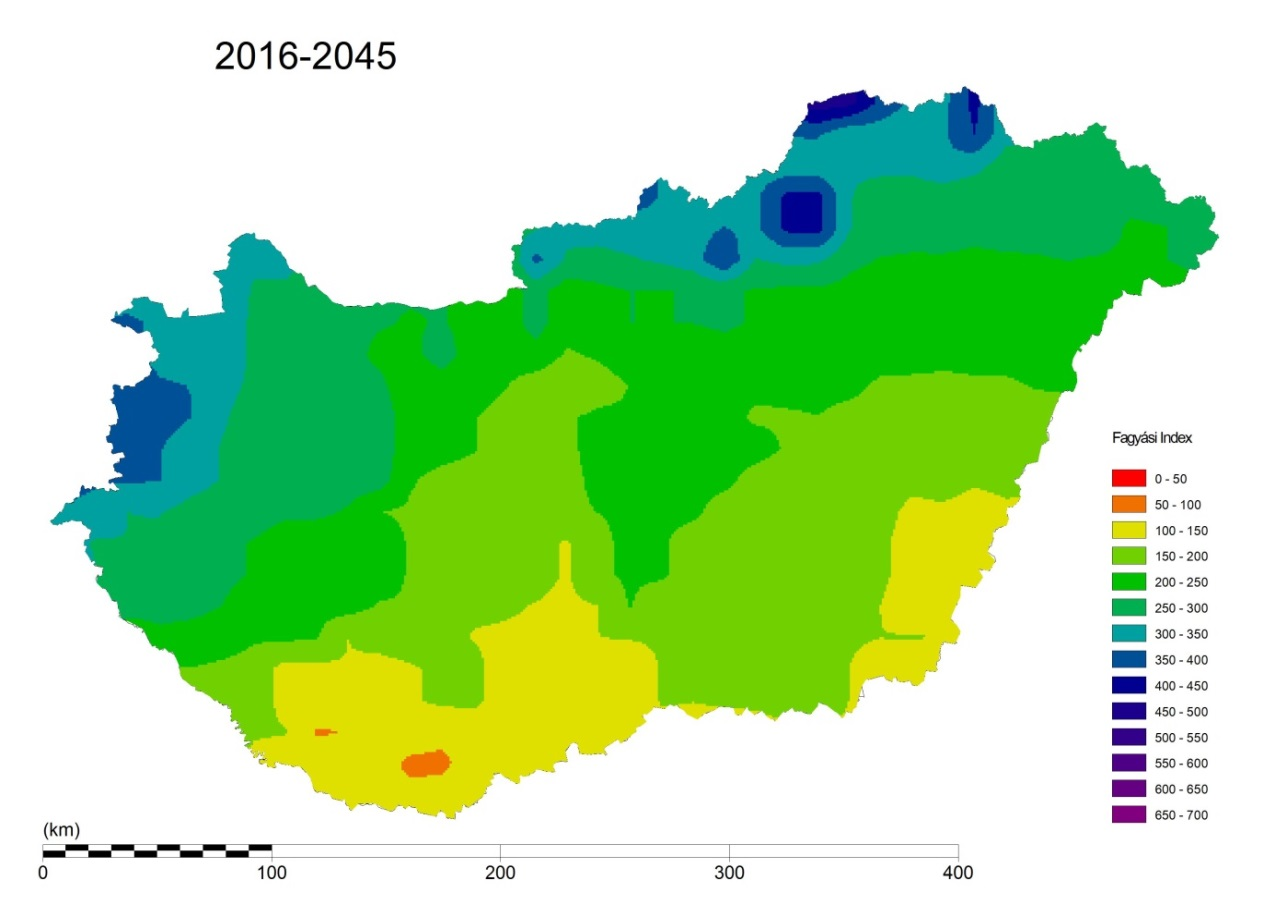
A fagyási indexek múltra, jelenre és jövőre vonatkozó értékei között jelentősebb eltérés lehetséges, ezért a klimatikusan vizsgált 30 éves időszakokra (1951-1980, 1981-2010 és 2016-2045) is elkészítettük a fagyási index értékeket. A fagyási index adatok térbeli eloszlását a 6., 7. illetve 8. ábrák, valamint a 4. 5. és 6. táblázatok mutatják.
 |
| Régió | Min. | Max. | Átlag | Szórás |
| BK | 287 | 416 | 354 | 28,18 |
| D | 310 | 405 | 356 | 18,43 |
| DA | 314 | 453 | 396 | 34,89 |
| EA | 369 | 515 | 458 | 37,89 |
| EM | 362 | 635 | 482 | 58,25 |
| KD | 306 | 473 | 364 | 33,44 |
| NYD | 340 | 460 | 373 | 19,03 |
 |
| Régió | Min | Max | Átlag | Szórás |
| BK | 141 | 309 | 211 | 36,95 |
| D | 119 | 216 | 165 | 18,34 |
| DA | 151 | 323 | 247 | 45,47 |
| EA | 234 | 383 | 325 | 32,57 |
| EM | 219 | 513 | 357 | 58,73 |
| KD | 141 | 263 | 182 | 25,61 |
| NYD | 122 | 220 | 167 | 12,28 |
A 6. ábra alapján megállapítható, hogy az 1951-80-as időszakban a fagyási indexek országos átlaga 404 Celsius nap (a szórása 60 körüli) 634-es maximummal az Északi Középhegységben és 287 körüli minimummal Budapesttől délre. Az 1981-2010-es időszakban a fagyási indexek országos területi átlaga már csak 245 Celsius nap (a térbeli szórás értéke 82) 512-es maximummal és 119-es minimum értékkel. Az előbbiek szerint a két egymást követő 30-éves periódusban a fagyási indexek országos átlaga közel 160-as értékkel csökkent, a térbeli szóródás azonban jelentősen nőtt.
A jövőre vonatkozóan a 8. ábra, és 6. táblázat alapján a 2016-45-ös periódusban, a REMO modell előrejelzései szerint, a fagyási indexek országosan kismértékben tovább csökkennek 245 Celsius napról 221-es értékre. A maximum (480 Celsius nap) és a minimum (87 Celsius nap) érték is tovább csökken. Az országos eloszlás a klímamodell szerint kissé módosul, de ezt fenntartásokkal ajánlatos kezelni, mivel a klimatikus előrejelzések becslések és nem valós méréseknek. Az előrejelzések szerint térbeli szóródás feltehetően kismértékben csökken majd.
 |
| Régió | Min. | Max. | Átlag | Szórás |
| BK | 154 | 364 | 218 | 30,96 |
| D | 87 | 251 | 161 | 36,44 |
| DA | 103 | 221 | 158 | 24,08 |
| EA | 140 | 288 | 217 | 34,20 |
| EM | 216 | 480 | 303 | 52,20 |
| KD | 163 | 304 | 234 | 39,03 |
| NYD | 198 | 381 | 299 | 36,53 |
Fagyásbehatolási mélység
Bár a fagybehatolási mélység függ az adott talaj hővezetési és hőkapacitási értékeitől is, mégis lehetőség van, hogy körülbelüli becslést tegyünk a természetes talajokban, valamint az útpályaszerkezetek alatt jellemző értékekre az egyes időszakokban.
A továbbiakban példaként nézzük idősorszerűen Budapest környékére vonatkozóan a fagybehatolási mélység alakulását a természetes talajokban és az útpályaszerkezet alatt, a korábbi általános képlet szerint (9. ábra).
A számítások során a pályaszerkezet vastagságára 50 cm-es értéket vettünk figyelembe.
A Budapesti fagyási index értékekkel 1963/64 telére vonatkozóan a 320-as fagyási index 105 cm-es fagybehatolási mélységgel jellemezhető a pályaszerkezet alatt (ez 39 cm-el több, mint a természetes talajra számított összefüggés). Az 1980-óta eltelt időszakban a 2003/2004-es tél volt a legkomolyabb, ennek fagyási indexe 181 volt, ez 86 cm-es fagybehatolási mélységgel jellemezhető a pályaszerkezet alatt (ami 36 cm-el több, mint a természetes talajra számított összefüggés). A fagybehatolási mélység az elkövetkező 30-évben (2016-2045) a Remo klímamodell adati szerint nem változik szignifikánsan (190-es fagyási index mellett a maximális fagybehatolási mélység a pályaszerkezet alatt 87 cm).
 |
A fagybehatolási mélységekre vonatkozó múltbeli trend szerint, Budapest környékére vonatkozóan, a természetes talajokban jellemző fagybehatolási mélység jellemzően évtizedenként közel 2,3 cm-el, míg a pályaszerkezet alatt közel 2,9 cm-el csökkent.
A fagybehatolási mélység esetében nem készítettünk ábrákat, hiszen az adatok csak tájékoztató jellegűek, mivel nem veszik figyelembe az egyes talajok, ill. pályaszerkezet típusok fizikai jellemzőit (pl. fizikai féleség, nedvesség stb.). A talajok hővezetési és hőtároló képességére vonatkozóan szolgáljanak iránymutatásként [6] adati (7.táblázat), aminek segítségével lehetőség nyílik a helyi jellemzők figyelembevételére.
| Anyagtulajdonság | Kavics/ Homok |
Vályog (Iszap) | Agyag | Aszfalt-beton |
| Modulus [MPa] | 138 | 103 | 69 | 150-21000* |
| Sűrűség [kg/m3] | 1922 | 1442 | 1682 | 2211 |
| Nedvességtartalom [%], természetes száraz állapot (hervadáspont) | 3 | 10 | 20 | 0 |
| Hővezető képesség, fagyott [W/m·hr·Celsius] | 1,2 | 0,5 | 0,3 | 1,5 |
| Hővezető képesség, nem fagyott [W/m·hr·Celsius] |
1,7 | 0,8 | 0,7 | 1,5 |
| Fajhő fagyott [kJ/m3·Celsius] | 1489 | 1328 | 1006 | 1878 |
| Fajhő nem fagyott [kJ/m3·Celsius] | 1610 | 1630 | 1676 | 1878 |
| Látens hő [MJ/m3] | 19,3 | 48,3 | 33,5 | 0,0 |
Olvadási kár
Az olvadási kár a talajfagy felengedése idején a talaj túlzott elnedvesedése és ennek következtében bekövetkező teherbírás csökkenése miatt következik be (1. ábra). Az olvadási kár különösen abban az esetben veszélyes, amikor a felengedett talajréteg alatt még fagyott, így tehát közel vízzáró talajréteg található. Ha ilyen időszakban csapadékvíz jut a pályaszerkezet alá, az a fagyott talajréteg miatt elszivárogni nem tud. Az előbbiek miatt folyós, teherbírás nélküli vagy csökkent teherbíró képességű alapréteg keletkezhet. A legutoljára felengedő talajréteg az irodalom [2] alapján durván a fagyási mélység 2/3-ában van. Ha a pályaszerkezeten nincs forgalom, az olvadási kár nem jelentkezik, a forgalom függvényében viszont igen jelentős mértékű lehet.
Az alapréteg tél végi – tavasz eleji teherbírás csökkenése akkor is bekövetkezhet, ha a külső vízutánpótlás lehetősége (pl. a csapadékból) nem áll fenn. A korábban taglaltak szerint ugyanis a fagyott, vagyis hidegebb zónában a talaj pórusaiban lévő vízpára kicsapódik. Az előbbi páramozgás általában alulról fölfelé, a fagyott zóna felé irányul és az alsóbb rétegek természetes víztartalmából származik. Alul tehát, ha nincs jelen a talajvízszint a kapilláris vízforgalom számára elérhető mélységben, kiszáradás, a felső zónában pedig elnedvesedés indul meg.
Az olvadási károk ellen alapvetően kétféleképpen lehet védekezni:
- az erre veszélyes talaj (6. táblázat) kizárásával, kiváltásával az alaprétegben;
- a vízutánpótlás kizárásával.
Mivel a vízutánpótlás teljes kizárása a pályaszerkezet teljes élettartama alatt általában nem lehetséges, ezért mind a fagyás mind az olvadás ellen fagyálló talaj, azaz fagyvédő réteg beépítésével lehet hatékonyan védekezni.
Olvadási és fagyási kár veszélye
Az olvadási és fagykár ellen tehát akkor kell védekezni, ha a talaj fagyveszélyes, illetve fagyérzékeny.
Az olvadási kár veszélye a Boromissza-féle mértezési előírás szerint akkor áll fenn, ha a következő feltételek teljesülnek egyidejűleg:
- a földmű felső 50cm-es rétegének talaja fagyveszélyes, vagy fagyérzékeny
- az utolsó 15 év becsült maximális talajvízszintje a pályaszintet legalább 2,0m-re megközelítette,
- a felszíni víz behatolásának megakadályozása céljából vízzáró padkaburkolat, vagy a forgalmi sáv külső szélétől számítva minimum 50-50 cm-el túlnyúló vízzáró alapréteg nem készült [2].
A károk megelőzése céljából a következő megoldások lehetségesek:
Fagyálló anyagból olyan vastag védőréteget kell beépíteni, hogy a következő egyenlet teljesüljön.
\[ h_{v}= F-∑h_{i}·f_{i} \]
Ahol:
hv: a fagyálló védőréteg vastagsága [cm];
hi: az egyes rétegek vastagsága [cm];
fi: az egyes pályaszerkezeti rétegek 28. táblázat szerinti komplex anyagai jellemzője, amely figyelembe veszi a pályaszerkezeti réteg hőszigetelő képességét, hajlítószilárdsági tulajdonságait és vízzáróságát;
F: az éghajlati körülményeket jellemző állandó (7. táblázat).
| Fagy- határ- zóna |
Tengerszint feletti magasság és 10. ábra | A,B és C terhelési osztály | D, E és K terhelési osztály | ||
| Fagyérzékeny talaj | Fagyveszélyes talaj | Fagyérzékeny talaj | Fagyveszélyes talaj | ||
| I. | A 10. ábra szerinti I. zóna | 40 | 50 | 60 | 70 |
| II. | Az 10. ábra szerinti II. zóna és az I.-es zóna 250m-500 m közötti területei | 50 | 60 | 70 | 80 |
| III. | 500 m feletti területek | 60 | 70 | 80 | 90 |
| A pályaszerkezeti réteg megnevezése | f |
| Zúzottkő alapok | 1,0 |
| Mechanikai stabilizáció | 1,0 |
| Cementtel stabilizált talaj | 1,1 |
| Aszfaltmakadám | 1,2 |
| Cementtel stabilizált homokos kavics | 1,3 |
| Soványbeton alap | 1,4 |
| Betonburkolat | 1,5 |
| Aszfaltbeton, öntött aszfalt | 1,5 |
| Meleg bitumenes alap | 1,5 |
 |
A 10. ábra és a fagyási indexek területi eloszlást mutató korábbi, 5.6.7. valamint 8. ábra összehasonlításából látható, hogy a Boromissza által közölt útépítési fagyhatárzónákat elkülönítő vonal az 1951-80-as időszak 500-as fagyási index értékének megfelelő. Az 500-as fagyási indexet jelképező érték kb. 83 cm-es fagybehatolási mélységgel jellemezhető a természetes talajoknál és kb. 126 cm-es fagyási mélységgel az utak pályaszerkezete alatt. Az 1981-2010 közötti időszakban ez az 500-as fagyási indexel jelzett fagyhatárzóna már csak a Bükk fennsíkon, valamint a Zemplén és Aggteleki karszt magasabb részein jelentkezik, a jövőben pedig már sehol nem lesz jellemző hazánkban. Az előbbiek szerint érdemes átgondolni a 7. táblázat jellemző pályaszerkezet vastagságait és a megfelelő mértékben csökkenteni azokat. A jövőben a korábbi (1951-1980) 500-as fagyási határ földrajzi környezete inkább a 250-es fagyási indexel (kb. 56 cm-es fagybehatolási mélység a természetes talajoknál és kb. 96 cm-es fagyási mélységgel az utak pályaszerkezete alatt) lesz jellemezhető.
Olvadási kárt indukáló talajnedvesség változás
A fagybehatolási mélység ismerete mellett fontos a fagyott talajrétegek részleges vagy teljes felengedése, felolvadása esetén, a földműben jelentkező teherbírás csökkenés. A jelenség a magas talajnedvesség növekedése vagy másként fogalmazva a földmű víztartalmának (a pórusokban lévő víz pórusnyomásának) egy határon túli növekedése formájában jelentkezik és a méretezés szempontjából számszerűen pl. a földmű modulus csökkenésében jelentkezik.
A talajnedvességek meghatározása egy Thornthwaite-féle [15] havi vízmérleg modellel történt. A modellszámítás a felső, kb. 1m es talajréteg nedvességkészletét mutatja egy relatív skálán, amely tulajdonképpen a szántóföldi vízkapacitás és a hervadásponti víztartalom közötti tartományban számít. Az előbbi ú.n. talajnedvesség érték tehát a kapilláris pórusok telítettségére utaló szám. Ha értéke zérushoz közeli, akkor a talaj (a növényi vízfelvétel szempontjából) teljesen száraznak tekinthető, ha 100 körüli az értéke, akkor pedig már a bármilyen plusz többletvíz a gravitációs pórusokat kezdi telíteni.
Az ország egészét tekintve a tavaszi időszakban átlagosan 49%-os a kapilláris pórusok telítettsége, ami 100% és 27 % minimális és maximális érték között oszlik el, átlagosan 11,8-es területi szóródással. A régiók szerinti megoszlást az 9. táblázat mutatja.
| Régió | Min (%) | Max (%) | Átlag (%) | Szórás |
| Dunántúl (D) | 30 | 57 | 41 | 6,64 |
| Budapest és környéke (BK) | 27 | 86 | 46 | 12,19 |
| Dél-Alföld (EA) | 28 | 59 | 46 | 7,04 |
| Észak-Magyarország (EM) | 42 | 100 | 60 | 13,74 |
| Nyugat-Dunántúl (NYD) | 31 | 72 | 45 | 9,44 |
| Közép-Dunántúl (KD) | 30 | 78 | 47 | 12,35 |
| Észak-Alföld (EA) | 42 | 73 | 55 | 9,12 |
A szántóföldi vízkapacitás közeli értékekkel rendelkező területek a magasabb talajnedvességűek, tehát a földmű teherbíró képessége szempontjából veszélyeztetettebbek a tavaszi időszakban. Az előbbiek szerint az Északi Középhegység, ill. az Alföld ÉK-i része, valamint a Nyugat-Dunántúl határközeli területei, itt is elsősorban az Őrség és a D-NY zalai területek. Ezek a kritikus helyek a téli csapadékösszeget mutató térképen is. Ott a legkedvezőtlenebb a helyzet, ahol a magas tavaszi talajnedvesség kedvezőtlen talajfizikai féleségekkel iszapos-agyagos talajok is kombinálódik.
A talajnedvességek alakulása a Thorntwaite-féle havi vízmérleg modell alapján a múltban a 11. táblázat alapján jellemezhető.
Az ország egészét tekintve a tavaszi időszakban egy átlagosan 71%-os a kapilláris pórusok telítettsége (az 1981-2010-es időszakban 49%), ami 100% és 54 % minimális és maximális érték között oszlik el (az 1981-2010-es időszakban 100% és 27%), átlagosan 11,4-es területi szóródással (az 1981-2010: 11,8%). A régiók szerinti megoszlást a 11. táblázat mutatja.
| Régió | Min. [%] | Max. [%] | Átlag [%] | Szórás |
| D | 61 | 98 | 78 | 9,70 |
| BK | 54 | 98 | 64 | 10,45 |
| DA | 55 | 77 | 62 | 3,70 |
| EM | 57 | 100 | 79 | 13,42 |
| NYD | 61 | 100 | 75 | 12,23 |
| KD | 59 | 100 | 70 | 8,00 |
| EA | 57 | 88 | 68 | 8,01 |
A szántóföldi vízkapacitás közeli értékekkel rendelkező területek a magasabb talajnedvességűek, tehát a földmű teherbíró képessége szempontjából veszélyeztetettebbek. Az előbbiek szerint a hegyvidéki részeken kívül az alföld ÉK-i része, valamint a Dél-Nyugat-Dunántúl területei, az Őrség, a Mura és a Dráva menti területek.
A múlthoz (1951-80) képest tehát a tavaszi kapilláris telítettséget jellemző talajnedvesség készlet jelentősen, mintegy 22%-al csökkent. A csökkenés a Dél-Dunántúlon, a Dunántúl keleti területeinek középső részén, valamint a Kisalföld középső és dél-nyugati részén a legjelentősebb.
A talajnedvességek alakulását a jövőben a 11. táblázat alapján jellemezhető.
Az ország egészét tekintve a tavaszi időszakban egy átlagosan 34%-os a kapilláris pórusok telítettsége (az 1981-2010-es időszakban 49%), ami 82% és 7 % maximális és minimális érték között oszlik el (az 1981-2010-es időszakban 100% és 27%), átlagosan 12,2-es területi szóródással (az 1981-2010-es időszakban 11,8). A régiók szerinti megoszlást a 11. táblázat mutatja.
| Régió | Min. [%] | Max. [%] | Átlag [%] | Szórás |
| BK | 10 | 66 | 28 | 11,85 |
| D | 10 | 46 | 27 | 9,03 |
| DA | 9 | 49 | 34 | 9,92 |
| EA | 16 | 65 | 38 | 9,79 |
| EM | 7 | 82 | 40 | 15,57 |
| KD | 11 | 62 | 30 | 12,63 |
| NYD | 17 | 60 | 35 | 10,73 |
A szántóföldi vízkapacitás közeli értékekkel rendelkező területek a magasabb talajnedvességűek, tehát a földmű teherbíró képessége szempontjából veszélyeztetettebbek. A 11. táblázat adatai szerint a jövőben szinte kizárólag az Északi-Középhegység magasabb területei lesznek tavasszal átlagosan magasabb talajnedvességűek.
A jelenhez (1980-2010) képest tehát a tavaszi kapilláris telítettséget jellemző talajnedvesség-készlet jelentős, mintegy 15%-os csökkenése feltételezhető majd.
A földmű modulusra vonatkozóan több irodalom dolgoz ki összefüggéseket, általában a talajok fizikai jellemzői alapján: a három fő irányban a nyomófeszültségek, a plasztikus index, talajalkotók (homok, iszap, agyag arányai), folyási határ, valamint az aktuális talajnedvesség. A CBR mérésekkel átlagában jól korreláltatható a földmű modulusza, de sajnos ez is talajtípusfüggő. A szemcsés és a kohéziós talajokra általában külön egyenletek kidolgozottak [10]. Például szolgáljon [7] által kidolgozott összefüggés:
Szemcsés talajok:
\[ \log_{M_{R}}=0,52300225·w+0,544·\log_{(σ)}+0,173·SM+0,197·GR \]
Ahol:
Mr: a földmű modulusa [ksi, 1MPa=0,15ksi];
w: víztartalom [%];
σ: összes feszültség [psi, 1 psi = 6,89 kPa];
SM: iszap faktor (ha a talaj iszap fizikai féleségű SM=1, különben 0);
GR: kavics faktor (ha a talaj kavicsos (kavics, kavicsos iszap, kavicsos agyag) akkor GM=1, különben 0).
Kohéziós talajok:
\[ M_{R}= 37,431-0,4566·PI-0,6179·w-0,1424·P_{200}+0,1791·σ_{3}-0,3248·σ_{d}+36,722·CH+17,097·MH \]
Ahol a korábban nem szereplő paramétereken felül:
PI : plasztikus index [%];
P200: a 200-as (0.075 mm) szitán keresztülhulló anyagmennyiség [%];
σ3: z irányú főfeszültség[psi];
σd: hatékony feszültség[psi];
CH: 1 a nagy plaszticitású agyagokra, különben 0 (iszap, iszapos agyag, alacsony plaszticitású agyag);
MH: 1 a nagy plaszticitású iszapokra, különben 0 (nagy plaszticitású agyag, iszap, iszapos agyag).
Ha a talajnedvesség adat nem áll rendelkezésünkre, akkor a földmű modulus magasabb talajnedvesség következtében előálló korrekciójára (olvadás miatt csökkenő voltára) egy az adott talajfizikai jellemzőknek megfelelő korrekciós faktor (R) megadását javasolja a nemzetközi szakirodalom. A R faktor az anyag fagyás-olvasással szembeni érzékenységét mutatja és [16] szerint a következőképpen kalkulálható:
\[ R= 1-(1-R_{0})·exp(A·U_{t}) \]
Ahol:
R0: a korrekciós faktor (R) minimális értéke a mértékadó (legkedvezőtlenebb) tavaszi olvadási időszakban;
Ut: az eltelt hetek száma a mértékadó olvadási időszak óta;
A: a változás rohamosságának a mértékét mutató negatív konstans, amely a földmű szezonális kiszáradási folyamat gyorsaságát mutatja.
[4] a földmű modulusokra is vonatkozó havi értékek eloszlását mutató táblázatot közöl. A táblázatban a földműmodulusokra a téli hónapokban (december-február) egy 80 MPa-os, a tavaszi hónapokban márciusban-áprilisban egy 30 MPa-os, májusban pedig egy 40 MPa-os értéket ad meg (a többi hónap földműmodulusa 50 MPa értékkel föltüntetett). A táblázat kidolgozása valószínűleg az 1951-80-as időszak meteorológiai adatait alapul véve történt, azóta viszont, ahogy említettük, a tavaszi talajnedvességek csökkenése következett be mintegy 22%-os relatív értékkel. Ez a jelenség és a jövőben prognosztizálható további csökkenés (a REMO modell előrejelzése alapján további 15%-os átlagos csökkenés valószínűsíthető tavasszal) következtében a földmű teherbírásának növekedése várható a tavaszi hónapokban, azon belül is különösen a tavasz végén.
A tél végén a hőmérsékletek növekedése (közel 2 °C-os a havi átlaghőmérséklet növekedés februárban, a növekedés az 1951-80-as időszak és a 2015-2045-ös előre jelzett periódus között jelentkezett) és a 0 °C alatti hőmérsékletű napok számának csökkenése (körülbelül 4,4 napos csökkenés februárban 11,8-ról 7,4 napra az 1951-80-as időszak és a 2015-2045-ös előrejelzett periódus között) erőteljes. Az előbbiek alapján valószínűsíthető, hogy az olvadási kárral leginkább veszélyeztetett időszak korábbra tolódik és a február hónapra egy lényegesen alacsonyabb földmű modulus valószínűsíthető. A májusra viszont a szárazodás és magasabb hőmérsékletek miatt valószínűleg növekvő földmű modulusz lesz jellemző. Az előbbiek szerint a [4] által közölt táblázat a következők szerint módosulhat (9. táblázat).
| Hónapok | Földmű modulus [4] [MPa] |
Földmű modulusok a jövőben (lehetséges változás) [MPa] |
| Jan. | 80 | 80 |
| Febr. | 80 | 30 |
| Már. | 30 | 30 |
| Ápr. | 30 | 40 |
| Máj. | 40 | 50 |
| Jún. | 50 | 50 |
| Júl. | 50 | 50 |
| Aug. | 50 | 50 |
| Szept. | 50 | 50 |
| Okt. | 50 | 50 |
| Nov. | 50 | 50 |
| Dec. | 80 | 80 |
A földmű modulusára vonatkozóan a Svéd szabályozás a tavaszi olvadásos, kritikus időszakra a nyári érték 35%-át adja, míg a Dán szabályozás a 60%-át. Az olvadást követő tavaszi periódusra, már kevésbé átáztatott földműre vonatkozóan, a nyári modulus százalékában a Svéd előírások szerint 50%, míg a Dán szabályozás révén 80%-os érték vehető figyelembe [8]. A hazai előírás a Dán arányokhoz áll közelebb.
Összefoglalás
A környezeti jellemzők, mint a hőmérséklet, csapadék, légnedvesség, fagyás-olvadás ciklusok és a talajvíz mélysége jelentős hatással vannak az útburkolatok állapotára, élettartamára, ezért a pályaszerkezetek méretezésénél is fontos tényezőként vehetők figyelembe.
A klímaváltozás a megváltozó környezeti jellemzők miatt a pályaszerkezetek tervezési paramétereinek, esetleg magának a tervezési elveknek a módosítását indukálja.
A fagyási indexek országos átlaga tekintetében az 1951-80-as időszakban 404 Celsius nap, az 1981-2010-es időszakban a fagyási indexek országos területi átlaga már csak 245 Celsius nap, tehát a két egymást követő 30-éves periódusban a fagyási indexek országos átlaga közel 160-as értékkel csökkent, bár a térbeli szóródás azonban jelentősen nőtt. A REMO modell előrejelzései szerint, a jövőre vonatkozóan a fagyási indexek országosan kismértékben tovább csökkennek (245 Celsius napról) 221-es értékre. Az országos eloszlás a klímamodell szerint kissé módosul.
A tél végén a hőmérsékletek növekedése (közel 2 °C-os a havi átlaghőmérséklet növekedés februárban, az 1951-80-as és a 2015-2045-ös között) és a 0 °C alatti hőmérsékletű napok számának csökkenése (~ 4,4 napos csökkenés februárban 1951-80-as és a 2015-2045-ös időszak között) erőteljes.
1951-80-as időszakhoz képest a tavaszi talajnedvességek csökkenése következett be, mintegy 22%-os relatív értékkel. A jövőben további csökkenés várható (a REMO modell: ~15%-os átlagos csökkenés valószínűsíthető tavasszal)
Az előbbiek alapján valószínűsíthető, hogy az olvadási kárral leginkább veszélyeztetett időszak korábbra tolódik és a február hónapra egy lényegesen alacsonyabb földmű modulus, májusra azonban a szárazodás és magasabb hőmérsékletek miatt valószínűleg növekvő földmű modulusz lesz jellemző.
Köszönetnyilvánítás:
A publikáció az Agrárminisztérium támogatásával készült.
Irodalomjegyzék
[1]: Bartholy, J., Bozó L. & Haszpra L. (szerk.) 2011: Klímaváltozás – 2011. Klímaszcenáriók a Kárpát–medence térségére. Magyar Tudományos Akadémia és az Eötvös Loránd Tudományegyetem Meteorológiai Tanszéke, Budapest, p. 281.
[2]: Boromissza, T. 1997: Méretezési Praktikum, Aszfaltburkolatú útpályaszerkezetek méretezési gyakorlata, Közúti közlekedési füzetek 16, Közlekedési, Hírközlési és Vízügyi Minisztérium, Budapest, p. 82.
[3]: Boromissza, T., Detre, Gy., Lazányi, I. & Szalai, S. 2007: Az útépítési fagyhatárzónák pontosítása. Közúti és mélyépítési szemle, 6. szám: 16-21.
[4]: Fi, I., Boncs, P., Pethő, L. & Tóth, Cs. 2012: Útburkolatok méretezése. Terc Kft. ISBN 978 963 9968 349, p. 457.
[5]: Berggren, W. P. (1943): Prediction of temperature-distribution in frozen soils. Transactions – American Geophysical Union 24(3): 71-77. https://doi.org/10.1029/TR024i003p00071
[6]: Bosscher, P. J., Jong, D. T. and Benson, C. H. (1998): International Conference on Cold Regions Engineering, 9th, Duluth, MN, Sep. 27-30, 1998. Proceedings. Cold regions impact on civil works. Edited by D.E. Newcomb. Publisher: Reston, VA, American Society of Civil Engineers (ASCE). United States.: 731-747.
[7]: Carmichael, R.F. III & Stuart, E. 1985: Predicting Resilient Modulus: A Study to Determine the Mechanical Properties of Subgrade Soils. ”Transportation Research Record TRR 1043, Transportation Research Board, National Research Council, Washington, DC.
[8]: Dawson, A. (2009). Water in Road Structures (Movement, Drainage and Effects), Spring Science + Business Media B.V. 2009. ISBN: 978-1-4020-8561-1, p. 436.
[9]: Gáspár, L. (1959): Az útépítési fagyhatár megállapítása léghőmérsékleti adatokból. Mélyépítéstudományi szemle. IX. évf. 10. szám: 472-480.
[10]: George, K. P. (2004): Prediction of resilient modulus from soil index properties. Final Report. University of Missisipi. p. 72.
[11]: Gupta, A. 2014: A review of Environmental Factors on Flexible Pavement Modelling, Modern Traffic and Transportation Engineering Research, vol:3 iss:1 pg:14-20
[12]: Gribovszki, Z., Kalicz, P., Herceg, A. & Primusz, P. 2020: A klimatikus jellemzők hatásai az útpályaszerkezetre, Útügyi Lapok, https://doi.org/10.36246/UL.2020.1.01
[13]: Herceg, A., Primusz, P., Kalicz, P. & Gribovszki, Z. 2020: A klimatikus jellemzők hatásai az útpályaszerkezetre: A pályaszerkezet hőmérsékletek számítása, Útügyi Lapok, https://doi.org/10.36246/UL.2020.2.02
[14]: Radcliffe, D. E., Simunek, J. 2010: Soil Physics with HYDRUS: Modeling and Applications, CRC Press, ISBN 9781420073805, p. 388
[15]: Thornthwaite, C.W. and Mather, J.R. (1955): The waterbalance. Philadelphia, PA: Drexel Institue of technology, climatological laboratory publication 8.
[16]: Ullidtz, P. (1998): Modelling Flexible Pavement Response and Performance. Tech Univ. of Denmark Polyteknisk, ISBN: 978-8750208051, p. 205.
Erre a szövegre így hivatkozhat:
Kalicz Péter, Herceg András, Primusz Péter, Gribovszki Zoltán: A fagyás és az olvadás hatása az útpályaszerkezetekre, 2021, DOI: 10.36246/UL.2021.1.01
