https://doi.org/10.36246/UL.2022.1.04
2022; 10. évfolyam, 16. szám
Pdf: Új építésű aszfaltrétegek vastagságának és tömörségének meghatározása földradarral
Bevezetés
A roncsolásmentes vizsgálatok fő előnye abban rejlik, hogy gyorsan és zavarásmentesen lehet nagymennyiségű mérést úgy végrehajtani, hogy közben nem okozunk kárt a vizsgált szerkezetben. Ez utóbbi tulajdonság főleg új építésű útpályaszerkezeteknél különösen fontos, ahol nem lehet „szétfúrni” a beépített rétegeket az építési minőség ellenőrzése érdekében sem. Az útpályaszerkezet diagnosztikában alkalmazható roncsolásmentes vizsgálatok részletes áttekintése megtalálható [1] munkájában, valamint magyar nyelven [2] összefoglalóját javasoljuk átolvasásra. A cikkben felsorolt eszközök és eljárások közül mi most csak a földradar (Ground Penetrating Radar, GPR) méréstechnológiával foglalkozunk. Az eljárás nem csak leromlott állapotú útszakaszok kiértékeléséhez, hanem újépítésű szakaszok minőségellenőrzéséhez is kiválóan felhasználható (sőt, inkább erre használják leginkább), mivel képes a forgalom zavarása nélkül nagymennyiségű folytonos térbeli adathalmazt összegyűjteni. A folytonos mérés azért különösen fontos és hasznos, mivel a lokális pontokban (a 25–50 vagy akár 500–1000 m-es szelvénytávolságokban) meghatározott szerkezeti adatok térbeli kiterjesztése egyáltalán nem egyértelmű és könnyű feladat, nem is beszélve azok „valós” átlagos értékének meghatározásáról. A hagyományos mintavételezési eljárásokkal a lokális hibák kimutathatatlanok, pedig azok nagyrésze még az építés közben kijavítható lenne, ha elég gyorsan kap visszajelzést a kivitelező. Cikkünkben ezért a földradar alkalmazhatóságát vizsgáljuk a minőség-ellenőrzés területén.
Elméleti háttér
A földradar műszer jellemzően egy adó és egy vevő antennából, egy adatgyűjtő és vezérlő egységből, egy mérőkerékből és opcionálisan egy GPS-ből áll. A földradar adó része nagyfrekvenciás elektromágneses impulzusok sorozatát bocsátja ki. A hullámok a vizsgált közegben részben elnyelődnek, részben visszaverődnek [3]. A visszaérkező jelet (feszültséget) a vevő egység veszi az idő függvényében, digitalizálja és az adatrögzítő egység tárolja [4]. A radarjel terjedése a vizsgált közeg elektromos és mágneses tulajdonságaitól függ. Ezek közül a két legjellemzőbb, a dielektromos állandó (permittivitás) és a vezetőképesség (konduktancia). Az aszfaltrétegek in-situ relatív dielektromos állandóját megkapjuk a felületi visszaverődés (Surface Reflection, SR) módszerét alkalmazva [5]. A felületi visszaverődésen (reflexión) alapuló módszer azt használja ki, hogy a visszavert jel amplitúdója annál nagyobb, minél nagyobb a kontraszt a réteghatár két oldalán található anyag fizikai, elektromágneses tulajdonságaiban. A reflexiós együttható (R) – elhanyagolva a vezetőképességet – az alábbi képlettel számítható [6]:
\[ R=\frac{Visszaverődő hullám amplitudója}{Beeső hullám amplitudója} = \frac{\sqrt{ε_{1}}-\sqrt{ε-{2}}}{\sqrt{ε_{1}}+\sqrt{ε-{2}}} \]
ahol \(ε_{1} \) és \(ε_{2} \) az egymást követő rétegek dielektromos állandói. Az útpályaszerkezetre beeső hullám amplitúdóját ( \(A_{p} \) ) megkapjuk, ha egy rendkívül reflektív rézlemezt helyezünk a GPR antenna alá, ami tökéletesen visszasugározza a vevő felé a kibocsájtott jelet. A rézlemezt eltávolítva az antenna alól, és egy újabb mérést végrehajtva megkapjuk a kopórétegről visszaverődő hullám ( \(A_{0} \) ) amplitúdóját. Felhasználva ezeket az adatokat és figyelembevéve, hogy a levegő dielektromos állandója 1, az (1) egyenlet átrendezésével megkapjuk a keresett \(ε_{r} \) összefüggését:
\[ ε_{r}= [\frac{1+(A_{0}/A_{p})} {1-(A_{0}/A_{p})} ]^2 \]
ahol \(ε_{r} \) a felső aszfaltréteg dielektromos állandója, \(A_{0} \) az aszfaltréteg felületéről visszaverődő hullám amplitúdója, \(A_{p} \) pedig a rézlemezről visszaverődő hullám amplitúdója. A relatív \(ε_{r} \) dielektromos állandó ismeretében pedig már lehetőség nyílik egy adott réteg vastagságának kiszámítására:
\[ h_{i}=\frac{cΔt}{2\sqrt{ε_{r}}} \]
ahol c a fénysebesség (0,30 m/ns), \(A_{t} \) az \(A_{0} \) és \(A_{p} \) amplitúdók közötti kétirányú futási idő, és \(ε_{r} \) az anyag relatív dielektromos állandója. Így a radarmérés időtengelye mélységmetszetté alakítható. Amennyiben viszont ismert a \(h_{i} \) rétegvastagság (pl. fúrás által) akkor az \(ε_{r} \) dielektromos állandó határozható meg igen pontosan a (3) egyenletből.
Az útpályaszerkezetet felépítő rétegek dielektromos állandójára vonatkozóan vannak irodalmi adatok (aszfalt: 4–8; beton: 9–11), amelyek alkalmazásával könnyen, fúrómagmintavétel nélkül kiszámíthatjuk a rétegvastagságokat. A módszer nehézsége, hogy a dielektromos állandó az útépítési anyagoknál változó lehet, amire a nedvességtartalom, az ásványi összetétel, a hőmérséklet, a tömörség és a mérőfrekvencia egyaránt hatást gyakorol. Ez azzal magyarázható, hogy az útépítésben használt anyagok (talaj, zúzottkő, aszfalt, beton stb.) kémiai szempontból háromfázisú diszperz rendszerek, amikben a folyadék- és gázfázis aránya az időjárási tényezőktől nagymértékben függ. Ennek köszönhetően viszont a földradar mérések nem csak a rétegvastagságok meghatározására alkalmasak, hanem az aszfaltkeverékek testsűrűségének és szabadhézag-tartalmának megbecslésére, a földműanyagok tömörségének és nedvességtartalmának monitorozására, valamint az úthibák pl. repedések detektálásra is [7] [8] [9] [10]. További hasznos részletek olvashatóak az útpályaszerkezetek földradarral történő roncsolásmentes vizsgálati lehetőségeiről [11], valamint [12] magyarnyelvű cikkében.
Saarenketo (1997) [13] volt az egyik első kutató Európában, aki földradart használt az aszfalt-pályaszerkezetek sűrűségének mérésére. Kutatásai szintén azon az elven alapultak, hogy a pályaszerkezet dielektromos állandója feltételezhetően, az összetevőinek dielektromos állandóinak a függvénye. Ezért az összetevők (fázisalkotók) térfogatarányaiban bekövetkező változások kimutathatóak a teljes pályaszerkezet dielektromos állandójának mérésével.
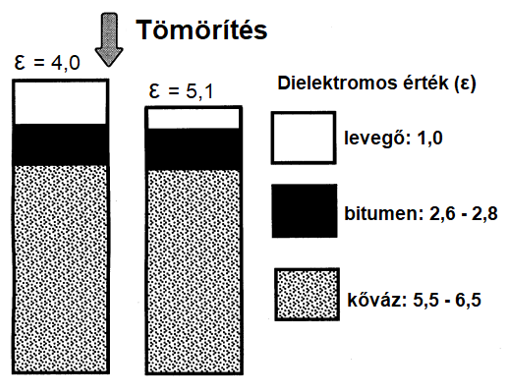
Az aszfaltkeverék összetevői közé tartozik a bitumen, az ásványi adalékanyag, a levegő és esetlegesen a víz (lásd 1. ábra). A bitumen dielektromos állandója általában 2,6 és 2,8 közötti tartományba esik, a zúzott száraz aggregátumok állandói 5,5 és 6,5 között változnak, a levegőé pedig 1. Bár a víz dielektromos állandója függ annak kémiai értelemben vett kötöttségi fokától, kijelenthető, hogy a víznek az új pályaszerkezet dielektromos állandójának mérésére nincs érzékelhető hatása.
 |
Laboratóriumi vizsgálatokkal korrelációs kapcsolatot kerestek a finn útügyi kutatók a száraz aszfaltkeverék dielektromos állandója és annak testsűrűsége között. A finn kutatások arra a következtetésre mutattak, hogy az útburkolat dielektromos állandója és annak szabadhézag-tartalma ( \(V_{A} \) ) között exponenciális kapcsolat van:
\[ V_{A}(\%)=a\cdot e^{-bε_{AC}} \]
ahol \( ε_{AC} \) az aszfaltburkolat dielektromos állandója (GPR antennarendszerrel meghatározható), a és b kalibrációs együtthatók, amelyek a keverék típusától függenek, és a helyszíni mérés közben vett magmintából meghatározhatóak. Különböző utakról gyűjtött GPR adatok bizonyították, hogy a dielektromos állandó értékének csökkenése sűrűségproblémákat jelez (lásd 1. ábra). A tanulmány által kimutatott legjelentősebb tény, hogy a GPR óriási lehetőségeket kínál a helyi problémák monitorozásában [14].
Anyag és módszer
A földradar méréstechnika lehetőségeit a minőségellenőrzés területen egy délalföldi lakóutca 220–240 m hosszú kísérleti útszakaszán vizsgáltuk meg. Méréseinket elsősorban a beépített aszfaltrétegek előírt vastagságának és azok szabadhézag-tartalmának ellenőrzésére kívántuk felhasználni.
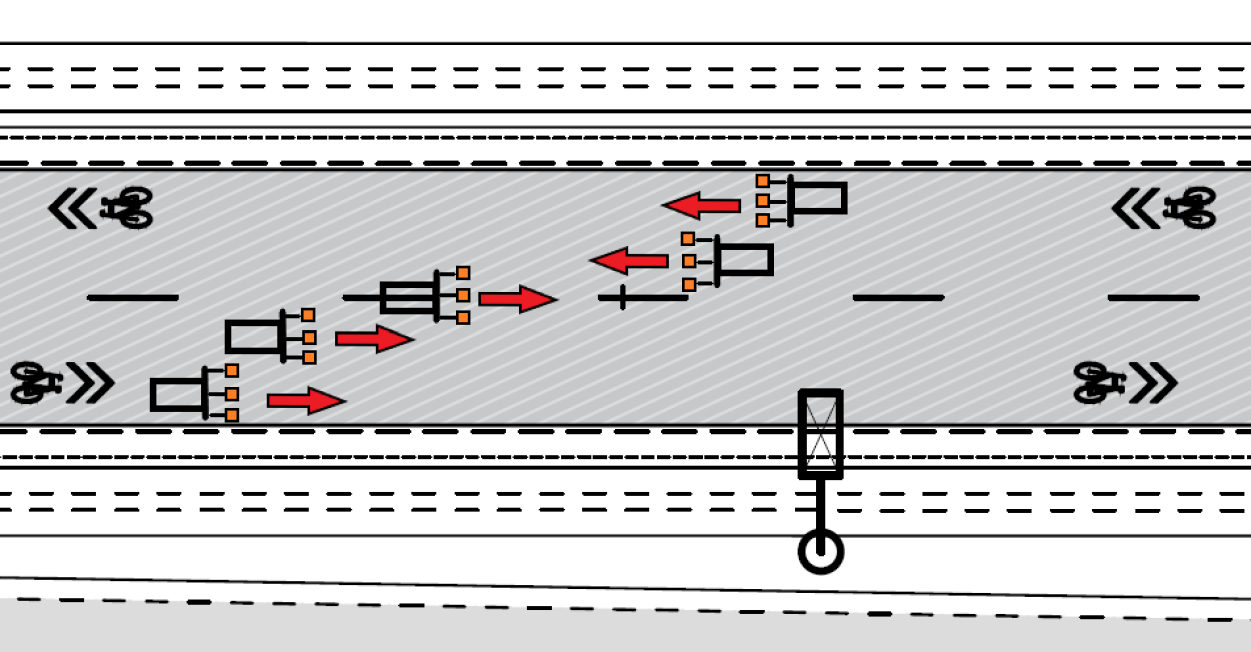
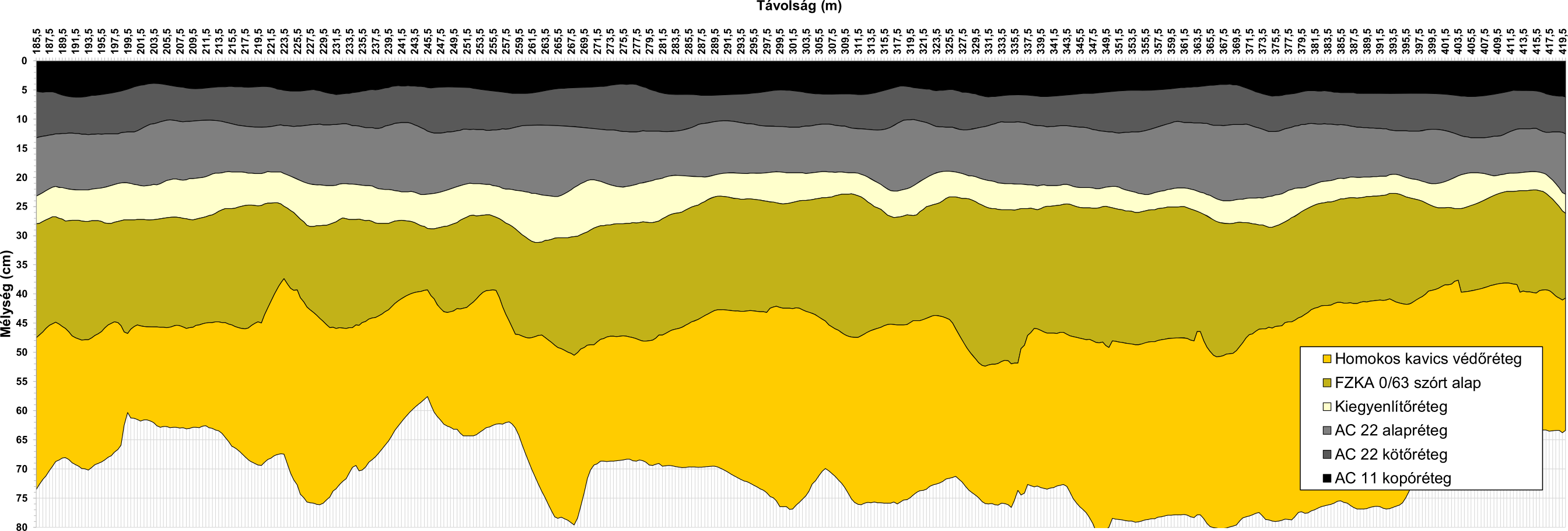
A kutatáshoz a földradar mérőrendszert a RODEN Mérnöki Iroda biztosította. A GSSI gyártmányú 1 GHz és 2 GHz frekvenciájú levegőcsatolt antennák a hordozó gépkocsi mögött 1,5 méterre, a burkolat felszíne felett pedig kb. 450 mm-re helyezkedtek el. Az antennák pontos elrendezését a 2. ábra mutatja be. A terepi mérés 16 km/h sebességgel, és méterenként 50 db letapogatással történt. A nyers adatokat a nagysebességű SIR-30 többcsatornás adatgyűjtő és vezérlőrendszer rögzítette. A begyűjtött adatok közül tanulmányunkban most csak a jobb felbontású 2 GHz-es antennák RADAN szoftverrel feldolgozott eredményeit értékeljük. Ennek hátterében az áll, hogy az FZKA rétegre került 3–4 cm vastagságú kiékelő/kiegyenlítő szemcsés réteget folytonosan csak a 2 GHz-es antennák által észlelt szelvényeken tudtuk azonosítani. A RADAN7 szoftverből kiexportált rétegvastagságokat végül Microsoft Excel programmal halmozott terület diagramokon ábrázoltuk.
A beépített aszfaltrétegeket nem csak a levegőcsatolt antennákkal, hanem a PaveScan RDM 2.0 (második generációs) roncsolásmentes aszfaltsűrűség-értékelő mérőberendezéssel is megvizsgáltuk (3. ábra). A PaveScan berendezés alapvetően a vizsgált aszfaltkeverék dielektromos tulajdonságait méri és abból következtet a testsűrűségre. A készülék 3 darab egymástól tetszőleges (de maximum 1,1 m) távolságra elhelyezhető 2 GHz középfrekvenciájú levegőkapcsolt antennával (érzékelővel) van felszerelve az útpálya felületének minél teljesebb lefedése érdekében.
 |
 |
A szenzorok 30 cm magasságban vannak rögzítve a felszín felett. A szenzorok a felületi visszaverődés (SR) módszer alapján, automatikusan kiszámítják az aszfalt adott pontjára vonatkozó dielektromos állandót. A mérőműszer méterenként 40 letapogatást végez, amelynek köszönhetően nagy felbontású dielektromos állandó meghatározást tesz lehetővé. A mérést megelőzi az úgynevezett levegő kalibráció, melynek célja a háttérzajok eltávolítása, valamint a fémlemez kalibráció, melynek célja az aszfalt felszínének, valamint a fémlemezről visszavert hullám amplitúdójának detektálása.
A mérőműszerek rövid bemutatásából kiemeljük, hogy mind a két földradar 2 GHz középfrekvenciájú levegőkapcsolt antennákkal dolgozik, amik a felszín felett közel azonos 30–45 cm magasságban helyezkednek el. Ezért a két mérőberendezés által meghatározott dielektromos állandókat jelentősen sem a mérési magasság, sem a mérési frekvenciákból származó különbségek nem terhelhetik.
A kutatásban vizsgált két forgalmi sávos lakóutca tervezett útpályaszerkezetének felépítése az alábbi volt:
- 4,0 cm AC 11 kopó (F) réteg
- 7,0 cm AC 22 kötő (F) réteg
- 8,0 cm AC 22 alap (F) réteg
- 20,0 cm FZKA 0/63 szórt alap (3-4 cm vastag 0/22 szemcsés réteggel eltakarva)
- 20,0 cm homokos kavics védőréteg
 |
 |
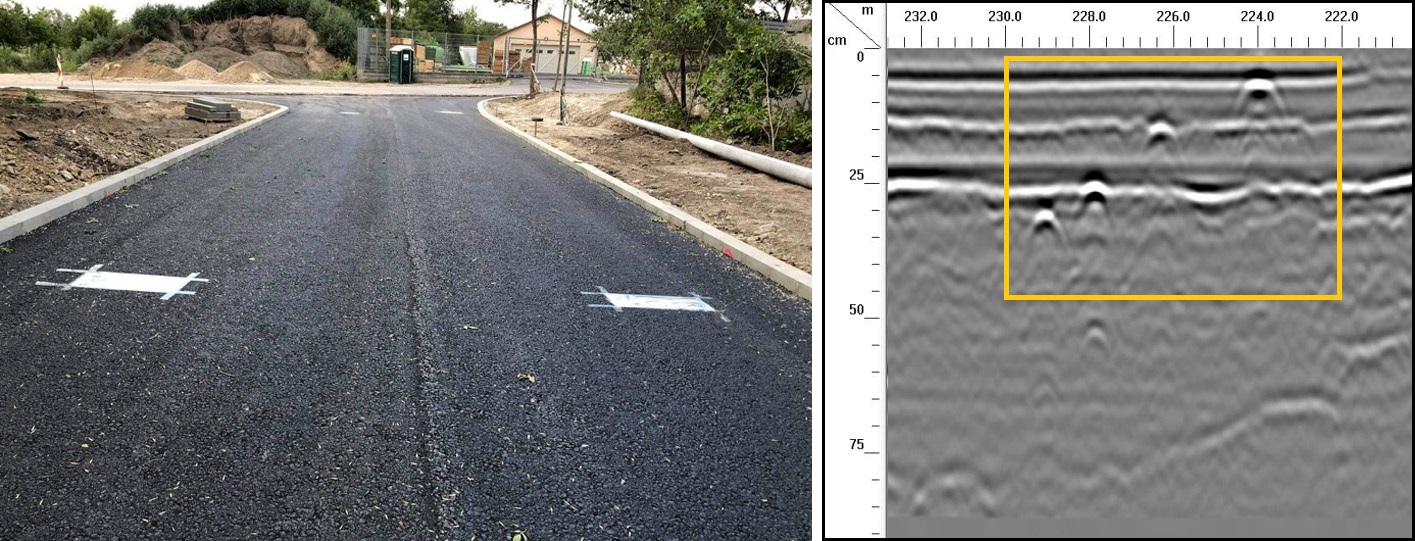
A kísérleti útszakasz pályaszerkezetének építése közben lehetőség nyílt 20 méterenként az aszfaltrétegek alá egymástól 1 méterrel eltolva antipólusokat elhelyezni (4. ábra). Erre a célra a könnyen beszerezhető háztartási alumínium fóliát választottuk, de a 2-3 mm vastag fémlemez is megfelelő eredményt ad. Az antipólusok a GPR által kibocsájtott hullámenergiát teljesen visszaverik, ezért az aszfaltréteg aljának pontos helye parabola alakú visszaverődés képében azonosítható a radarszelvényen. Megjegyzendő, hogy ezek az alumínium fóliák a gyakorlatban nem szükségesek a GPR mérésekhez, csak a kutatási eredmények validálására szokás használni.
Mind a két földradar berendezéssel három mérést hajtottunk végre a teljes kísérleti útszakaszon. Az első (1) mérés az AC 22 aszfalt alapréteg beépítése után, a második (2) mérés az AC 22 aszfalt kötőréteg beépítése után, végül a harmadik (3) mérés az AC 11 aszfalt kopóréteg beépítés után történt meg. A rétegenkénti méréseknek köszönhetően valamennyi aszfaltréteg dielektromos állandójáról információt kaptunk. A teljes útpálya lefedése érdekében sávonként két mérés történt, egy a sávszélen (a szélső szenzor padka mellett), egy pedig a sávközépen (a szélső szenzor az úttengely mellett). A részletesebb adatgyűjtés érdekében a mérések kiegészültek egy úttengely menti felméréssel is (5. ábra).
 |
A vizsgált útpályaszerkezet rétegeinek vastagságát meghatároztuk a GSSI gyártmányú 2 GHz frekvenciájú levegőcsatolt antennák által gyűjtött adatokból, mivel itt elsősorban a beépített antipólusokra támaszkodtunk (4. ábra). A beépített aszfaltrétegek testsűrűségének megbecsléséhez viszont már az erre a célra kifejlesztett PaveScan RDM 2.0 eredményekből indultunk ki. A földradar mérések validálásához fúrt magmintákat használtunk. Az aszfalt alapréteg beépítését követően 3–3, az aszfalt kötőréteg beépítését követően pedig újabb 3–3 fúrómag került kivételre a jobb és bal sávban egymástól kb. ~70 méterenként (6. ábra). A fúrt magminták rétegvastagságát az MSZ EN 12697-36:2003 szabvány szerint, míg a testsűrűségeket az MSZ EN 12697-6:2012 szabvány szerint megállapítottuk. A térfogati jellemzők keveréktervezési kritériumként, vagy a keveréknek az útpályaszerkezetbe való terítése és tömörítése utáni kiértékelési paramétereként használatos. A beépített aszfaltkeverékek legfontosabb jellemzői az alábbiak voltak: AC 11 kopóréteg \(G_{mm} \) hézagmentes testsűrűsége 2436 kg/m3. AC 22 alap- és kötőréteg hézagmentes \(G_{mm} \) testsűrűsége 2572 kg/m3 és 2580 kg/m3. A kötőanyag súly szerinti aránya 4,1%, relatív sűrűsége 1050 kg/m3, a felhasznált kőváz hézagmentes testsűrűsége pedig 2759 kg/m3.
A kutatás további részében korrelációt kerestünk a mért \(ε_{AC} \) dielektromos állandó és az aszfaltréteg \(G_{mb} \) testsűrűsége között. Mivel a szabadhézag-tartalom a következő összefüggés szerint számítandó:
\[ V_{A}(\%) = 100\cdot \frac{G_{mm}-G_{mb}}{G_{mm}} \]
a (4)-es számú képlet exponenciális függvénye jó választásnak tűnt erre a célra, mivel ha ismerjük \(V_{A} \)-t, akkor a fenti képletből \(G_{mb} \) értéke könnyen kifejezhető:
\[ G_{mb} = (1-V_{A})\cdot G_{mm} \]
A modell paraméterinek meghatározásához az eredeti (4) exponenciális függvényt a következő formában alkalmaztuk:
\[ V_{A}(\%)=α\cdot e^{-βε_{AC}}+ε \]
ahol \(V_{A} \) a szabadhézag, \(ε_{AC} \) az aszfalt dielektromos állandója, és β a keresett modellparaméterek, ϵ pedig a hibatag. A hibatag megjelenése a modellben azt jelenti, hogy a dielektrikumon kívül más tényezők is befolyásolhatják a szabadhézag-tartalom előrejelzésének pontosságát, amelyek közé tartozhat a modell hibája, az anyagok és a környezet, például a hőmérséklet vagy a nedvességtartalom változékonysága.
 |
A modell kalibrálásához fúrómag mintavételre, vagy az adott aszfaltkeverékből előállított gyratoros próbatestekre van szükség [15]. A vizsgált lakóutca AC 22 alap- és kötőrétegéből sikerült fúrt mintákat venni, viszont ezek az AC 11 kopóréteg esetében nem álltak rendelkezésünkre. Ezért a kalibrációhoz a BME laboratóriumában gyratoros próbatesteket készítettünk, majd meghatároztuk ezek testsűrűségét és dielektromos állandóját a PaveScan RDM 2.0 készülékkel (7. ábra). A helyszíni és laboratóriumi adatok már lehetővé tették, hogy a (7)-es képlet modellparamétereit az átlagos négyzethiba gyökének (Root Mean Square Error, RMSE) minimalizálásával meghatározzuk, majd a dielektromos állandókat átszámítsuk testsűrűségre vagy szabadhézag-tartalomra. A terepi mérések után a PaveScan RDM 2.0 eszközből 0,5 méterenként kiexportáltuk a dielektromos állandó értékeket a sávszegélytől az úttengely felé haladva a következő szenzorpozíciókban: 2,9 m; 2,3 m; 1,7 m; 1,3 m; 0,7 m; 0,6 m; 0,1 m és 0 m. Az így előállított térbeli dielektromos állandókból végül a Surfer 14 szoftverrel készítettünk szintvonalas sűrűségtérképeket.
Eredmények és megvitatásuk
A következőkben bemutatjuk és megvitatjuk a vizsgált lakóutca aszfalt rétegein végrehajtott földradarméréseink eredményeit, tapasztalatait. Elemzésünket a vastagságméréssel kezdjük, mivel ez az egyik legkézzelfoghatóbb minőségi paraméter, aminek teljesülnie kell. Vastagság minősítési jellemzőnél az előírt érték a tervezett vastagság. Az aszfaltrétegek vastagságának előírt és megfelelőségi határai részben a mintaszámától függenek (e-ÚT 06.03.21/M1). Ha a mintaszám ≥ 10 db, akkor az átlagos rétegvastagság legalább érje el az Előírt érték–6%-ot. Az átlag vastagság megfelelősségi határértéke ekkor az Előírt érték–12% a hivatkozott szabályozás szövege szerint.
Az első (1) AC 22 aszfalt alaprétegen történt mérések eredményei azt mutatták, hogy a radarszelvényeken valamennyi beépített réteg egyértelműen elkülönült egymástól. A nagy pontosságú rétegazonosítást segítették a kiegyenlítő- és az aszfalt alapréteg alatt elhelyezett antipólusok, melyek egymástól 1 méterrel eltolt hiperbolák formájában megjelentek a radarképen (4. ábra jobb oldala). Az előzetes elvárásoknak megfelelően a szemcsés kiegyenlítő réteg és az AC 22 aszfalt alapréteg vastagsága a hossz-szelvények mentén nem változik jelentősen (a vastagságadatok szórása ±1 cm), így ezen réteghatárok közel egyenes lefutásúak. Az AC22 aszfalt alapréteg előírt (8 cm) vastagságához képest a földradar +6,3%-os eltérést mutatott ki.
 |
| # | Rétegrend | Tervezett vastagság (cm) | CH2 (2GHz) | CH4 (2GHz) | ||||||
| Átlag (cm) | Szórás (cm) | N (db) | Eltérés (%) | Átlag (cm) | Szórás (cm) | N (db) | Eltérés (%) | |||
| 1 | AC 22 alap (F) | 8 | 8,5 | 0,98 | 461 | −6,3 | 8,5 | 1,08 | 464 | 6,2 |
| Kiegyenlítő réteg | 4 | 3,9 | 0,98 | 409 | +1,3 | 4,0 | 1,04 | 335 | 0,2 | |
| FZKA 0/63 szórt alap | 20 | 19,2 | 3,19 | 266 | +4,1 | 20,0 | 2,92 | 140 | 0,1 | |
| Homokos kavics vr. | 20 | 23,4 | 5,58 | 281 | −17,1 | 23,0 | 4,40 | 161 | 15,0 | |
| 2 | AC 22 kötő (F) | 7 | 6,4 | 1,15 | 462 | +8,1 | 6,5 | 0,98 | 470 | 7,3 |
| AC 22 alap (F) | 8 | 9,1 | 1,09 | 446 | −13,5 | 9,6 | 1,13 | 448 | 20,2 | |
| Kiegyenlítő réteg | 4 | 4,0 | 1,07 | 378 | +0,3 | 4,4 | 1,41 | 418 | 10,1 | |
| FZKA 0/63 szórt alap | 20 | 19,1 | 3,45 | 315 | +4,3 | 18,4 | 3,37 | 325 | 7,9 | |
| Homokos kavics vr. | 20 | 21,6 | 6,22 | 368 | −8,2 | 23,9 | 4,85 | 340 | 19,7 | |
| 3 | AC 11 kopó (F) | 4 | 4,8 | 0,70 | 479 | −18,9 | 5,2 | 0,70 | 479 | 30,8 |
| AC 22 kötő (F) | 7 | 6,5 | 0,84 | 479 | +7,2 | 6,3 | 0,97 | 447 | 10,1 | |
| AC 22 alap (F) | 8 | 9,0 | 1,43 | 479 | −13,1 | 9,6 | 1,67 | 447 | 19,5 | |
| Kiegyenlítő réteg | 4 | 4,6 | 1,27 | 439 | −14,9 | 5,0 | 1,58 | 467 | 24,9 | |
| FZKA 0/63 szórt alap | 20 | 17,0 | 2,69 | 284 | +15,0 | 19,0 | 3,36 | 292 | 4,8 | |
| Homokos kavics vr. | 20 | 25,0 | 7,89 | 275 | −25,1 | 26,4 | 5,83 | 301 | 31,9 | |
Az FZKA 0/63 szórt alap és a homokos kavics védőréteg esetén már jóval magasabb a vastagságadatok szórása (±3–5 cm), és így a rétegek lefutása is változatosabb.
A második (2) AC 22 aszfalt kötőrétegen történt mérések eredményei nagymértékben hasonlítottak az elsőhöz (1). Az AC 22 aszfalt alap- és kötőréteg vastagsága a hossz-szelvények mentén nem változik jelentősen (a vastagságadatok szórása ±1 cm), így ezen réteghatárok közel egyenes lefutásúak voltak. Az AC 22 aszfalt kötőréteg vastagsága az előírt 7 cm-től −7,7%-ban eltért. A földradar viszont az AC 22 aszfalt alapréteg vastagságára már +17%-os eltérést mutatott ki a tervezett vastagsághoz képest, ami magasabb, mint az első (1) méréskor kimutatott +6,3%-os érték.
A harmadik (3) utolsó mérés az AC 11 aszfalt kopórétegen történt, és az eddigiekhez hasonlóan a radarszelvényeken valamennyi beépített réteg egyértelműen elkülönült egymástól (8. ábra). Az AC 11 aszfalt kopó- és AC 22 kötőréteg vastagsága a hossz-szelvények mentén nem változik jelentősen (a vastagságadatok szórása ±0,8 cm), így ezen réteghatárok közel egyenes lefutásúak. Az AC 22 aszfalt alapréteg lefutása is egyenletes, de már magasabb ±1,5 cm-es szórás jellemzi az átlagos vastagságot. Az AC 11 aszfalt kopóréteg 4 cm-es előírt vastagságához képest a földradar átlagosan 5 cm-es vastagságot becsült, ami +25%-os eltérést jelent. Az AC 22 aszfalt kötőréteg eltérés −8,6% míg az AC 22 aszfalt alaprétegé +16,3% volt ezen felmérés szerint.
Az 1. táblázat alapján jól látható, hogy a három eltérő időpontban végrehajtott földradar felmérések, minden rétegre háromféle átlagos rétegvastagságot határoztak meg. A földradar vastagságmérés eredményeinek validálásához ezért a jobb és a bal sávból 3–3 fúrómag mintavétel történt a kötőréteg beépítését követően. A kopóréteg beépítése után nem történt már a teljes aszfaltvastagságot feltáró fúrómag mintavétel, csak 1 db magot fúrtak a bal sávból, amely kizárólag a kopóréteget tartalmazta. Ennek következtében a kopórétegen történt GPR mérések érvényesítéséhez a kötőrétegből vett 6 db fúrómag vastagságadatait és a fent említett 1 db fúrómag mélységadatát tudtuk felhasználni. Ezek után a három aszfaltréteg georadar felmérések alapján meghatározott vastagságának a fúrómagokon azonosított rétegvastagságokkal történő összehasonlítását a 2. táblázat tartalmazza.
Az eredményeket elemezve megállapítható, hogy a georadarral becsült AC22 aszfalt alapréteg vastagságát a fúrómagokhoz viszonyítva az első (1) mérésből átlagosan 1,4%; a másodikból (2) mérésből 1,9%; a harmadik (3) mérésből számolva pedig 6,5% hiba terhelte. Az AC 22 kötőréteg vastagságát a második (2) mérésből átlagosan 3,2%-os; a harmadikból (3) pedig 8,1%-os hibával lehetett meghatározni. Az AC 11 kopóréteg vastagságmérésének átlaghibája az 1 db feltárás alapján 2–8,5% közé tehető. A harmadik (3) kopórétegen történt felmérés eredményeiből számított átlagos eltérések nagyobbak, mint a kötő és alaprétegen történt mérések esetében kapott eltérések. Ennek hátterében a nedvesebb mérési körülmények állhatnak, mivel a kivitelező a burkolat mielőbbi forgalomhelyezhetősége érdekében – a mérést közvetlenül megelőzően – locsolta a kopóréteget és a kopórétegbe, illetve a felületre jutó víz befolyásolta a dielektromos állandó értékét.
Mindent figyelembe véve elmondható, hogy a tervezett vastagsági értékek kontroljaként a georadaros rétegvastagság meghatározás pontossága eléri a fúrásokkal történő ellenőrzés megbízhatóságát.
| # | Szelvény | Réteg | Sáv | CH2 (cm) | CH4 (cm) | Fúrás (cm) | CH2 Hiba (%) | CH4 Hiba (%) |
| 1 | 260 | AC 22 alap (F) | Jobb | 8,89 | 8,97 | 8,85 | 0,5 | 1,4 |
| 300 | AC 22 alap (F) | Jobb | 8,20 | 8,25 | 8,30 | 1,2 | 0,6 | |
| 370 | AC 22 alap (F) | Jobb | 8,78 | 8,84 | 8,95 | 1,9 | 1,2 | |
| 260 | AC 22 alap (F) | Bal | 7,98 | 8,04 | 8,10 | 1,5 | 0,7 | |
| 300 | AC 22 alap (F) | Bal | 7,64 | 7,87 | 7,70 | 0,8 | 2,2 | |
| 370 | AC 22 alap (F) | Bal | 7,31 | 7,66 | 7,50 | 2,5 | 2,1 | |
| 2 | 260 | AC 22 alap (F) | Jobb | 8,90 | 8,75 | 8,85 | 0,6 | 1,1 |
| 300 | AC 22 alap (F) | Jobb | 8,65 | 8,30 | 8,30 | 4,2 | 0,0 | |
| 370 | AC 22 alap (F) | Jobb | 8,90 | 8,92 | 8,95 | 0,6 | 0,3 | |
| 260 | AC 22 alap (F) | Bal | 8,34 | 8,34 | 8,10 | 3,0 | 3,0 | |
| 300 | AC 22 alap (F) | Bal | 7,58 | 7,19 | 7,70 | 1,6 | 6,6 | |
| 370 | AC 22 alap (F) | Bal | 7,55 | 7,55 | 7,50 | 0,7 | 0,7 | |
| 260 | AC 22 kötő (F) | Jobb | 5,94 | 6,69 | 6,40 | 7,3 | 4,5 | |
| 300 | AC 22 kötő (F) | Jobb | 6,06 | 5,73 | 6,10 | 0,7 | 6,1 | |
| 370 | AC 22 kötő (F) | Jobb | 5,82 | 5,42 | 5,60 | 3,9 | 3,2 | |
| 260 | AC 22 kötő (F) | Bal | 6,40 | 6,42 | 6,60 | 3,0 | 2,7 | |
| 300 | AC 22 kötő (F) | Bal | 6,76 | 6,68 | 6,80 | 0,6 | 1,8 | |
| 370 | AC 22 kötő (F) | Bal | 7,82 | 7,45 | 7,80 | 0,3 | 4,5 | |
| 3 | 260 | AC 22 alap (F) | Jobb | 8,37 | 8,87 | 8,85 | 5,4 | 0,2 |
| 300 | AC 22 alap (F) | Jobb | 8,83 | 7,75 | 8,30 | 6,4 | 6,6 | |
| 370 | AC 22 alap (F) | Jobb | 7,12 | 8,74 | 8,95 | 20,4 | 2,3 | |
| 260 | AC 22 alap (F) | Bal | 8,19 | 8,09 | 8,10 | 1,1 | 0,1 | |
| 300 | AC 22 alap (F) | Bal | 8,93 | 7,63 | 7,70 | 16,0 | 0,9 | |
| 370 | AC 22 alap (F) | Bal | 7,80 | 8,57 | 7,50 | 4,0 | 14,3 | |
| 260 | AC 22 kötő (F) | Jobb | 6,21 | 6,72 | 6,40 | 3,0 | 5,0 | |
| 300 | AC 22 kötő (F) | Jobb | 6,68 | 5,65 | 6,10 | 9,5 | 7,4 | |
| 370 | AC 22 kötő (F) | Jobb | 7,25 | 5,76 | 5,60 | 29,5 | 2,9 | |
| 260 | AC 22 kötő (F) | Bal | 6,48 | 7,97 | 6,60 | 1,8 | 20,8 | |
| 300 | AC 22 kötő (F) | Bal | 6,68 | 6,81 | 6,80 | 1,8 | 0,1 | |
| 370 | AC 22 kötő (F) | Bal | 8,39 | 7,17 | 7,80 | 7,6 | 8,1 | |
| 330 | AC 11 kopó (F) | Bal | 3,66 | 4,08 | 4,00 | 8,5 | 2,0 |
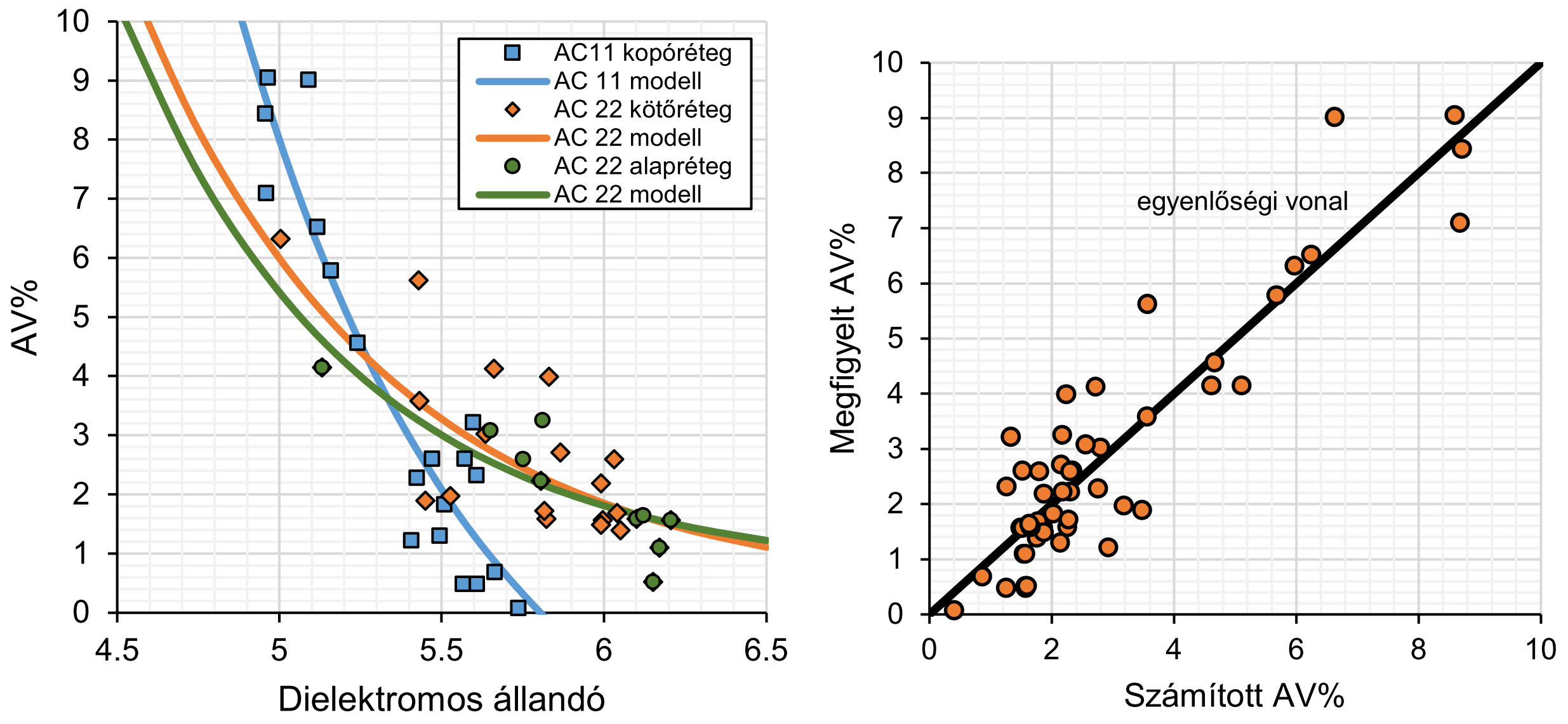 |
A vastagságmérések után rátérünk a földradarral meghatározott testsűrűség és szabadhézag-tartalom kiértékelésére. A helyszínen mért dielektromos állandó és az aszfaltkeverék szabadhézag-tartalma között a kapcsolatot a (7) összefüggéssel határoztuk meg. A helyszínen mért és a modellel számolt értékeket a 9. ábra mutatja be. Az AC 22 kötő- és alapréteg között nem volt tapasztalható nagy eltérés, mivel a két keverék igen hasonló volt egymáshoz. A modell paramétereit mind a három keveréktípusra a 3. táblázat tartalmazza. Előzetesen meghatároztuk, hogy a két változó, azaz a szabadhézag-tartalom és a dielektromos állandó kötötti összefüggést R2 ≥ 0,60 esetén tekintjük csak elfogadhatónak. Szerencsére ez a kritérium mind a három aszfaltrétegnél teljesült. A legmagasabb RMS hibát az AC 11 kopórétegnél találtuk és mivel az \( \epsilon \) hibatag is itt volt a legmagasabb, ezt a modellt végül nem tudtuk használni. Általánosságban kijelenthető, hogy a (7) modell jól tudja előre jelezni a szabadhézag-tartalmat a dielektromos állandóból, mivel a mért és a becsült értékek egy 45°-os egyenesre esnek és a pontok szóródása is kielégítő (9. ábra jobb oldala). Felhasználva mindegyik keverék laboratóriumban meghatározott \(G_{mm} \) értékét, a szabadhézagból a (6) képlettel testsűrűséget számoltunk.
| Keverék | α | β | RMSE | R2 | |
| AC 11 kopóréteg | 9174,405 | −1,325 | −4,1985 | 1,034 | 0,88 |
| AC 22 kötőréteg | 3642,681 | −1,292 | +0,2854 | 0,880 | 0,62 |
| AC 22 alapréteg | 5546,240 | −1,412 | +0,6506 | 0,559 | 0,71 |
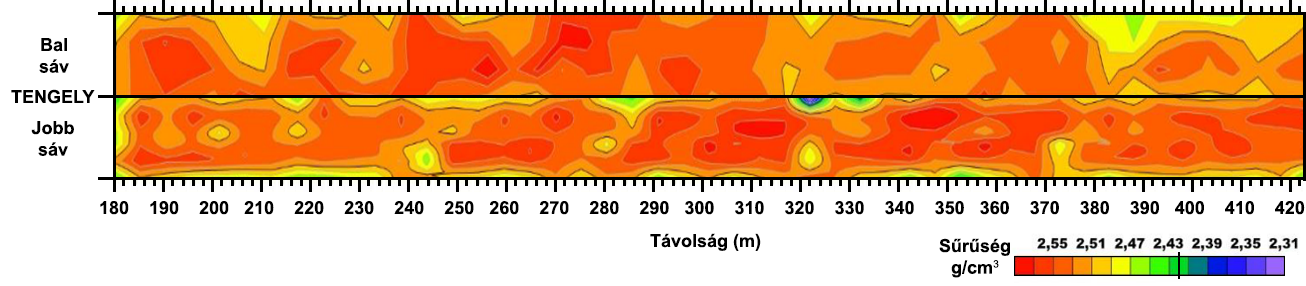
Az AC 22 aszfalt alapréteg sűrűségtérképét elemezve megállapítható, hogy a jobb sávban az aszfaltsűrűség a sávközépen a legmagasabb, míg a padka felé haladva az értékek fokozatosan csökkennek. Ezzel szemben a bal sávban az aszfaltsűrűség többé-kevésbé homogén a 0+370 szelvényig, ahonnan kezdve egy jelentősebb sűrűségcsökkenés megfigyelhető az úttengely környezetében. Az AC 22 aszfalt kötőréteg sűrűségtérképét elemezve megállapítható, hogy mind a jobb, mind pedig a bal sávban az aszfaltsűrűség a sávközépen a legmagasabb, míg az úttengely felé haladva az értékek fokozatosan csökkennek.
 |
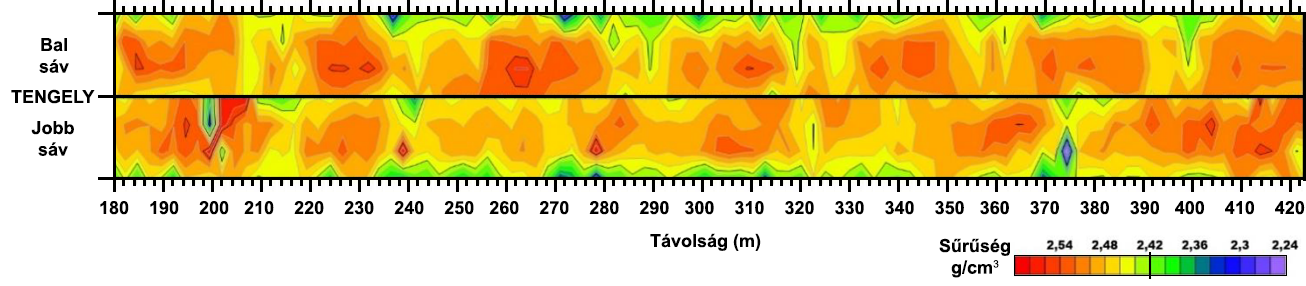 |
A bemutatott két sűrűségtérkép jól szemlélteti azt, hogy a beépített aszfaltanyagok testsűrűsége nem lesz egyenletes a teljes útfelületen, mivel az építési nehézségek rögtön megmutatkoznak minőségcsökkenés képében. Ebből következik, hogy az aszfaltsűrűség a sávközépen a legmagasabb, míg az úttengely felé haladva a sűrűségértékek fokozatosan csökkenek. Az aszfaltalap- és kötőréteg sűrűségtérképeit összehasonlítva pedig az is megállapítható, hogy az alaprétegen mért sűrűségértékek magasabbak, tehát az alapréteg jobban lett tömörítve, mint a kötőréteg.
Az AC jelű aszfaltkeverékből épített új kopóréteg előírt átlagos hézagtartalma legfeljebb 6% (a megfelelőségi határ 7%), az új kötő- és az új alapréteg előírt átlagos hézagtartalma legfeljebb 7% (a megfelelőségi határ 8%) lehet az e-ÚT 06.03.21/M1 szerint, ha a mintaszám ≥ 10 db. A Texas Department of Transportation (1995) [16] szerint, ha a szabadhézag-tartalom 8,5% és 9,9% közötti, akkor már jelentős értékcsökkenésről beszélünk; míg 9,9% feletti \(V_{A} \) -nál az útburkolatot el kell távolítani és újra kell építeni [17]. Ennek megfelelően kiszámítottuk minden egyes réteg esetén a \(V_{A} \) =6% ‒ 7% ‒ 8%szabadhézag-tartalomhoz tartozó testsűrűség és dielektromos állandó küszöbértékeket. A számítás eredményét a 4. táblázat foglalja össze. A 4. táblázatból jól látszik, hogy az alapréteg és a kötőréteg testsűrűség határértéke három tizedesjegyre kiszámítva is megegyezik, míg az ehhez a testsűrűséghez tartozó dielektromos állandó már mutat kismértékű eltérést. Ez azért lehet mert a sűrűség jóval kisebb tartományban változik, mint a hozzá tartozó dielektromos állandó. Ezért a testsűrűség helyett a dielektromos állandóra vagy a szabadhézagra célszerű határértéket megfogalmazni, amikor a földradar méréseket kiértékeljük.
| Keverék | VA 6% | VA 7% | VA 8% | |||
| Gmb | εAC | Gmb | εAC | Gmb | εAC | |
| AC 11 kopóréteg | 2,304 | 5,13 | 2,279 | 5,06 | 2,255 | 5,00 |
| AC 22 kötőréteg | 2,421 | 5,00 | 2,396 | 4,87 | 2,370 | 4,77 |
| AC 22 alapréteg | 2,421 | 4,92 | 2,396 | 4,80 | 2,370 | 4,69 |
 |
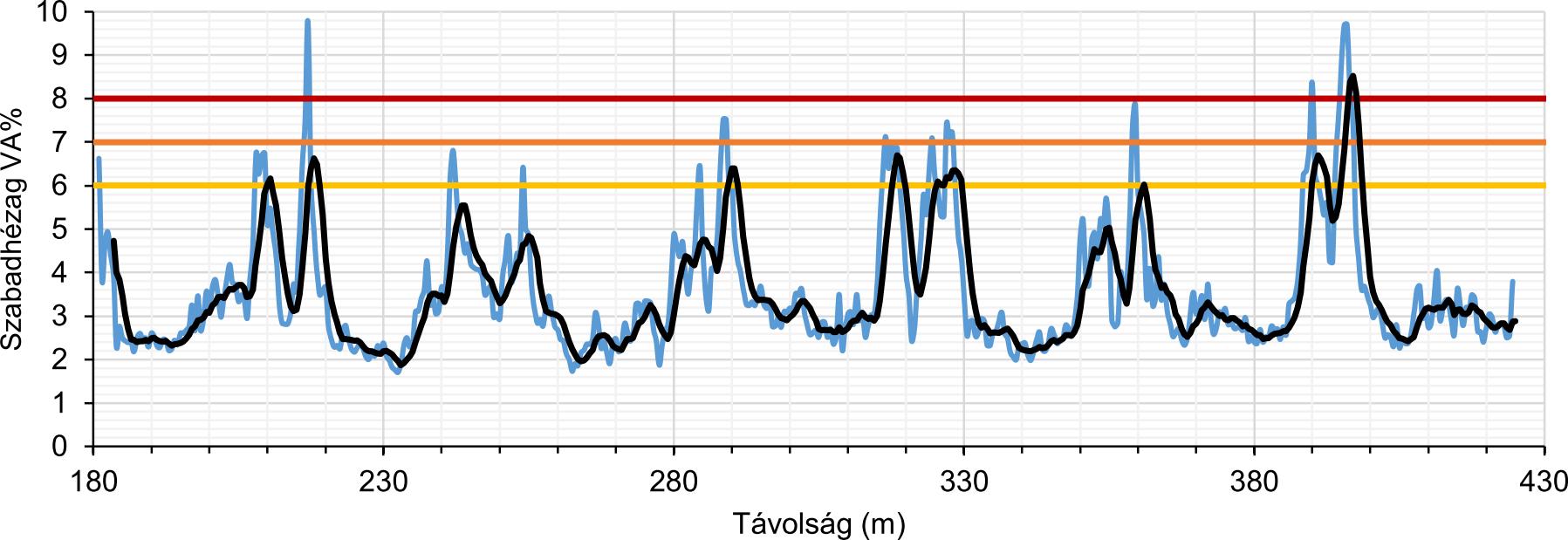 |
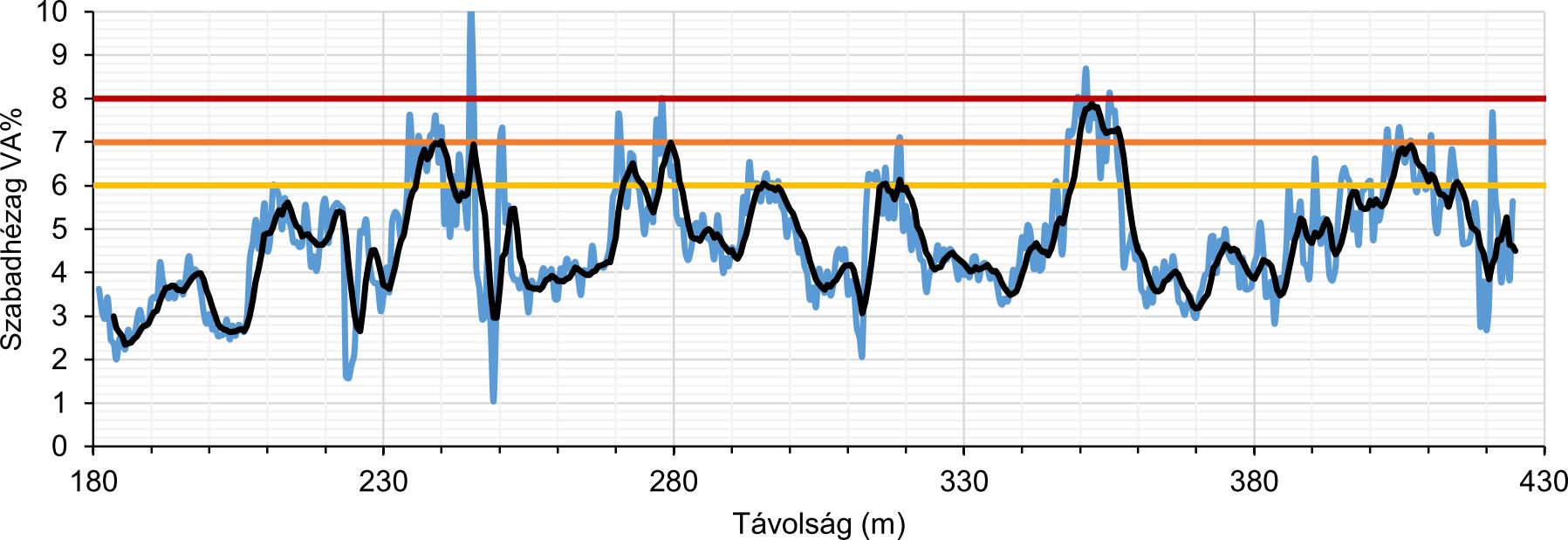
A könnyebb áttekinthetőség kedvérét bemutatjuk még az AC 22 kötőréteg baloldali sávszélének (a padkától 0,1 m-re) és sávközepének (a padkától 1,7 m-re) a szabadhézag profilját (lásd 12–13. ábra). Berajzolva az ábrákra a 6%–7%–8% hézagtartalomhoz tartozó küszöbértékeket egyből megkapjuk a nem megfelelő vagy bizonytalan minőségű szakaszok szelvényhatárait. Mivel kötőréteg esetén a megfelelőségi határ 8%, ezért a mérésekre illesztett fekete színű mozgóátlag görbe érintési vagy metszéspontját kell megkeresnünk a vízszintes vörös határvonallal. Viszont, ha figyelembe vesszük a modell bizonytalanságát (ami átlagosan 0,6-0,8%-ra tehető), akkor helyesebb, ha a narancssárga (előírt) és a vörös (megfelelőségi) határvonalak közötti tartományt tekintjük nem megfelelőnek. Ezt elfogadva megállapíthatjuk, hogy a burkolat szélén a 0+370 és 0+380 szelvények közötti 10 méter hosszú útszakasz tömörsége nem megfelelő, de a 0+235 és 0+250 szelvényhatárok közötti 15 m-es útszakaszt is érdemes még tovább vizsgálni. A sávközépnek viszont csak a 0+395 és 0+400 szelvények közötti útszakasza esik a nem elfogadható szabadhézag tartományba.
A vizsgált kísérletű útszakaszon mind a 12 db fúrt magminta szabadhézag-tartalma jellemzően 2-5% között változott, így gyengébb minőségű építési szakaszokat nem jeleztek előre. Ebből is látható, hogy a földradar technológia legnagyobb előnye az, hogy igen nagy az adatsűrűség, valamint gyorsan és relatív pontosan képes dielektromos vagy testsűrűség vagy szabadhézag térképeket és profilokat előállítani. Ezek a térképek pedig ideálisak arra, hogy a gyengébben vagy éppen a jobban tömörített útszakaszokat lehatároljuk és azok minőségét fúrt mintával igazoljuk.
Összefoglalás
A cikkben bemutatott mérések és azok feldolgozása alapján javasoljuk, hogy újépítésű pályaszerkezeti rétegek vastagságmérésénél minden réteg közé be kell építeni alumínium fólia antipólusokat, mivel ezek nagymértékben megnövelik a földradar adatok kiértékelésének pontosságát. Hasonlóan az örvényáramos vastagságmérés technikához, ahol a réteg terítése előtt a fogadófelületre szintén egy antipólust helyeznek le, ami sok esetben szintén egy egyszerű alumíniumlap [18].
A vizsgált délalföldi lakóutca 220–240 m hosszú kísérleti útszakaszának tapasztalatai azt mutatják, hogy célszerű minden réteg terítése és betömörítése után az aktuális réteg felszínén elvégezni a földradar méréseket. A mért adatokból pedig csak az éppen vizsgált réteg vastagságát felhasználni a minőségellenőrzéshez. Ez az eljárás ugyan több mérést igényel, de sokkal pontosabb lehet, mint az egyszeri, a kész pályaszerkezet felszínén történő vastagságmérés. A többletmérés másrészt lehetővé teszi, hogy minden réteg testsűrűség vagy szabadhézag tartalmát is megállapítsuk.
Az aszfaltkeverékek dielektromos állandója és azok szabadhézag-tartalma között erős kapcsolatot találtunk, hasonlóan a nemzetközi szakirodalomhoz. Szisztematikus adatgyűjtéssel olyan empirikus modell fejleszthető, amivel a \( V_{A} \) értékeket ±1% pontosan meg lehet becsülni. Erre a célra legjobban a fúrások helyén megmért dieletromos állandók és a fúrt minták laboratóriumban meghatározott hézagjellemzői használhatóak fel. Valójában erre nincs is mindig szükség, hiszen határértéket közvetlenül a dielektromos állandóra is megfogalmazhatunk. Újra felhívjuk a figyelmet arra a tényre, hogy a különböző utakról gyűjtött GPR adatok már bizonyították, hogy a dielektromos állandó értékének csökkenése mindig sűrűségproblémákat jelez előre! Ezért az első hengerjárat után mért dielektromos állandó térképek már jó viszonyítási alapot adnak a későbbi kiértékelésekhez.
Összefoglalva kijelenthetjük, hogy a roncsolásmentes útdiagnosztikai módszerek közül a földradarok és az intelligens úthengerek (Intelligent Compaction, IC) képesek egyedül biztosítani az aszfaltkeverék folyamatos kvantitatív tömörségének meghatározását. Viszont továbbra is csak a földradar módszer alkalmas a tömörség mellett az útpályaszerkezet rétegvastagságnak a meghatározására is, így az építési minőség ellenőrzésére jó szívvel ajánlható.
Irodalomjegyzék
[1]: Goel, A. & Das, A. 2008: Nondestructive Testing of Asphalt Pavements for Structural Condition Evaluation: A State of the Art. Nondestructive Testing and Evaluation 23 (2): 121–40. https://doi.org/10/fdtqhf.
[2]: Tóth, C. & Primusz, P. 2021: Modern roncsolásmentes útdiagnosztikai eszközök. Az Aszfalt 28 (1): 33–47.
[3]: Pattantyús-Á., M., Neducza, B., Prónay, Z. & Törös, E. 1994: A földradar módszerfejlesztés másfél éves tapasztalatai az ELGI-ben. Magyar geofizika 35 (1): 32–41.
[4]: Katona, O., Sipos, G., Fiala, K., Rakonczai, J. & Mezősi, G. 2013: A georadar működése és felhasználási területei. Hidrológiai közlöny 93. évf. (4. sz.): 55–60.
[5]: Kóti, Á. 2014: Közforgalmú utak úthibáinak roncsolásmentes vizsgálata földradar segítségével. Diplomamunka, Miskolc: Miskolci Egyetem.
[6]: Maser, K. R. & Scullion, T. 1992: Automated Pavement Subsurface Profiling Using Radar: Case Studies of Four Experimental Field Sites. Transportation Research Record 1344: 148–54.
[7]: Krysiński, L. & Sudyka, J. 2013: GPR Abilities in Investigation of the Pavement Transversal Cracks. Journal of Applied Geophysics 97 (október): 27–36. https://doi.org/10.1016/j.jappgeo.2013.03.010.
[8]: Diamanti, N. & Redman, D. 2012: Field Observations and Numerical Models of GPR Response from Vertical Pavement Cracks. Journal of Applied Geophysics 81 (június): 106–16. https://doi.org/10.1016/j.jappgeo.2011.09.006.
[9]: Sudyka, J. & Krysi, L. 2011: Radar Technique Application in Structural Analysis and Identification of Interlayer Bonding. International Journal of Pavement Research & Technology 4 (3): 10.
[10]: Lambot, S., Weihermüller, L., Huisman, J. A., Vereecken, H., Vanclooster, M. & Slob, E. C. 2006: Analysis of Air-Launched Ground-Penetrating Radar Techniques to Measure the Soil Surface Water Content. Water Resources Research 42 (11). https://doi.org/10/b7rkw2.
[11]: Petőcz, M., Schváb, J. & Szarka, I. 1999: Útpályaszerkezeti rétegek roncsolásmentes vastagságmérése. Közúti és mélyépítési szemle 49 (6): 219–25.
[12]: Runa, B. & Balogh, P. 2021: Georadar szerepe a roncsolásmentes útpályadiagnosztikában. Az Aszfalt XXVIII. (2): 49–56.
[13]: Saarenketo, T. 1997: Using Ground-Penetrating Radar and Dielectric Probe Measurements in Pavement Density Quality Control. Transportation Research Record: Journal of the Transportation Research Board 1575 (1): 34–41. https://doi.org/10/d28cch.
[14]: Saarenketo, T. & Scullion, T. 2000: Road Evaluation with Ground Penetrating Radar. Journal of Applied Geophysics 43 (2–4): 119–38. https://doi.org/10.1016/S0926-9851(99)00052-X.
[15]: Hoegh, K., Roberts, R., Dai, S. & Zegeye Teshale, E. 2019: Toward Core-Free Pavement Compaction Evaluation: An Innovative Method Relating Asphalt Permittivity to Density. Geosciences 9 (7): 280. https://doi.org/10/ghgqbc.
[16]: TxDOT 2004: Standard Specifications for Construction and Maintenance of Highways, Streets, and Bridges. Texas Department of Transportation.
[17]: Chen, D.-H., Hong, F., Zhou, W. & Ying, P. 2014: Estimating the Hotmix Asphalt Air Voids from Ground Penetrating Radar. NDT & E International 68 (december): 120–27. https://doi.org/10/f6p8h5.
[18]: Pethő, L. & Tóth, C. 2010: Beépített aszfaltrétegek vastagságának roncsolásmentes meghatározása. Közlekedésépítési szemle 60 (8): 15–19.
Erre a szövegre így hivatkozhat:
Primusz Péter, Runa Boglárka, Balogh Olivér, Tóth Csaba: Új építésű aszfaltrétegek vastagságának és tömörségének meghatározása földradarral, 2022, DOI: 10.36246/UL.2022.1.04
