Bevezetés
A BRCC (Belgian Road Research Center) Belga Útügyi Kutató Központban az 1970-es években úttörő jelentőségű, átfogó kutatásokat végeztek a melegaszfalt keverékek triaxiális vizsgálatai (triaxial cyclic compression test, TCCT) terén. A kutatás fő célja egy olyan modell kifejlesztése volt, amely a melegaszfalt keverékek plasztikus deformációs viselkedését képes leírni. Ennek megfelelően a kutatás során számos tényező hatását tanulmányozták a különböző peremfeltételek mellett szisztematikusan megtervezett vizsgálatsorozatok során. A Francken által publikált modell (Francken, 1977) a mai napig használatos a triaxiális terhelésből származó függőleges irányú plasztikus alakváltozás becslésére, a kutatás pedig az aszfaltkeverékek triaxiális vizsgálataira vonatkozó EN 12697-25:2005 szabvány kidolgozása során annak egyik legnagyobb forrásává vált. Jaeger (Jaeger, 1980) különböző melegaszfalt keverékeket vizsgált magas hőmérsékleten, ismételt szinuszos terhelés alatt, állandó palástnyomás mellett. Megmutatta, hogy a plasztikus alakváltozást a legnagyobb mértékben a függőleges terhelés befolyásolja, ezt követi a hőmérséklet és a terhelés frekvenciája. A technológia fejlődése később lehetővé tette az adatok digitalizálását, tárolását, feldolgozását, ezáltal a vizsgálati eredmények részletesebb kiértékelését és elemzését, melyet Weiland kutatásai során ki is használt (Weiland, 1986). A feszültségek és alakváltozások amplitúdóinak mérése és megjeleníthetősége lehetővé tette a közöttük lévő fázisszög első megfigyeléseit. A Weiland által bemutatott vizsgálati eredmények kimutatták, hogy a tengelyirányú terhelés és alakváltozás, valamint a tengelyirányú terhelés és radiális alakváltozás fázisszögei eltérnek. Azt is kimutatta, hogy a fázisszög szempontjából meghatározó a hőmérséklet szerepe. Az 1990-es években von der Decken egy kiterjedt kutatásban különböző melegaszfalt keverékeket különböző hőmérsékleteken vizsgált TCCT-vel (von der Decken 1997). Érdekes módon azt találta, hogy létezik egy állandó fázisszög a tengelyirányú terhelés és radiális alakváltozás között, mely független a keverék összetételétől és a hőmérséklettől. A fázisszög értékét 36°-ban állapította meg.
A közelmúltban Kappl végzett átfogó kutatást a TCCT vizsgálatokkal kapcsolatban (Kappl, 2007). Ennek során egy kiterjedt program keretében számos, különféle adalék- és kötőanyag összetételű aszfaltkeveréket vizsgált TCCT-vel az EN 12697-25:2005 szerint. Kapcsolatot keresett a TCCT eredmények és a különféle kötőanyag-típusok, illetve olyan egyszerű vizsgálati eredmények között, mint a Marshall vizsgálatok. A kutatás fő eredményeként jó korrelációt tapasztaltak a kötőanyag gyűrűs-golyós lágyuláspontja és az 50°C hőmérsékleten mért, 25.000 ciklus után összegzett tengelyirányú alakváltozás között. Hasonlóképpen a hézagtartalom összekapcsolható a standard TCCT vizsgálat során mért kúszássebesség jellemzőkkel.
A TCCT módszert 2004-ben integrálták az európai harmonizált normarendszerbe az EN 12697-25:2005 szabvány formájában mint a melegaszfalt keverékek magas hőmérsékleten történő maradó alakváltozással szembeni ellenálló képesség vizsgálati módszerét. A szabványos vizsgálati módszer olyan ciklikus tengelyirányú terhelésből áll, mely egy gumiabroncs áthaladását szimulálja, valamint egy állandó oldalnyomásból, mely a pályaszerkezetben lévő oldalsó megtámasztás hatását képviseli. A tengelyirányú plasztikus deformációt a ciklusszám függvényében elemzi, melynek eredménye a kúszási görbe.
A CCT vizsgálat viszont a melegaszfalt keverékek anyagi jellemzőinek vizsgálatára (merevség, fázisszög) is alkalmas, ha azt az anyag lineáris viszkoelasztikus tartományában alkalmazzuk. Ilyenkor a vizsgálatot a frekvencia és hőmérséklet söpréssel kell elvégezni (Hofko, 2011). A keresett anyagparamétereket az alkalmazott terhelés (akció) és a bekövetkező anyagreakció (pl. alakváltozás) alapján kapjuk meg (Di Benedetto et. al, 2001). A különböző, feszültséget és alakváltozást is tartalmazó vizsgálatoktól eltérően (például EN 12697-26 szerinti közvetlen húzásvizsgálat), ahol – mivel feszültségátadás történik – a próbatest és a terhelő lemezek között erős kapcsolat szükséges, a CCT esetén két lehetőség áll rendelkezésre. Egyik (a) a próbatestek terhelő lemezekhez való ragasztásával a történhet, amely erős kapcsolatot eredményez. Ez megakadályozza a keresztirányú feszültségek kialakulását a próbatest határoló síkjain és azok közelében. A másik (b) módszer, mellyel még homogénebb feszültségeloszlás érhető el, amikor a próbatest és a terhelő lemezek között nincsen erős kapcsolat. Ekkor súrlódáscsökkentő szerek alkalmazásával (pl. szilikon zsír) segítik elő a feszültség homogén eloszlását a próbatest határoló síkjain. Jelen kutatásban azt vizsgáljuk, a két módszer közötti eltérés, azaz a próbatest és a terhelő lemezek közötti kapcsolat hatással van-e a melegaszfalt keverékek viszkoelasztikus tartományában mért anyagjellemzőkre. A vizsgálati eredmények regresszió-analízisére használt, a rezgés első harmonikusát is tartalmazó egyenlet felhasználható a torzult szinuszos jelek elemzésére, ezáltal a berendezések és érzékelők fizikai korlátainak felfedésére.
Anyagok és a vizsgálati terv
Anyagok és próbatestek
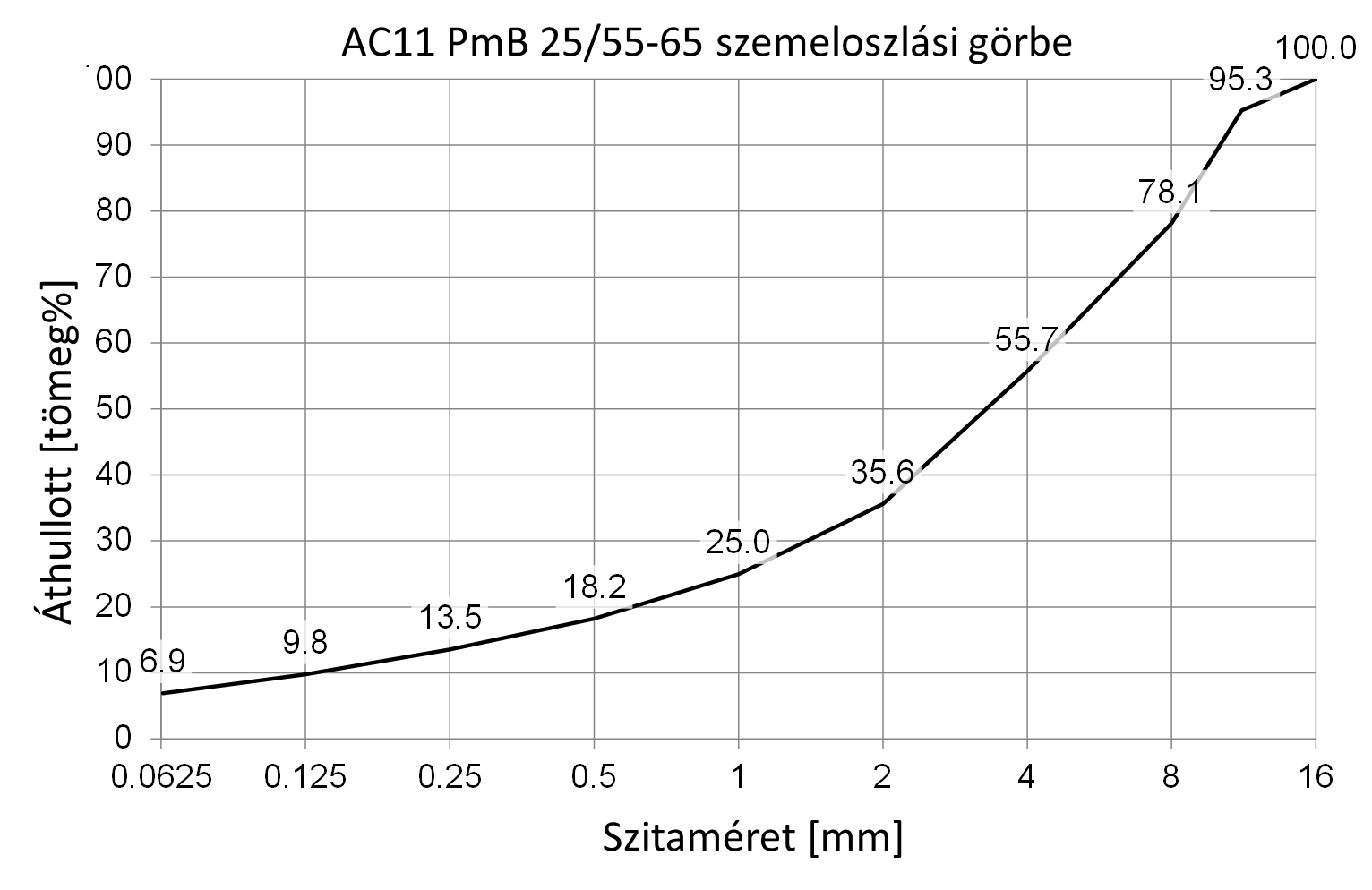
A bemutatott kutatáshoz 11 mm névleges szemcsenagyságú aszfaltbeton keveréket (AC11) használtunk, mely zúzott kőanyagból, mészkőliszt töltőanyagból, valamint SBS modifikált, PmB 25/55-65 kötőanyagból állt. A kötőanyag fő jellemzőit az 1. táblázat tartalmazza. Az optimális kötőanyag-tartalom 5,3 m% volt. Az 1. ábra a keverék szemeloszlását mutatja.
| Paraméter | Érték |
| Penetráció 25°C-on | 46,0 1/10 mm |
| Gyűrűs-golyós lágyuláspont | 73,0 °C |
| SHRP szerinti teljesítményfokozat | >82-16 |
 |
Az aszfaltkeveréket irányváltós kényszerkeverővel készítettük el. A forró bitumen hozzáadását az előmelegített adalékanyagok és töltőanyag 1 perces keverése előzte meg. A kötőanyag hozzáadása után további három perces keverés következett. Ezután hengeres szegmenstömörítő berendezéssel 500 x 260 mm alapterületű, 130 mm magas lapok készültek. Az egyrétegű tömörítés során a próbatestben fellépő sűrűség egyenlőtlen eloszlásának elkerülése érdekében a lapok két rétegben készültek (Hoeflinger, 2006). Szintén Hoeflinger szerint, a próbatestekben lévő két réteg jelenléte nem befolyásolja az eredményeket az egy rétegben gyártott, homogén lapokból vágott próbatestekhez képest.
Minden lapból négy darab 100 mm átmérőjű hengeres próbatest került kifúrásra. A fúrt próbatesteket ezután 200 mm magasságúra fűrészelték. A 2. ábra a szegmens lapokat és a belőlük fúrt próbatestek elhelyezkedését mutatja.
 |
Vizsgálati összeállítás és kísérleti terv
A próbatest és a terhelő lemezek közötti kapcsolat, valamint a mért viszkoelasztikus anyagjellemzőkre gyakorolt hatásának két különböző vizsgálati elrendezést alkalmaztunk. A 3. ábra bal oldala a standard CCT vizsgálatot mutatja, melyben nincs teljes kapcsolat a próbatest és a terhelő lemezek között. Itt a próbatest határoló lapjaira felvitt szilikon zsír csökkenti a súrlódást, emiatt a próbatest végeinél egyenletes eloszlású, keresztirányú alakváltozás jön létre. Az ábra jobb oldalán a terhelő lemezekhez kétkomponensű ragasztóval rögzített próbatest látható. Ebben az esetben a próbatest felületén nem jön létre keresztirányú alakváltozás.
 |
Mindkét elrendezés alkalmazásával négy-négy próbatestet vizsgáltunk. A próbatestek adatait a 2. táblázat tartalmazza. A kutatás előkészítése során előzetes CCT vizsgálatok történtek több hőmérsékleten (10°C, 30°C, 50°C) és több feszültségszinten a próbatestek lineáris viszkoelasztikus tartományának azonosítása érdekében. Airey szerint melegaszfaltok esetében 10-4, vagy annál kisebb megnyúlást előidézve az anyag biztosan a lineáris viszkoelasztikus tartományban marad (Airey et. al, 2003). Az előzetes vizsgálatok eredményei alapján látható, hogy a 30°C hőmérsékleten, 0,25 N/mm2 átlagos nagyságú és 0,15 N/mm2 amplitúdójú tengelyirányú feszültség esetén a próbatestekben legfeljebb 10-4 alakváltozás keletkezik, így a próbatest a lineáris viszkoelasztikus tartományban marad. A frekvencia söpréssel a 0,1 – 10 Hz frekvenciatartományban végzett vizsgálatok ciklusszámait és eredményeit a 3. táblázat tartalmazza.
| Próbatest jele | Hézagtartalom [% (v/v)] | Ragasztott / Nem ragasztott |
| T404C | 6,4 | Nem ragasztott |
| T406E | 5,5 | |
| T406G | 5,0 | |
| T406H | 7,0 | |
| T404A | 3,8 | Ragasztott |
| T405C | 3,5 | |
| T406A | 5,2 | |
| T406B | 3,5 |
| Frekvencia | 0,1 | 0,5 | 1,0 | 3,0 | 5,0 | 10,0 |
| Terhelési ciklusszám | 20 | 50 | 100 | 100 | 200 | 200 |
A függőleges alakváltozást a felső terhelő lemezen elhelyezett két LVDT elmozdulásmérő rögzítette. Az adatfeldolgozáshoz a két adó jelének átlagát használtuk. A radiális összenyomódást a próbatestek felszínén elhelyezett nyúlásmérő bélyegek mérték. A 150 mm aktív hosszúságú bélyegeket a próbatest magasságának felében, körmentén helyeztük el.
Annak érdekében, hogy a CCT vizsgálatok eredményei egy elfogadott, szabványos merevségvizsgálat
(EN 12697-26:2004) eredményeivel összehasonlíthatóak legyenek, az ugyanazon keverékből gyártott négy próbatestet négypontos hajlítóvizsgálatnak vetettük alá. A vizsgálatok 30°C-on, 0,1-10 Hz közötti frekvenciatartományban történtek. A vizsgálatok során 35 µm/m megnyúlást állítottunk be. A vizsgálati próbatestek jellemzőit a 4. táblázat tartalmazza.
| Próbatest jele | Hézagtartalom [% (v/v)] |
| E454A | 4,3 |
| E454B | 4,6 |
| E454D | 3,9 |
| E454F | 4,0 |
Az adatok kiértékelése
Az erő- és elmozdulásmérők jeleit regresszió-analízissel vizsgáltuk az alábbi függvények szerint (1) (2):
\[f_{(t)}=a_{1}+a_{2}*sin(2{\pi}*f*t+a_{3})+a_{4}*t\]
\[f_{(t)}=a_{1}+a_{2}*sin(2{\pi}*f*t+a_{3})+a_{4}*t+a_{5}*sin(4{\pi}*{f}*{t}+a_{6})\]
| Ahol, | |
| a1 | az alaprezgés eltolása, |
| a2 | az alaprezgés amplitúdója, |
| a3 | az alaprezgés fázisszöge, |
| a4 | a lineáris tag meredeksége, |
| a5 | az első harmonikus amplitúdója, |
| a6 | az első harmonikus fázisszöge, |
| f | a rezgés frekvenciája, |
| t | az idő, |
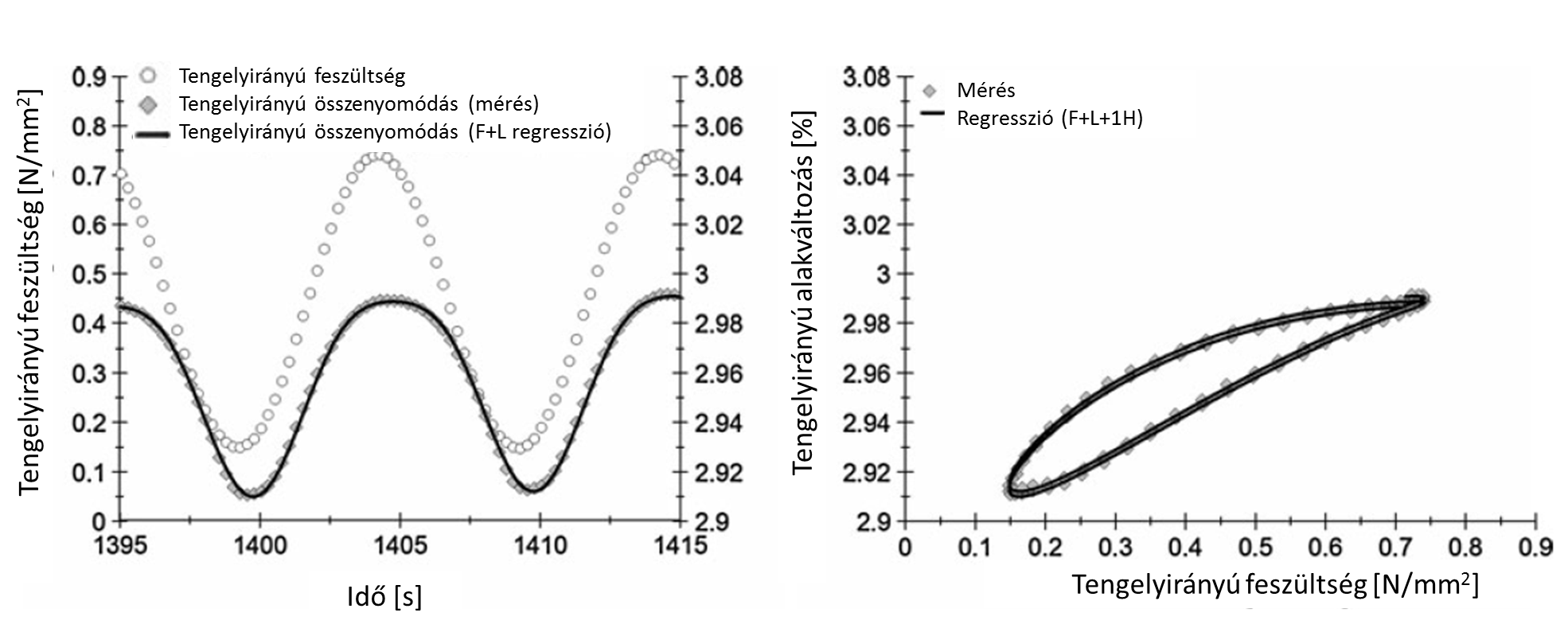
Az (1) egyenletet a továbbiakban F+L-el jelöljük, tekintve két tagját, egy alaprezgés (F) és egy lineáris szakasz (L) egyenletét. A (2) egyenletet F+L+1H-val jelölik, mivel az előzőek mellett a rezgés első harmonikusát (1H) is tartalmazza. Az elemzés megkönnyítése érdekében az adatokból 3 terhelési ciklusból álló adatcsoportokat képeztek, melyek megfelelő alapként szolgálnak a regresszió analízishez. Ezután elvégezték a regresszió analízist. Az összetettebb, F+L+1H egyenlet alkalmazásával, az első harmonikus paramétereinek köszönhetően a szinuszos jel torzultsága matematikailag vizsgálható. A CCT vizsgálat során mért tengelyirányú alakváltozás Kappl [6] szerint nem írható le az egyszerű F+L (1) regressziós egyenlettel. A 4. ábra a CCT eredmények F+L egyenlettel való közelítését ábrázolja. A baloldal a tengelyirányú feszültség (σax) és alakváltozás (εax) alakulását mutatja két periódus hosszon az idő függvényében, illetve az εax függvény regressziós közelítését. Részletesebben vizsgálva látható, hogy az egyszerű szinuszos és lineáris részből álló egyenlet nem írja le megfelelően a CCT vizsgálat során mérhető deformációt.
 |
A közelítés függvényének a terhelés maximumánál mért alakváltozás görbéje szélesebb és laposabb, míg a legkisebb terhelésnél az alakváltozás keskenyebb és magasabb a csúcspontja. Az ábra jobb oldala ugyanannak a mérésnek a feszültség-alakváltozás ábráját mutatja. Az ábrán jobban látható, hogy a mérési adatok jobban eltérnek az F+L közelítéstől, vagyis hogy az összefüggés nem képes kielégítő pontossággal leírni a mért adatokat. Az adatsorok, különösen a terhelési és tehermentesítési fázisban, torzulást mutatnak a szinuszos közelítéshez viszonyítva. Erre az esetre Kappl bevezetett egy összetettebb közelítő függvényt a CCT vizsgálatok esetére, az F+L+1H alakú regressziós függvényt. Az eredetihez egy második szinuszos tagot adott hozzá, mely a rezgés első harmonikusát képviseli, és az alaprezgés frekvenciájának kétszeresére vonatkozik. Az 5. ábra a 4. ábra adataira illesztett F+L+1H alakú közelítést mutatja. A függvények összevetése alapján megállapítható, hogy az összetett függvénnyel a mért adatok jobban közelíthetőek, mint az egyszerű szinuszos egyenlettel. Ez egyaránt igaz a szélsőértékekre és a terhelési illetve tehermentesítési szakaszokra. Az F+L+1H megközelítés a torzult szinuszos jelekre is alkalmazható.
 |
Az összetett közelítő függvényt torzult szinuszhullámok esetén a torzulás mértékének és alakjának leírására használták (Kappl, 2007). A regressziós függvény alakját, szélsőértékeit és meredekségeit az első harmonikus és az alaprezgés aránya, valamint az első harmonikus és az alaprezgés közötti eltolási tényező is befolyásolja. Az amplitúdó arány (AR) a 3. egyenlet szerint:
\[AR=\frac{a_{5}}{a_{2}}\]
| Ahol, | |
| \(AR\) | az első harmonikus és az alaprezgés aránya [-] |
valamint a két szinuszos tag közötti shift-faktor:
\[\gamma=a_{6}-a_{3}\]
| Ahol, | |
| \(\gamma\) | az első harmonikus és az alaprezgés közötti shift faktor [°] |
Az első harmonikus hatása az alábbi elméleti példában adott paraméterek alapján illusztrálható. Az eltolás (a1), az alaprezgés fázisszöge (a3) és a lineáris tag (a4) értéke legyen zérus. Az alaprezgés amplitúdója (a2) legyen 1, a5 pedig egyenlő az AR amplitúdó aránnyal a 3. egyenlet szerint, ami 0,2. Az első harmonikus fázisszöge a (a6) -180° – 180° közötti tartományban mozog a paraméter hatásának szemléltetése érdekében. A vizsgálati eredmények javarészt ebben a tartományban mozognak. Mivel a3 zérus, a6 egyenlő a két szinuszos tag közötti γ shift-faktorral, a 4. egyenlet szerint. Az f frekvencia 0,1 Hz. A paramétereket az 5. táblázat foglalja össze.
| Paraméterek | Értékek | Részletek |
| a1 | 0 | Eltolás |
| a2 | 1 | Az alaprezgés |
| a3 | 0 | Az alaprezgés fázisszöge |
| a4 | 0 | A lineáris tag meredeksége |
| a5 = AR | 0,2 | Az első harmonikus amplitúdója |
| a6 = γ | −180° – 180° | Az első harmonikus fázisszöge |
| f | 0,1 Hz | Frekvencia |
 |
A 6. ábra kilenc esetet mutat, melyekben a γ shift-faktor az alaprezgés és az első harmonikus között szisztematikusan változik. A bal felső ábrán γ értéke 180°, mely ábránként 45°-kal nő, míg a jobb alsó ábrán végül a +180°. A közelítést az egyszerű szinuszos közelítéshez viszonyítva az alábbi megállapítások tehetőek.
A -180°-os shift faktor értéknél az első harmonikus hatása domináns a terhelési és tehermentesítési fázisban, és a szélsőérték alakja nem változik. A -180° és -90° közötti tartományban az első harmonikus hatása a másik szélsőérték felé tolódik el. A -90° értéknél a szélsőérték környéke egyértelműen deformálódik. A függvény alakját tekintve elmondható, hogy az első harmonikus tag hatása a szinuszgörbe deformációjára folyamatos, 90°-onkénti váltásokkal.
Világos tehát, hogy a fejlettebb összefüggés felhasználható adott szinusz görbe alakjának gyors vizsgálatára az AR és γ paraméterek felhasználásával. Az AR a torzulás mértékét (mennyiségét) mutatja, míg a γ shift faktor a torzulás módját (minőségét) jellemzi.
Az eredmények értékelése
A próbatest és a terhelő lemezek közötti kapcsolat viszkoelasztikus anyagjellemzőkre gyakorolt hatásának vizsgálatára méréssorozatot végeztünk a két vizsgálati elrendezés alkalmazásával, melyeket az alábbiakban összehasonlítunk. A mérési adatokra vonatkozóan regresszió analízist végeztünk F+L és F+L+1H alakú függvényekkel. A továbbiakban bemutatott diagramokon a folytonos vonal a „nem-ragasztott”, a szaggatott vonal a „ragasztott” elrendezés eredményeit mutatja, míg a vastag vonal a kettő átlagát. Az átlagértékek a két elrendezésben vizsgált 4-4 próbatest egyes frekvencián mért adataiból származnak. Az átlagértékkel párhuzamos vékony vonalak a 95%-os konfidencia intervallumhoz tartozó értékeket jelölik.
Az elemzés az erőmérők jelének vizsgálatával kezdődik. Mivel a vizsgálatokat erővezérelt módban végeztük, a jel elemzése a berendezés vezérlésének minőségéről ad információt, vagyis arról, hogy a műszer a szinuszos terhelést milyen pontosan képes létrehozni.
A következő lépés az elmozdulásmérők jelének vizsgálata. Érdekes látni, hogy az anyag reakciójának függvénye mennyire tükrözi a szinuszos terhelést az összenyomódási fázisban, illetve hogy van-e különbség a ragasztott és a nem ragasztott elrendezés közötti esetekben. A vizsgálat lezárásaként az adatokból számolt paramétereket (merevség és fázisszög) elemezzük mindkét elrendezés esetén a lineáris viszkoelasztikus tartományban. Az így kapott CCT eredményeket összehasonlítjuk a négypontos hajlításvizsgálattal kapott merevség értékekkel.
Az erőmérők jelének vizsgálata
Az alábbiakban az erőmérők ragasztott és nem-ragasztott vizsgálati elrendezés során rögzített jelének részletes elemzését mutatjuk be. A 7. ábra bal oldala az erőmérők jelének F+L alakú egyenlettel való közelítésének korrelációs együtthatóját mutatja a frekvencia függvényében, a két elrendezés esetében. Egyértelműen látható, hogy az illeszkedés a két elrendezés esetében megegyezik és a regresszió korrelációs együtthatója igen magas, 0,999 fölötti. Ez a magas korreláció azt mutatja, hogy a berendezés megbízhatóan működik a vizsgált tartományban egészen 10 Hz-ig, és a két elrendezés között nincs különbség.
A 7. ábra jobb oldala ugyanezt mutatja az F+L+1H alakú közelítés esetében. Hasonlóképpen a bal oldali ábrához, látható, hogy a két elrendezés között nincs különbség, valamint hogy a közelítés igen erős regressziós együtthatóval jellemezhető.
 |
Az, hogy az erő szinuszos függvényének alakja változik-e a frekvencia függvényében vagy a kétféle vizsgálati elrendezés között eltérő-e, az első harmonikus és az alaprezgés közötti AR amplitúdó arány és a γ shift faktor felhasználásával vizsgálható. E kettő több információt nyújt a korrelációs együtthatónál, hiszen együtt az eltérés minőségét és mennyiségét is leírják.
Az eredményeket a 8. ábra mutatja. Az ábra bal oldalán lévő amplitúdó arány diagramját tekintve látható, hogy lényegében nincs torzulás, hiszen AR értéke az alacsonyabb frekvenciák esetén is 1‰ alatt van. Habár a frekvencia növekedésével AR értéke nő, értéke mindvégig alacsony marad, még 10 Hz frekvencia esetén is csak 5‰ körüli, azaz a berendezés szinte torzulásmentes szinuszos terhelést ad le. Az AR frekvenciával növekvő tendenciája azonban azt jelzi, hogy a berendezés magas frekvenciákon nehezebben irányítja a terhelő egységet. A 95% konfidencia intervallumon számított AR érték alapján megállapítható, hogy a két elrendezés között nincs jelentős különbség, habár a nem-ragasztott beállítás esetében AR átlagértéke mintegy 20% magasabb, mint ragasztott elrendezés esetén.
A jobb oldali diagram a shift faktor értékeit mutatja. Hasonlóképpen az előzőekhez a két elrendezés a γ értékét tekintve sem tér el egymástól. Az eltérés alacsony frekvenciák esetén magas, de az alacsony AR arány miatt ez nem befolyásolja az erő becslését. A 10 Hz-en mért fázisszög -100° körüli, de az AR arány kis értéke miatt ez sem befolyásolja számottevően az erő szinuszos leadását.
 |
A bemutatottak alapján kijelenthető, hogy a terhelő rezgés alakját tekintve a berendezés megfelelő szinuszos jelet ad le. Az eredmények alapján szintén belátható, hogy a próbatest ragasztott, vagy nem-ragasztott volta nem befolyásolja számottevően az erő szinuszos alakját.
Az elmozdulásmérők jelének vizsgálata
A 9. ábra a tengelyirányú elmozdulásmérők jelét mutatja a két elrendezés esetén. Az ábra bal oldala az alap F+L függvénnyel való közelítés korrelációs együtthatóját mutatja. Látható, hogy mindkét elrendezés igen jól (R2>0,995) közelít a teljes vizsgált frekvencia tartományban. Az eltérés mindkét esetben hasonló.
Az adatok azt mutatják, hogy az egyszerű szinuszfüggvénnyel jobban közelíthető a deformáció magasabb frekvenciák esetén, 3 Hz-től kezdve a korrelációs tényező értéke 0,998 körüli vagy a fölötti. Alacsonyabb frekvenciák esetén, amikor az anyag viszkózus viselkedése még domináns, az egyszerű függvény gyengébben, de még elfogadható szinten írja le annak viselkedését.
A 9. ábra jobb oldala az F+L+1H függvénnyel való közelítés esetén kapott korrelációs együttható mutatja a két vizsgálati elrendezés esetén. Az egyszerűbb függvényhez képest a regresszió mindkét esetben számottevően erősebb. A nem-ragasztott vizsgálatok esetén az R2 0,999 fölötti a teljes vizsgált frekvenciatartományban, alacsony szórással. Az illeszkedések közötti különbség különösen alacsony frekvenciák esetében látható, amikor a viszkózus anyagviselkedés dominánsabb.
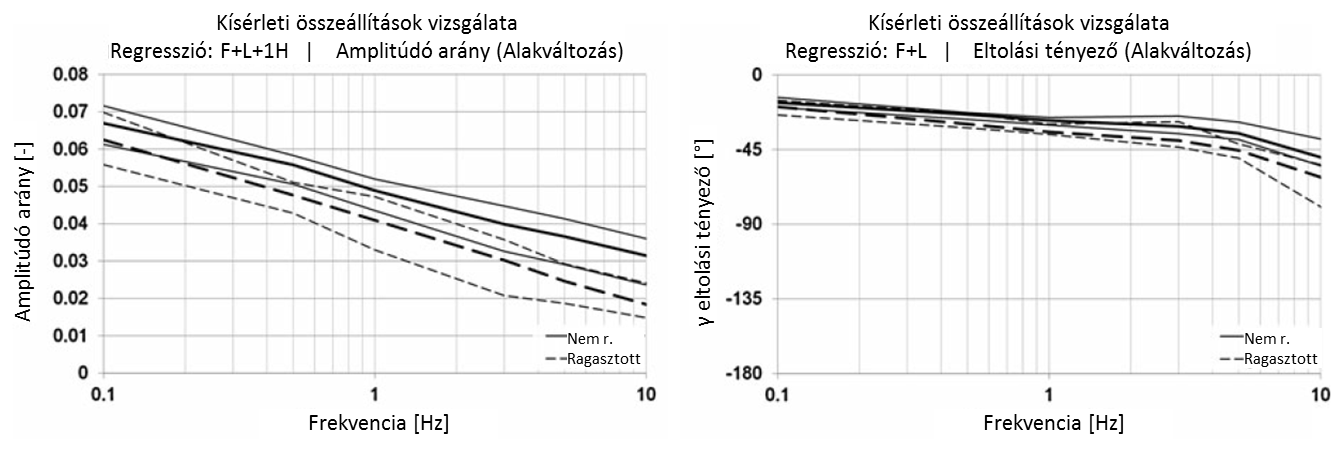
A 10. ábra az AR amplitúdó arányt és a γ eltolási tényezőt mutatja a tengelyirányban elhelyezett elmozdulásmérők jeleinek esetében. Az AR és a vizsgálati frekvencia között egyértelmű kapcsolat figyelhető meg. Minél magasabb a frekvencia, azaz minél dominánsabb a rugalmas viselkedés, annál alacsonyabb az első harmonikus részaránya. A vizsgálatok adatsorai 0,1 Hz környékén kezdődnek, ahol a nem-ragasztott összeállítás esetében az AR értékek 6,2-7,1%, míg a ragasztott esetben 5,5-7,0% közöttiek. A frekvencia növekedésével az arány a ragasztott összeállítás esetében gyorsabban csökken, 10 Hz-nél 1,4-2,4% közötti, míg a nem-ragasztott összeállításnál az amplitúdó arány értéke 10 Hz-nél 2,4-3,6% közötti. A középértékeket tekintve az AR nem-ragasztott esetben 0,1 Hz frekvencián 7%-al, míg 10 Hz-nél már 42%-kal nagyobb a ragasztott összeállításhoz képest. Ez azt is jelenti, hogy a frekvencia növekedésével az első harmonikus hatása csökken, ami összhangban van az egyszerű függvény determinációs együtthatójának 8. ábrán bemutatott adataival.
A függvények illeszkedésének minősége az F+L függvény esetében a frekvencia növekedésével javul. Ez érthető, hiszen magasabb frekvenciákon az első harmonikus dominanciája egyre inkább csökken. A teljes vizsgált frekvencia-tartományt tekintve a ragasztott összeállítás esetén az AR értéke alacsonyabb, ami azt mutatja, hogy a ragasztott próbatestek alakváltozása jobban követi a szinuszos terhelést, mint a nem-ragasztottaké.
A 10. ábra jobb oldala a γ eltolási tényező adatait szemlélteti, mely középértékét tekintve 0,1 Hz-en -17° a nem-ragasztott, míg -19° a ragasztott összeállítás esetén. Ez azt jelzi, hogy a terhelés fázisában a közelítés meredekebben nő, a tehermentesítés fázisában pedig laposabban csökken. 5 Hz vizsgálati frekvenciáig az eltolási tényező értéke -45° fölött marad. Hasonlóképpen, az AR értéke csökken, ami a terhelés és tehermentesítés fázisa közötti egyre csökkenő gradienst jelzi. Amikor a frekvencia 10 Hz, a γ értéke a ragasztott összeállításnál a -60°-ot, a nem-ragasztott összeállítás esetében pedig a -50°-ot is meghaladja. Az egyre csökkenő amplitúdó aránnyal együtt az alakváltozás függvényének torzulása egyre kevésbé domináns.
A fejezetben megmutattuk, hogy a deformáció alakja a magasabb rendű F+L+1H alakú közelítéssel jobban leírható, mint az alap F+L függvény szerinti közelítéssel. Ez különösen alacsony, 3 Hz alatti frekvenciák esetében igaz. A ragasztott esetben kissé jobb közelítés érhető el az alapfüggvénnyel, ezért arra következtethetünk, hogy a ragasztott próbatestek kevéssé zavart szinuszfüggény szerinti deformációval reagálnak a szinuszos terhelésre. E feltevést az első harmonikus és az alaprezgés közötti AR igazolja, mely a ragasztott esetekben szintén magasabb a teljes frekvenciatartományban.
Az anyagjellemzők vizsgálata a lineáris viszkoelasztikus tartományban
Az előzőekben az erő- és elmozdulásmérők jeleinek elemzését mutattuk be. Érdekes kérdés, hogy a vizsgálati elrendezés befolyásolja-e a származtatott jellemzőket, és ha igen, hogyan. Szintén fontos elemezni, összehasonlíthatóak-e a lineáris viszkoelasztikus tartományban elvégzett CCT vizsgálatok alapján számított anyagparaméterek és egy jól megalapozott merevségvizsgálat eredményei.
Ennek megállapítása érdekében – ugyanazon keverékből gyártott négy próbatesten – négypontos hajlítással (4PBB) merevségvizsgálatokat végeztünk el az EN 12697-26:2004 szerint. A 4PBB vizsgálatok eredményeit a diagramokon pontvonallal jelöltük. Az előzőekhez hasonlóan vastag vonal jelzi a vizsgált próbatestek középértékeit, míg a párhuzamos vékony vonalak a 95%-os konfidencia intervallumhoz tartozó értékeket mutatják.
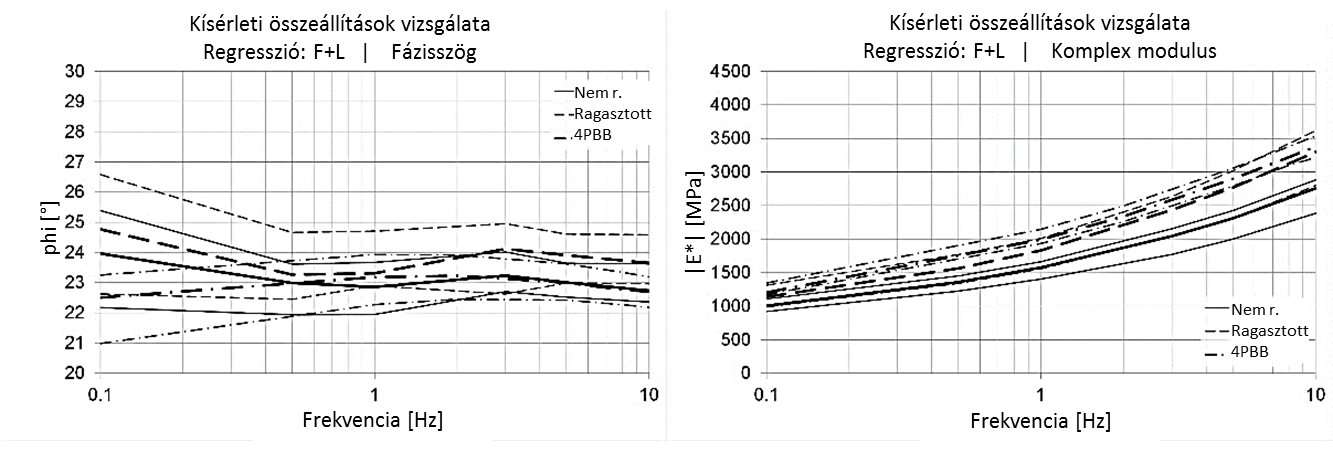
A 11. ábra bal oldala a fázisszöget (φax,ax) mutatja a tengelyirányú terhelés és alakváltozás között az F+L alakú függvény alkalmazása esetén, valamint a 4PBB vizsgálati eredményekből számított φ fázisszöget. A két CCT vizsgálati összeállítás fázisszöge közötti eltérés nem jelentős, értéke a teljes frekvencia-tartományban 1°-nál kisebb. A CCT és 4PBB vizsgálatokból számított fázisszög-különbség maximuma a ragasztott összeállítás esetén 0,1 Hz-nél található. A középértékek között 2,2° eltérés tapasztalható, de a 95%-os konfidencia intervallum határai a két esetben egybevágnak még 0,1 Hz frekvencia esetén is. Következésképpen a különbség elhanyagolhatónak tekinthető.
A 11. ábra jobb oldala az |E*| komplex modulus értékét mutatja mindkét CCT összeállítás, valamint a 4PBB esetében. Az adatok elemzése előtt megjegyzendő, hogy a vizsgált próbatestek térfogatjellemzői lényegesen különböznek. A próbatestek hézagtartalmának középértéke a nem-ragasztott összeállítás esetében 6,0 tf%, míg a ragasztott összeállításnál 4,0 tf% (2. és 4. táblázat). A négypontos hajlítással vizsgált próbatestek hézagtartalma 4,2 tf%, így az eredmények inkább a ragasztott vizsgálatokkal vethetők össze, ugyanis Hofko és Blab kutatásában megmutatta, hogy a komplex modulust tekintve a hézagtartalomnak jelentős hatása van a merevségre (Hofko & Blab, 2012). Ennek mértéke magas (10 Hz) frekvenciák esetén az alacsonyabbakhoz képest (0,1 Hz) mintegy négyszeres. Hasonló arány látható a komplex modulust vizsgálva a CCT vizsgálatok esetében. A ragasztott (magasabb hézagtartalmú) és nem-ragasztott (alacsonyabb hézagtartalmú) összeállítások esetében mért komplex modulusok közötti különbség 0,1 Hz frekvencián 130 MPa, míg 10 Hz-en már 540 MPa.
Jelen és a Hofko és Blab kutatásában (Hofko & Blab, 2012) bemutatott vizsgálatok alapján megállapítható, hogy a modulusok közötti különbség mindkét CCT vizsgálat esetén nagymértékben függ a hézagtartalomtól, ugyanakkor nem függ a vizsgálati összeállítás voltától. A 4PBB eredményeit tekintve megállapítható, hogy a ragasztott CCT vizsgálatokhoz képest értelmezhető eltérés van, melynek maximuma 1 Hz frekvencián 162 MPa (10,4%). A 95%-os konfidencia intervallumot tekintve azonban az eltérések nem jelentősek. Kijelenthető, hogy a CCT vizsgálatokból nyert anyagi paraméterek (merevség és fázisszög) a lineáris viszkoelasztikus tartományban jól összehasonlíthatóak olyan szabványos vizsgálatok eredményeivel, mint a 4PBB.
Összefoglalás
Kétféle CCT vizsgálati elrendezés eredményeinek F+L+1H alakú egyenlet szerinti regresszióját vizsgálva és 4PBB vizsgálati eredményekkel való összehasonlítása alapján az alábbi következtetések vonatóak le:
- az összetett F+L+1H egyenlet szerinti regressziós függvény alkalmas a szinuszos függvények alakjának gyors vizsgálatára. Ha a függvény torzult, az AR amplitúdó arány és a γ shift-faktor segítségével jellemezhető a torzulás
- Az F+L+1H megközelítés értékes adatokat szolgáltathat az oszcilláló vizsgálati adatokról. Segítségével a vizsgálóberendezés vezérlésének meghibásodása és a terhelés függvény torzulásának mértéke könnyen kimutatható és leírható.
- Az erőmérő adatait vizsgálva nem található lényeges torzulás a szinuszos függvényhez képest. Az alap és az összetett regressziós függvénnyel is jó illeszkedés tapasztalható mindként vizsgálati elrendezés esetén, a teljes vizsgált frekvenciatartományban. Az AR amplitúdó arány 10 Hz-ig igen alacsony (<5‰), így a szinuszos terhelésben nem érzékelhető figyelemre méltó torzulás. Mivel a vizsgálatokat erővezérelt módban végeztük, az eredmények a berendezés vezérlőegységének pontos működését mutatják egészen 10 Hz frekvenciáig, a próbatest és a terhelő lemezek közötti kapcsolattól függetlenül.
- Az adatok vizsgálata alapján látható, hogy az elmozdulásmérők jele nem közelíthető olyan jól az alap szinuszfüggvénnyel, mint az erőmérők jele esetén. A ragasztott adatokra jobban illeszkedik az F+L szerinti regresszió. Az összetett függvény szerinti regresszió esetén a korrelációs együttható értéke 0,999 fölötti mindkét vizsgálati elrendezés esetén. Az AR amplitúdó arány vizsgálata alapján megállapítható, hogy különösen alacsonyabb frekvenciák esetén, az alakváltozás torzulása a terhelési fázisban meredekebb, a tehermentesítés fázisában laposabb függvényt eredményez. Ez a torzulás nem-ragasztott vizsgálatnál erősebb.
- A mechanikai anyagparamétereket tekintve, nem találtunk különbséget a két vizsgálati elrendezés között a fázisszögeket vizsgálva. Hasonlóképpen, nem találtunk szignifikáns eltérést a fázisszögek között a CCT és 4PBB vizsgálatokat összehasonlítva sem.
- A komplex modulust vizsgálva a nem-ragasztott vizsgálatok esetében alacsonyabb eredményeket kaptunk, mint ragasztott esetben. Kimutatható, hogy a különbség a próbatestek közötti hézagtartalombeli eltéréssel függ össze, és nem a vizsgálati elrendezésből eredő különbségekkel. Az előzőekhez hasonlóan, szignifikáns eltérések a CCT és a 4PBB eredmények között nem mutathatóak ki.
- Következésképpen kijelenthető, hogy az összenyomódás fázisában végzett vizsgálatok alkalmasak az aszfaltkeverékek anyagi tulajdonságainak leírására a lineáris tartományban a próbatestek és a terhelő lemezek közötti kapcsolattól függetlenül, és a CCT eredmények összehasonlíthatóak a 4PBB eredményekkel.
Hivatkozások
[1] Francken L (1977) Permanent deformation law of bituminous road mixes in repeated triaxial compression. Proceedings of the 4th international conference on structural design of asphalt pavements, Ann Arbor
[2] European Standard EN 12697-25(2005) Bituminous mixtures – Test methods for hot mix asphalt – Part 25: Cyclic compression test
[3] Jaeger W (1980) Mechanical Behavior of Hot Mix Asphalt Specimens (Mechanisches Verhalten von Asphaltprobekörpern). Publication of the Institute of Road and Railway Engineering, University of Karlsruhe, Germany
[4] Weiland N (1986) Deformation Behavior of Hot Mix Asphalt Specimens under repeated loading (Verformungsverhalten von Asphaltprobekörpern unter dynamischer Belastung. Publication of the Institute of Road and Railway Engineering, University of Karlsruhe, Germany
[5] von der Decken S (1997) Triaxial tests with sinusoidal axial and radial loading to investigate the deformation resistance of hot mix asphalt (Triaxialversuch mit schwellendem Axial- und Radialdruck zur Untersuchung des Verformungswiderstandes von Asphalten). Publication of the Institue of Road Engineering, Technical University of Brunswick, Germany
[6] Kappl K (2007) Assessment and modeling of permanent deformation behavior of bituminous mixtures with triaxial cyclic compression tests. Dissertation, Vienna University of Technology, Austria
[7] Hofko B (2011) Towards an enhanced characterization of the behavior of hot mix asphalt under cyclic dynamic compressive loading. Dissertation, Vienna University of Technology, Austria, http://www.ub.tuwien.ac.at/diss/AC07812414.pdf
[8] Di Benedetto H, Partl M, Francken L, De La Roche Saint André C (2001) Stiffness testing for bituminous mixtures. Materials and Structures, 34, 2, p 66-70, Springer Netherlands, 66-70, Doi: 10.1007/BF02481553
[9] European Standard EN 12697-26 (2004) Bituminous mixtures – Test methods for hot mix asphalt – Part 26: Stiffness
[10] Hoeflinger G (2006) Investigation of specimen preparation of hot mix asphalt using the segment roller compactor. Master Thesis, Vienna University of Technology, Austria
[11] Airey G, Rahimzadeh B and Collop A (2003) Viscoelastic Linearity Limits for Bituminous Materials. Proceedings of the 6th International RILEM Symposium on Performance Testing and Evaluation of Bituminous Materials, Zurich, Switzerland
[12] Hofko B and Blab R (2012) Impact of air void content on the viscoelastic behavior of hot mix asphalt. Proceedings of the 3rd Four-point bending beam conference, Davis, CA.
Fordította:
Soós Zoltán
Géber Róbert